袋裝飼料裝車機龍門架有限元分析及優化

■史常青 袁 波 鄧援超* 董 陽

（1.湖北工業大學，湖北武漢430068；2.中科天工（武漢）智能技術有限公司，湖北武漢430200）

近年來，飼料加工業自動化程度不斷提高，飼料裝車自動化裝置一直是現在熱門研發項目的產品之一，隨著袋裝飼料自動化裝車機的不斷完善，技術上的不斷提高，自動裝車機正逐步走向實際應用。袋裝飼料自動化裝車機的結構形式有多種，帶機械手式的袋裝飼料裝車機是目前的主流方向，為了提高效率，將機械手從一個增至多個，而龍門架作為多個機械手的主要支撐物，在碼垛過程中不僅需要承受較大的載荷，而且需要單自由度的移動，這就要求龍門架有足夠的強度和剛度以及適當的質量，所以在龍門架的設計過程中，不僅需要分析結構的強度剛度，保證龍門架具有足夠的強度，還需要通過優化設計，使龍門架充分發揮材料的性能，以節省材料或減輕自重，在滿足產品性能要求的同時滿足工作要求。

1 龍門架模型的有限元分析

1.1 龍門架載荷的確定

裝車機部分結構如圖1所示，龍門架所承受的的載荷主要包括兩個機械手裝置自重、機械手裝置抓取的4 袋袋裝飼料的自重以及龍門架自重，通過Solidworks的質量屬性可得單個機械手自重約770 kg，查閱相關資料可知袋裝飼料通常為40 kg/袋，為了確保龍門架結構的安全性和可靠性，需要在龍門架極限工況的情況下對其進行有限元分析，當兩個機械手裝置帶動4袋袋裝飼料移動至龍門架跨中位置時，龍門架將處于極限工況，即總負載F=17 000 N作用在龍門架兩根橫梁的跨中位置，每根橫梁跨中位置受集中力=8 500 N；龍門架受自重載荷為G，總的受力如圖2所示。

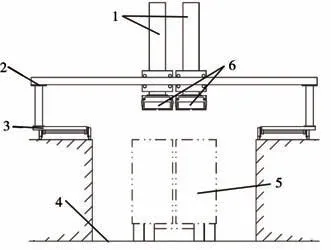
圖1 裝車機部分結構簡圖

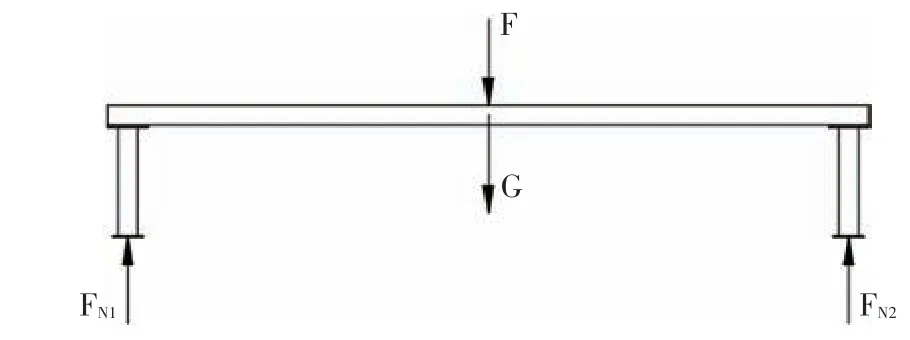
圖2 裝車機龍門架受力圖

如圖2所示可得受力平衡表達式：

1.2 模型描述

龍門架結構如圖3所示，龍門架由四根支撐柱以及兩根橫梁采用螺栓連接組成，其跨度有8.5 m。兩根橫梁均采用鋼板拼焊的方式制作，橫梁截面如圖4所示，每根橫梁組成包括：上、下側板，左、右側板，其中板厚均為9 mm，且由Q235B鋼板切割焊接制成。支撐柱使用材料是Q235冷彎矩形空心型鋼管120 mm×120 mm×8 mm，支撐柱上表面與橫梁通過螺栓連接，下表面與移動機架通過螺栓連接。

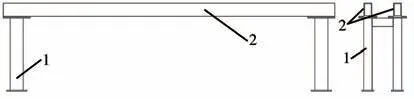
圖3 龍門架結構

1.3 模型簡化

本文采用Solidworks 建立三維模型后導入至Ansys workbench進行有限元分析，龍門架模型有較多的連接孔位，實際情況較為復雜，為了減少計算規模，提高工作效率，在保證計算精度的前提下對其有限元模型進行適當的簡化處理，具體簡化過程如下：

①略去龍門架的連接螺栓和孔位；

②龍門架各零件均采用拼焊的加工方式，根據焊接部位可以近似認為是剛性連接的特性，可以在建立其有限元模型時將焊接的零件建模成一個整體。

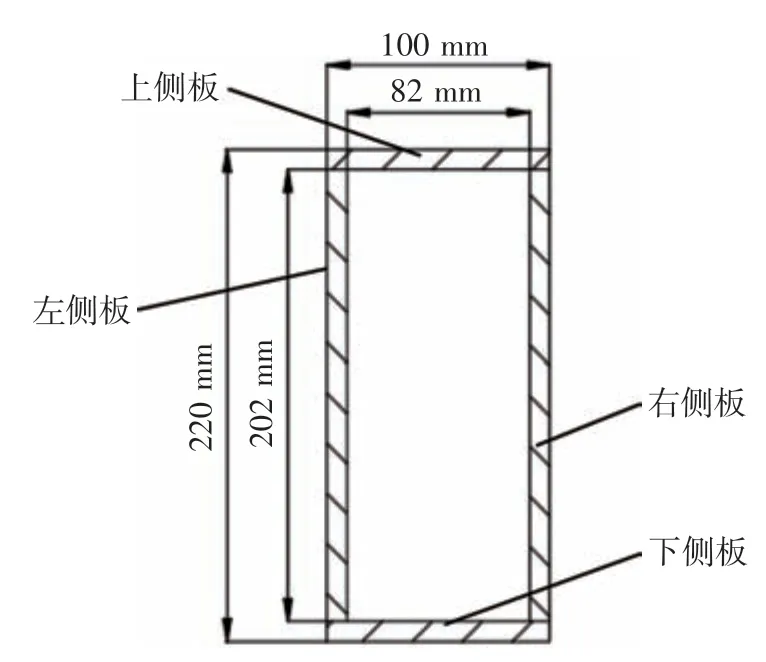
圖4 橫梁截面焊接示意圖

1.4 三維建模

根據上述簡化過程，使用solidworks 建立裝車機龍門架的三維模型如圖5所示。

圖5 裝車機龍門架三維立體模型圖

2 龍門架的有限元分析

2.1 模型前處理

將Ansys workbench 與solidworks 設置關聯后，在solidworks 中建立模型并直接在菜單欄中打開Ansys workbench 進行線性靜力學分析，選擇材料為Q235結構鋼，其材料特性如表1 所示，對龍門架的網格劃分采用六面體劃分網格的方法，六面體單元的計算精度要高于四面體單元，抗變形能力強，且在相同大小的單元條件下，六面體網格劃分的單元數量比四面體網格劃分的單元數要少得多，可以大大提高計算速度，六面體網格單元尺寸設置為20 mm，網格劃分后龍門架共劃分為277 820個節點，60 431個單元。

2.2 施加邊界條件

龍門架的支撐柱下底面通過螺栓與移動機架固定連接，故將支撐柱的四個連接面處施加完全固定的約束條件，使其自由度被完全約束；將橫梁與支撐柱的螺栓連接面處設置為No separation的接觸方式，此接觸方式可以限制接觸面的法向運動，反映出螺栓連接的緊固效果；在兩根橫梁跨中位置各施加集中力F=8 500 N，由于龍門架跨度較大，其自身包括兩組支撐柱和兩根橫梁的重量是不可忽略的，所以在Ansys workbench需選擇Inertial 欄目中Standard Earth Gravity，Ansys workbench給各個單元上施加重力均布載荷。將上述約束與載荷施加到龍門架上，得到其模型示意圖如圖6所示。

表1 材料特性

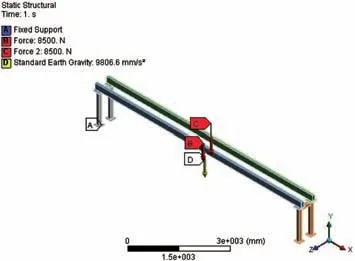
圖6 約束與載荷施加模型示意圖

2.3 初始模型靜力結果與分析

初始設計數據下龍門架的整體應力云圖及變形圖，如圖7所示。

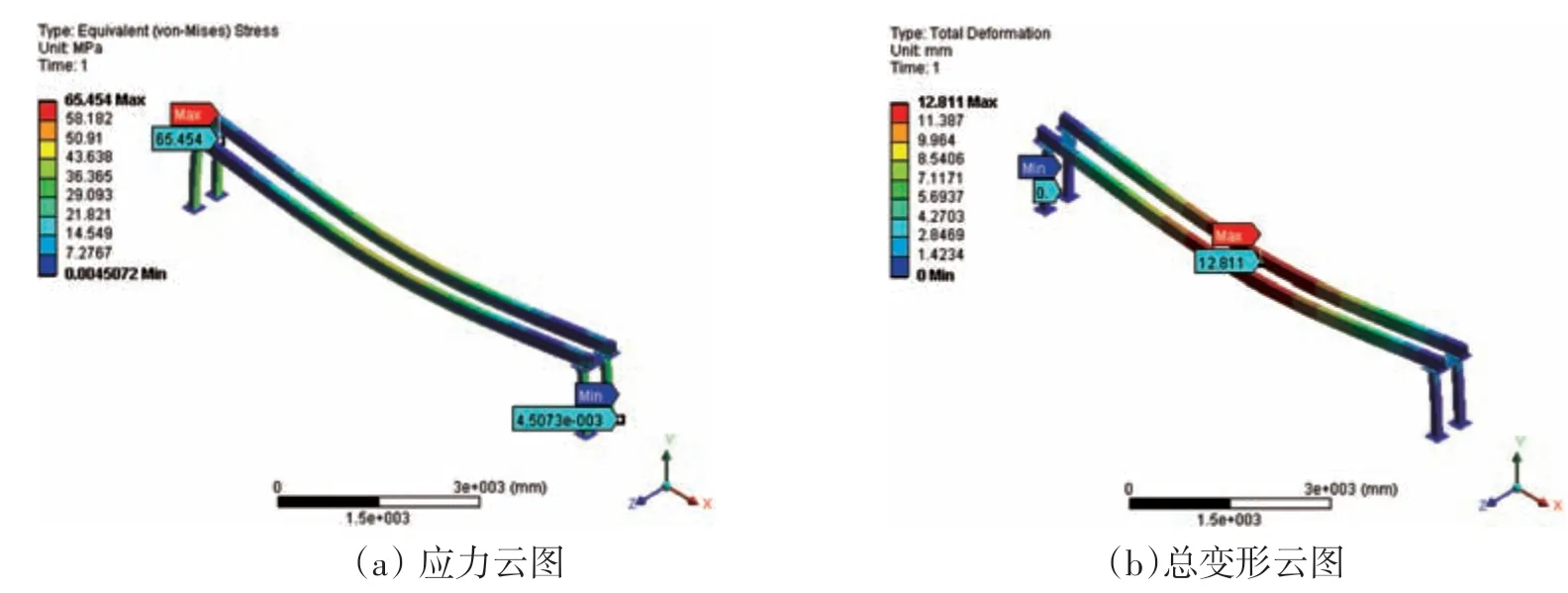
圖7 龍門架靜力學仿真結果

通過有限元靜力學分析，得到裝車機龍門架初始設計結構的最大等效應力為65.454 MPa，最大變形量為12.811 mm，最大等效應力小于許用應力值156 MPa，最大變形量小于允許變形量17 mm，即初始設計參數滿足龍門架的工況要求。但是此初始設計參數下的龍門架質量較高，對驅動裝置的設計要求需要提高，從而使整體設計變得更為復雜，所以需要在滿足使用要求的前提下對龍門架進行進一步優化設計。

3 橫梁尺寸優化數學模型

在優化設計中，需要保證龍門架能夠在最不利的載荷情況下不發生大的變形，同時又要求龍門架的質量盡可能的小。提高機械零部件的抵抗彈性變形能力主要有以下幾個措施：

①減小主要支撐零部件的支撐跨距；

②增大零部件主要抗彎截面的截面尺寸（彎曲截面系數）；

③增加主要支撐零部件的數量等。

由于空間結構限制，本文采取上述方法2對龍門架橫梁截面尺寸進行優化。在上述分析的基礎上，以橫梁截面尺寸為優化變量，以橫梁的質量、龍門架的最大變形量和最大等效應力值為目標函數，在滿足不大于龍門架初始模型最大變形量12.811 mm的條件下，對橫梁截面尺寸進行優化，最大限度的降低橫梁質量。

3.1 設計變量

初始模型截面尺寸如圖4所示，根據慣性矩公式以及抗彎截面系數公式可知矩形截面的H 尺寸對截面的慣性矩和抗彎截面系數影響較大，且在離梁的中性軸較遠處，配置較多的材料，能大大提高材料的利用率，由于龍門架橫梁受力面主要在截面左側，且橫梁右側板朝龍門架外側，無任何連接零件，即在初始模型截面面積S=5 436 mm2一定的情況下，選擇優化以下兩個參數：橫梁高H 和橫梁右側板厚度t右，在減小右側板厚度時，將減少的材料均勻分配至上下板的厚度上，再將過渡截面按比例n 縮放得到優化截面，優化流程如圖8所示。

圖8 橫梁截面優化流程

初始截面尺寸和優化截面尺寸如圖9 和圖10 所示，其中，截面面積均為S，A、A1分別代表初始截面和優化截面的外形尺寸的寬度，H、H1分別代表初始截面和優化截面的外形尺寸的高度，h、h1分別代表初始截面和優化截面的內部尺寸的高度，t左、t左1分別代表初始截面和優化截面的左側壁厚，t右、t右1分別代表初始截面和優化截面的右側壁厚。

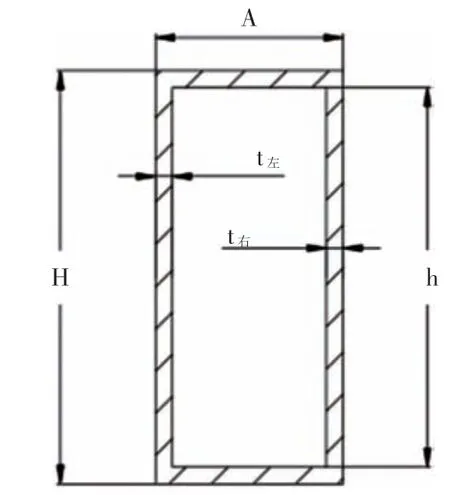
圖9 初始截面尺寸

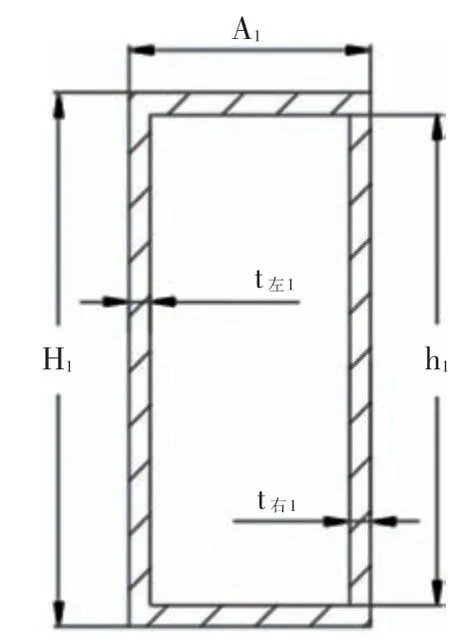
圖10 優化截面尺寸

橫梁截面多目標參數優化設計變量如表2所示，初始截面與優化截面的尺寸關系表達式如下：

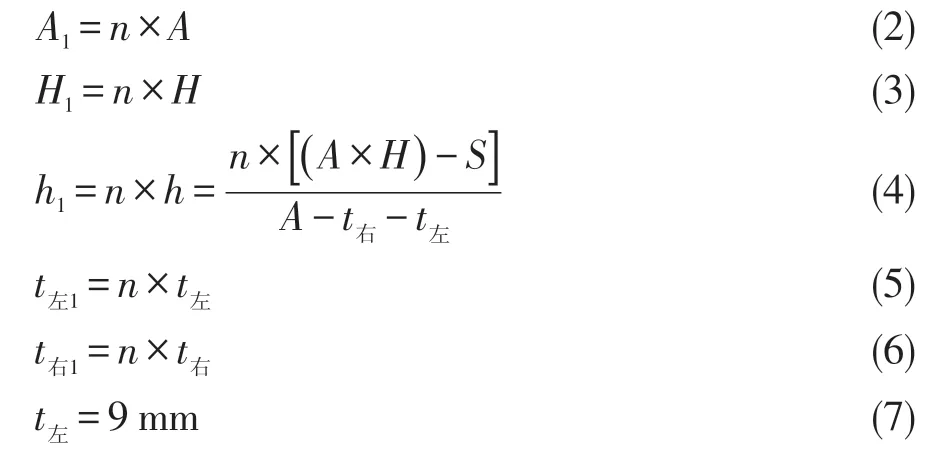
表2 橫梁截面多目標參數優化設計變量

3.2 目標函數

橫梁的橫截面優化的目標是在滿足龍門架自身強度和工作要求的基礎上，實現橫梁的優化減重設計，因此將設計變量的取值范圍、龍門架的最大變形量不大于初始值、橫梁質量最小化以及龍門架最大等效應力小于等效應力許用值作為約束條件和優化目標函數，優化數學模型表達式如下：

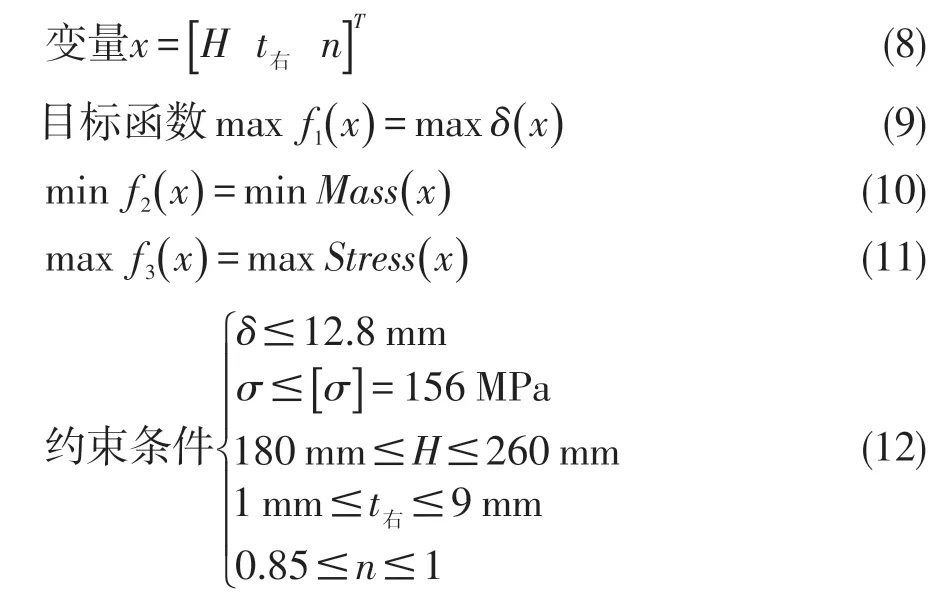
式中：δ——龍門架的最大變形量(mm)；

σ——龍門架的最大等效應力(MPa)。

4 橫梁的多目標參數優化

多目標優化（Multi-objective Optimization）是指在優化問題中，要求的目標指標往往不唯一，且目標之間相互沖突，一個目標的改善有可能導致另一個目標性能的惡化，即需要在多個目標之間進行協調和折中處理，使多項目標函數盡可能達到最優。機械結構的性能大都由多個指標共同決定，并且這些指標之間又相互制約。對于機械結構的性能問題，就需要通過多目標優化的手段進行解決，對于上述的尺寸優化數學模型可以通過soliworks 對橫梁進行參數化建模即可導入到Ansys workbench 中，Ansys workbench 中的實驗設計優化模塊Design Exploration 的優化項目包括直接優化、參數優化、響應面、響應曲面優化和六西格瑪分析，其中的直接優化和響應曲面優化屬于目標驅動優化，本文選用響應曲面優化，響應曲面優化項目包括實驗設計模塊（Design of Experiments）、響應曲面模塊（Response Surface）和優化模塊（Optimization）。

4.1 實驗設計（Design of Experiments）

對多目標進行參數優化設計前，首先需要對設計變量進行實驗設計。實驗設計是運用蒙特卡羅抽樣技術對樣本點采集，經計算后，每組樣本點數據都對應一組響應值（目標函數）。龍門架的實驗設計將表2中的設計變量H、t右、n 作為實驗設計的輸入參數P1、P2、P3，并確定輸入參數的輸入范圍，在靜力學分析模塊中將最大變形量、最大等效應力、橫梁質量設定為實驗設計的輸出參數P4、P5、P6，并采用基于分數因子設計的中心合成設計法（CCD 法）自動生成求解出15組樣本設計點，樣本設計點數據如表3所示。

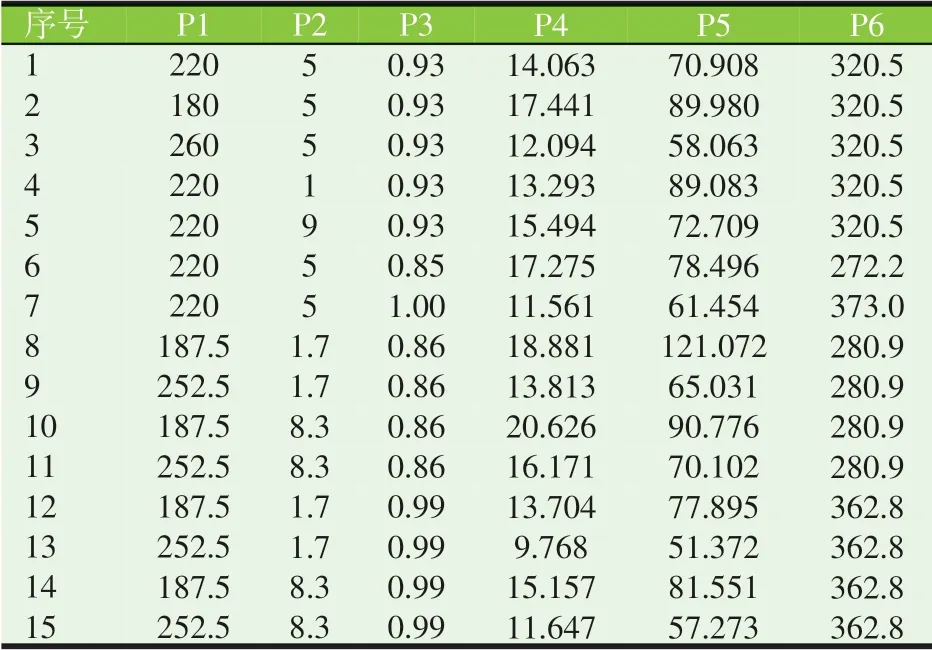
表3 自動生成求解的15組樣本點及響應值

4.2 響應曲面（Response Surface）

響應曲面是利用實驗設計的樣本點，通過基于數理統計方法的響應曲面技術擬合出輸入參數與某一響應值之間的函數關系，利用圖像處理技術獲得的曲面（線）圖。這種方法能夠相當直觀的顯示出設計變量和響應值之間的函數關系，其簡化的表達式為：

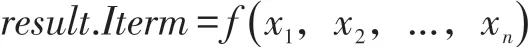
式中：result.Iterm——輸出變量；

x1，x2，...，xn——輸入變量。

通過實驗設計得到了設計變量橫梁高H和橫梁右側板厚度t右對最大變形量和最大等效應力的三維響應曲面，設計變量縮放比例n對橫梁質量的二維響應曲線，響應曲面如圖11所示，響應曲線如圖12所示。

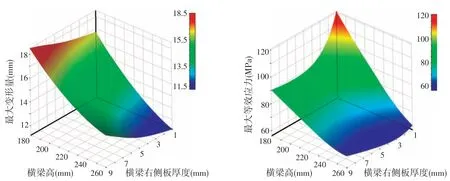
圖11 設計變量H、t 右對最大變形量、最大等效應力的影響

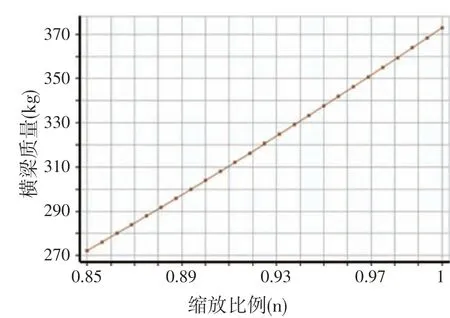
圖12 設計變量n對單根橫梁質量的影響

通過響應曲面擬合能夠看出目標函數（橫梁質量、龍門架最大變形量和最大等效應力值）與設計變量（橫梁高H、橫梁右側板厚度t右和縮放比例n）之間的函數關系。如圖11 所示，在H 趨近于260 mm，t右趨近于1 mm時，龍門架的最大變形量趨近于最小值；在H趨近于260 mm，t右趨近于3.3 mm時，龍門架的最大等效應力值趨近于最小值，如圖12所示，縮放比例n對橫梁質量的響應曲線呈線性遞增關系，n值越小則橫梁質量越小。擬合的響應曲面很直觀的表現出目標函數隨設計變量改變的變化趨勢，為后續的優化提供支持。

4.3 優化設計

目標驅動優化方法是一種多約束、多目標的優化方法，其具有兩種優化算法：篩選法（Screening）和多目標遺傳算法（MOGA）。其中篩選法是采用了一種基于采樣和排序的簡單算法，其支持多目標和約束，以及所有類型的輸入參數，并且具有高效率等優點。多目標遺傳算法全局搜索能力強，能夠在較大解空間中尋求全局最優解等優點。本文選用多目標遺傳算法對龍門架橫梁優化的數學模型進行計算。將橫梁質量最小值目標和最大變形量不大于12.8 mm 約束定義后，通過多目標遺傳算法，從多目標優化的的可行解中求解出三項最優候選設計點，候選點的輸入變量和輸出參數結果如表4所示。

通過橫梁多目標參數優化分析求解產生的最優候選設計點結果，候選點1已經達到了三個目標函數的最優狀態。該候選點的龍門架最大變形量基本與初始模型的龍門架最大變形量相同，龍門架最大等效應力值小于初始模型的龍門架最大等效應力值，均小于許用應力值，龍門架橫梁的質量也減輕了很多，故候選點1可以作為該多目標參數優化的最優解。

表4 候選點結果

4.4 優化結果驗證與對比

將優化設計中的候選點1 的尺寸定義至有限元模型中，在前處理設定與初始模型前處理設定相同的條件下，對新建立的龍門架模型進行靜力學分析，分析結果如圖13 所示，尺寸優化后的龍門架的實際求解最大變形量12.774 mm與候選點1計算出的最大變形量12.799 mm誤差0.025 mm，實際求解最大等效應力值63.629 MPa 與候選點1 計算出的最大等效應力值63.720 MPa誤差0.091 MPa。將橫梁優化后的龍門架與優化前的各靜力學分析數據進行對比，對比結果如表5所示，優化后的橫梁截面如圖14所示。

表5 橫梁優化前后龍門架各靜力學分析數據

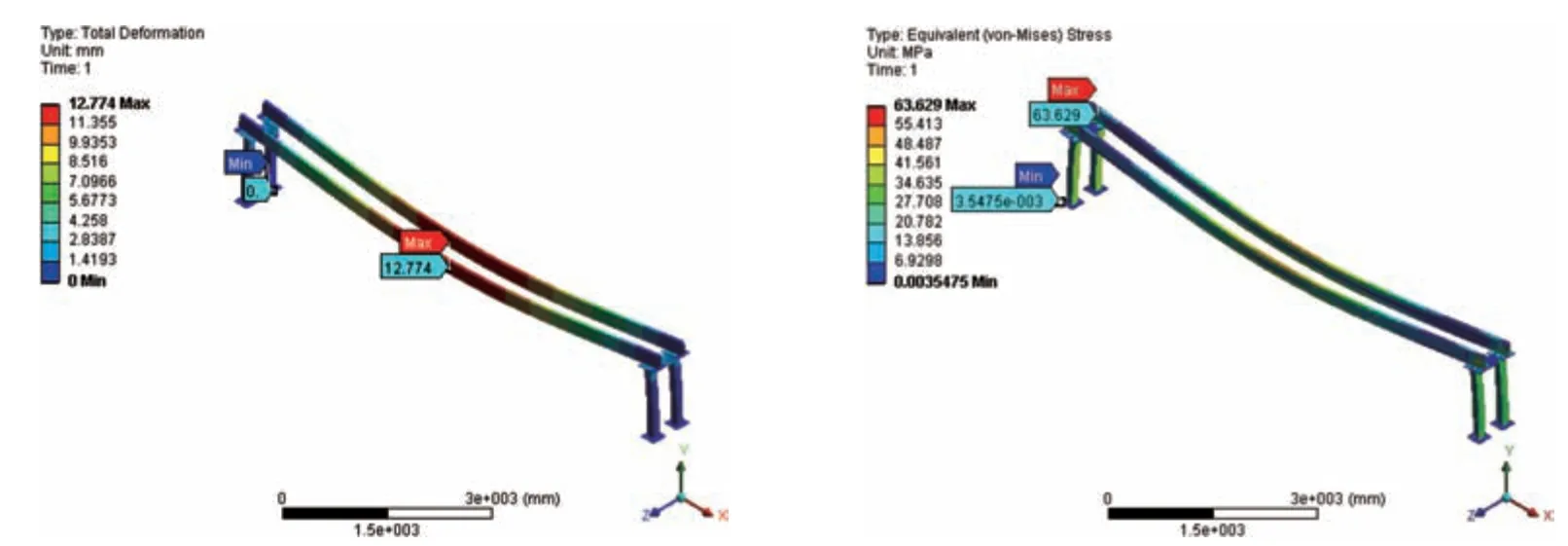
圖13 尺寸優化后龍門架總變形云圖和等效應力云圖

圖14 候選點1截面示意圖

5 結論

本文以袋裝飼料裝車機龍門架為研究對象，進行了靜力學分析，得到了龍門架初始模型的總變形云圖、等效應力云圖。通過實驗設計、響應曲面法、多目標遺傳算法對龍門架橫梁進行了參數優化，橫梁截面優化后的龍門架最大變形量12.774 mm 在不大于初始龍門架龍門架最大變形量12.811 mm的條件下，龍門架橫梁的質量從373.0 kg 減少至295.4 kg，減輕了20.8%，龍門架最大等效應力值從65.454 MPa 減少至63.629 MPa，降低了2.7%，均小于許用應力156 MPa，達到了優化的目的，該優化過程及方法對龍門架的進一步優化具有重要的指導作用。