多無人機對組網雷達系統的協同干擾*

張 哲,吳 劍

(南昌航空大學, 南昌 330063)

0 引言

在現代電子對抗中,組網雷達系統具有較強的抗干擾能力,其軍事作戰應用廣泛。欺騙干擾是一種常用的干擾方式,如何對組網雷達實施行之有效的干擾,是當今電子對抗界面臨的一個重大問題[1]。

文獻[2]提出了一種基于最小識別概率的虛假航跡優化方法,文獻[3]研究了飛行器協同控制問題,利用了最優控制算法對航跡進行了仿真,有一定的可行性。文獻[4-10]對假目標和飛行器間運動模型的參數進行了優化,但協同干擾方面并未詳細研究。文獻[11]重點分析了組網雷達系統的發展現狀以及相關技術,提出了實現干擾所需要解決的問題。文獻[12]利用多變量間的耦合關系和勒讓德偽譜法對單機欺騙單部雷達的模型求解,由于耦合變量間關系復雜,運動參數較多使得模型求解存在較大誤差,在實際應用中較難實現。

文中在進行合理的假設分析后,提出了一種多無人機對組網雷達協同干擾的技術,利用無人機、雷達與假目標三者位置的幾何關系,建立了多機協同飛行的運動模型。給定任意一條虛假航跡,結合PSO算法求解得到綜合考慮無人機數量、航跡坐標以及運動參數的最佳方案,完成航跡欺騙的同時也滿足了飛行速度約束,具有一定參考價值。

1 多機協同干擾的航跡優化模型

1.1 航跡欺騙原理

在多無人機協同飛行的過程中,無人機搭載的干擾設備對接收到的雷達信號處理后轉發回對應雷達,組網雷達信息融合中心將干擾信號形成航跡點信息,基于一定的融合規則,得到多部雷達在統一坐標系下同一空間位置的多個目標航跡點,最終形成了目標的虛假航跡如圖1。通過協同控制無人機的飛行航跡,可在敵方的組網雷達系統中形成一條或多條欺騙干擾航跡,迫使敵方加強空情處置,達到欺騙的目的。

圖1 多機協同干擾組網雷達示意圖

1.2 數學模型

1.2.1 模型準備

多架無人機對組網雷達系統的干擾問題,可先討論單架無人機對雷達的干擾。由于組網內每部雷達的監測距離受限,即通常判斷在某個時刻,若虛假目標信號能夠同時被3部或3部以上的雷達監測,雷達組網系統則認為其為真實目標。通過不同時刻,檢測到連續的合理目標點,構成一條虛假航跡。在定高飛行模式下,由電磁波傳播特性,無人機、假目標和雷達三者相對位置在一條直線上，如圖2所示。

圖2 雷達、無人機和假目標位置關系

在無人機飛行過程中,必然會受到外界環境和自身內部因素的影響。為了完成協同干擾,在建模之前做如下假設:1)無人機在空間區域做直線運動,給定初始航向、航速和飛行高度;2)無人機飛行時視為一個質點,不會受到天氣、導彈攻擊等因素的干擾且不考慮轉彎、爬升和俯沖等；3)不考慮無人機產生的真實目標回波,每隔一定時間獲取一批目標的空間狀態數據。

1.2.2 單架無人機與假目標的運動模型

由圖2知,在空間區域中,A表示雷達,B表示無人機,C表示假目標。假設假目標位置坐標為(xc,yc,zc),無人機坐標為(xb,yb,zb),雷達坐標為(xa,ya,za),s表示時刻,β為初始航向角,v為無人機飛行速度,r為兩者之間的徑向距離,θ為俯仰角,φ為方位角。由于高度h恒定,因此給出二維平面內雷達、無人機和假目標的位置關系表達式,通過幾何關系,在直角坐標系下建立單架無人機與假目標的運動模型為:

(1)

(2)

(3)

由于模型假設飛行高度h恒定,即α=0,得到定高飛行下無人機與假目標的運動模型為:

(4)

為了更直觀的反應雷達、無人機與假目標三者之間的運動關系,現將直角坐標系下的位置關系轉化為以雷達位置坐標為原點的球面坐標系下的方程為:

xs=Rs·cosθ·cosφ
ys=Rs·cosθ·sinφ
zs=Rs·sinθ

(5)

進而對(5)式求導,得到:

(6)

將式(4)代入式(6),改寫成矩陣形式,可得單架無人機與假目標在以雷達坐標為原點的球面坐標系下的運動方程:

(7)

聯立式(4)、式(6)、式(7),得到:

(8)

將式(5)代入式(8),化簡后解得運動參數:

1.2.3 多無人機協同干擾的運動模型

基于單架無人機與假目標運動模型,進一步研究多無人機協同飛行下的運動。

將n個雷達坐標與S時刻的虛假坐標相連,在平面內會產生n·S條直線,確定平面z=h與n·S的交點,即無人機可能出現的位置坐標。在研究多機協同運動時,每架無人機在平面上的位置如圖3。

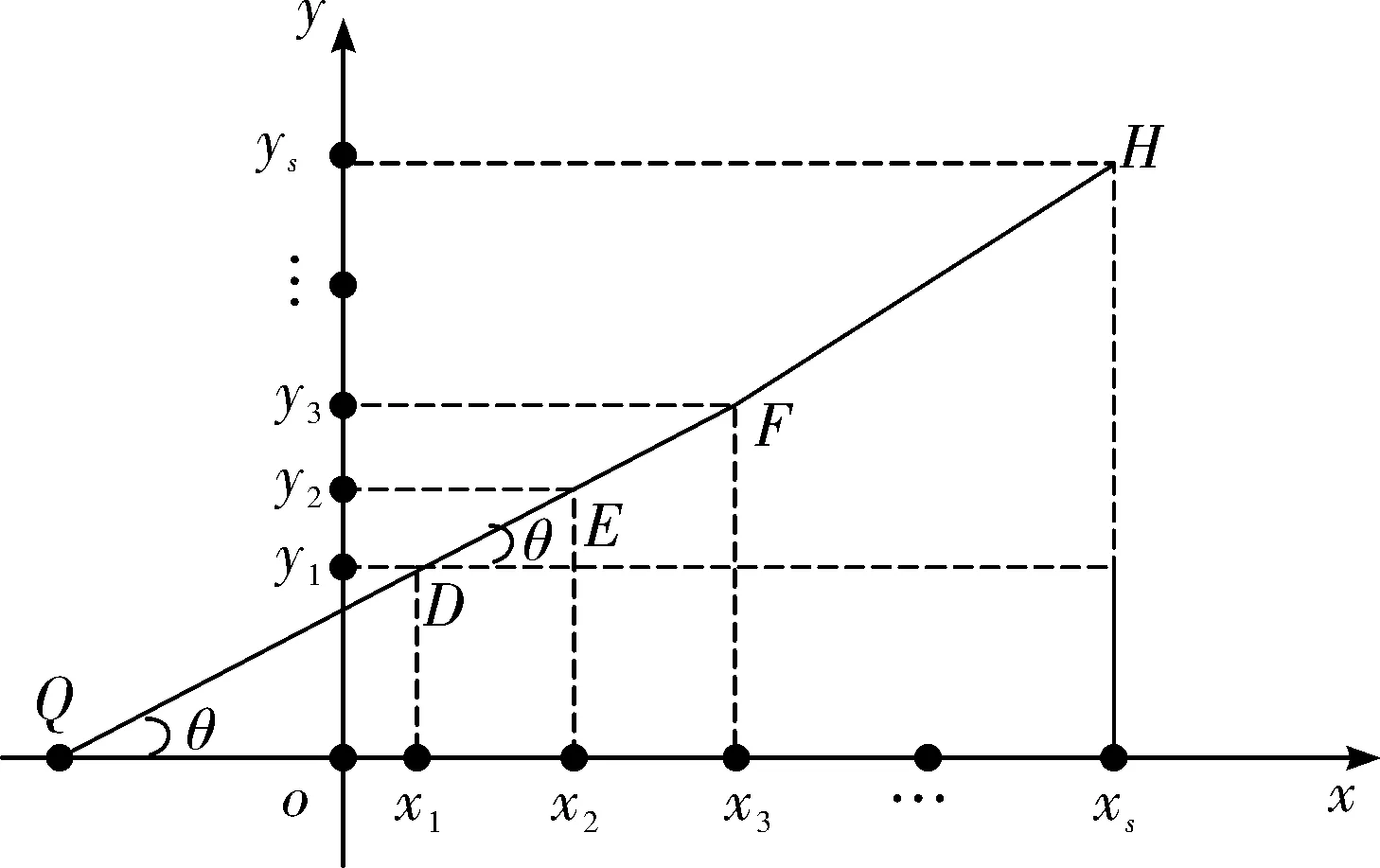
圖3 xoy面無人機位置的時刻坐標

由于無人機做直線運動,將速度vs分解為水平方向vx和豎直方向vy,即

(10)

現每隔△t時間間隔從空間中獲取一批目標的空間狀態數據,對應的第2個時刻的無人機的位置坐標為:

(11)

在第3個時刻,無人機的位置坐標為:

(12)

同理,根據上述方法,可以計算得到在第S時刻,無人機的位置坐標為：

(13)

當多架無人機在一個擁有n部雷達的組網雷達系統干擾下飛行時,在以每部雷達坐標為原點的球面坐標系下,結合無人機與假目標的運動方程,在虛假航跡給定時,便可分別求得任一時刻無人機和假目標的位置坐標,進而能夠更準確地分析無人機的運動狀態,研究多機協同飛行干擾策略。

2 模型求解

2.1 約束條件

無人機與假目標在運動過程中,其速度應受到一定約束:vmin≤vs≤vmax,這里取vmin=120 km/h,vmax=180 km/h。由于是定高飛行模式,高度一般在2 000～2 500 m,這里取h=2 300 m。

2.2 粒子群算法

粒子群算法(PSO)是利用群體中的個體對信息的共享使整個群體的運動在問題求解空間中獲得最優解。組網雷達系統每隔△t時間間隔從空間羅列出平面n·S的交點,即無人機可能出現的位置坐標如圖4所示。根據上節所建立的運動模型求解出任意時刻無人機的運動狀態,由速度約束條件,算出點與點之間可能的路線,即無人機可行路線。

圖4 空中無人機的運動

2.3 求解步驟

假設i表示假目標的初始位置,j表示假目標經過路徑中任意一點位置,設n部雷達同時作用假目標,由于假目標、無人機和雷達三者在同一直線,即雷達與假目標間有n條線段,無人機飛行高度h已定,與這些線段將產生n2個交點,若假目標可飛向另外的(S-1)個目標點,則產生n2·(S-1)條可行路徑。同理,用Mij表示可行線,則S個目標點一共可以產生n2·S·(S-1)/2條可行線。具體求解步驟如下:

step1輸入組網雷達系統中n部雷達的坐標(xam,yam,zam),其中m=1,2, ...,n。固定無人機飛行高度h。

step2求得z=h所在平面與假目標、n部雷達連線的交點,即無人機可能的飛行區域。

step3由模型中無人機速度的約束,即vmin≤vs≤vmax,根據r=v·△t判斷兩點之間是否為可行線。

step4若兩點之間為可行線,則Mij+1,挑選并記錄下該條飛行路線；否則剔除該條路線,保持Mij不變,重復step3。判斷下一目標點。

step5遍歷S個時刻內所有的目標點,生成所有的可飛行路線,并進行分配路線,由運動模型以及坐標公式求解位置坐標。

3 仿真分析

已知組網雷達系統中共有5部雷達,位置坐標分別為雷達1 (80,0,0),雷達2 (30,60,0),雷達3 (55,110,0),雷達4 (105,110,0),雷達5 (130,60,0),單位為km。組網雷達監測區域如圖5。無人機飛行高度為2 300 m,利用首點迭代法[13]產生一條虛假航跡如圖6。取△t為10 s,S=20 s,即飛行時間為200 s,假目標初始位置坐標為(60 600,69 982,7 995),單位：m。

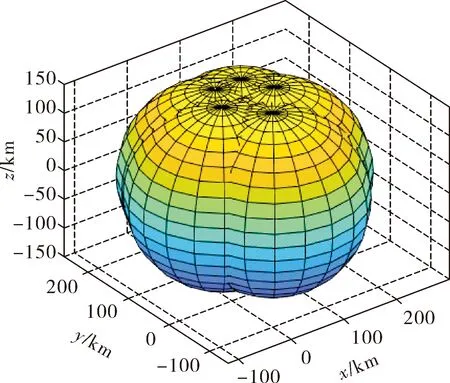
圖5 組網雷達掃描區域

根據無人機與假目標的運動模型,基于PSO算法結合上述求解步驟可算出多無人機對組網雷達協同干擾下的航跡生成如圖7,進而解得至少需要17架無人機協同飛行才能實現所產生的虛假航跡,分別對17架無人機編號,限于篇幅有限,只給出了每架無人機起點和終點的位置坐標如表1。由式(4)、式(5)以及每架無人機的位置坐標,解出無人機與假目標的速度如圖8和圖9。

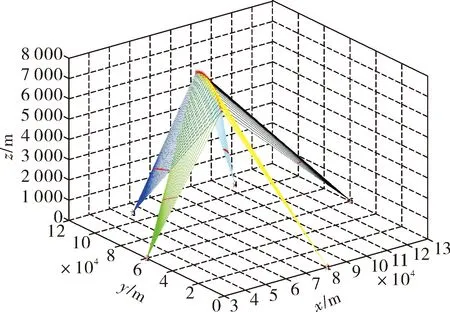
圖7 無人機航跡生成圖

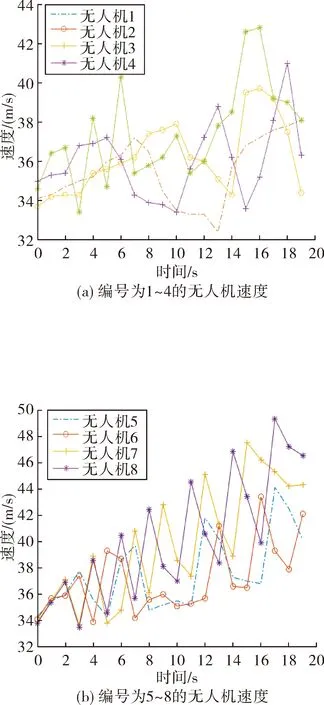
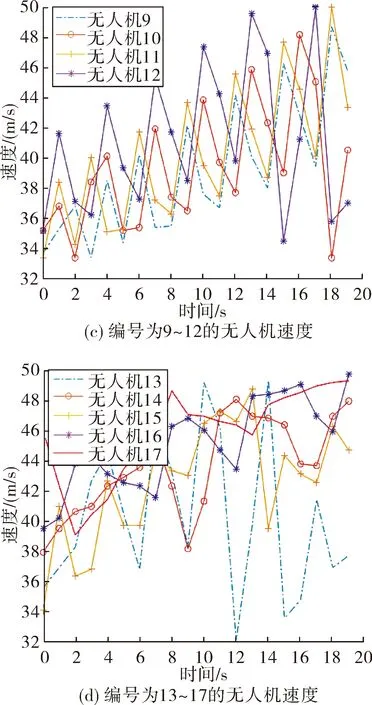
圖8 無人機飛行速度

表1 每架無人機的位置坐標

圖9 假目標的運動速度

4 結束語

多無人機對組網雷達系統的協同干擾是一種十分有效的航跡欺騙方法。文中針對前人研究中的模型參數求解過程復雜,協同飛行效果不佳和不滿足約束條件等問題,建立一種多無人機協同干擾的航跡優化模型,結合PSO算法求解得到綜合考慮無人機數量、航跡坐標以及運動參數下的最佳協同方案,滿足速度約束的同時優化了航跡,對實際應用具有參考價值。