擴展多約束最優制導律特性及其應用*
馬婷婷,刁兆師,魏鈺良,何 婷
(1 北京控制工程研究所,北京 100190;2 中國兵器工業導航與控制技術研究所, 北京 100094)
0 引言
隨著現代化作戰任務變化和精確制導彈藥技術快速發展,為更好地發揮戰斗部威力,針對多約束制導律的研究具有很大實際工程價值。
針對不同應用對象,根據多種理論方法提出了多種帶終端角度約束的制導律[1]。迄今研究較為深入、應用較為廣泛的是基于最優控制依據不同期望指標獲得不同形式的帶多約束制導律。帶終端角度約束制導相關理論成果于1969年在Apollo飛船月球表面垂直著陸得到應用[2],Kim和Grider于1973年較早地提出帶落角約束最優制導律問題[3],自此開始該課題一直吸引著專家學者的關注,并取得許多成果。Zarchan[3]應用施瓦茨(Schwarz)不等式詳細地推導了彈道成型制導律,并解析分析了角度約束和確定性誤差干擾對過載指令的影響。Ben-Asher等[4]研究表明彈道成型制導律有利于降低對剩余時間估計偏差的敏感度。Ryoo等[5-6]后續研究了考慮動力學滯后的制導系統特性以及剩余飛行時間估計問題。常超、祁載康等[7]研究了系統滯后及階次對位置脫靶量和角度脫靶量的影響。Ohlmeyer等[8]以剩余飛行時間冪函數的倒數為最優目標罰函數的權重,最早推導了廣義矢量最優制導律,推廣了傳統彈道成型制導律。劉大衛等[9]采用施瓦茨不等式推導了廣義彈道成型制導律,研究了一階動力學滯后系統的位置和角度脫靶量特性,并給出可用過載限制的導引系數設計方法。王輝等[10-11]求解得到了由初始位置誤差、方向誤差、目標機動及角度約束引起的加速度指令解析解,研究了一階動力學滯后制導系統的無量綱位置脫靶量和角度脫靶量特性。溫求遒等[12]基于線性二次最優控制推導了擴展多約束制導律;通過無量綱化加速度指令變化規律分析,提出了制導初始條件設計方法及最大需用過載估計方法。張文淵等[13]推導了含一階動力學滯后的多約束最優制導律,研究了導引頭隔離度和制導參數對穩定性及制導性能的影響。
在上述文獻基礎上,文中進一步深入研究了擴展多約束制導律的無量綱化加速度指令特性,同時推導了相應視線角變化的解析解并分析了無量綱化視線角變化特性。最后仿真驗證了相關解析結論的有效性。
1 擴展多約束最優制導律
將導彈控制系統視為理想環節,在小角度假設下導彈-目標相對運動幾何關系的簡化線性模型如圖1所示[2],其中:at是目標常值機動加速度,ac是導彈加速度指令。
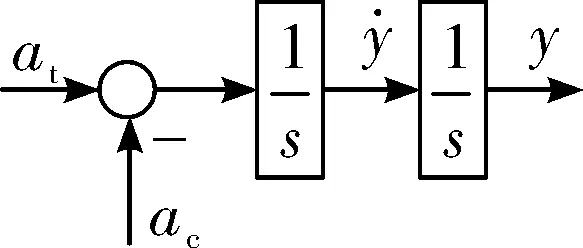
圖1 制導律簡化模型
將圖1模型寫成狀態方程形式為
(1)
帶終端落角約束問題可轉化為終端約束最優控制問題[2],其最優目標罰函數為:
(2)
對應終端約束條件為:
其中,R(t)為正定時變權函數,其定義為:
(3)
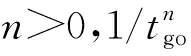
(4)
式中:Np=2(n+2),Nλ=(n+1)(n+2),Nt=(n+2)(1-n)/2。經典比例制導律經驗導引系數Np取值為3~6,且最優控制器往往增益太高、帶寬過高,引起系統失穩[14],因此對應n有效取值范圍為n∈[0,1]。表1給出了3組典型導引系數。
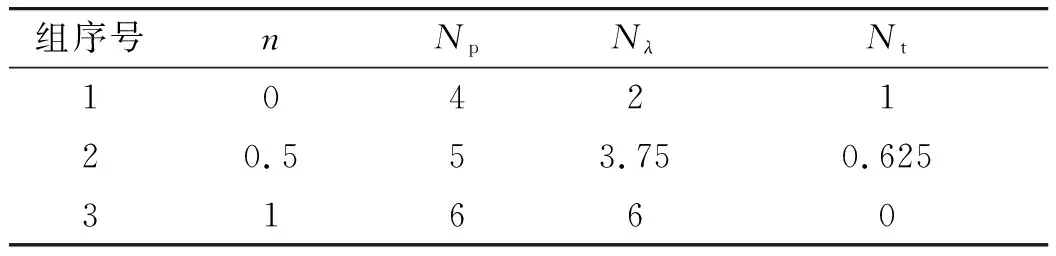
表1 擴展多約束最優制導律典型導引系數
2 最優制導律特性分析
掌握不同確定性誤差及約束因素下的彈道解析特性,尤其是需用過載和視線角變化趨勢,將非常有助于總體方案設計和指標論證,其確定性誤差包括初始位置誤差、初始瞄準方向誤差、目標機動3項,約束是指終端落角約束。
2.1 加速度指令變化
按照文獻[2,10]中最優制導律的解析加速度指令表達式為:
(5)
令導彈初始瞄準方向角誤差為β0,小角度假設下有:
(6)
根據視線角幾何關系有λ=y/r=y/(vctgo),對該式求導得:
(7)
進一步整理得:
(8)
因此可知加速度指令式(5)右側各項為誤差擾動或約束的所需加速度分量,即
ac(t)=a(t)|y(0)+a(t)|β0+a(t)|λf+a(t)|at
(9)
(10)
(11)
(12)
(13)
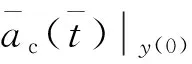
(14)
(15)
(16)
(17)
另外,由圖2知對于n不同取值,無量綱化加速度曲線相交于t1(0.2tf附近)和t2(0.8tf附近)。初始位置誤差、瞄準誤差以及終端落角約束的無量綱化加速度變化趨勢隨n變化一致,當t
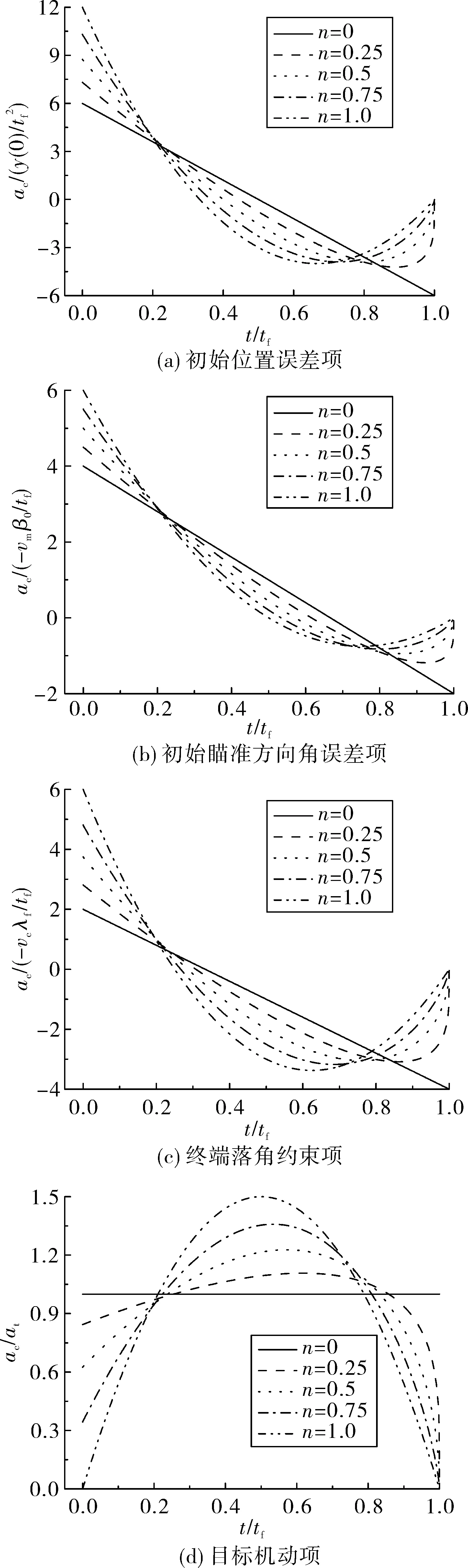
圖2 無量綱加速度變化趨勢
2.2 視線角變化
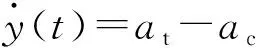
(18)
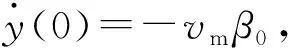
(19)
(20)
(21)
對式(19)~式(22)再次積分可得:
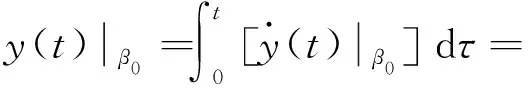
(24)
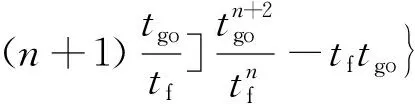
(25)
(26)
由各項引起的視線角變化表達式分別為:
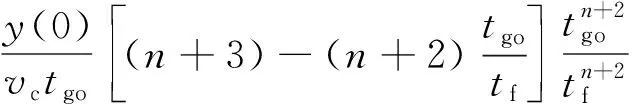
(27)
(28)
(29)
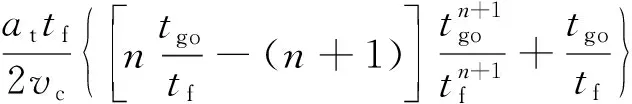
(30)
(31)
(32)
(33)
(34)
(35)
(36)
(37)
(38)
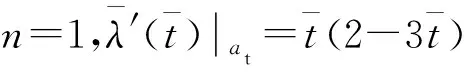
另外,由圖3看出,對于初始位置誤差、瞄準誤差引起的無量綱化視線角變化趨勢一致,隨著n增大,曲線上拉,更快趨于0;終端落角約束引起的無量綱化視線角曲線隨著n增大而下拉,更快趨于1;而目標機動引起的無量綱化視線角曲線隨著n增大而下拉,放慢趨于0。
圖3中無量綱化視線角均大于零,說明4個因素的極性將直接影響視線角變化趨勢。若瞄準角誤差β0與終端期望落角λf極性相反,前者引起的視線角變化趨勢與后者的變化趨勢一致,有利于彈道成型。因此,中制導方案設計最好要保證在轉到多約束制導律時瞄準角誤差β0與終端期望落角λf極性相反。若目標機動at與終端期望落角λf極性相同,前者引起的視線角變化趨勢與后者的變化趨勢一致,有利于彈道成型。
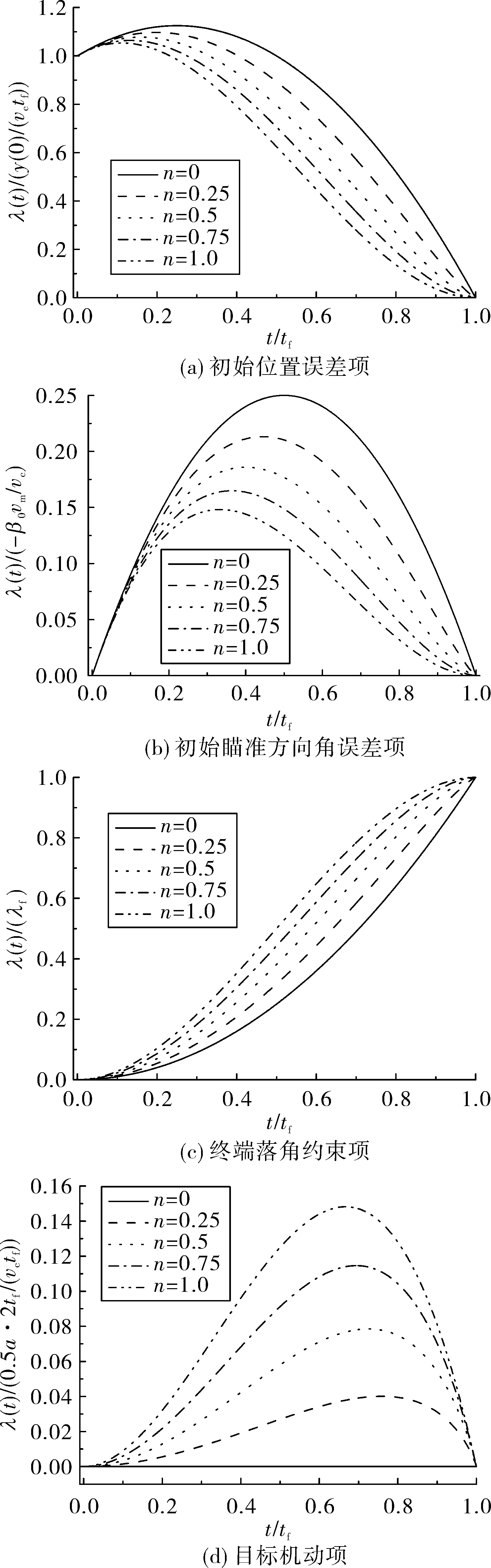
圖3 無量綱視線角變化趨勢
3 工程化應用準則
對于戰術導彈末制導階段,導彈-靜止目標相對運動幾何關系如圖4。圖中,r、λ、θ分別表示彈目相對距離、視線角、彈道傾角。對于打擊靜止目標,終端視線角λf=θf[15]。則視線角變化量為λ*f=λf-λ0,初始瞄準方向角誤差量為β0=θ0-λ0。
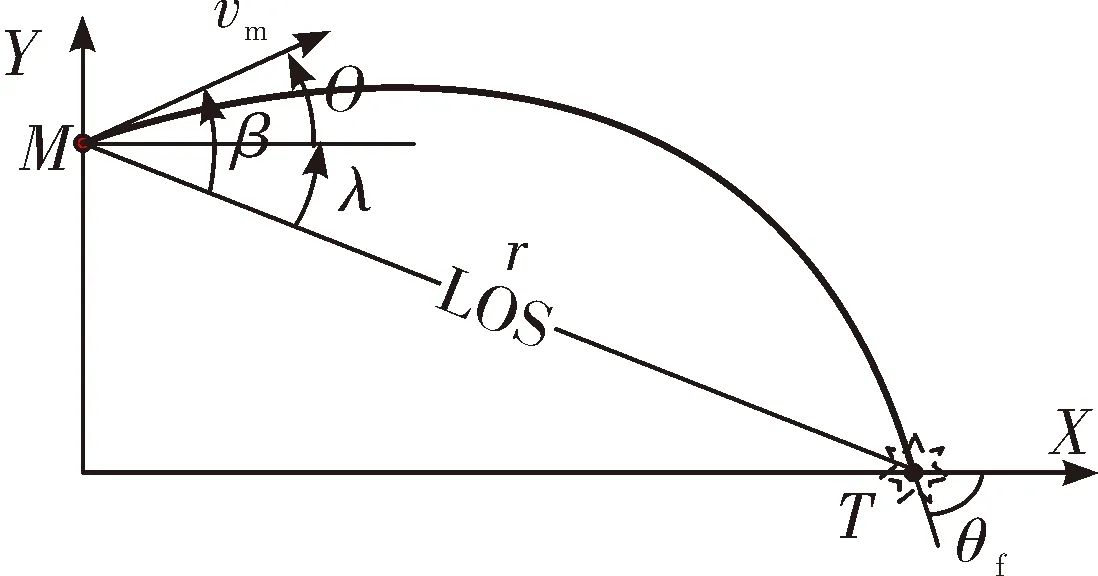
圖4 彈目相對運動幾何關系
由式(9)~式(13)、無量綱化加速度因子和y(0)=0得:
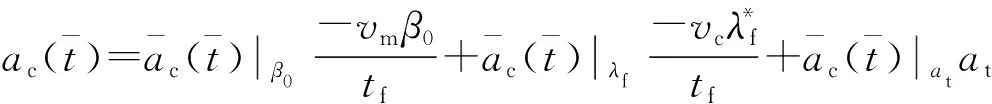
(39)
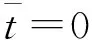
(40)
式中:at是由作用在導彈上的重力等效而來[2],其大小為at=gcosθ,飛行時間tf可由r/vc近似估計。
令導彈可用過載為ap,啟動時刻需要滿足
(41)
(42)
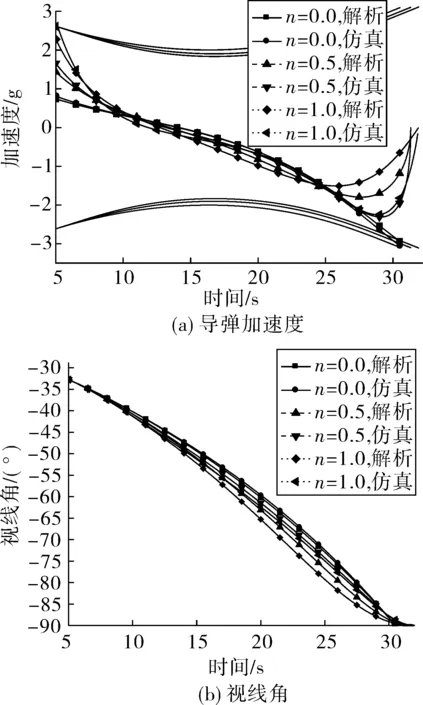
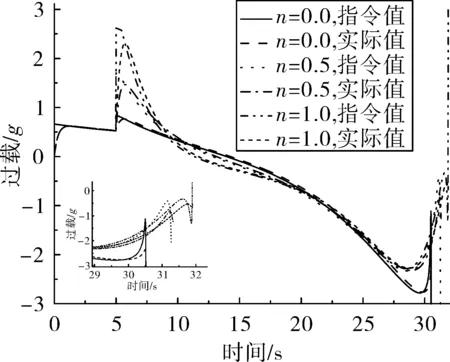
經過分析可得,當0 (43) 考慮控制系統動力學滯后,為保證位置脫靶量和終端角度要求,飛行時間tf應大于控制系統響應時間的15~16倍[10,12],即tf≥(15~16)Tm,可轉化為彈目距離 r0≥vctf (44) (45) 以下3個要素可作為末制導設計的參考準則: ①適當的中制導來保證瞄準方向角誤差和視線角變化量控制在一定范圍內,保證式(41)、式(45)成立; ②選取適當大的制導時間tf滿足式(44),并保證式(41)、式(45)成立,可用過載留有一定裕量; ③若期望終端加速度收斂于零,選取導引系數n>0;同時,導引系數n保證式(41)、 式(45)成立。 以航空制導彈藥縱向平面運動為例進行數學仿真,驗證上述設計原則的有效性,該彈藥無動力,經過穩定、適當中制導進入末制導段完成垂直攻擊任務,初始條件及終端約束要求為:初始高度為Hm=3 km、初始速度vm=300 m/s、彈目水平距離x=6 km、水平投彈θm=0°、期望落角θf=-90°。 取表1擴展多約束最優制導律典型導引系數來進行數學仿真,其結果見表2,彈道曲線如圖5。由表2知,上述典型導引系數均可達到期望脫靶量和期望落角要求,且終端速度散布很小,說明n在[0,1]上取值對終端速度影響不大;當n=0.5、n=1.0時,終端過載接近為零,與解析結論一致,有利于終端攻角收斂,避免大攻角“跳彈”發生。 另外,由圖6(a)知:解析與仿真所需加速度指令變化趨勢基本一致,當n=0時,加速度指令單調遞減;當0 表2 理想情況仿真結果 圖5 仿真曲線 考慮控制系統滯后,令控制系統響應時間Tm=0.3 s進行仿真,其結果見表3,其加速度指令與實際值見圖7。從表2與表3對比可以看出,控制系統滯后對飛行時間、末速、脫靶量、落角影響不大,但對終端過載影響嚴重,違背攻角收斂要求;結合圖7知,其原因是在滯后影響下在接近目標時加速度指令存在半震蕩甚至發散現象。因此實際工程應用時必須對終端加速度指令采取必要措施,如終端加速度指令歸零等。 表3 滯后情況仿真結果 主要解析結論如下: 1)該制導律簇可以克服初始位置誤差、初始瞄準方向角誤差以及常值目標機動干擾和實現終端落角約束;當0 圖6 解析解和仿真結果 圖7 帶滯后動力學時加速度變化 2)導引系數n決定著各項因素引起的無量綱化過載在時間軸上分配規律,其影響無量綱化過載曲線單調性、極點以及過零點,當n=0時,各無量綱化過載線性變化,而當0 3)制導時間tf決定著各項因素過載幅值規律,其中初始位置誤差引起的過載幅值與制導時間平方成反比,瞄準方向角誤差及終端落角約束引起的過載幅值與制導時間成反比,常值目標機動引起的過載幅值與制導時間無關。 4)從無量綱化視線角變化角度,4個因素極性不同將直接影響視線角變化趨勢。若瞄準角誤差與終端期望落角極性相反,有利于彈道成型。若常值目標機動與終端期望落角極性相同,有利于彈道成型。 基于上述結論,提出了工程應用設計準則。通過實例仿真,驗證了該制導律相關解析結論的有效性;指出了由于實際控制系統存在滯后影響,制導加速度指令終端變化劇烈現象不利于終端攻角收斂,需要采取終端攻角歸零措施。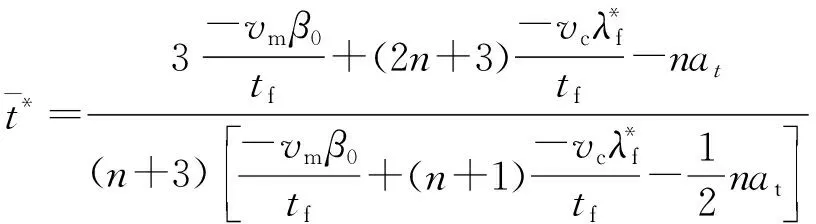

4 數學仿真
5 結論