具有連續纖維目標的圖像拼接研究
韓子葉,王榮武
(東華大學紡織學院,上海 201620)
0 引言
隨著信息的發展與科技的進步,數字化圖像處理技術在紡織領域的應用愈來愈廣泛,較傳統的紡織檢測技術更加客觀、高效。在進行數字化檢測的過程中,通常使用光學顯微鏡對原始圖像進行采集。由于光學顯微鏡的成像原理等原因,得到的圖像會存在清晰度與視野不可兼得的矛盾[1]。如果選擇較高的放大倍數,得到的圖像更清晰、細節更明顯,但是視野較小,無法對材料進行全面的分析;相反,如果選擇的放大倍數較低,會得到視野較大的圖像,但是清晰度低,不能進行細節觀察,得到的分析結果精確度不足。因此,采用圖像拼接技術,將多個具有較高放大倍數的小視野圖像拼接成為一幅大視野圖像,使獲得的圖像包含清晰細節的同時視野更廣。
1 基于SIFT算法的圖像拼接
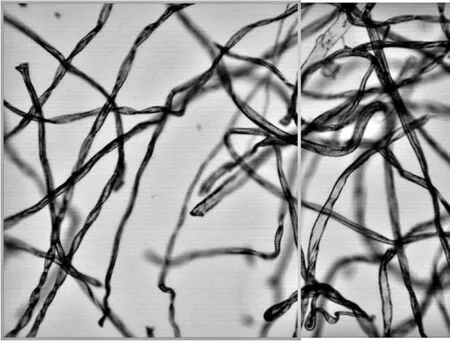
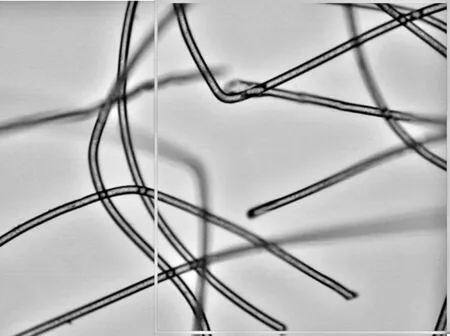
本實驗采用2#國際標準羊毛纖維作為實驗數據,在BEION M318全自動光學顯微鏡下,使用4X平場無限遠物鏡組對圖像進行采集,采集到的圖像大小均為800×600(x方向為800,y方向為600)。為了將兩幅相鄰的纖維圖像進行拼接,要求兩幅圖像具有一定的重疊區域。對于M318顯微鏡的4X物鏡組,可設定顯微鏡載物平臺在X軸正方向移動步長為300,采集到的圖像如下圖1所示。
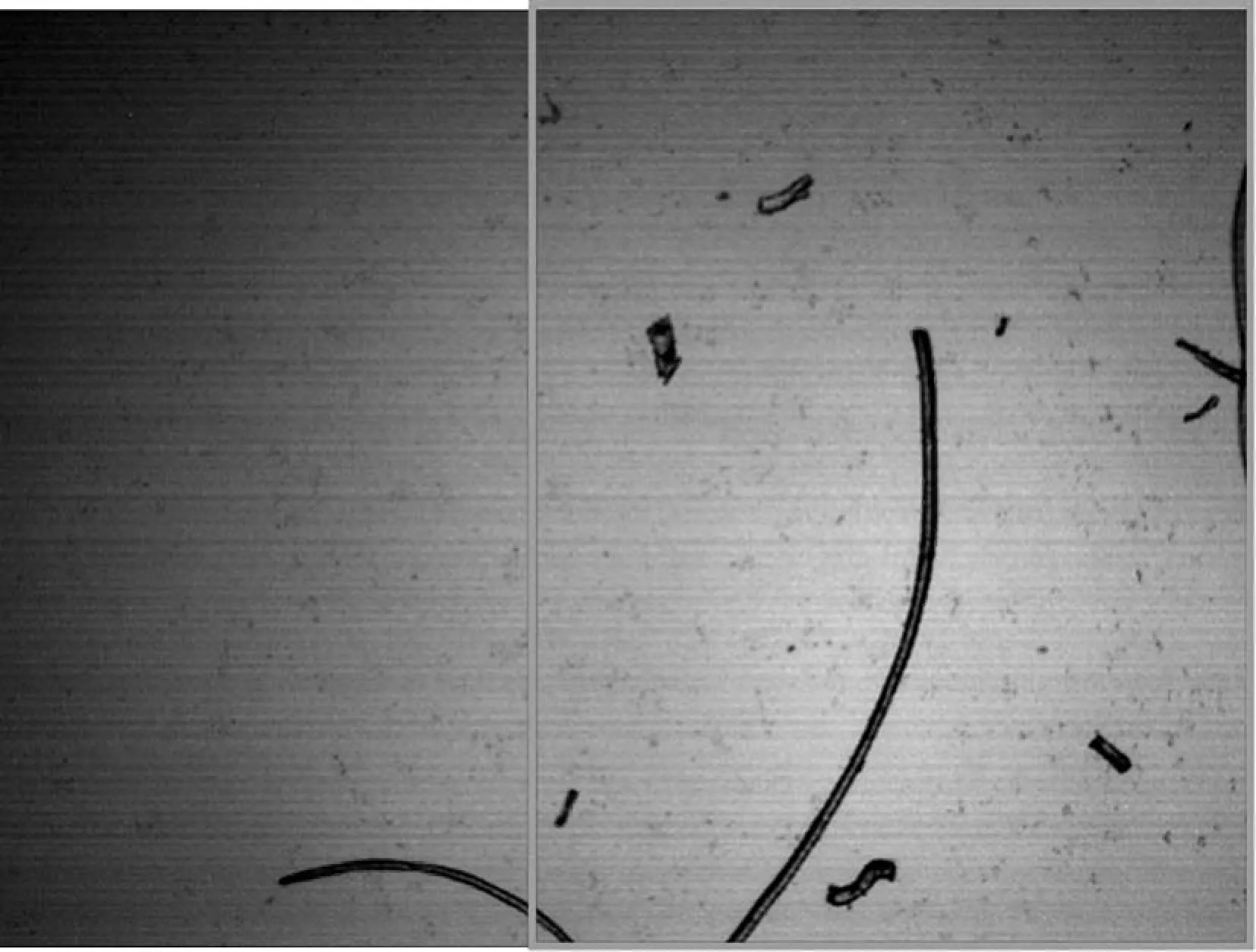
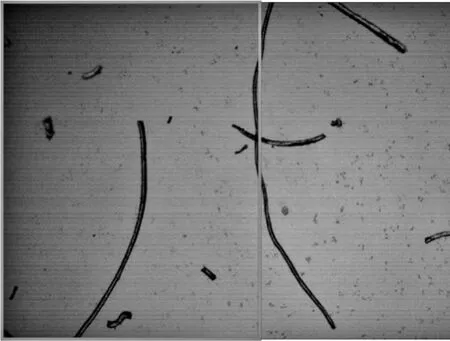
圖1 采集到的連續羊毛纖維圖像
圖像中紅色線框所標注的部分即是兩幅圖像間的重疊區域。如上圖1所示,重疊率大致達到了60%。
由圖1可以觀察到,當圖像中纖維分布較為分散時,纖維根數少,包括大片的空白區域,含有的可用信息少。基于上述的圖像特點,所采用的圖像拼接算法需要具有“多量性”特征,即含有少量的物體也可以檢測出大量的特征點用來進行匹配。在眾多具有此性質的圖像拼接算法中,SIFT算法是典型代表。SIFT算法于1999年由Lowe等人提出后于2004年總結完善[2],其原理是首先構建圖像高斯差分金字塔,在相鄰尺度上通過選取指定區域中的極值點來提取候選特征點,再通過三維二次函數擬合精確關鍵點的尺度和位置,同時消除邊緣響應點和低對比度的點。同時為了滿足特征點的旋轉不變性,為每一個特征點分配一個主方向并且對坐標軸進行變換。將特征點的鄰域進行劃分,為特征點生成128維的特征向量對其進行描述。之后采用歐式距離作為指標以衡量兩個向量間的相似性,在此基礎上對圖1中的兩幅圖像進行圖像拼接,得到的結果如下圖所示。
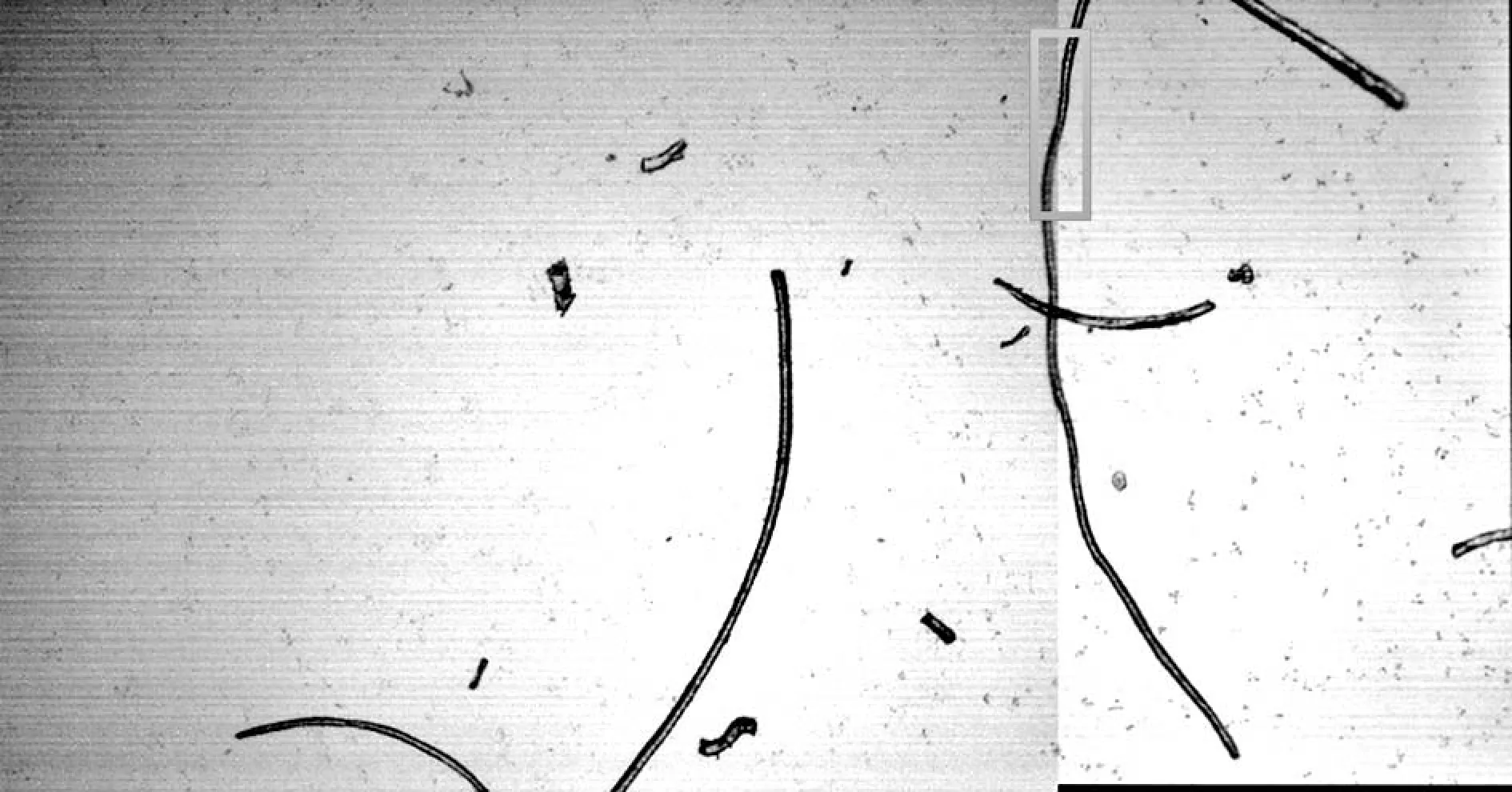

圖2 拼接圖像
圖2中上方圖像為圖1中兩幅圖像拼接后原圖,圖2下方圖像為拼接處的局部放大圖。可以看出對于毛纖維,當纖維分布稀疏時,SIFT算法的拼接效果良好,但是由于圖像采集時點光源影響,兩幅相鄰圖像有光照差異,造成拼接后的圖像具有拼接線,因此需要通過圖像融合技術消除此線。
2 圖像融合
圖像融合一方面是要利用待拼接的兩幅圖像中重疊區域外的不同信息進行互補,使得有用信息在最大程度上保留在配準融合后的圖像中,二是消除拼接縫隙,使得兩幅圖像之間的過渡更加自然、平滑,具有一個良好的視覺效果[3-4]。
本文采用漸入漸出法進行融合。其原理是對位于重疊區域的像素進行加權。權重的選擇取決于重疊區域中的像素位置距離其邊界的遠近,距離越遠,權重越小。f1和f2表示待拼接的兩幅圖像,f表示融合后圖像,(x,y)表示像素點的具體坐標,則有:
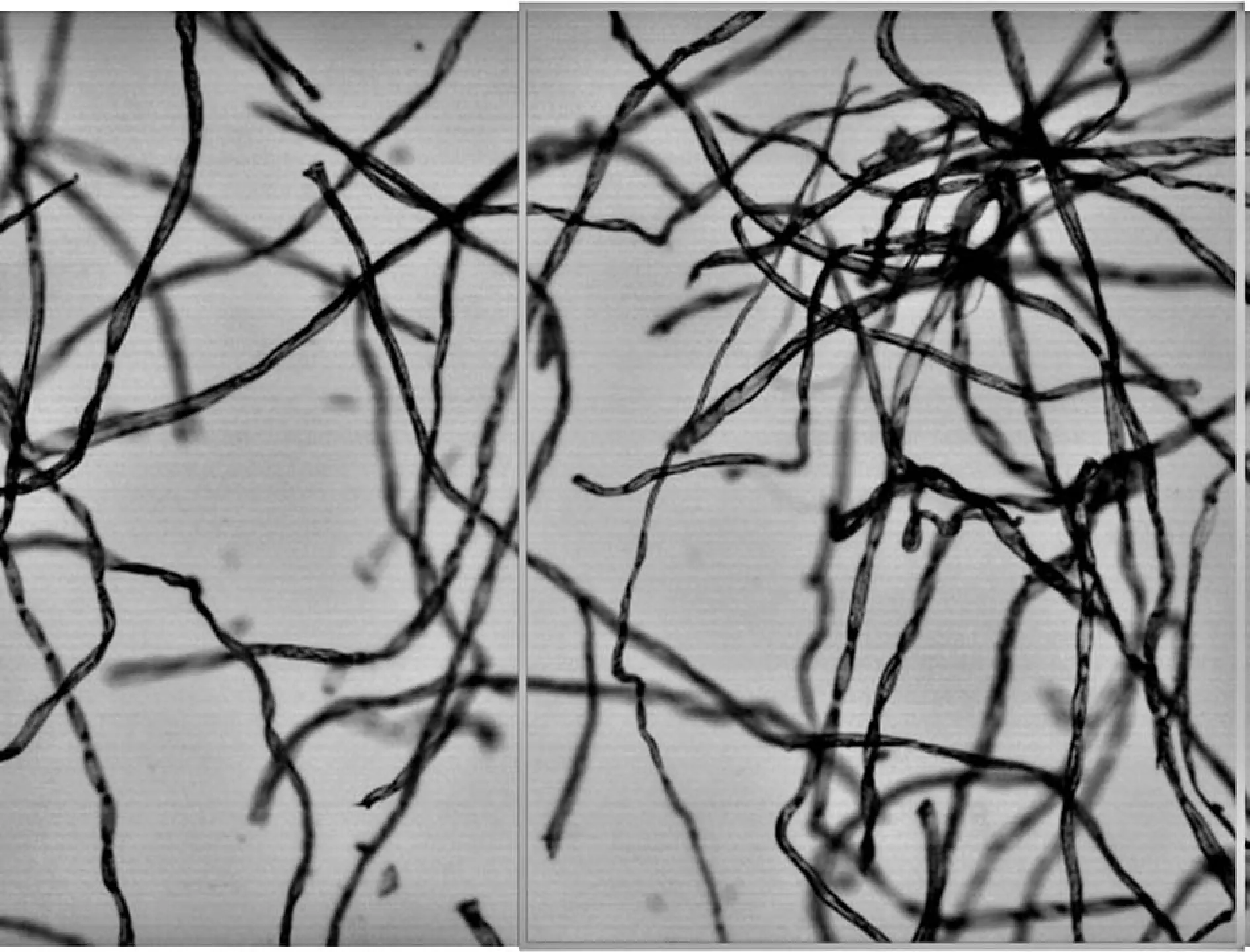
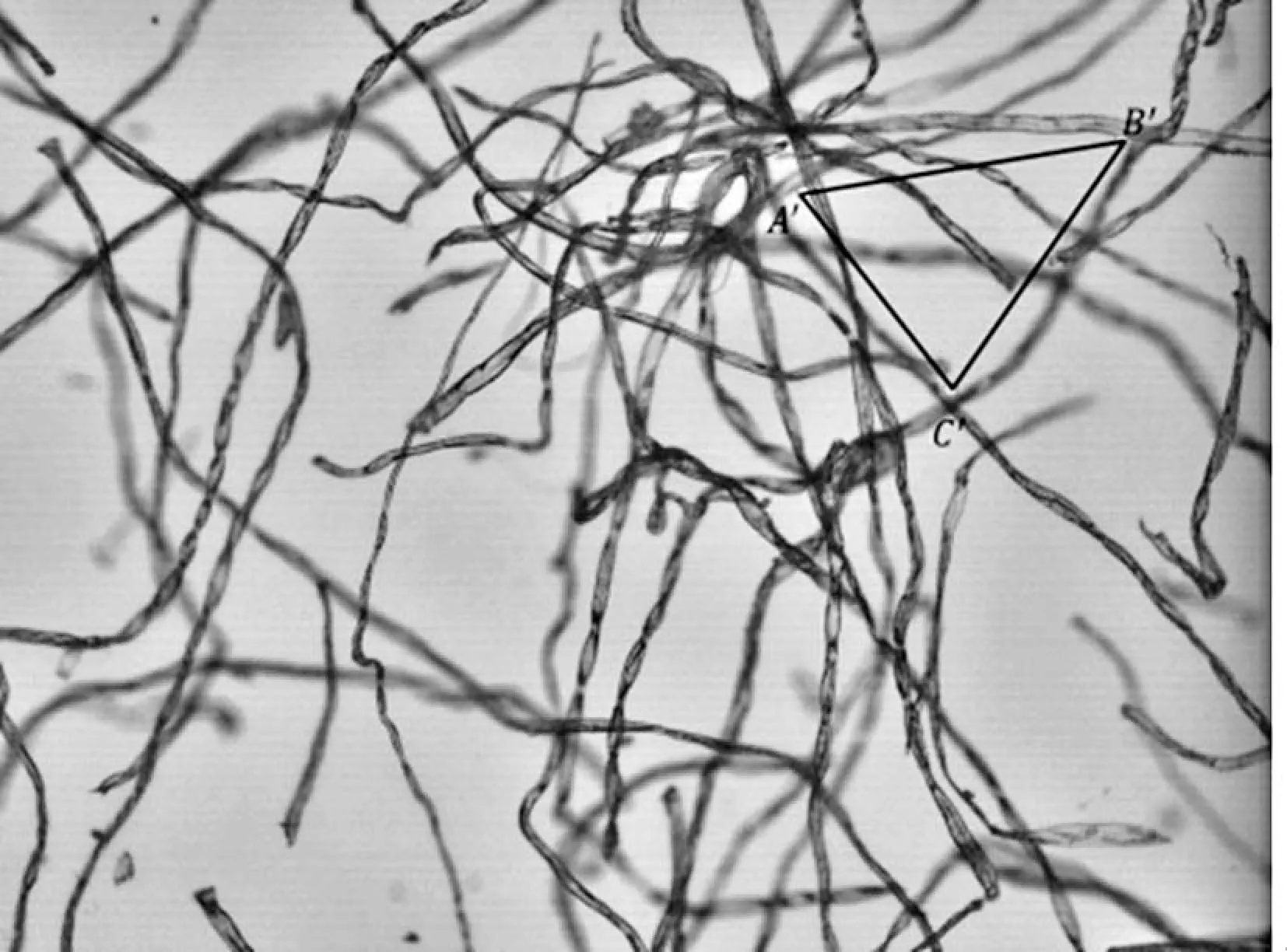
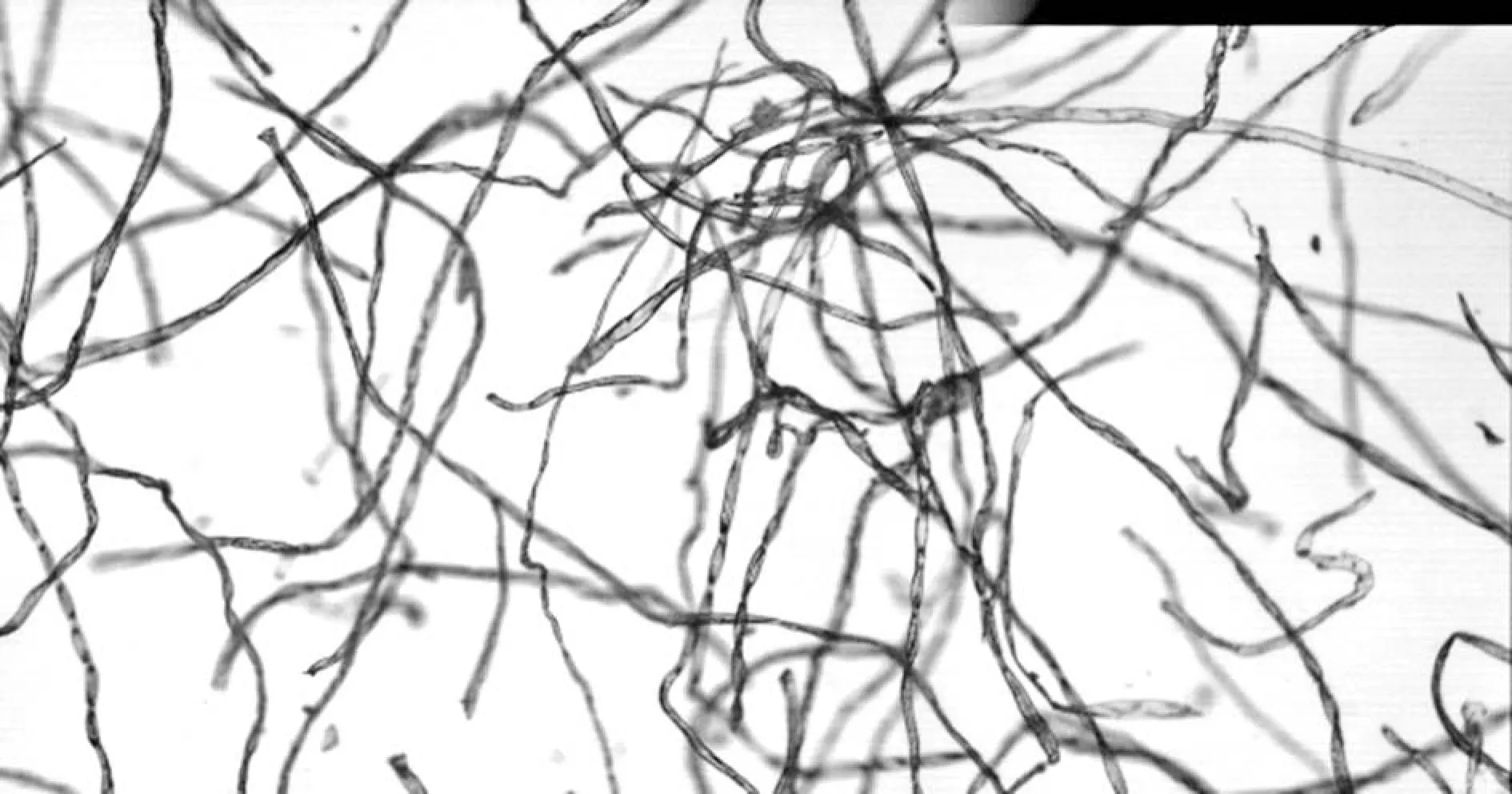
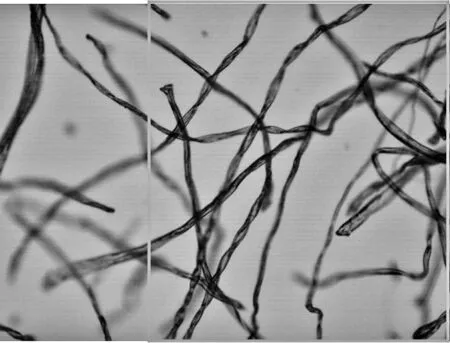
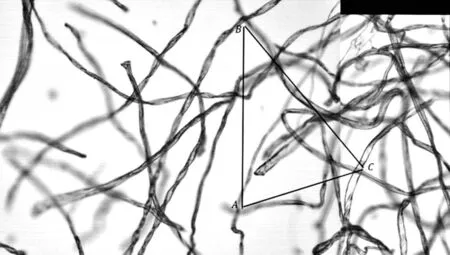
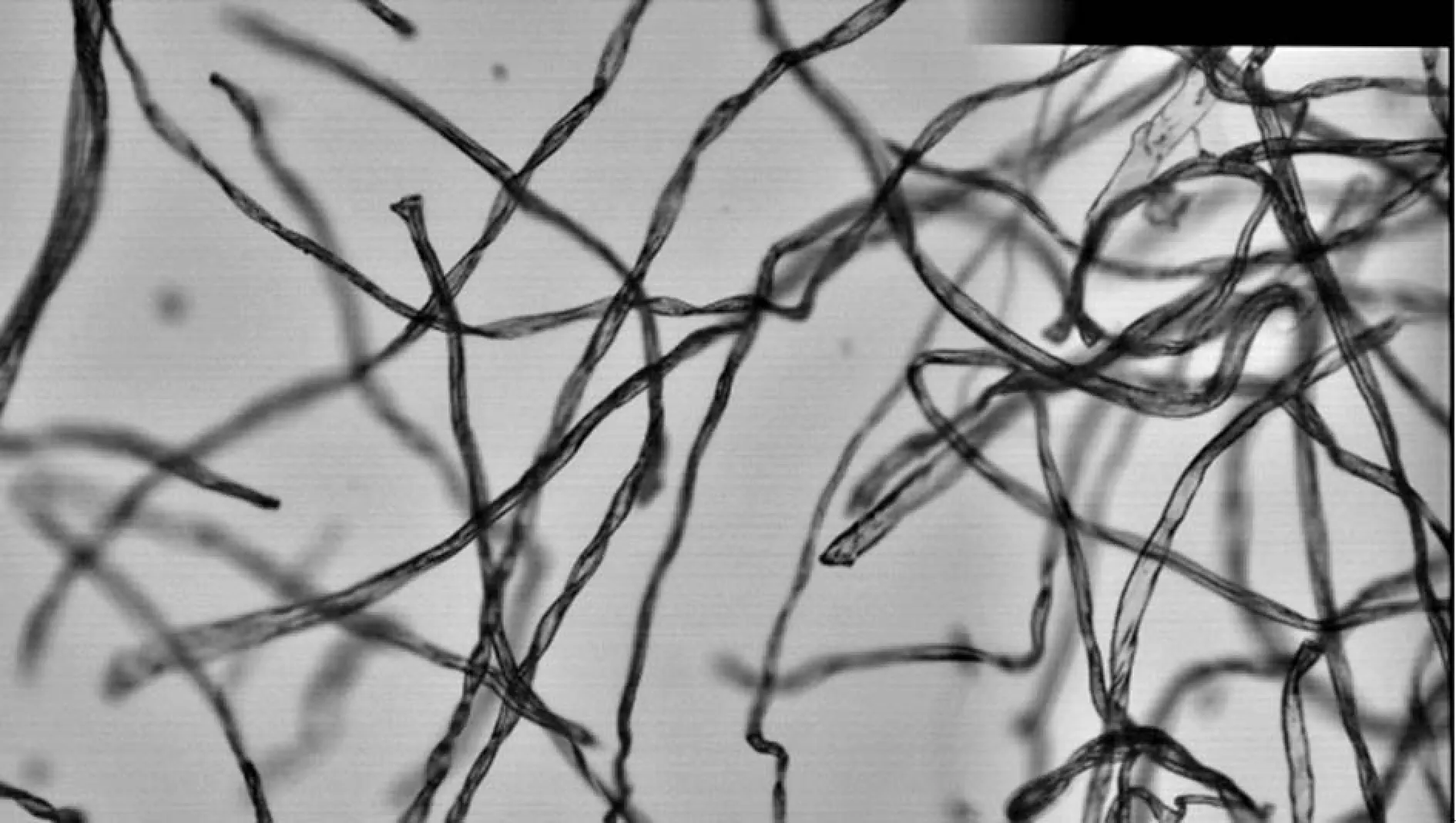
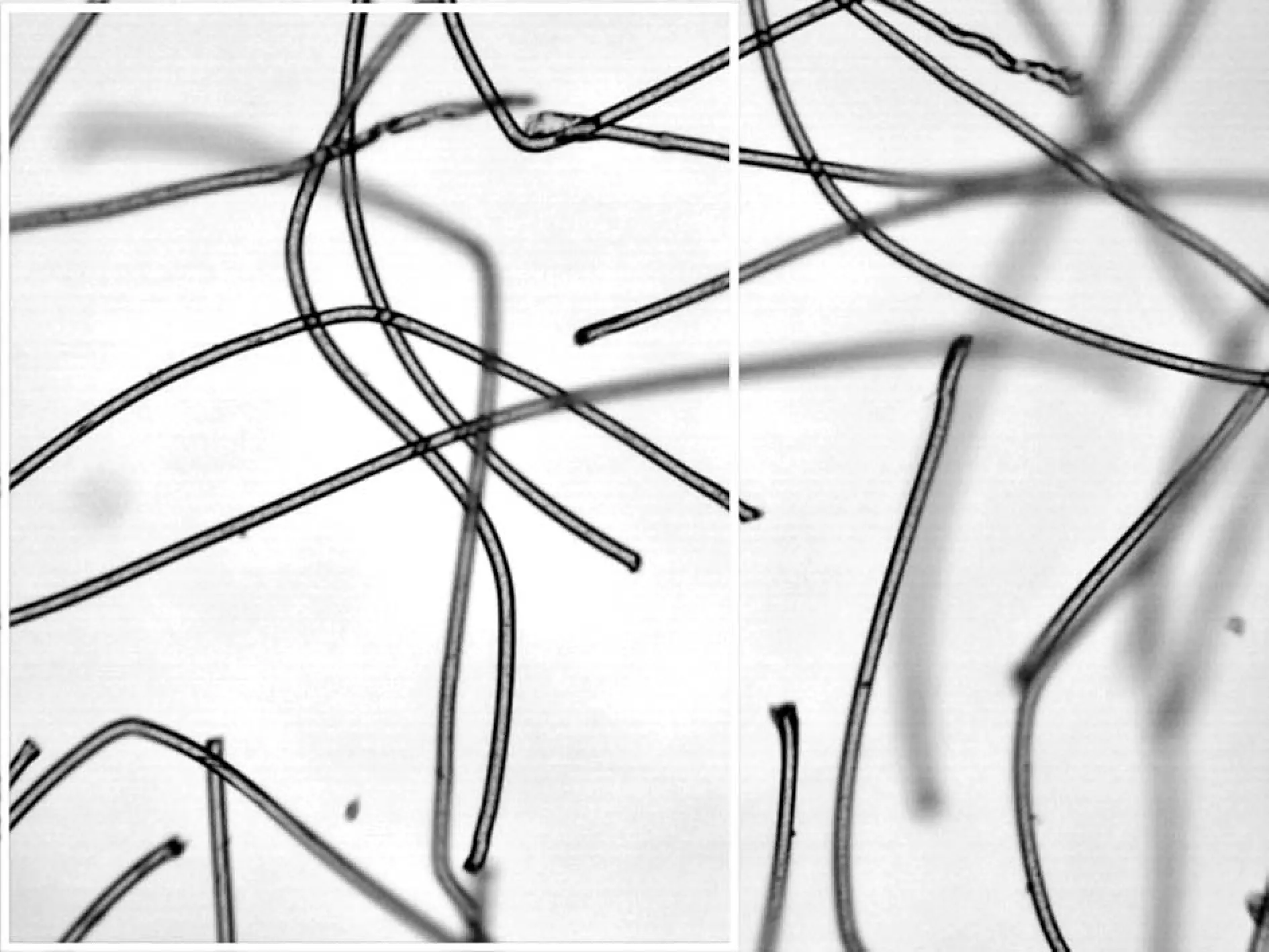
式中,d1和d2表示權重,并且d1+d2=1,0 圖3 漸入漸出法原理圖 對圖2中上方圖像進行漸入漸出法融合的結果如下圖4所示。 圖4 融合效果圖 可以看出,經過漸入漸出法融合之后,在拼接處存在著的拼接線已經消失,并且信息沒有明顯損失,得到了視覺效果良好的拼接圖像。 上述實驗所采用的圖像為羊毛纖維的圖像,并且纖維分布稀疏,得到的拼接效果良好,但是由于紡織材料的廣泛性,其纖維原料多樣、纖維分布的形式多樣以及顯微鏡的倍數多樣。因此,需要在不同的情況下對此算法進行驗證實驗。本實驗采用天然纖維中的棉纖維、化學纖維中的滌綸纖維以及非織造材料等圖像進行驗證。 棉纖維具有良好的吸濕和透氣性能,并且手感柔軟,透氣性好,被廣泛地應用于紡織領域中。在上文采用羊毛纖維進行實驗時,圖像中纖維分布稀疏。因此,為了驗證算法在纖維分布密集時的拼接以及融合效果,在使用棉纖維圖像進行驗證時,使纖維分布密集,并在4X物鏡組與10X物鏡組下分別獲取圖像。 圖5 4X物鏡組下采集的連續兩幅密集棉纖維圖像 在4X物鏡組下對分布密集的棉纖維進行圖像采集,得到連續的兩幅圖像,其中纖維含量多,包含的信息更為復雜,如圖5所示。拼接結果以及拼接結果的驗證如下圖6所示。 (a) (b) 圖6(a)為圖5中兩幅圖像進行拼接的結果,圖6(b)中則包含了拼接圖像中拼接線周圍完整的圖像信息,在(a)、(b)兩幅圖像中于拼接線周圍選擇三個同樣的特征點進行連接,得到了兩個全等三角形,表明SIFT算法適用于低倍數下密集纖維圖像的拼接,會得到良好的拼接效果。對6(a)采用漸入漸出法進行圖像融合的結果如下圖7所示。 圖7 圖6(a)中圖像融合后結果 由融合后圖像與融合前圖像進行對比可以看出融合效果良好,既保留了非重疊區域的圖像信息,使其完整,又消除了拼接縫隙,使整個圖像過渡自然。 圖8 10X物鏡組下采集的連續兩幅密集棉纖維圖像 由圖8可以看出,與低倍物鏡組下采集到的纖維分布密集時的圖像相比,高倍鏡下多焦面現象更為明顯,當纖維數量較多時,在空間中產生“堆疊”,即同一幅圖像中纖維存在不同焦面上,無法同時表現出清晰的狀態,對圖像進行連續采集時,位于兩幅圖像中的同一點并不能保證會是同一個清晰狀態,因此增加了拼接難度。對圖8中兩幅連續圖像進行拼接,結果與拼接效果驗證如下圖9。 (a) (b) 圖9(a)為采集到的10X物鏡下連續兩張密集棉纖維圖像進行拼接的結果,圖9(b)則為4X物鏡下采集到的同位置圖像,包含了完整的圖像信息,在(a)(b)兩幅圖像中于拼接線周圍選擇三個同樣的特征點進行連接,得到了兩個相似三角形,表明SIFT算法對于尺度具有良好的魯棒性,適用于高倍數下密集纖維圖像的拼接。對圖9(a)使用漸入漸出法進行圖像融合的結果如下圖10所示。 圖10 圖9(a)中圖像融合后結果 由融合結果可以看出,該融合算法同樣適用于具有多焦面現象的纖維密集分布圖像。 滌綸纖維是一種常見的化學纖維,具有耐沖擊性、彈性好等特點,被廣泛地應用于紡織領域。本文分別使用4X物鏡組和10X物鏡組對滌綸纖維圖像進行采集,對本文中的算法進行驗證。 圖11 4X物鏡組下采集的連續兩幅滌綸纖維圖像 拼接結果以及拼接結果的驗證如下圖12所示。 (a) (b) 圖12(a)為圖11中兩幅圖像進行拼接的結果,圖12(b)中則包含了拼接圖像中縫隙周圍完整的圖像信息,同樣在4X物鏡組下拍攝,在(a)、(b)兩幅圖像中于拼接縫隙周圍選擇三個同樣的特征點進行連接,得到了兩個相等三角形,表明SIFT算法適用于低倍物鏡組下滌綸纖維圖像的拼接。 在10X物鏡組下對滌綸纖維進行采集的圖像如下圖13。 圖13 10X物鏡組下采集的連續兩幅滌綸纖維圖像 拼接結果以及拼接結果的驗證如下圖14所示。 (a) (b) 圖14(a)為采集到的10X物鏡下連續兩張滌綸纖維圖像進行拼接的結果,圖14(b)中則包含了拼接圖像中縫隙周圍完整的圖像信息,在4X物鏡組下拍攝,在(a)、(b)兩幅圖像中于拼接縫隙周圍選擇三個同樣的特征點進行連接,得到了兩個相似三角形,表明SIFT算法適用于高倍物鏡組下滌綸纖維圖像的拼接。 非織造材料是由纖維直接構建而成,因此非織造材料圖像亦是纖維目標圖像。因為本實驗圖像由光學顯微鏡獲取得到,由于透光的問題,要求非織造材料的厚度在一定范圍內,便于光透射進行圖像采集。因此,本實驗采用紡粘非織造材料進行拼接,并對拼接效果進行驗證。 本實驗對紡粘非織造材料在20X物鏡組下的圖像進行采集拼接,在20X物鏡組下對紡粘非織造材料進行采集的圖像如下圖15。 圖15 20X物鏡組下采集的連續兩幅紡粘材料圖像 拼接結果以及拼接結果的驗證如下圖16所示。 (a) (b) >圖16(a)為采集到的20X物鏡組下兩張連續的紡粘非織造材料圖像進行拼接的結果,圖16(b)中則包含了拼接圖像中拼接線周圍完整的圖像信息,在10X物鏡組下采集得到,在(a)、(b)兩幅圖像中于拼接線周圍選擇三個同樣的特征點進行連接,得到了兩個相等三角形,表明SIFT算法適用于高倍物鏡組下纖維信息復雜的紡粘非織造材料圖像的拼接。 使用漸入漸出法對SIFT算法拼接后的圖像進行融合,可以消除因光照差異等原因產生的拼接線。通過使用棉纖維圖像、滌綸纖維圖像以及紡粘材料的圖像對上述算法進行驗證,該算法可以廣泛地應用于紡織領域。通過對纖維圖像進行拼接,使纖維目標更加完整化,獲得更加精確全面的纖維信息,在數字化檢測的過程中得到應用,如增加纖維直徑的測量精度;擴展了圖像視野,可以得到材料本身更加完整的信息,如材料的孔隙率、取向度、混紡比等性能。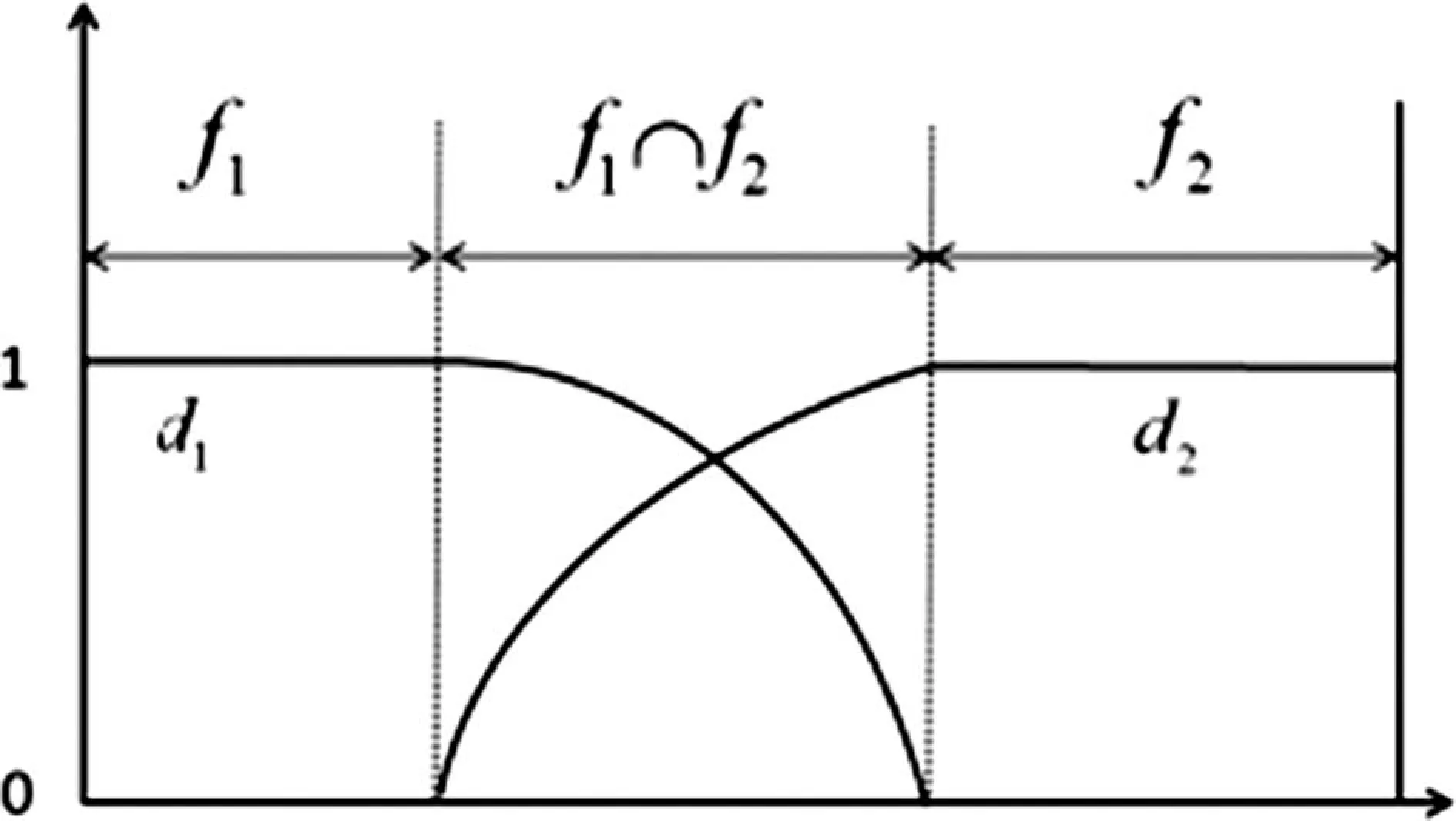

3 廣泛性驗證
3.1 使用棉纖維圖像進行驗證



3.2 使用滌綸圖像進行驗證






3.3 非織造材料圖像




4 結論

