約束無跡粒子濾波及其在汽車導航中的應用

洪晉夫，劉錦昌

（1.山西省交通科學研究院，太原 030006；2.空軍工程大學防空反導學院，西安 710051）

0 引言

全球定位系統［1］具有全天候導航、實時性強、定位精度高的優點，但是也具有數據頻率較低，受衛星信號強度影響大以及數據可靠性低的缺點。導航推算系統［2］是一種利用方位和速度信息計算汽車位置信息的自主導航系統，在較短時間里具有高精度、高頻率、高可靠性的特點，但是隨著時間的增長，導航提算系統會隨著自身誤差的積累而出現發散現象，需要外部導航定位信息提供信息校準，全球定位系統恰恰滿足導航推算的長時間導航信息校準要求。兩種系統的深度融合可以取長補短，發揮自身優勢，為汽車提供長時間可靠精確導航定位信息。近年來這種組合導航定位系統［3-5］已經逐漸成為理論研究的熱點問題。

組合導航定位系統是一種高維非線性系統，對于組合導航定位系統的濾波算法的研究近年來也取得了很多成果。擴展卡爾曼濾波［6-7］通過對非線性系統進行一階泰勒展開進行局部線性化來進行濾波，具有計算量適中，迭代估計方便的優點，但是當系統的非線性較高時會出現估計的誤差較大甚至發散的缺點，并且當系統的維數較高并且較復雜時，計算雅克比矩陣的難度加大甚至無法求取，計算效率降低，無法滿足組合導航系統的要求。粒子濾波［8-13］具有對非線性高維系統適應性強的特點，文獻［11］提出利用擴展卡爾曼濾波和粒子濾波結合的擴展卡爾曼粒子濾波算法，改善了擴展卡爾曼濾波的性能，但是由于依然采用了線性化處理，濾波精度有待提高。無跡卡爾曼濾波［14-15］采用無跡變換預測下一時刻的值，避免了線性化的過程，提高了運算精度。文獻［16］將無跡卡爾曼濾波與粒子濾波結合，用無跡卡爾曼濾波生成粒子濾波的采樣點，提出了無跡粒子濾波算法，提高了算法的精度。但是無跡粒子濾波同樣存在隨著系統維數提高，計算量上升很快，對于組合導航這種對實時性要求很高的系統，計算效率遠遠滿足不了要求。本文將約束方程引入無跡粒子濾波算法中，提出一種改進的約束粒子濾波算法，約束方程的引入可以降低系統的維數，使算法的計算量大大降低，實時性提高，并且保證了運算的精度，通過汽車導航定位系統的仿真，驗證了算法的優越性。

1 約束無跡粒子濾波算法

1.1 CUPF算法設計

非線性系統可以用下式表述：

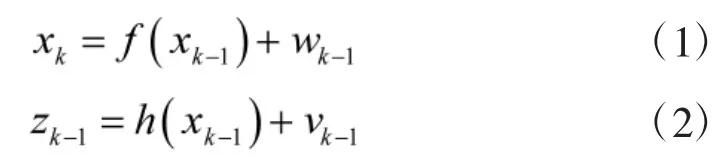
式中，xk是k時刻狀態變量，zk是測量值，f（·）和h（·）為非線性函數，wk是過程噪聲，vk是量測噪聲。

構造狀態量xk的約束方程為

其中，D與d分別是狀態變量的約束矩陣與約束向量。約束無跡粒子濾波算法過程如下：

1）初始值，令k=0，從先驗概率函數p（x0i）中取一個樣本 x0i，i=0，1，2，…，2n。

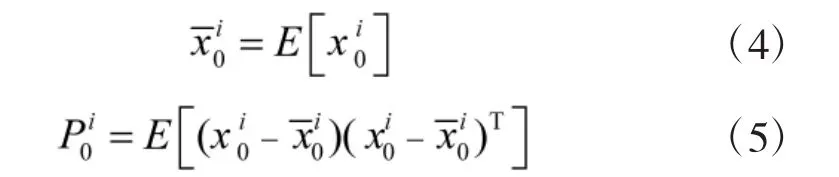
2）狀態擴維

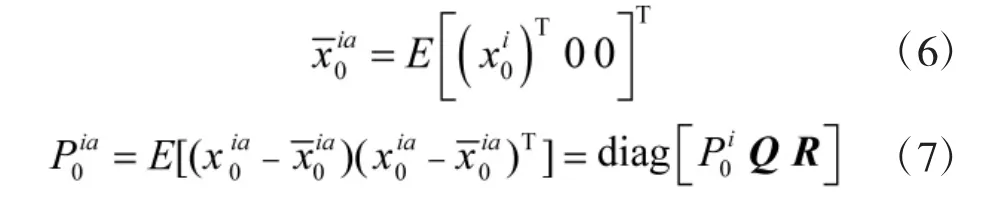
其中，Q與R分別wk與vk的協方差矩陣。

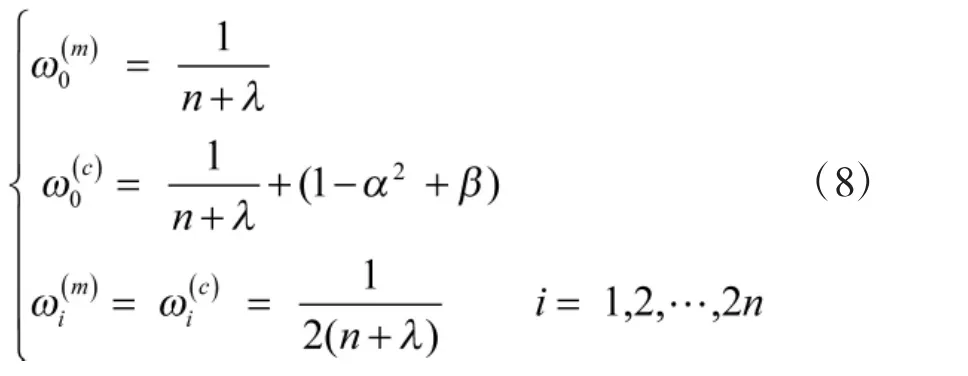
3）令 k=1，2，…

（1）重要采樣

i=0，1，2，…，2n 時，采用無跡卡爾曼濾波更新粒子。

①粒子值

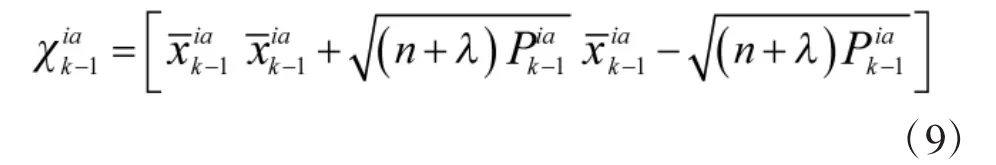
②一步預測

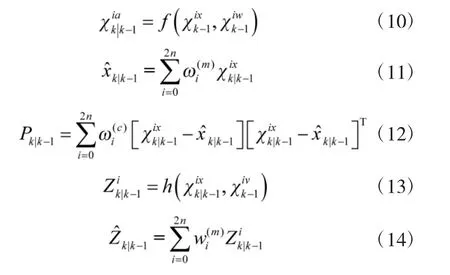
③更新值

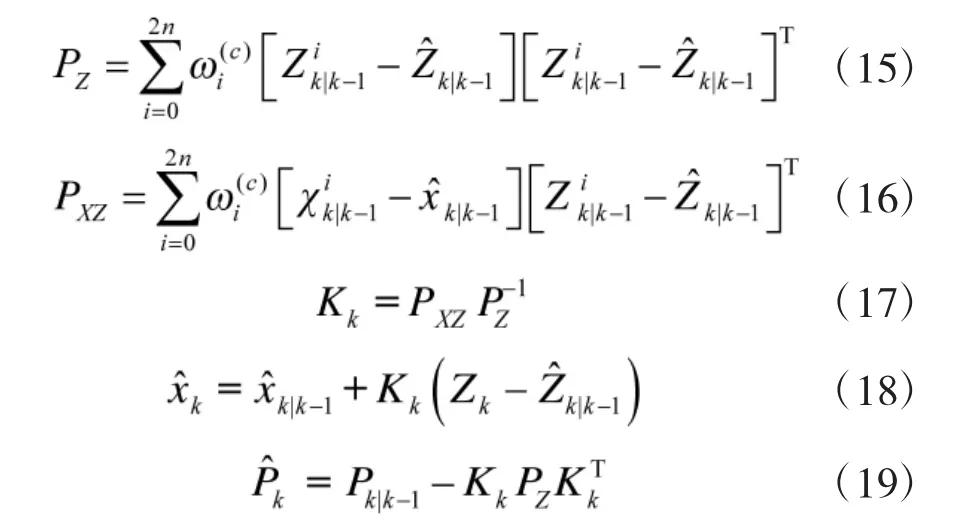
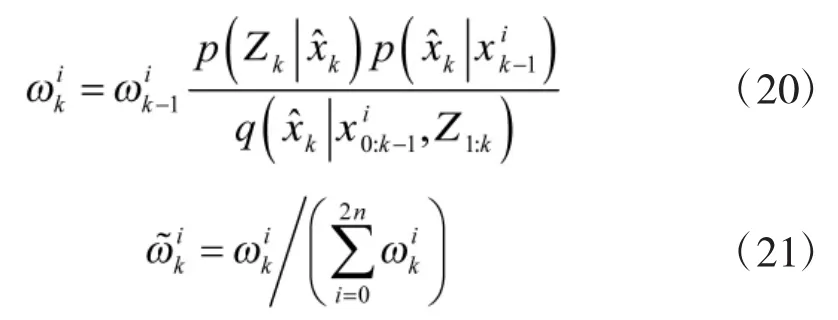
（2）重采樣

Neff為有效粒子數，NT為有效粒子數閾值，如果Neff＜ NT，則進行重采樣，重采樣之后新的粒子為，歸一化權值為。

（3）結果

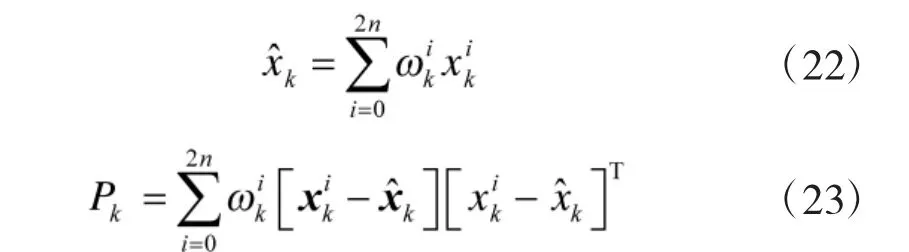
4）約束值計算

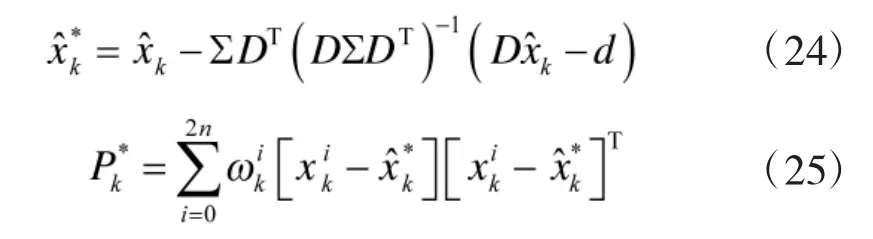
可得CUPF濾波算法的狀態值。

2 CUPF在汽車導航中的應用

2.1 汽車導航系統

2.1.1 組合系統狀態方程

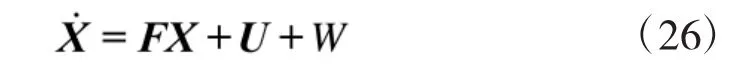
式中，F是狀態轉移陣，U是控制陣，W是噪聲。

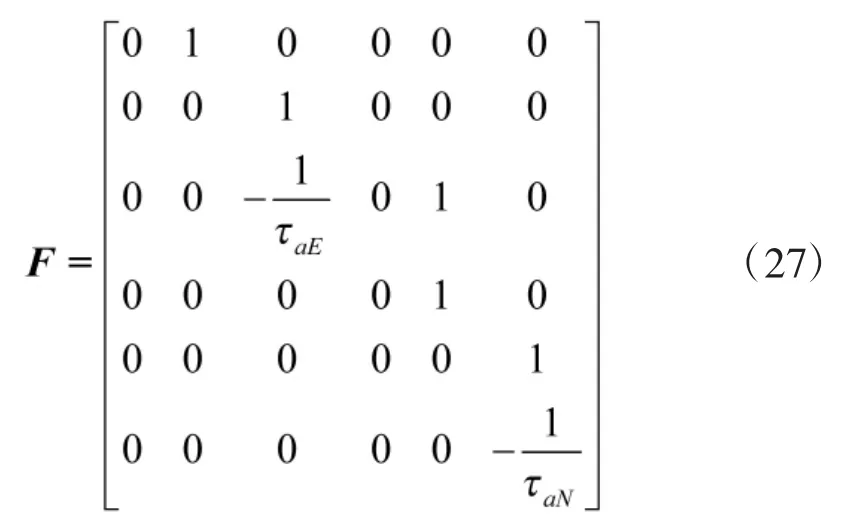
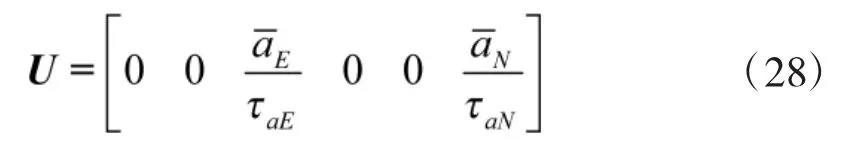
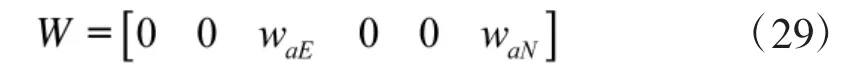
2.1.2 量測方程

汽車導航系統的量測值為

式中，xe和xn分別為全球定位系統顯示的東向和北向的位置，ω為電子羅盤顯示角速率，s為里程表顯示數。量測方程如式（31）

式中

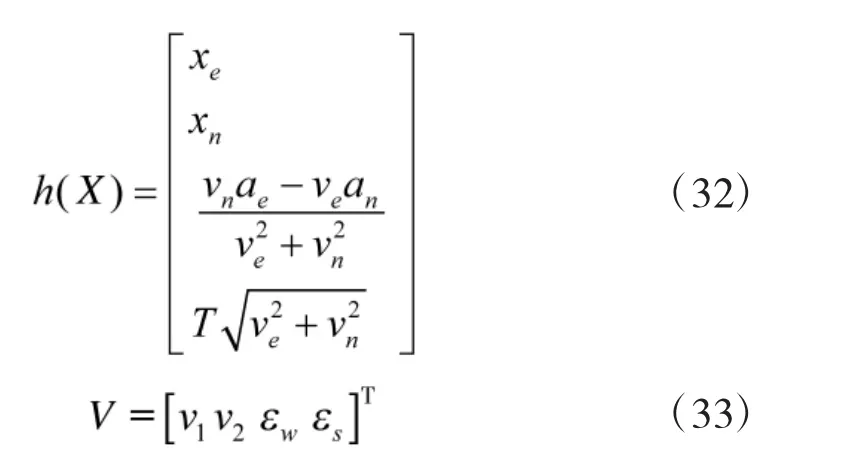
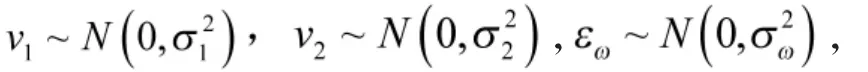
2.2 約束方程

2.2.1 運動約束方程

根據運動學定理中位移、速度和加速度之間的關系可得汽車運動滿足下式

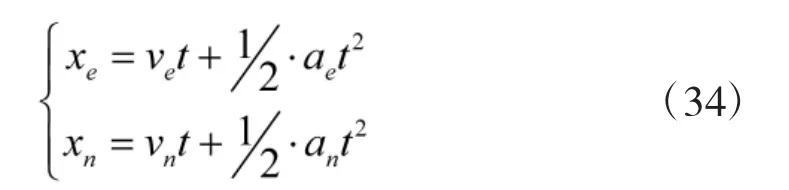
因此，運動約束為

式中，矩陣D1與向量d1分別是：

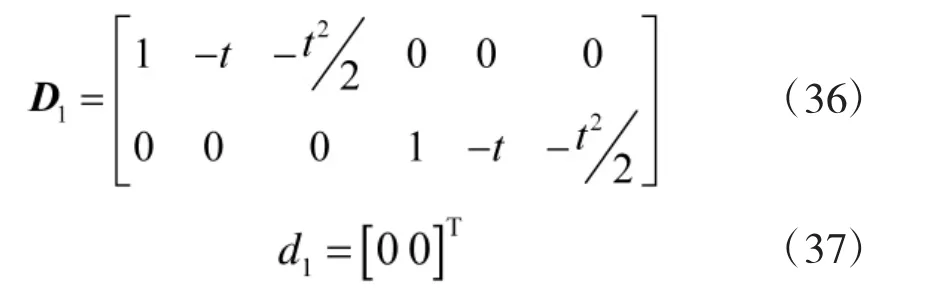
2.2.2 道路約束方程

汽車行駛過程中，必須在道路范圍內運動，如果超出道路的范圍，必須對汽車的運動進行約束才能使其在正確的范圍內行駛，行駛范圍如下頁圖1所示。

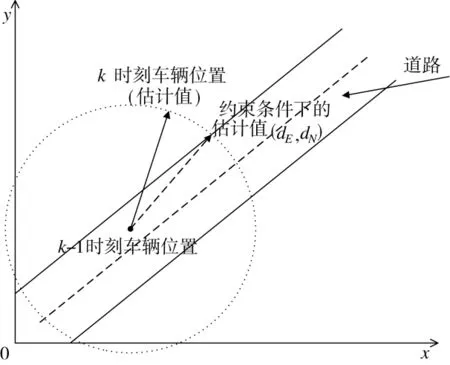
圖1 汽車的行駛范圍

式中，de和 dn是已知道路的位置。（de，dn）是以 k-1時刻汽車的位置為圓心、以k-1至k時段內汽車的位移為半徑的圓與道路邊線相交的位置，此位置最接近估值。由式（13）可得：

其中，矩陣D2和向量d2分別為

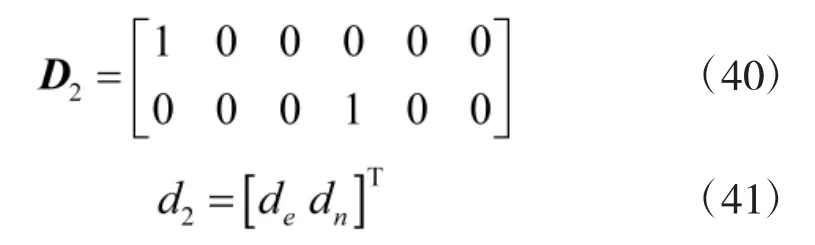
2.2.3 導航系統總約束方程

式（10）和式（14）構成了汽車導航系統總約束方程，聯立式（10）和式（14）可得：

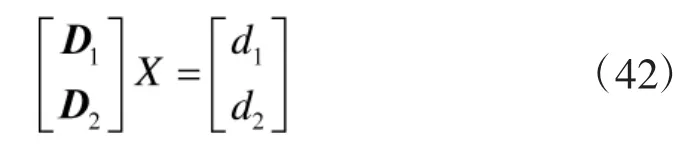
3 仿真與分析

汽車導航系統的仿真參數如表1所示。

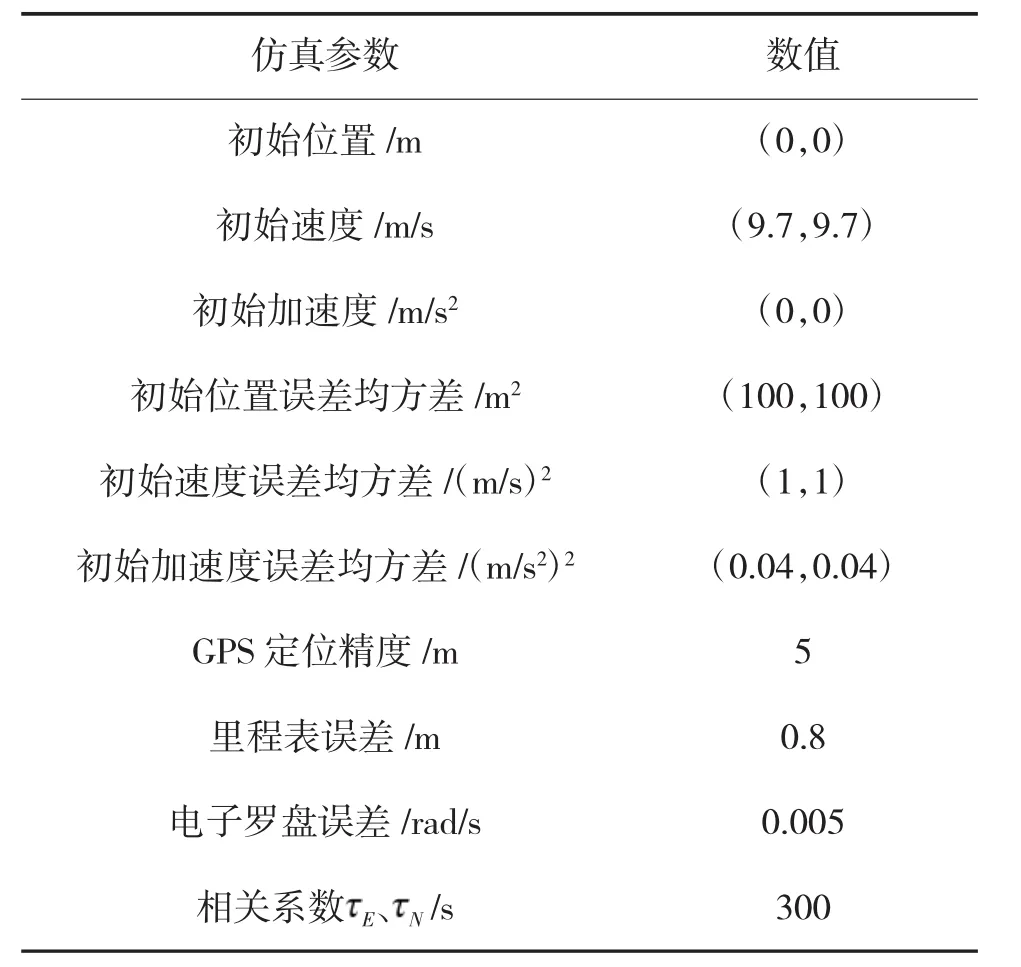
表1 仿真參數設置

設道路中線過原點，沿正東北方向，路寬10 m。仿真總的時長設為600 s。分別采用擴展粒子濾波算法（EPF）和無跡粒子濾算法（UPF）算法及本文算法進行仿真，粒子數選為50，仿真結果如圖2和圖3所示。

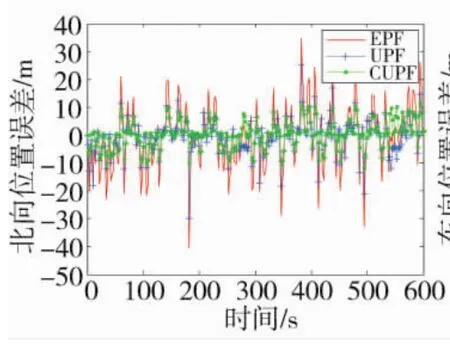
圖2 北向位置誤差

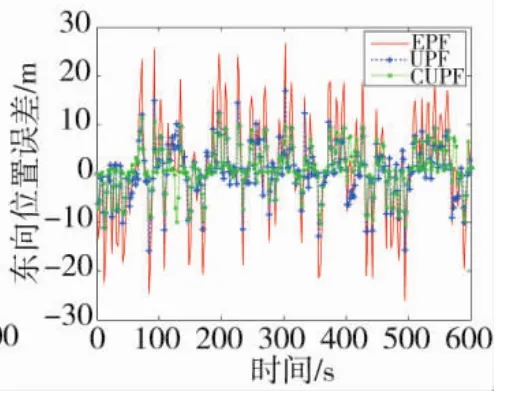
圖3 東向位置誤差

為了進一步分析算法的性能，計算各種算法的均方根誤差RMSE大小，公式如下：

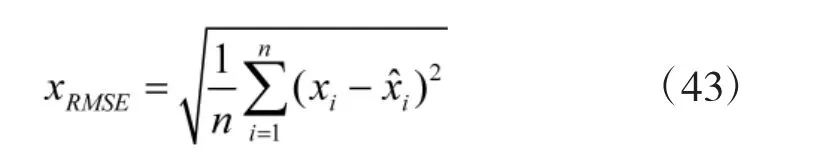
xRMSE表示算法估計的精度大小，均方根誤差越小表明算法的精度越高。3種算法分別進行50次，將每次運算的xRMSE取平均值得到算法的平均均方根誤差，將每次運算的時間取平均值得到算法的平均運行時間，表2列出了3種算法的平均均方根誤差和平均運行時間。

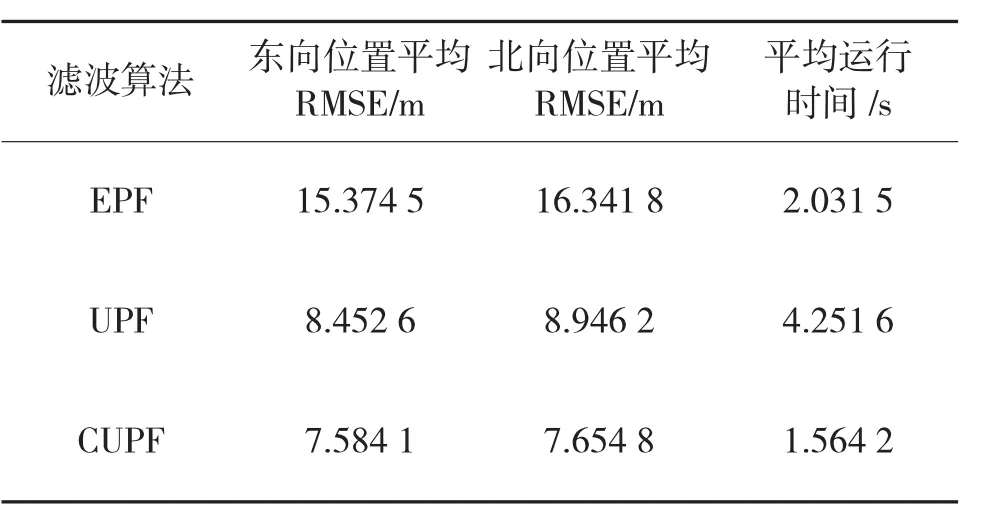
表2 3種算法的性能分析

從圖2和圖3以及表1可看出，EPF濾波算法的穩定性比較差，有很多跳變的點，算法的誤差較小，位置平均RMSE在3種算法中最大，在汽車導航系統中，對算法的穩定性和誤差要求很高，EPF算法無法滿足汽車導航系統的要求。UPF濾波算法的精度較高，沒有跳變的點，穩定性較高，但是算法的平均運行時間在3種算法中最高，說明算法的實時性較差，在汽車導航系統中，算法的實時性將關系到汽車導航系統的操控性，UPF算法無法滿足汽車導航系統的實時性要求。本文提出的CUPF算法的誤差最小，導航的精度最高，穩定性也較好，算法的運行時間最小，實時性較好，能夠滿足汽車導航系統的要求。通過比較，可以看出本文提出的算法在3種算法中性能最好，體現了算法的優越性。

4 結論

針對現有各種濾波算法的不足，本文將約束方程引入無跡粒子濾波算法，提出一種約束無跡粒子濾波（Constraints Unscented Particle Filter，CUPF）算法，此算法既保持了無跡粒子濾波的高精度特點，又通過約束方程的引入降低了系統維度，提高了算法的實時性。分析了汽車導航系統中存在的約束方程，將此算法應用到汽車導航系統中，仿真結果表明，本文提出的算法估計精度較高，算法的穩定性較好，算法所用時間較短，運算性能明顯高于擴展粒子濾波和無跡粒子濾波算法，可以滿足汽車導航系統的要求。