基于翼型凹變的葉片結構動力學性能優化方法研究

馬劍龍，霍德豪，李學彬，段亞范，吳雨晴，汪建文

(1.內蒙古工業大學 能源與動力工程學院，呼和浩特 010051；2.風能太陽能利用技術教育部重點實驗室，呼和浩特 010051)

隨著風能多元化應用推廣的深入，風力機翼型和葉片的成功開發是風力機設計中提升風能利用率、解決機組運行失穩和結構疲勞損傷的基礎性問題。然而，風力機產業快速發展的30年中，諸多氣動性能優異的分布式風電葉片在遠短于設計壽命期內頻發疲勞損傷事故而導致產品夭折的事件屢見不鮮。分析其原因：由于風力機葉片朝著大型化的方向發展并采用輕型材料，使得葉片柔性增大、結構剛度降低、固有頻率下降。此外，在實際運行中葉片在吸力面處的氣流交匯也會更加的復雜，使得葉片氣動性能及運行穩定性上有大幅度的下降。進而導致葉片振動響應增強，疲勞損傷加劇。介于此，在分布式風力機現有翼型成果基礎上提出一種即可保持葉片氣動性能，亦可有效改進其結構動力學性能的結構改進方案不失為一種技術捷徑。之前的研究中，研究人員對葉片的結構改形多著眼于翼型前、后緣點處結構形式的改進，本文擬另辟蹊徑，以某分布式風力機葉片為研究對象，針對其吸力面翼型曲線進行結構凹變，探究結構變化對風輪整體氣動性能和結構性能的影響特征，進而探索翼型凹變在葉片設計中應用的可行性。

近年來，翼型整體的優化設計方面的相關典型研究如：Grasso[1]開發了ECN-G1-21翼型，并利用縮比實驗進行了不同雷諾數時翼型氣動性能測試及失速分析；Mohamed[2]則針對達里厄風力機進行了新翼型設計；Wang[3]提出了一種考慮連續攻角變化的新的翼型設計方法，并提出了基于泰勒高階多項式的風力機專用新翼型設計方法[4]；Liu等[5]則開發了一種新的翼型結構參數化設計方法，并將其應用于DU93-W-210翼型的優化，進而佐證了該方法的先進性；Mei等[6]建立了一種專門針對于H型垂直軸風力機翼型的設計方法；Bedon等[7]利用優化的遺傳算法開發了一種翼型結構的改良方法；Tartuferi等[8]則開發了適用于Savonius風力機的專用新翼型；Birajdar等[9]開發了專門針對于小型風力機葉片設計的兩種新翼型IND 15045和IND 09848。

翼型局部的優化設計方面的相關研究如下：Menon等[10]進行了尾緣開槽對葉片氣動載荷的影響分析；Cai等[11]研究多種前緣突起對葉片氣動性能的影響，發現流體經過凹凸前緣時具有周期性和對稱性；Liu等[12]通過對葉尖結構進行凹槽設計，并利用PIV拍攝葉尖附近流場，發現葉尖開槽可以減弱葉尖渦的強度并加速耗散；Ahmed等[13]在不同雷諾數下在葉片前緣添加襟翼，發現前緣襟翼可以有效的增加小型風力機的氣動性能；Wang等[14]通過風洞試驗對DU40光滑翼型,DU40-llwavy和DU40-25wavy兩種仿生凹凸前緣翼型，進行流場測試發現，凹凸前緣能夠有效的延緩流動分離現象Hansen等[15]通過研究發現：凹凸前緣在葉片未失速時會提升翼型的升力系數，在失速狀態下，可以減小升力系數的損失；Sun等[16]設計一種新的后緣襟翼，可以有效的降低葉片根部的彎矩以及疲勞損傷。

綜合文獻分析可知，所見研究對葉片翼型的改良往往著眼于翼厚、翼型前/后緣點處結構優化改進為設計理念，專門針對于翼型中部曲線的優化研究較少，而利用該理念在設計工況下以不降低葉片功率輸出為前提的葉片結構動力學性能有效改進方法的相關研究則未見報道。

1 翼型結構凹變提出的理論依據

如圖1所示，風力機葉片旋轉過程中，因壓力面氣壓值高于吸力面，故各翼型面前、后緣點處均存在由壓力面流向吸力面的氣體環流，兩處環流最終于吸力面某處交匯，交匯的存在將導致葉面氣流能量損失的增加，并影響葉片運行的穩定性。本文通過合理選擇凹變位置、形式及幾何尺度可實現對交匯流線的引導及其影響范圍的限制，從而減小吸力面氣流的脈動及能量損失。基于上述分析，翼型凹變有可能不降低或在一定程度上提升葉片的做功能力；同時，翼型凹變將改變葉片外形結構及質量分布，故可在一定程度上改變葉片的剛度、阻尼比及其他結構參數，由此可獲得一種在不降低葉片氣動性能前提下其結構動力學性能有效改進的實現方法。

圖1 翼型吸力面流線的交匯Fig.1 Convergence of the flow line on the airfoil suction surface

2 翼型凹變的實現方法

以圖2(a)所示某翼型結構為例，假設翼型吸力面的繞流交匯線往往出現在距離前緣M處，選取該處為翼型向內側凹變的中心點。考慮到翼型弦長顯著大于厚度的結構特征，凹變結構對應選擇為橢圓面，令橢圓面中心點與凹變中心點重合，橢圓面長軸為A、短軸為B，并使橢圓面長軸與凹變中心點處翼型曲線相切，本例中橢圓面長軸與弦長的夾角α為2.25°，凹變翼面與非凹變翼面間采用B樣條曲線光滑過渡搭接，具體實現過程如圖2(b)所示。

(a)原翼型

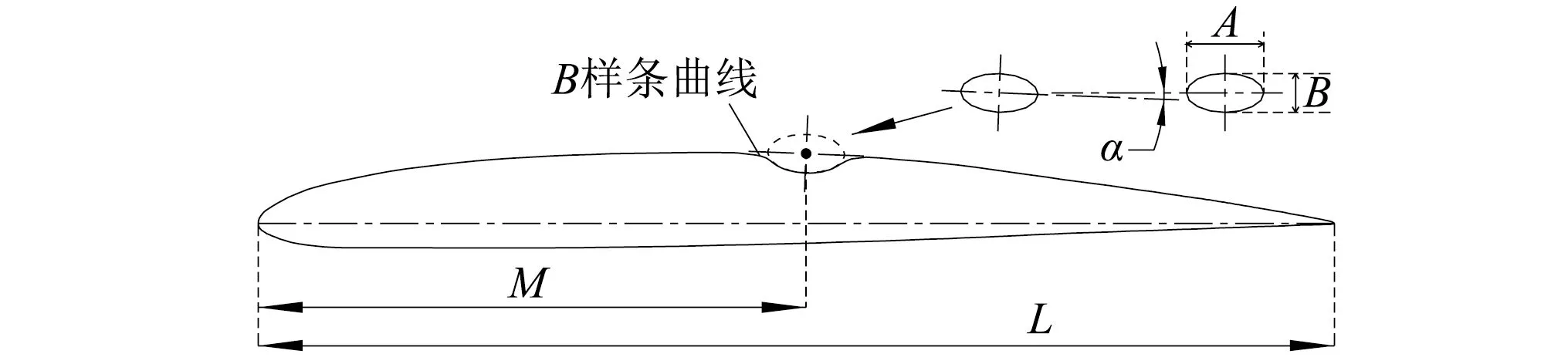
(b)凹變翼型L-翼型弦長;M-翼型曲線上凹變中心點到翼型前緣的距離;A-橢圓面長軸長;B-橢圓面短軸長圖2 翼型凹變原理Fig.2 Principle of airfoil concave

3 翼型凹變對風輪氣動性能的影響

3.1 數值仿真模型的建立

3.1.1 凹變翼型葉片的生成原理

葉片為木質實心結構，長為0.7 m，葉片翼型部分設置有10特征翼型面，各翼型面之間的部分通過放樣實現，1翼型面和2翼型面的間距為35 mm，其余相鄰翼型面間距為70 mm。將原翼型中的10特征翼型面曲線進行相應的結構凹變并放樣后即可獲得凹變翼型葉片，如圖3所示。

圖3 凹變翼型葉片的生成Fig.3 Generation of concave blades

3.1.2 計算模型的建立

數學模型依據內蒙古自治區新能源試驗示范基地所屬B1/K2型低速風洞建立，如圖4所示，目的是利用相應的試驗佐證算法的可靠性。

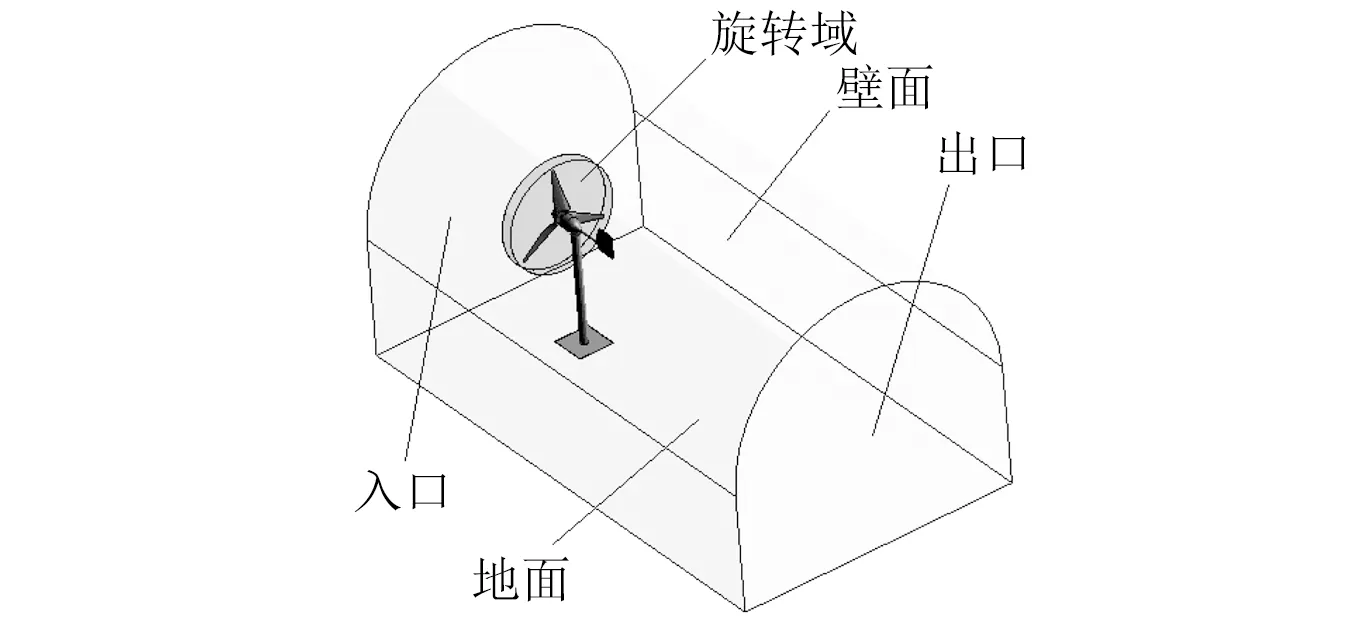
圖4 數學仿真模型Fig.4 Mathematical simulation model

計算域劃分為旋轉域和靜止域兩部分，旋轉域包裹風力機葉片，通過域的旋轉實現葉片的轉動。旋轉域采用六面體網格，靜止域采用四面體網格，兩域間采用滑移網格，數據傳遞采用INTERFACE技術。靜止域采用網格膨脹技術，全域實現了網格的分層劃分，多種網格劃分技術的綜合應用可實現計算資源的高效利用。

3.1.3 計算方法及結果分析

采用非穩態算法，考慮到葉片旋轉過程中，伴隨著較強的逆壓梯度和流動分離，故所采用算法模型需考慮湍流剪切應力效應，并對渦流黏度不產生過度預測，SSTk-ω湍流模型在上述問題解決方面具備顯著的優勢。且壁面采用固體無滑移條件，入口條件采用速度入口，出口條件采用自由出口，網格間數據的傳遞采用二階差分格式。

原翼型葉片額定風速為10 m/s，設計尖速比為5，針對此工況進行原翼型風輪氣動性能的計算，如表1所示。

表1 原翼型風輪氣動性能Tab.1 Aerodynamic performance of 3 types of wind wheels

3.2 葉片氣動性能可靠性試驗

3.2.1 測試對象

測試對象，如圖5所示，為與模擬計算使用相同葉片的某木質葉片表面涂有玻璃鋼材料，輪轂采用法蘭連接。

圖5 葉片實拍圖Fig.5 Pictures of physical blades

3.2.2 測試方法

通過吹氣式B1/K2低速風洞提供穩定來留風速，風輪電機輸出端與負載系統和NORMA5000 型功率分析儀設備連接，以此獲取風力機的功率參數如圖6所示。

圖6 功率監測方法Fig.6 Power monitoring method

3.2.3 測試結果

實驗結果如表2所示，定義相對誤差=(計算值-實驗值)/實驗值×100%。

表2 實驗功率與模擬功率對比Tab.2 Comparison of experimental power and analog power

由表2可知，模擬計算功率與實驗功率在風輪的設計工況下功率相對誤差為4.7%，因此模擬計算具有較高的可信性。

3.3 翼型凹變幾何參數的確定

一方面，經過模擬計算后發現，翼型凹變過淺，對葉片吸力面流線的控制不明顯，而凹變過深，則會使葉片凹變處過薄，增加了斷裂的風險。通過模擬計算后，測得當橢圓長軸A為弦長C的6.3%、短軸B為翼型弦長C的1.5%時，該凹變形狀對于流線控制較強，而且不會使得凹變處過薄，則選取該形狀參數為本文凹變形狀。另一方面，在設計工況下,葉片吸力面流線交匯，一般出現在葉片吸力面0.7～0.9倍弦長處，因此，選取翼型0.7倍、0.8倍、0.9倍弦長處進行凹變。同時，為了使得，凹變葉片能夠對其結構性能產生一定程度的影響，綜合考慮之下選取凹變長度為350 mm和420 mm兩個長度最為適宜。進而通過模擬計算后得出，原翼型風輪與不同凹變翼型風輪在設計工況下的氣動性能，如表3所示。

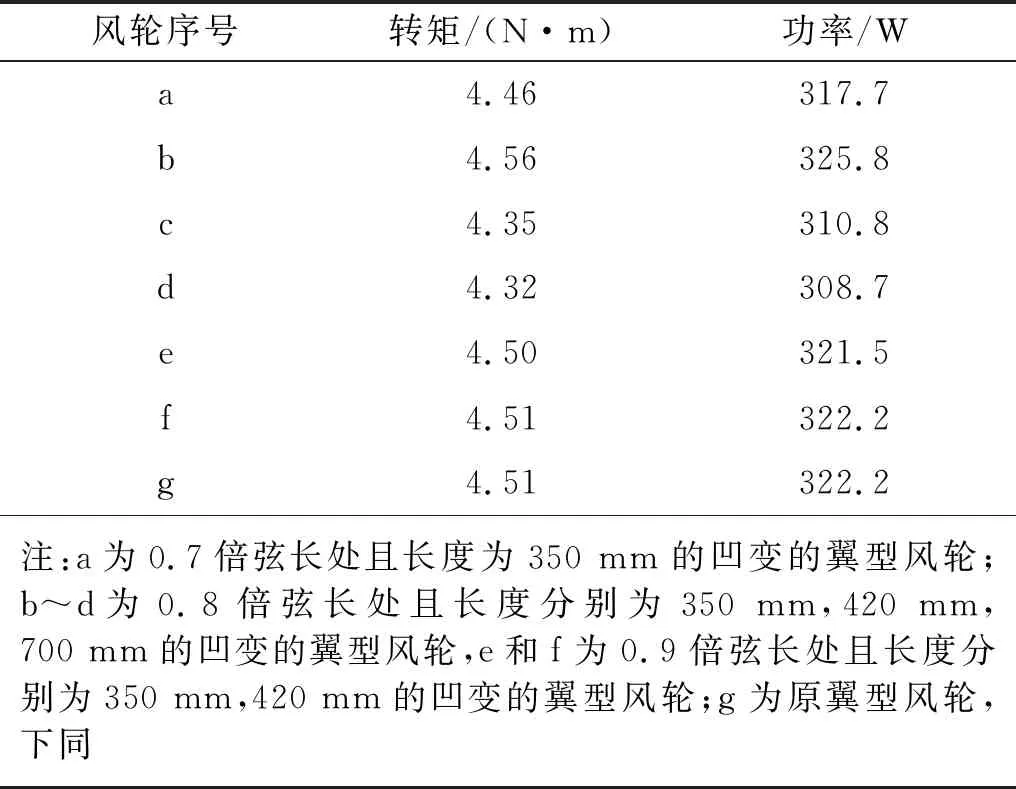
表3 a～g風輪氣動性能Tab.3 Aerodynamic performance of a～g wind turbine

由表3中數據可知，設計工況下，b類風輪轉矩較原翼型風輪略有增大，分析其原因為：翼型向內側凹變后，吸力面的交匯流線規則地沿凹槽發生流動，較好地限制了交匯流線隨工況變化于葉片位置的遷移，如圖7所示；同時，翼型向內側凹變，一定程度上限制了流線交匯處湍流的擴散，減小了吸力面氣體的流動能量損失。因此，也可認為b類風輪相較于其它凹變風輪，對于流線的控制更為優異，使得其功率較原風輪有1%的提高。較好地實現了翼型凹變對葉片氣動性能微影響的設計初衷。

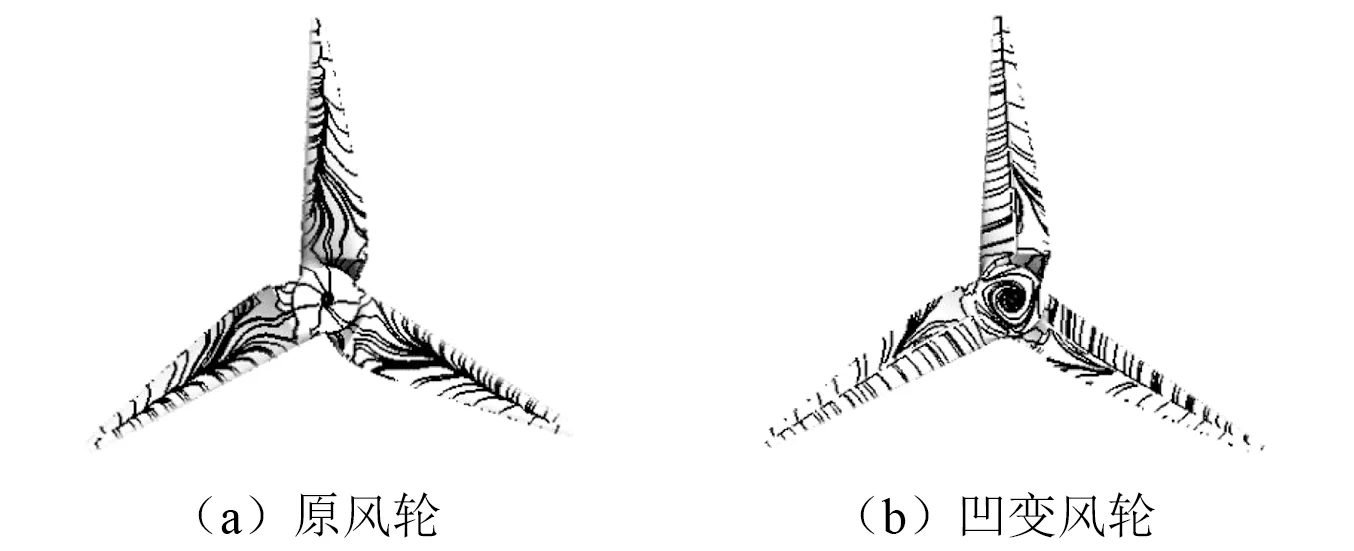
圖7 凹變葉片對吸力面流線交匯的控制Fig.7 The control of the confluence of a concave blade on the streamline of the suction surface

同時，為了探究在翼型其它弦長處進行凹變，是否對葉片的氣動性能的提高有更好的影響。進而嘗試在葉片的0.2～0.6倍弦長處進行長度為350 mm的凹變，并進行模擬計算獲得其轉矩值如表4所示。

由表4可知在翼型0.2～0.6倍弦長處進行凹變后，1～6類風輪轉矩有顯著的降低。對風力機的氣動性能降低影響較大。因此下文主要對a～f類凹變風輪進行結構動力學性能的模擬與實驗。

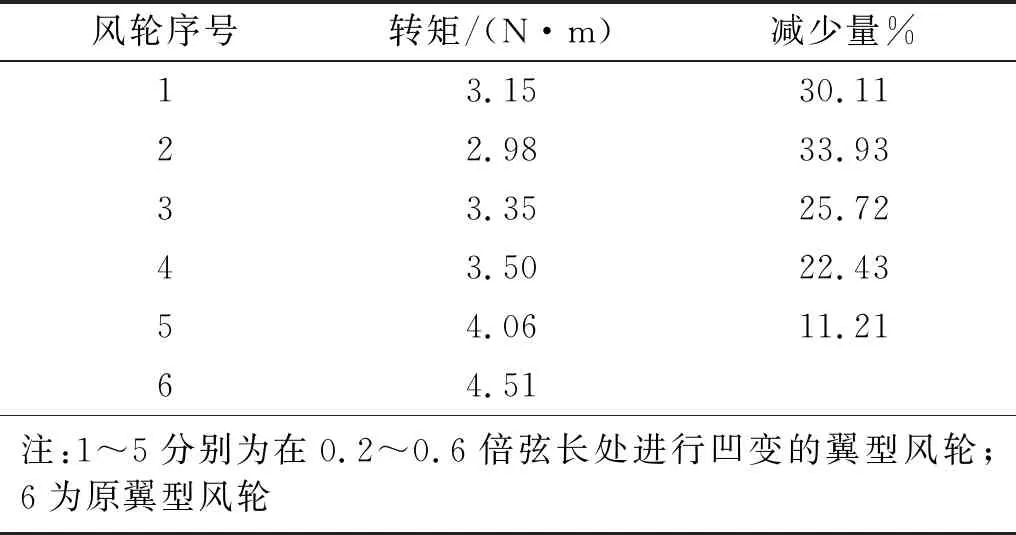
表4 1～6類風輪氣動性能對比Tab.4 Aerodynamic performance of wind wheels

4 翼型凹變對葉片結構動力學性能的影響

4.1 翼型凹變對葉片剛度的影響

4.1.1 測試對象及傳感器布置

測試對象為課題組某木質原葉片與b類凹變葉片，如圖8所示，其翼型與模擬計算相同，表面涂有玻璃鋼材料，輪轂采用法蘭連接。

圖8 b類凹變葉片與傳感器布置Fig.8 Pictures of physical blades and arrangement of sensors

4.1.2 測試系統、測試原理及方法

測試系統采用 B &K 公司最新研發的PULSE16.1結構振動分析系統。測試原理如圖9所示。

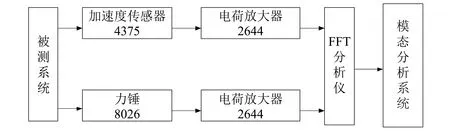
圖9 模態測試原理Fig.9 Principle of modal test

測試方法采用瞬態激振法，單點激勵，多點響應。激勵信號由力錘人工施加，力錘所產生的激勵信號由其手柄處的數據線傳輸給數據采集卡;葉片產生振動后，由加速度傳感器感知測點處的振動信息，并由數據線傳輸給數據采集卡;數據采集卡收集數據，并對數據進行相關處理后，通過網線傳輸給電腦中的 Pulse 系統控制程序;控制程序完成測試系統的整體設置、控制及測試數據的顯示、保存等功能。

4.1.3 測試結果分析

將數據導出到Reflect中進行后處理分析得到g類葉片與b類凹變葉片在一階、二階的振動頻率及對應的阻尼比，如表5所示。

表5 不同風輪振動頻率及阻尼比Tab.5 Vibration frequency and damping ratio of different wind turbines

從表5中可以明顯看出b類葉片相較于與g類葉片在，一階、二階固有頻率有2%和1%的增加、阻尼比有9.22%和3.4%的增加。分析其原因：當葉片被力錘敲擊時的振動形式，可以看做為一個單自由度有阻尼的振動形式。

則葉片靜剛度

(1)

式中：f為固有頻率；k,m為剛度與質量；ζ為阻尼比。

通過承重得到，b類葉片較與g類葉片質量減少為Δm=8 g(減少量為1%)，進而將其與階頻率及阻尼比代入公式，計算得到b類凹變葉片與原葉片的剛度差Δk的增量為32%，由此可得，b類凹變葉片能夠有效的增加葉片的靜剛度。

同時，由于風輪在實際工況運行下是動態的，所以計算葉片的動剛度，才能真實的反應出葉片在運行工況下的剛度變化。

其運動方程為

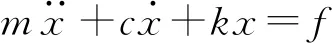
(2)

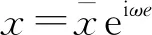
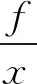
(3)

則動剛度

K=k-mω2+ciω

(4)

式中:k為靜剛度；m為質量；ω為風輪旋轉角速度；c為阻尼系數。

通過靜載試驗計算出物體靜剛度增加量為32%，則在設計工況下，根據公式推導出凹變翼型葉片的動剛度也有很大程度的增加。

綜合靜剛度與動剛度的變化發現，凹變葉片一階、二階阻尼比的上升使得葉片振動消減速度變快，相同工況下對葉片的疲勞損失也會有很大程度的下降。同時，由于小型水平軸風力機的主要運行工況頻率多發生在葉片一階與二階固有頻率左右，凹變葉片在一階、二階振動頻率上的提高，使得運行工況偏開葉片固有頻率，減少斷裂的風險。

4.2 翼型凹變對葉片最大位移及應變的影響

由于風輪葉片為實體木質，剛度較大，算法可以采用單向流固耦合計算。首先通過流場計算，得到風壓載荷，進而將氣動力、離心力、重力等加載到風力機，進行有預應力的結構場計算，最后得到葉尖位移與應變的大小。以a類風輪為例，通過模擬計算，求得葉片位移與應變振型，求得具體參數如表6所示。

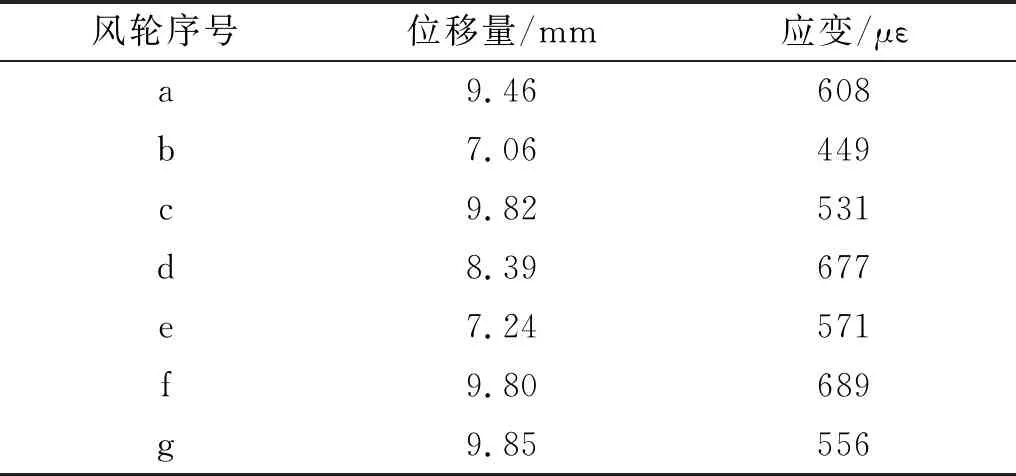
表6 葉尖位移及應變量值Tab.6 Tip displacement of single leaf blade

由表6可知，b類凹變葉片，相較于其它葉片最大位移以及應變減少量最為顯著，分別為28%和19%。分析原因：一方面，通過上文實驗驗證，翼型凹變后葉片剛度相較于原葉片很大程度的提高，同時，剛度提高使得葉片在外力作用下產生的彈性變形降低；另一方面，翼型凹變能在一定程度上限制了流線交匯處湍流的擴散，減小了吸力面氣體的流動能量損失，使得吸力面湍流度降低，即對于葉片的擾動下降。綜上兩個因素，可以較好的解釋葉片最大位移及應變有顯著的下降的原因。

4.3 模擬計算結果的驗證

由于實驗條件所限，無法在實驗中直接測得葉尖最大位移的具體數值。本文為驗證上述模擬計算結果的可靠性，進而對b類葉片與g類葉片，進行葉片應變的動態風洞實驗。以此從側面驗證模擬計算的可靠性。

4.3.1 測試設備原理及測點分布

應變值采集裝置采用旋轉機械應力應變遙測分析系統 TST5925測試原理，如圖 10 所示，該系統為國內首臺專門針對風力機葉片動態應力應變信號采集設計的裝置。

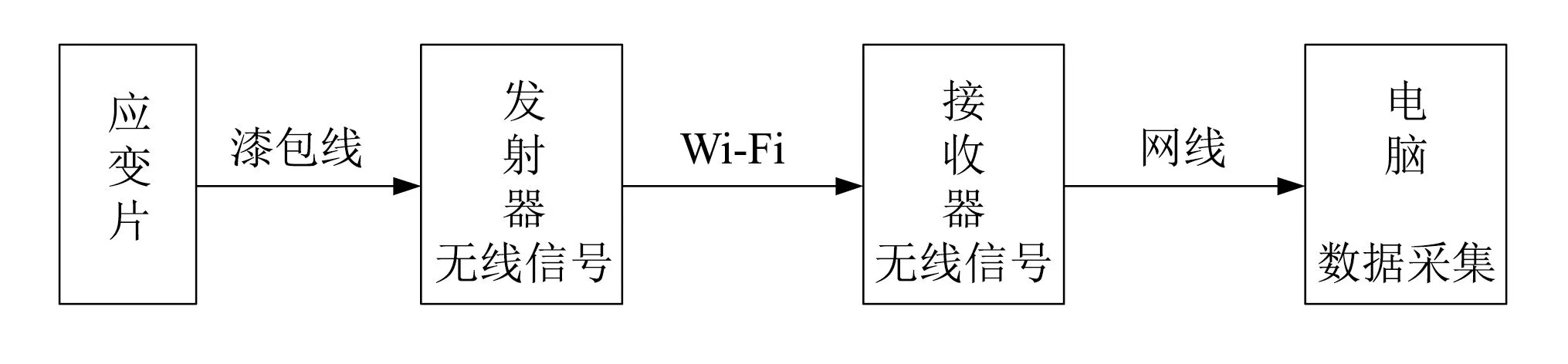
圖10 應變值測試原理Fig.10 Principle of strain measurement

通過模擬計算觀察發現葉片應變最大值，出現在葉跟0.17R處，即1號、8號、9號附近，并將其作為主要測試位置。葉片三階以下振型的節點位于距風輪旋轉中心處0.27R,0.51R,0.74R,0.85R，振幅較大，作為此次動態應變試驗的輔助測試位置，如圖11所示為應變片位于葉片迎風面與背風面的分布情況。

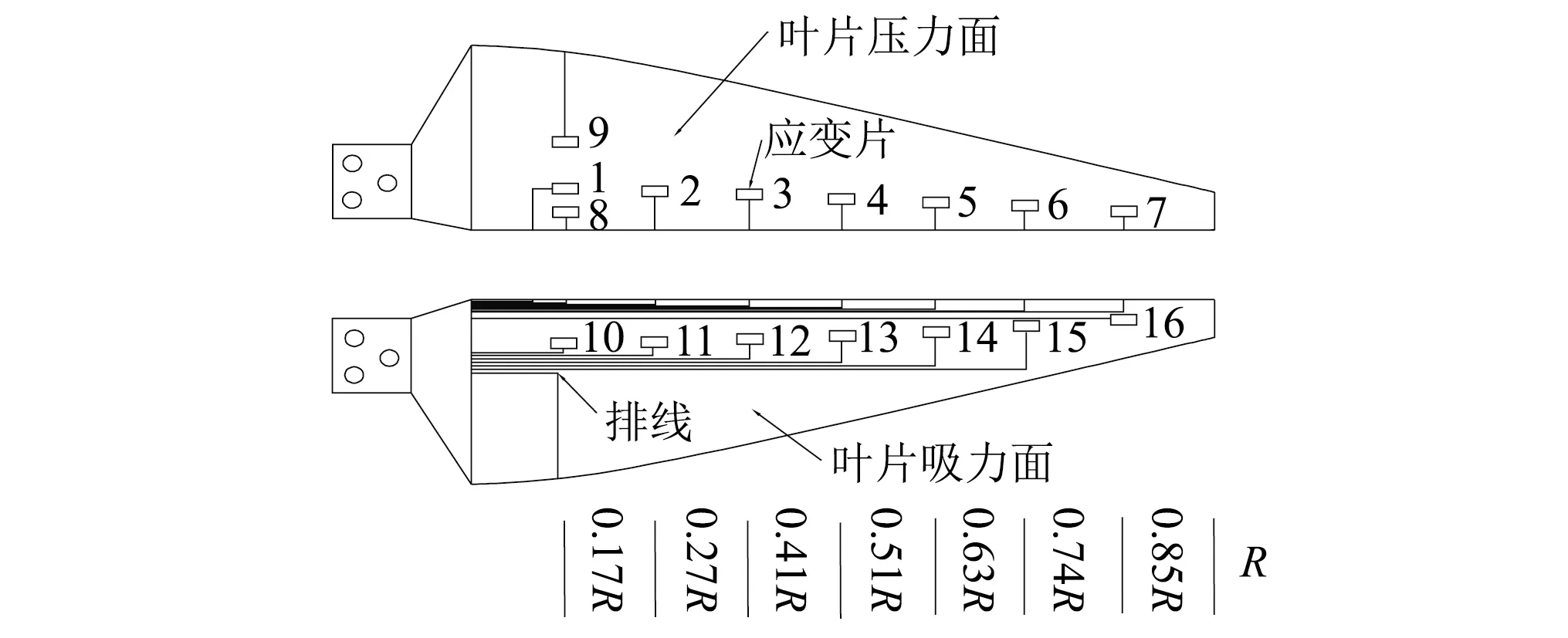
圖11 應變測點分布Fig.11 Measuring-point distribution of strain

4.3.2 應變響應信號測試結果分析

通過試驗測試得出，葉片最大應變值出現在葉跟處的1號測點，這與模擬計算結果的位置保持一致。則1號測點的實驗結果如表7所示，定義相對誤差=(計算值-實驗值)/實驗值×100%。

表7 1號測點實驗與模擬應變對比Tab.7 Comparison of 1 point test and simulated strain

由表7知，設計工況下功率相對誤差為3.7%與4.2%，較好的驗證了上述模擬計算方法的可靠性。進而得出：翼型凹變葉片可以有效的減少葉片的最大位移及應變值，增加葉片的結構動力學性能。

5 結 論

針對某分布式水平軸風力機葉片開展翼型凹變的結構改進，本文首次提出于翼型吸力面上進行結構改形的探索，發現通過合理選擇凹變位置、形式及幾何尺度，可在一定程度提升葉片做功能力、提高風輪一階、二階固有頻率及其阻尼比，并提升葉片靜剛度與動剛度，進而減小葉片的應變值，使得葉片在外力作用下產生的彈性形變有顯著的下降。翼型凹變的成功實現，不僅為風力機葉片翼型族的開發提供了新方法，同時可為諸多氣動性能優異的風力機葉片在遠短于設計壽命期內頻發疲勞損傷事故而導致的產品夭折提供新的解決思路。

另一方面，本文所建立翼型凹變的方法，應可以成功地引用到大型風力機葉片設計，大型風力機葉片均采用中空的鋪層結構，由理論分析可知，本文所提到的翼型凹變方式對大型風力機而言，均可一定程度上增強葉片的剛度，提高其固有振動頻率，進而實現整機避振的結構改良。