應用混合單元基光滑點插值法的聲固耦合分析

陳澤聰，陳毓珍，何智成，張桂勇,4,5，王海英

(1．大連理工大學 船舶工程學院 遼寧省深海浮動結構工程實驗室，遼寧 大連 116024；2.中國船舶工業集團 上海船舶研究設計院，上海 201203；3.湖南大學 汽車車身先進設計制造國家重點實驗室，長沙 410082；4．大連理工大學 工業裝備與結構分析國家重點實驗室，遼寧 大連 116024；5.高新船舶與深海開發裝備協同創新中心，上海 200240；6.大連海洋大學 航海與船舶工程學院，遼寧 大連 116023)

結構在受到載荷激勵的時候，會產生振動，同時通過壓縮附近的流體介質向周圍聲場輻射噪聲，而聲場聲壓的變化反過來又會激勵結構的振動，形成結構與聲學介質相互作用的結構聲振耦合系統。在汽車、船舶和飛機等結構體的振動噪聲分析中，基本都涉及到結構和聲學介質的相互作用，所以聲固耦合系統的研究一直是振動與噪聲控制領域的研究熱點之一。高效精準地預測耦合系統的結構和聲場響應有著十分重要的意義，不但可以為結構件的設計優化提供依據，而且對系統采取的減振降噪措施具有指導性作用。

結構聲振耦合系統的數值模擬包括結構、聲場和它們之間的相互作用。Gladwell等[1]最早建立了基于不同場變量如位移或力相關量的聲固耦合理論公式，并進行薄板與空氣的聲振耦合分析。Craggs[2]詳細推導了混合變量(結構采用位移變量而聲場采用聲壓變量)聲固耦合系統的有限元方程，使有限元法(Finite Element Method,FEM)逐漸成為解決聲固耦合問題的重要手段。但因為有限元法[3]是對全域進行離散，所以主要應用于有界聲場的聲固耦合分析，且由于其矩陣的稀疏性，相比邊界元計算內聲場效率較高。針對無界聲場問題，一般采用邊界元法(Boundary Element Method,BEM)[4]進行模擬，它只需要對聲場的邊界進行離散，并且自動滿足無窮遠處的Sommerfeld輻射邊界條件，在結構聲輻射等外聲場問題中具有明顯的優勢。目前，Nastran、LMS Virtual.Lab Acoustics等常用商業軟件的結構聲場耦合分析主要采用的就是有限元/有限元耦合法(FEM/FEM)[5-7]和有限元/邊界元耦合法(FEM/BEM)[8-10]。在滿足聲學經驗法則[11](一個波長范圍內至少要有6個線性單元)的前提下，這兩種方法在低頻的結構聲振耦合數值模擬中都能得到很好的結果。但隨著頻率的升高，色散誤差逐漸增大并占據主導地位；其根本原因是有限元法和邊界元法形成的系統剛度偏硬，導致計算的聲音傳播速度比實際聲速快，從而給數值計算帶來較大誤差。通過減小單元尺寸可以在一定程度上抑制色散誤差，但同時會帶來巨大的計算時間代價。

近年來Liu等[12]提出了基于廣義梯度光滑技術的光滑有限元法(Smoothed Finite Element Method,SFEM)和光滑點插值法(Smoothed Point Interpolation Method,SPIM)[13]。理論證明及大量的數值算例說明光滑方法能夠有效地軟化系統剛度，從而提高結構和聲場的計算精度。姚凌云等[14]將二維光滑有限元應用到聲固耦合分析的結構域中，提出了光滑有限元/有限元耦合法(SFEM/FEM)，得到了比FEM/FEM更高的精度，但沒有對聲學單元進行光滑處理。何智成等[15]構建了三維邊光滑有限元(Edge-Based Smoothed Tetrahedron Finite Element Method,ES-T-FEM)來計算結構聲振耦合中的流體域，結合二維邊基光滑有限元(Edge-based Smoothed-FEM,ESFEM)的Mindlin板單元進行耦合分析，其計算精度甚至超過了改進的六面體單元。為了得到無限接近連續系統的剛度，Li等[16]還通過混合光滑有限元方法(HS(Hybrid Smoothed)FEM)(點基光滑有限元(NS(Node-based Smoothed)FEM)與線性有限元的結合)來分別逼近結構和聲場的系統剛度，并進行結構聲場響應分析，得到的結果與參考解非常吻合。但是，ESFEM和NSFEM都需要重新構造光滑域來進行梯度光滑處理。

本文將Liu等[17]提出的混合單元基光滑點插值法(CSαPIM)應用于聲場的數值模擬，結合邊基光滑有限元(ESFEM)的板單元[18]，對系統進行結構聲振耦合分析。與ESFEM和HSFEM相比，由于基于單元的光滑點插值法(Cell-based Smoothed Point Interpolation Method,CSPIM)的光滑域和背景單元重合，因此在形成混合單元基光滑點插值法(CSαPIM)時不需要在背景網格的基礎上生成局部光滑域，計算形狀函數時只需要在徑向基函數形函數基礎上以一定權重加上線性有限元對應節點的形函數即可。而且，由于線性有限元采用線性插值方式，在邊界面上的3個節點形函數為一定值1/3，使得計算過程更加方便高效。在此聲固耦合系統中，結構采用二維三角形板網格，聲場采用三維四面體網格，可以很好地適應任意復雜幾何模型，減少前處理的工作量。同時，由于計算精度的提高，尤其是針對較高頻率的色散誤差具有明顯的抑制作用，在相同尺寸的網格下，可計算的頻率范圍更寬，具有極大的工程實用意義。

1 構造基于ESFEM的Mindlin板單元

板結構在汽車、船舶和飛機等交通工具的艙室中應用廣泛，研究板結構與聲場的耦合作用具有十分重要的工程意義。此處采用二維的三角形Mindlin板單元來模擬結構域，無阻尼板結構振動的離散方程可寫為

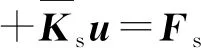
(1)

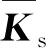
(2)

(3)

(4)

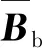
為了消除Mindlin板單元的剪切自鎖現象，這里引入離散剪切間隙法(Discrete Shear Gap,DSG)[19]來處理單元的剪切剛度，從而提高計算精度。在應用DSG的板單元中，彎曲應變εb和剪切應變εs可分別寫為

εb=Bbue;εs=Bsue

(5)

式中：ue為單元位移向量；Bb和Bs分別為單元的彎曲應變矩陣和剪切應變矩陣。

邊光滑有限元已被大量數值算例[20]證明剛度與連續系統非常接近，相比有限元，在同一網格下能夠更加準確地模擬結構動力學問題。邊光滑指的是構造基于邊的光滑域并對其進行應變光滑操作，具體過程如下。

首先利用商業軟件自動生成三角形網格作為背景網格，如圖1所示。基于三角形的每條邊構造光滑域：若邊在計算域的內部，則由該邊的兩端點和共享該邊的兩個單元的形心點作為頂點形成光滑域；若邊在問題域的邊界，則由該邊的兩端點和其所在單元的形心點作為頂點形成光滑域。

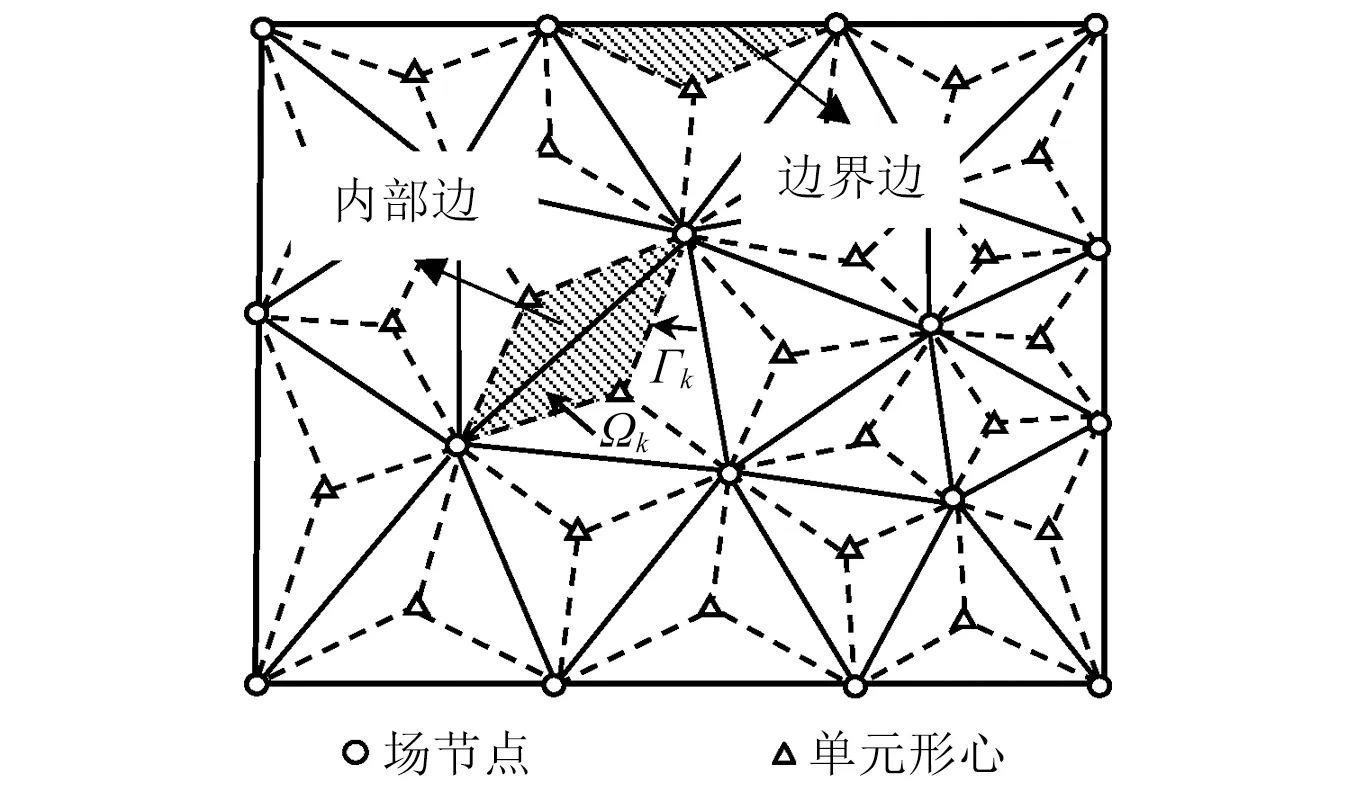
圖1 基于三角形網格以邊為中心的光滑域Fig.1 Edge-based smoothing domain based on triangular meshes

在形成線性有限元的單元應變矩陣的基礎上，對光滑域進行應變光滑操作，表達式為

(6)

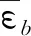
(7)

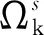
(8)

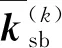
(9)

2 構造基于CSαPIM的聲學單元

在理想流體介質和小振幅聲波的假設下，無損耗聲波方程的離散形式可以描述為

(10)

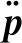
(11)

(12)

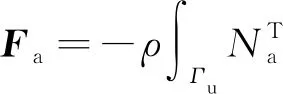
(13)

2.1 濃縮的RPIM形函數

本文將聲場域離散成四面體網格，采用混合單元基光滑點插值法(CSαPIM)來進行數值模擬，并通過調整權重參數α∈[0,1]得到與連續系統非常接近的剛度，從而提高聲學計算的精度。下面介紹剛度偏軟的引入虛擬節點的單元基光滑點插值法(CSRPIM-T5-Cd)的光滑應變構造過程。

在單元基光滑點插值法(CSPIM)中，采用的是基于面的選點模式：對聲場域邊界上的面采用面的3個頂點(T3形式)進行線性插值，而對聲場域內部的面采用面的3個頂點加上共享該面的兩個單元的另外兩個頂點作為插值點(T5形式)，如圖2所示。

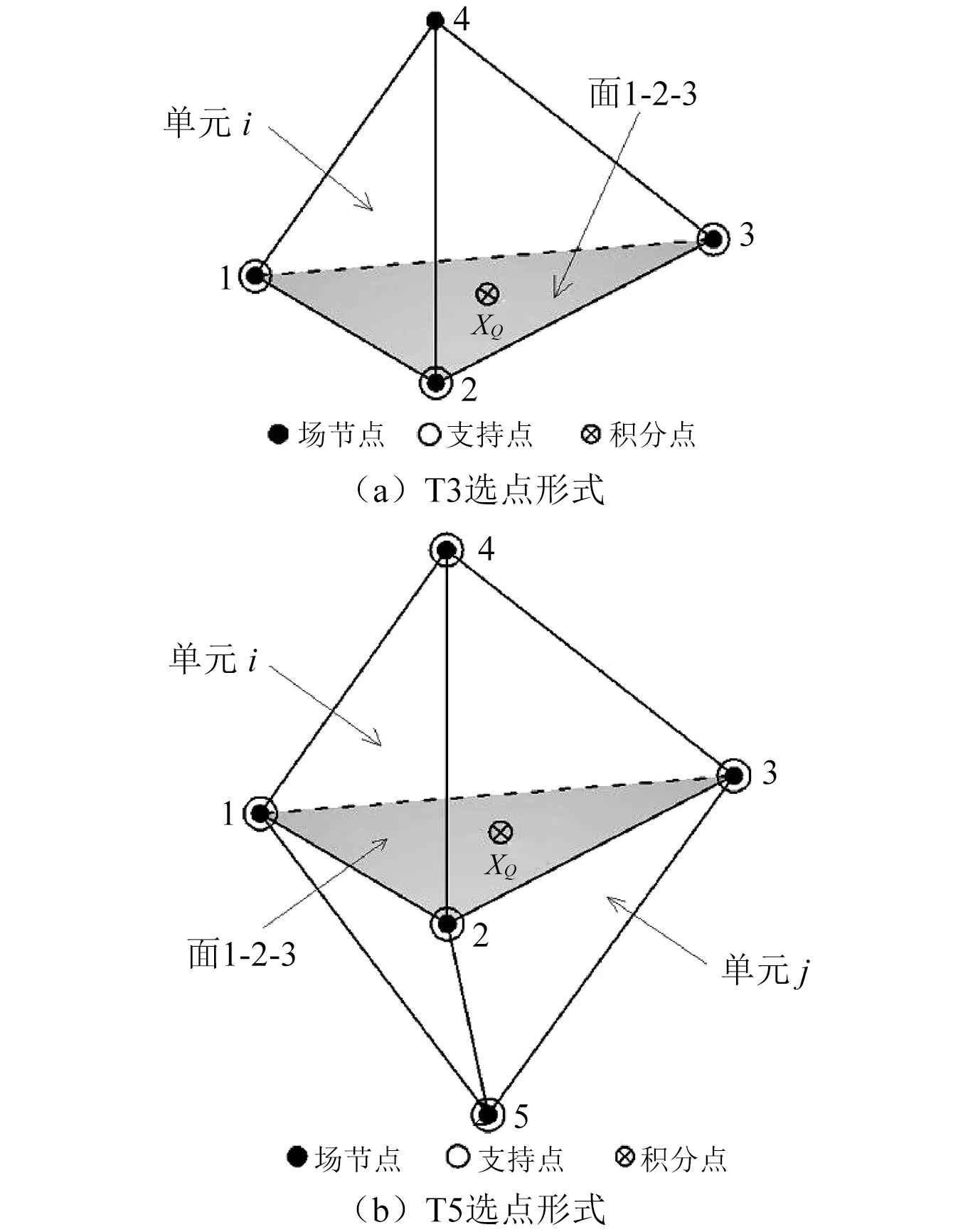
圖2 基于面的選點模式Fig.2 Face-based schemes for selecting support nodes

為避免采用多項式基PIM引起的奇異性問題，本文采用徑向基函數(Radial Basis Function,RBF)作為插值形式，它的另一個好處是插值精度高，同時方便支持點的靈活選取。另外，為了滿足徑向基(Radial Point Interpolation Method,RPIM)的線性再生性，一般會添加一次完全多項式基以改善其性能，確保RPIM能通過標準分片試驗。添加PIM(Point Interpolation Method)的RPIM插值形式可表示為

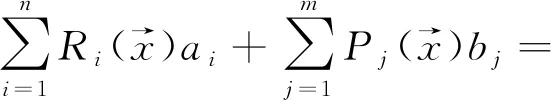
(14)

式中:Ri和ai分別為徑向基及其系數；Pj和bj分別為多項式基及其系數；n為局部域的支持點數目；m為多項式基數目，此處取線性完全多項式，即m=4。他們的向量形式可以表示為

aT={a1,a2,…,an};bT={b1,b2，…，bm}

(15)

(16)

(17)

這里選擇復合二次形式(MQ-RBF)作為徑向基函數，形狀參數αc，q采用書中的推薦值。

(18)

式中：ri為支持點i和被插值點的徑向距離；dc為問題域內節點的平均間距。使式(14)滿足計算點x周圍的n個節點值，可以得到n個線性方程，即

(k=1,2,…,n)

(19)

矩陣形式可表示為

ds=RQa+Pmb

(20)

式中：ds為函數值向量；RQ和Pm分別為徑向式和多項式的力矩矩陣。

由于式(20)中有n+m個變量，需添加下面m個約束條件作為附加方程方可求解。

(21)

聯立式(20)和式(21)，最后可以得到對應于n個節點位移向量的RPIM形函數可表示為

(22)

在T5形式的基礎上，引入6個虛擬節點，其位置分別取在T5單元6個面的形心上，如圖3所示。坐標值可通過下式求得

(23)

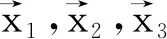
通過5個真實節點(1～5)和6個虛擬節點(6～11)，共11個支持點進行插值，我們可以得到濃縮前的RPIM形函數

(24)

(25)

為了消去虛擬節點的位移，我們假定虛擬節點的位移與所在面的3個頂點位移具有線性關系，即

(26)

將式(26)代入式(25)，可以得到

(27)

式中：濃縮后的RPIM形函數可為如下形式

(28)

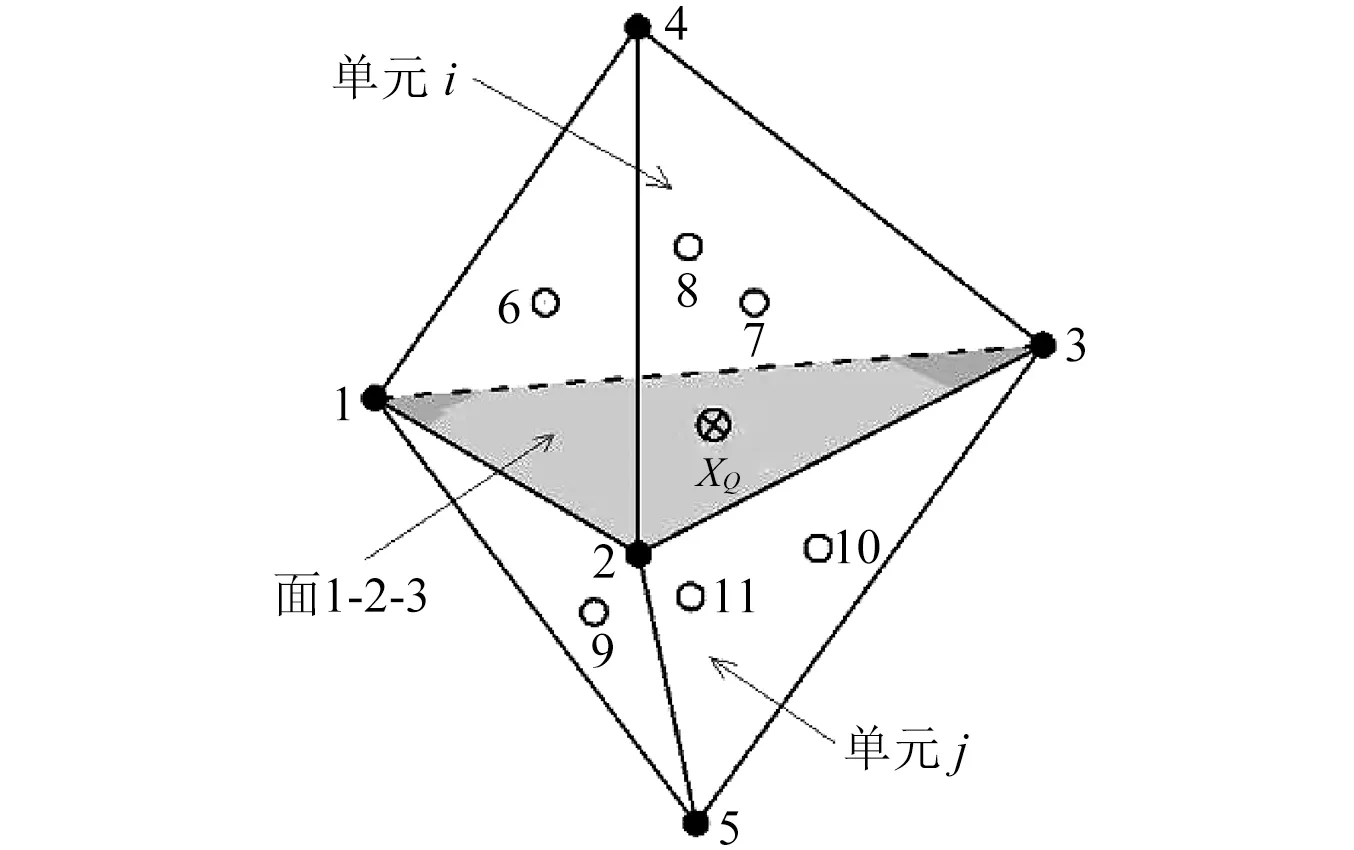
圖3 引入虛擬節點的T5選點模式Fig.3 T5 scheme with virtual nodes for selecting support nodes

2.2 混合單元基光滑點插值法

混合單元基光滑點插值法是指在形成局部域形函數時將剛度偏軟的CSRPIM-T5-Cd和剛度偏硬的FEM以一定權數相加并保證權數之和為1，通過改變權數的值來調節離散系統的剛度。當α取合適值時，不但收斂性和計算精度能得到有效提高，而且在畸變網格下也能得到合理的結果。同時，由于單元基光滑點插值方法的光滑域和背景網格重合，所以不需要構造光滑域的步驟，可以節省前處理時間。應用廣義梯度光滑技術，我們把原來的梯度替換為光滑梯度，并通過格林公式將域積分轉變為邊界積分，可描述為以下形式

(29)

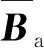
(30)

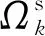
由于FEM相當于單元基光滑點插值法的一種特殊形式，表現為在光滑域的面上采用線性插值形式，也就是說，它在3個頂點上的形函數為一定值1/3，因此不需要額外的計算，只需要在CSRPIM-T5-Cd積分求和得到形函數后直接以不同權重相加即可，如下

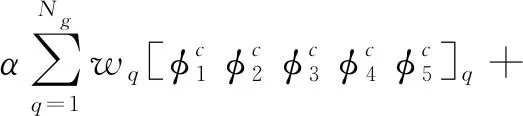
(31)

式中：α∈[0,1]為權重參數；Ng為CSRPIM-T5-Cd的邊界面積分選擇的高斯積分點數目；wq代表第q個積分點的權數。

最后生成每個光滑域的局部剛度矩陣，并組裝成總剛度陣

(32)

(33)

3 結構-聲場耦合方程

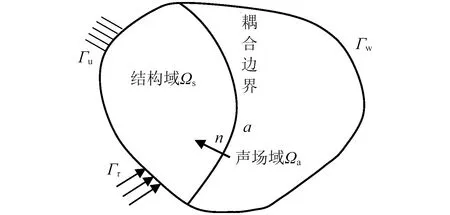
圖4 結構-聲場耦合模型示意圖Fig.4 Sketch of structural-acoustic coupling model

(34)

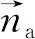
根據式(13)可以得到，結構在耦合界面?Ωsa對聲場的作用載荷為

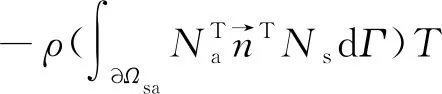
(35)

式中：Na和Ns分別為聲場和結構的形函數，這里用的都是線性三角形的形函數；T為將廣義位移向量轉變為線位移向量的轉換矩陣。

(36)

根據式(4)可以得到，聲場在耦合界面?Ωsa對結構的作用載荷為

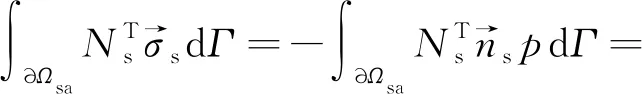
(37)

聯立式(1)、式(10)、式(35)、式(37)，可以得到時域下無阻尼結構-聲場耦合系統的控制方程

(38)

式中：H為耦合矩陣，表達式為

(39)

假設位移和聲壓均為簡諧波函數，則基于頻域的結構和聲場耦合的強迫響應可以表示為

(40)

4 確定α的取值

本節利用一個具有解析解的聲學問題來確定α的取值，通過調節α的值來改變離散系統的剛度，達到接近連續系統的剛度，以提高聲學計算的精度。問題域如圖5所示，長度為1 m，寬和高均為0.1 m，左邊界施加簡諧速度激勵，右邊為完全吸聲邊界。域中介質為空氣，密度ρ為1.225 kg/m3，聲速c為340 m/s。精確解的表達式為

p=ρcvncos(kx)-jρcvnsin(kx)

v=vncos(kx)-jvnsin(kx)

(41)

圖5 問題域示意圖Fig.5 Schematic of problem domain

根據聲學經驗法則，想要得到可信賴的計算結果，一個波長范圍內至少要包括6個線性單元，即波數k和單元尺寸h應滿足kh=1的關系。本文在保證kh=1的基礎上，選取尺寸分別為0.1 m，0.05 m，0.025 m(對應頻率分別為541 Hz，1 082 Hz，2 164 Hz)的三套網格對上述問題進行數值模擬。不同網格全局誤差隨α變化的曲線，如圖6所示。

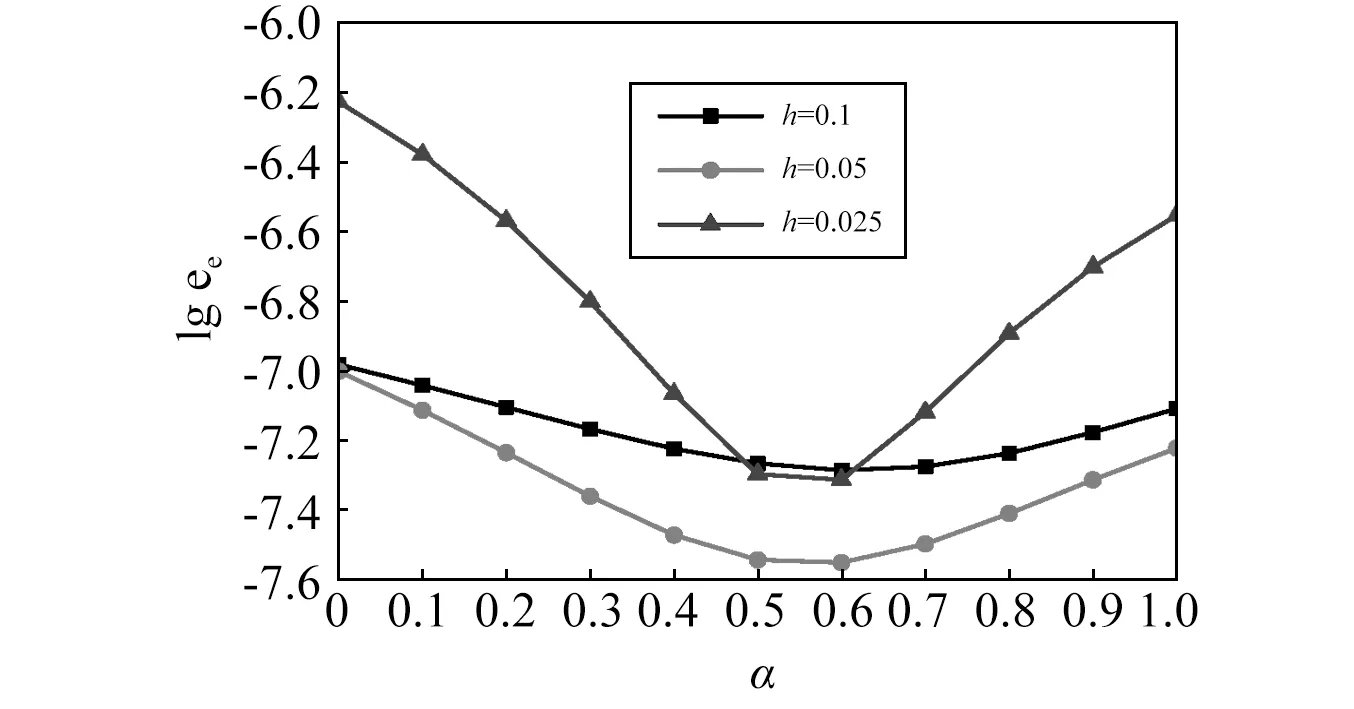
圖6 不同α值下的全局誤差Fig.6 Global error varying with different α values

其中，全局誤差可定義為

(42)

從圖6可知，在保證kh為常數的前提下，網格尺寸越細，對應計算頻率越高;前者在固定頻率下會提高計算精度，后者在固定網格尺寸情況下由于色散誤差會降低精度。而當網格較粗時，因為內部單元面較少，形成CSαPIM的形函數所占比例少，所以全局誤差變化不明顯。但值得注意的是，針對所研究的三種網格形式，當α∈[0.5,0.6]時計算精度一致較高，尤其當α=0.6時，全局誤差最小。因此，在下文的聲振耦合數值模擬中，基于CSαPIM的聲學單元統一取α=0.6進行計算。

5 數值算例

5.1 特征值預測

圖7為二維柔性板與三維聲場的耦合模型，其中聲場域尺寸為0.6 m×0.5 m×0.4 m，上表面為與板的耦合面，其他表面為剛性壁面；板的四邊為簡支邊界，尺寸為0.6 m×0.5 m。聲場媒質為空氣，密度ρa=1.225 kg/m3，聲速c=340 m/s。板的材料為鋁，參數如下：彈性模量E=71 GPa，密度ρs=2 700 kg/m3，泊松比ν=0.3，厚度t=0.005 m。

圖7 柔性板與聲腔耦合模型Fig.7 Flexible plate coupled with acoustic cavity

結構聲振耦合系統的計算精度不僅和聲場的計算方法有關，還和結構的計算方法有關。本節分別采用FEM/FEM耦合法，FEM/CSαPIM耦合法和ESFEM/CSαPIM耦合法對上述耦合模型進行模態分析。首先把板結構和聲場分別離散成三角形和四面體網格，網格尺寸為0.05 m(結構域共148個節點，聲場域共1 003個節點)，并將不同方法得到的前20階耦合頻率列于表1中，與參考解進行比較。由于該問題沒有解析解，這里采用極其細密的等參元模型(單元尺寸為0.01 m，結構域共3 111個節點，聲場域共127 551個節點)提供參考解。為了更好地比較計算方法的優劣性，表2列出了參考解模型計算得到的結構與聲場的前10階固有頻率。

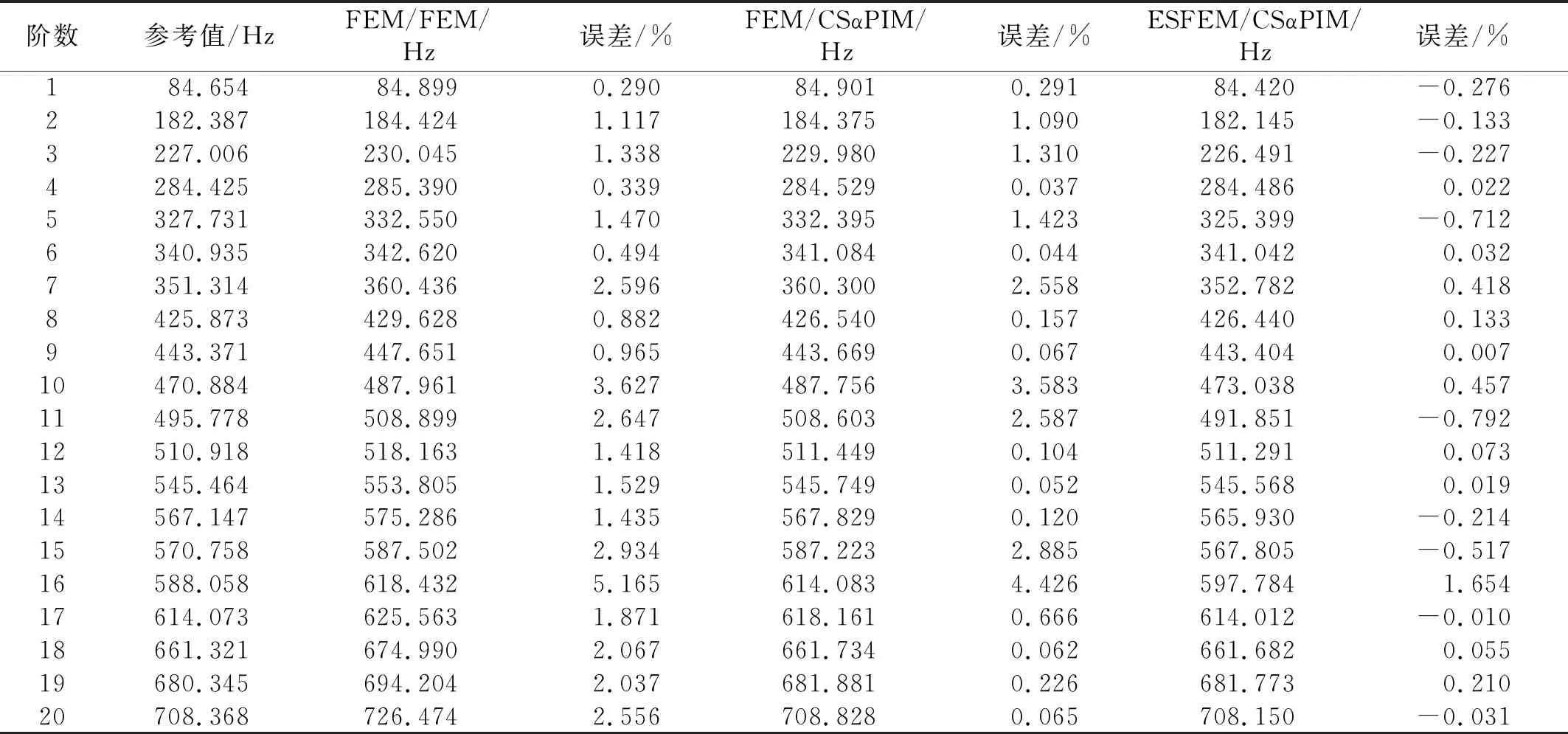
表1 柔性板與聲腔耦合系統的前20階耦合頻率Tab.1 The former 20th eigenfrequencies of coupled systems with flexible plate and cavity

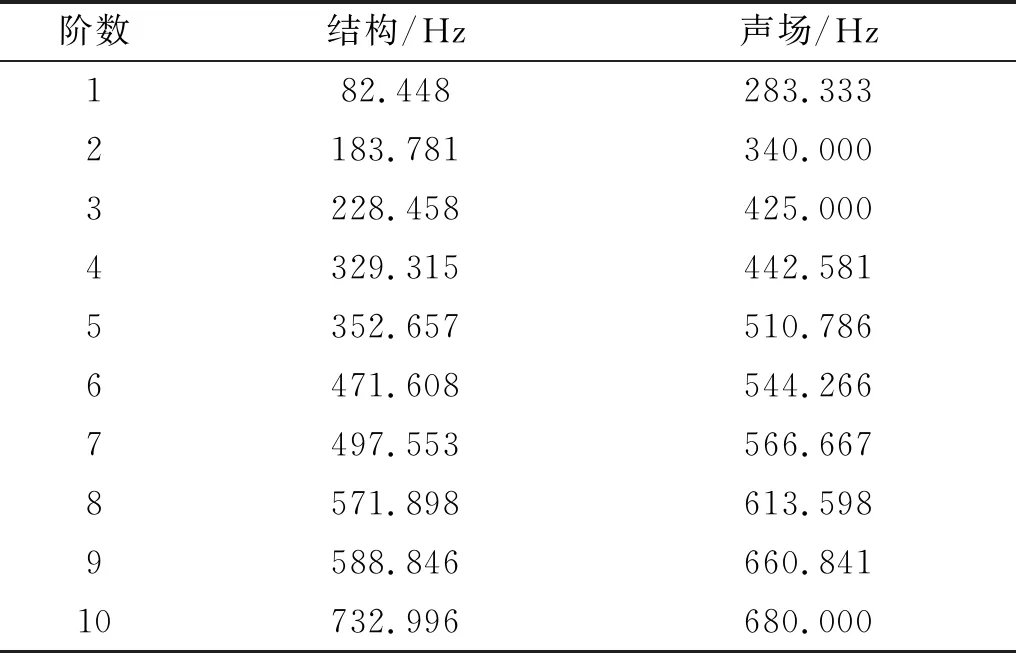
表2 結構與聲場各自的前10階固有頻率Tab.2 The former 10th eigenfrequencies of structure and acoustic domain

從表1和表2的結果，我們可以發現：

(1)FEM/FEM耦合法得到的特征頻率均比參考值高，這是由有限元過硬的剛度造成的；

(2)FEM/CSαPIM耦合法計算的特征頻率相比FEM/FEM耦合法明顯更接近于參考值，說明CSαPIM可以很好地模擬聲場的剛度，進而提高計算精度。其中，有幾階固有頻率的計算值相比FEM/FEM沒有較大改善(包括第7階、第10階和第11階、第15階和第16階)，是因為這幾階頻率與結構固有頻率較接近，聲場固有頻率的參與比例較低，而此耦合法只改變了聲場的計算方法。同理，精度有明顯提高的耦合頻率計算值與聲場固有頻率較接近(例如第9階、第13階和第18階)。

(3)ESFEM/CSαPIM耦合法對特征值的計算精度在3種方法中最高，在特征頻率階次較高時優勢更為突出。除了第16階頻率，其他的特征值誤差均小于1%。這是因為它不僅能更好地模擬聲場剛度，還能得到更合適的結構剛度。

5.2 結構聲場響應分析

頻率響應分析時振動噪聲模擬中必不可少的一環。為了進一步評價CSαPIM與ESFEM結合進行聲固耦合分析的效果，本節分別用FEM/FEM和ESFEM/CSαPIM耦合法對耦合系統的頻率響應進行數值模擬，在圖7所示板的中心點施加幅值為1 N的簡諧激勵，方向沿z軸。

圖8和圖9分別繪制了結構節點1(板的中心點，坐標為[300，200，400])的位移響應曲線和聲場節點2(某棱邊的中點，坐標為[0，0，200])的聲壓響應曲線，頻率范圍為0～800 Hz，間隔為2 Hz。為了驗證ESFEM/CSαPIM耦合法的魯棒性，圖中同時給出了其在規則網格和畸變網格下的計算結果，網格劃分細節如圖10所示。參考解同樣用5.1所描述的等參元模型獲得。結果表明，在0～200 Hz內，兩種方法都能得到很好的響應結果；隨著激勵頻率的增大，ESFEM/CSαPIM耦合法計算所得的結果相比FEM/FEM耦合法與參考解更加吻合，無論是結構和聲場的響應峰值，還是峰值所對應的頻率，都與參考解非常接近。這說明新方法由于準確地模擬了系統剛度，可以大大提高聲固耦合響應的計算精度。也就是說，在采用相同網格尺寸的基礎上，ESFEM/CSαPIM耦合法的可計算頻率范圍比FEM/FEM耦合法更廣，計算精度可以明顯提高。另外，雖然ESFEM/CSαPIM耦合法在畸變網格下的計算結果比規則網格的結果差，但仍優于FEM/FEM耦合法，說明了ESFEM/CSαPIM耦合法的魯棒性好。

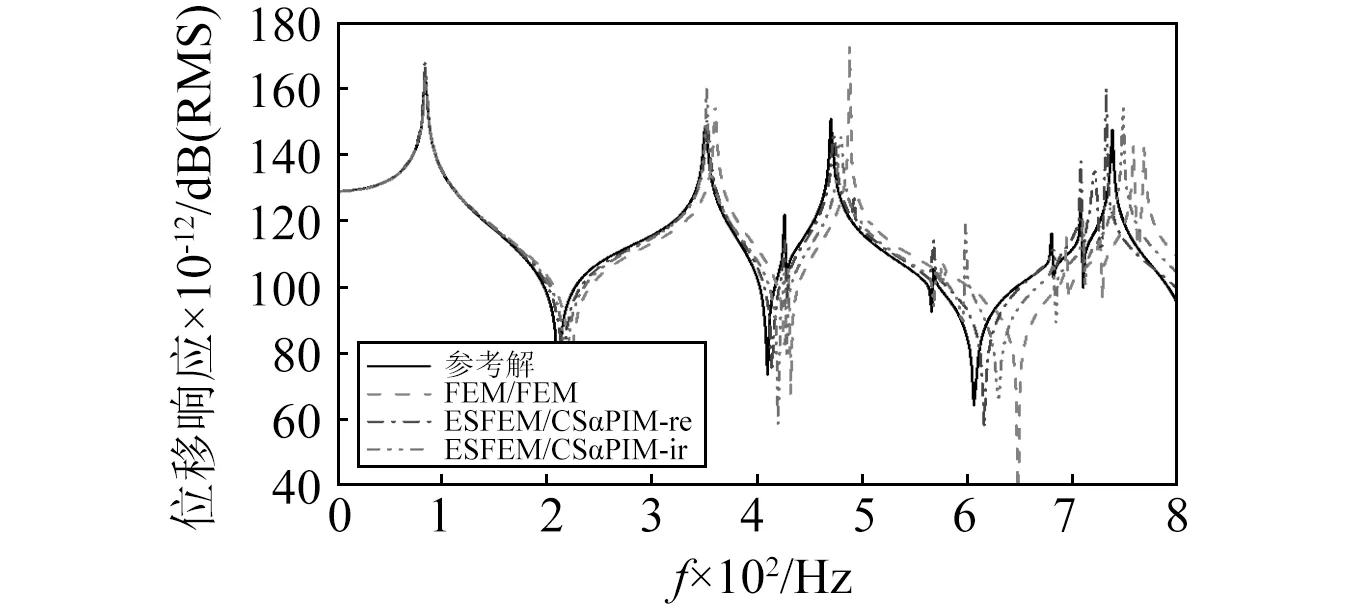
圖8 結構節點1的頻率響應曲線Fig.8 Frequency response curves of structure node 1

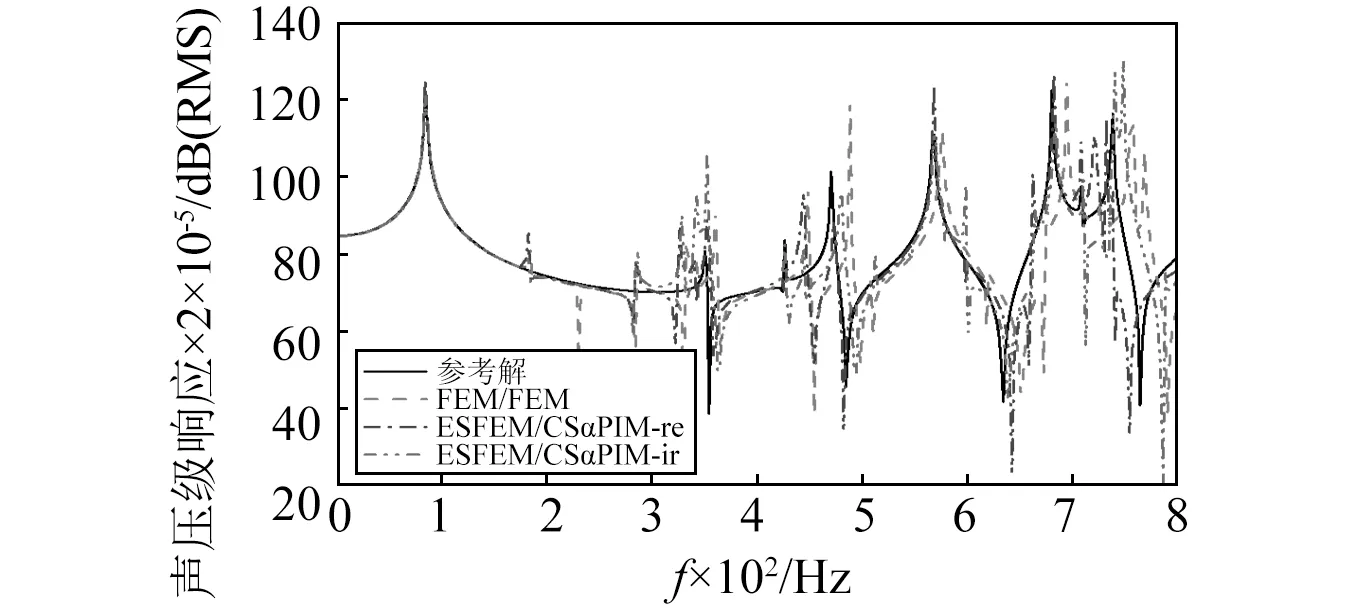
圖9 聲場節點2的頻率響應曲線Fig.9 Frequency response curves of acoustic node 2

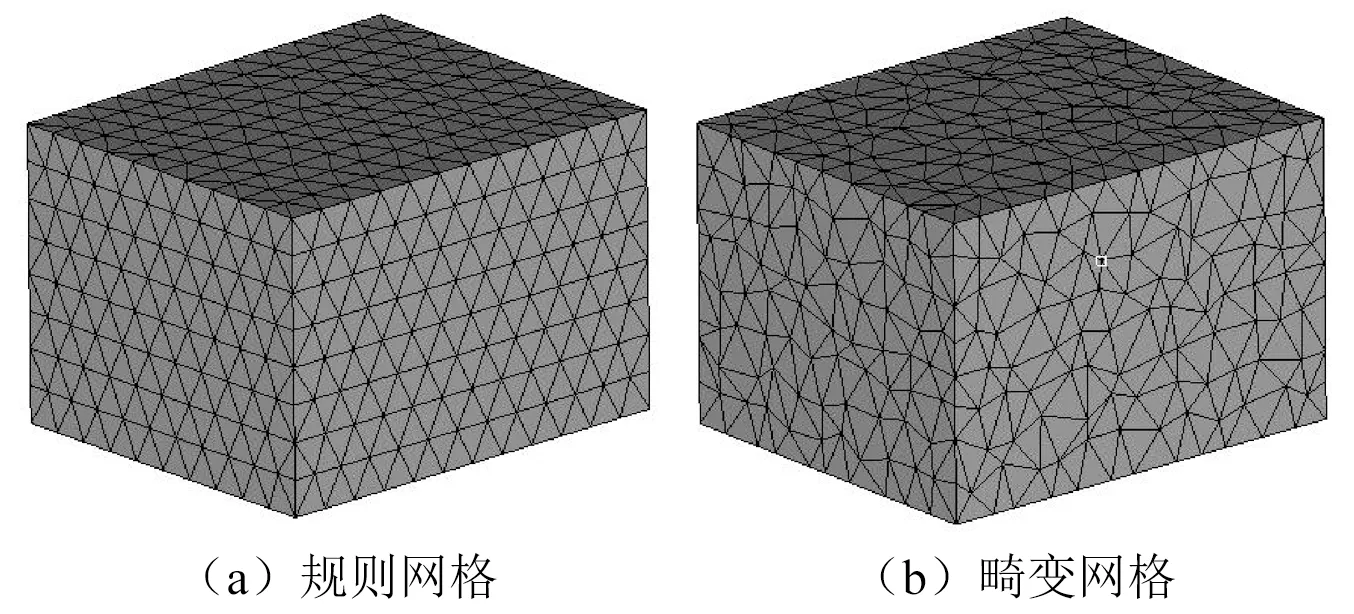
圖10 網格劃分細節Fig.10 Details of the meshes

6 結 論

本文將CSαPIM應用于三維聲學計算中，通過基本算例確定合適的α值，并與基于ESFEM的二維Mindlin板單元結合，對聲固耦合系統進行特征頻率預測和頻率響應分析，得到如下的結論：

(1)當α取經驗值0.6時，CSαPIM能獲得與連續系統非常接近的剛度，明顯提高聲學計算的精度。

(2)與FEM/FEM耦合法相比，ESFEM/CSαPIM耦合法在相同的網格尺寸下，計算得到的模態特征值更接近參考解，而且頻率響應的可計算范圍得到有效擴展，可以通過較低的網格要求達到相同的計算精度。

(3)ESFEM/CSαPIM耦合法分別采用三角形單元和四面體單元離散結構域和聲場域，可以適應各種復雜幾何模型，減少前處理時間，魯棒性好，具有良好的工程應用前景。