穩定器作用下坦克行進間炮口振動特性研究
陳 宇,楊國來
(南京理工大學 機械工程學院,南京 210094)
坦克具有良好的越野性能,坦克行進時,車體(包括火炮)隨著地面的起伏而振動,嚴重影響炮手對目標的捕獲和瞄準,使得行進間射擊的命中率不高。而坦克穩定器是坦克行駛中自動將炮膛軸線保持在賦予的空間角位置并能瞄準的一種控制系統,是現代坦克火控系統的重要組成部分,能有效提高坦克行進間射擊的命中率[1]。目前,對于坦克穩定器的研究較多,但主要著重于穩定器控制方法的研究,Gao等[2-4]分別基于自抗擾控制、模糊控制、魯棒控制方法建立了坦克穩定器控制系統,研究了其對坦克行進間穩定精度的影響,研究中一般會對坦克動力學模型進行簡化,將其看作一個線性傳遞函數。事實上目前火炮穩定器設計時一般將火炮作為線性系統,認為炮口振動情況與搖架完全相同,因此為控制系統提供系統輸入的角度陀螺儀及角速度陀螺儀都安裝在搖架上,其穩定目標是搖架。但由于身管柔性及其與襯瓦間存在間隙等非線性因素影響,即使在坦克穩定器正常工作情況下,坦克行進間炮口振動與預期的穩定精度仍存在較大差異,當坦克行駛速度及彈丸出炮口速度不高時,該差異較小。但隨著現代坦克對于高機動、高初速和高精度要求的不斷提高,這一差異逐漸凸顯,不容忽視。
但坦克構造復雜,造價高昂,通過實物樣機研究的時間成本和經濟成本都較大。目前,虛擬樣機技術被廣泛運用于武器設計研究的各個階段,大大降低了坦克的設計和試驗成本。大量學者對坦克行進間射擊的過程進行了研究,但研究中一般都忽略了坦克穩定器的影響。劉飛飛等[5-6]通過建立身管柔性的坦克行進間發射動力學模型,考慮彈丸動不平衡及質量偏心、彈炮相互作用及間隙,建立行進間彈丸膛內運動方程,獲得了彈丸膛內運動規律,分析說明了考慮身管柔性影響有利于獲得準確的彈丸起始擾動;徐達等[7]通過建立了考慮身管柔性的坦克全車動力學模型,分析說明了相對于剛性身管,柔性身管模型能有效提高坦克炮射擊仿真精度;史力晨等[8]通過狀態方程法建立了坦克、火炮系統的振動模型,將系統的動力學響應看作了多剛體系統對地面不平度激勵的響應問題,穩定器作用通過剛性系數體現,計算分析了坦克行進間火炮運動規律;金濤等[9]通過建立坦克多剛體模型,采用PID(Proportion Integration Differentiation)控制對坦克火炮進行控制,說明了在坦克高速行駛時,PID控制依然能較好控制火炮振動;Purdy等[10]采用PI控制方法,通過建立某主戰坦克高低機電動控制系統的非線性模型,計算發現非線性摩擦會降低控制系統的性能。
目前,關于機電耦合問題的研究已經取得了眾多的成果[11]。但目前針對坦克穩定器的機電耦合問題研究還鮮見報道。本文擬采用PID控制方法,在MATLAB/Simulink環境下對坦克垂向穩定器進行復現。通過 RecurDyn/Control模塊將建立的動力學模型與坦克垂向穩定器系統相結合,得到完整的機電耦合動力學模型。通過數值計算,分析了非線性因素(身管柔性和身管襯瓦間隙)對穩定器作用下坦克行進間炮口振動特性的影響。此外,文中還重點研究并證實了將炮口高低角位移作為垂向穩定器的控制目標能有效抑制坦克行進間的垂向炮口振動。
1 坦克行進間機電聯合建模原理
坦克行進間機電聯合建模的主要內容包括坦克系統三維建模、非線性動力學建模、穩定器控制系統建模及接口技術。其中動力學采用RecurDyn建模,控制系統采用Matlab軟件的Simulink模塊實現,聯合仿真的平臺為RecurDyn/Control模塊。圖1為機電聯合建模的框架圖。

圖1 坦克行進間機電聯合建模框架圖Fig.1 Electromechanical coupling modeling of tank on the move
建模難點在于實現動力學模型與控制系統的實時數據交換。本文利用RecurDyn完成坦克系統的動力學建模,并生成Simulink能夠識別的被控制模塊,在Simulink中建立穩定器控制模型,利用RecurDyn/Control工具箱實現機電一體化聯合計算時的實時雙向數據傳輸,圖2所示為其工作原理。機械系統通過RecurDyn解算器進行計算,控制系統通過控制軟件解算器進行計算,兩者之間通過狀態方程聯系,在每個固定的取樣時間步內都會進行一次數據交換,當取樣時間足夠小時,可以近似認為在單個取樣時間內,系統不發生變化,即近似認為數據交換是實時的。
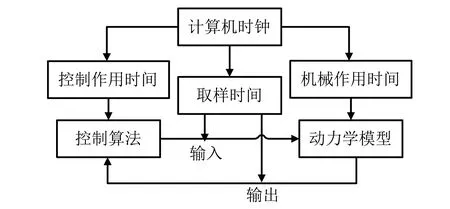
圖2 RecurDyn/Control工作原理示意圖Fig.2 Operating principle of RecurDyn/Control
2 坦克系統動力學模型
本文建模時暫只考慮坦克垂向穩定器作用,故在此主要分析坦克系統火炮高低向運動,圖3為運動簡圖,坦克車體的運動可以用作用于車體質心位置處的垂向運動yp和轉動θp表示。當車體發生小范圍轉動時,耳軸處的運動可以近似用一個垂向運動yt和轉動θp來表示,那么耳軸處的垂向位移和垂向加速度可表示為
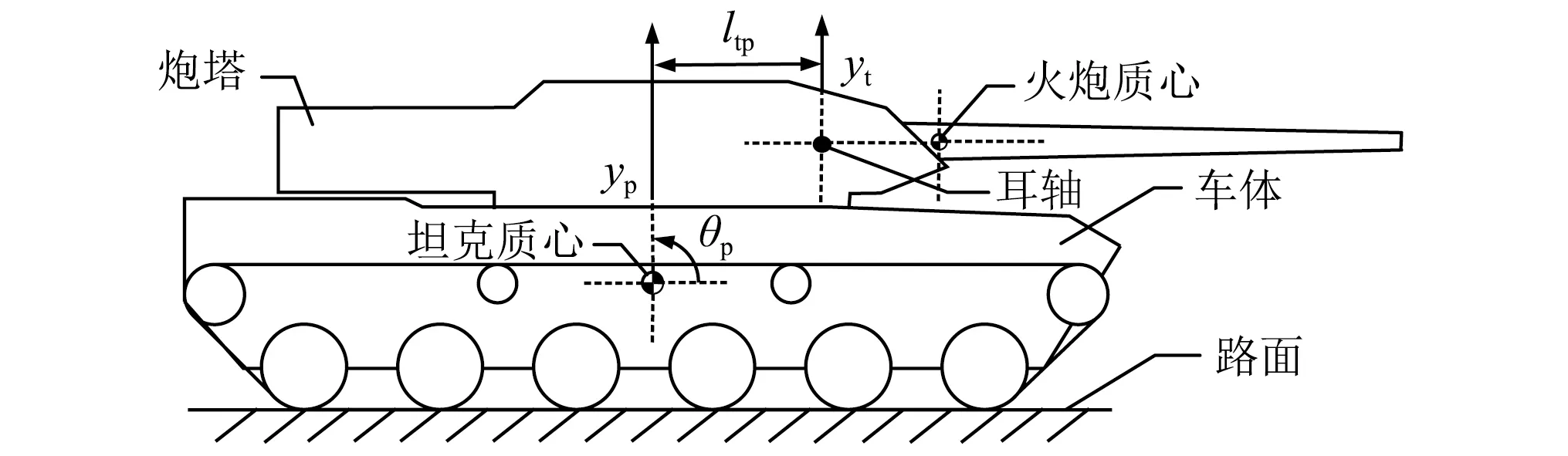
圖3 坦克系統火炮高低向運動簡圖Fig.3 Kinematic sketch of tank in elevation
yt=yp+θpltp
(1)
(2)
式中:ltp為車體質心位置距離耳軸處的水平距離。
火炮部分受力分析如圖4所示。分析時,將動力油缸簡化為作用于驅動位置點與炮塔之間的無質量彈簧系統,等效剛度為kd,則驅動位置點軸向力fd可表示為
fd=kd[yd-ltd(θ1-θp)]
(3)
式中:yd為活塞和活塞桿相對油缸壁的移動距離;θ1為火炮繞質心在高低方向的轉角;θp為坦克在高低向繞坦克質心的轉角。
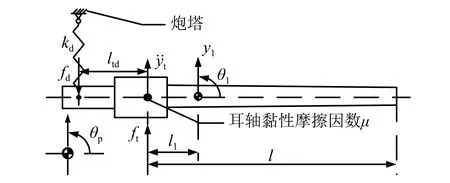
圖4 火炮部分受力分析圖Fig.4 Stress diagram for part of gun
此外火炮質量為m,其繞質心的轉動慣量為I,炮口距耳軸中心距離為l,火炮質心位置距耳軸中心距離為l1,動力油缸在搖架上驅動位置距耳軸中心距離為ltd。火炮在耳軸點所受的垂向作用力為ft;耳軸處等效黏性阻尼為μ。則火炮部分受力分析
(4)
式中:yt為火炮質心處的垂向位移;且其與耳軸存在以下幾何約束關系
yt=y1-θ1l1
(5)
(6)
某坦克垂向火炮穩定器[12]是一個電液式自動調整系統,主要由角度陀螺儀、角速度傳感器、電子放大器、液壓放大器、動力油缸、角速度陀螺儀、火炮等組成。火炮垂向穩定器的結構圖,如圖5所示。
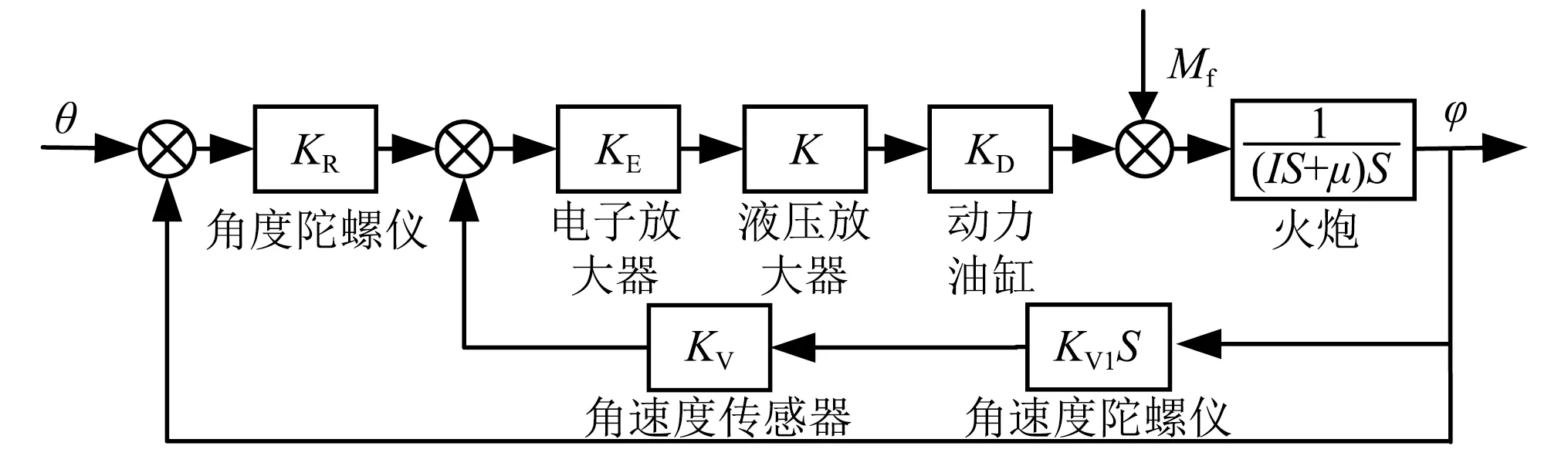
圖5 某坦克垂向火炮穩定器結構圖Fig.5 Structure diagram of the vertical stabilizer
圖5中:KR,KE,K,KD分別為角度陀螺儀、電子放大器、液壓放大器、動力油缸的放大系數;I為火炮轉動慣量;μ為火炮的黏性摩擦因數;Mf為干擾力矩;KV,KV1分別為角速度傳感器和角速度陀螺儀的放大系數;θ為輸入;φ為火炮高低角。則垂向火炮穩定器的數學模型可表示為[13]
(7)
式中:G1=KDKKEKR為穩定器對誤差角的放大倍數;G2=KDKKEKV為穩定器對角速度陀螺儀內環轉角的剛性。
所建立的坦克垂向穩定器系統以搖架高低角位移為控制目標變量,將搖架的實際高低角位移與目標高低角位移(即瞄準角)進行比較產生誤差;控制系統通過動力油缸輸出控制力,機械系統模型根據輸入控制力大小,對搖架高低角位移進行調整,并將角位移信息反饋給控制系統,形成閉環控制。系統有一條前向通路,兩個閉合回路,除了角位移反饋回路,還有一個速度反饋回路。在兩個回路的協調控制作用下,可維持穩定工況條件下火炮的穩定。
本文選擇PID控制來設計坦克垂向穩定器。PID控制是一種線性控制方法,算法表示為[14]
(8)
式中:Kp為比例系數;Ti為積分時間常數;Td為微分時間常數。PID控制的難點在于控制參數的整定,可以根據控制器的參數與系統動態性能和穩態性能之間的定性關系,用試驗的方法來調節控制器的參數。
3 坦克行進間機電耦合建模
3.1 坦克非線性動力學建模
如圖6所示,該坦克主要包含底盤和火力部分,并以上下座圈相連接。底盤由車體、負重輪、拖帶輪、誘導輪、驅動輪和履帶板等組成,其他部件質量和慣量通過計算等效至車體上。履帶板與地面間為剛性接觸。
圖6 坦克行進間多體系統虛擬樣機模型Fig.6 The multibody system virtual prototype model of tank on the move
火力部分主要包括后坐部分、搖架部分、炮塔部分。身管為模態柔性體,與炮尾通過后端面界面節點固定連接。分別建立身管與前后襯瓦的剛柔接觸碰撞[15],并采用非線性彈簧阻尼模型計算其法向接觸力f的表達式為
(9)
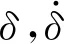
c(δ)=step(δ,0,0,dmax,cmax)
(10)
式中:cmax為法向最大阻尼系數;dmax為最大允許穿透深度。利用c語言編寫用戶子程序,并利用二次開發功能在軟件中插入用戶子程序。其它構件簡化為剛體,并通過理想約束連接。駐退機和復進機載荷分別通過函數擬合,并直接加載在適當位置。
3.2 三維路面模型
路面不平度是指道路表面相對已知理想基準平面的偏離程度。通過對振動傳遞路徑的分析可以發現,在坦克行駛過程中,路面對左右履帶的激勵,經過懸掛衰減后傳遞至車體,經由座圈傳遞至炮塔,再經過耳軸傳遞給火炮主體,造成后坐部分的振動,從而影響彈丸運動,造成對射擊精度的不利影響,因此建模的要點是準確地重構路面不平度。本文選擇采用諧波疊加法基于Mathematica數學工具編寫路面譜程序。
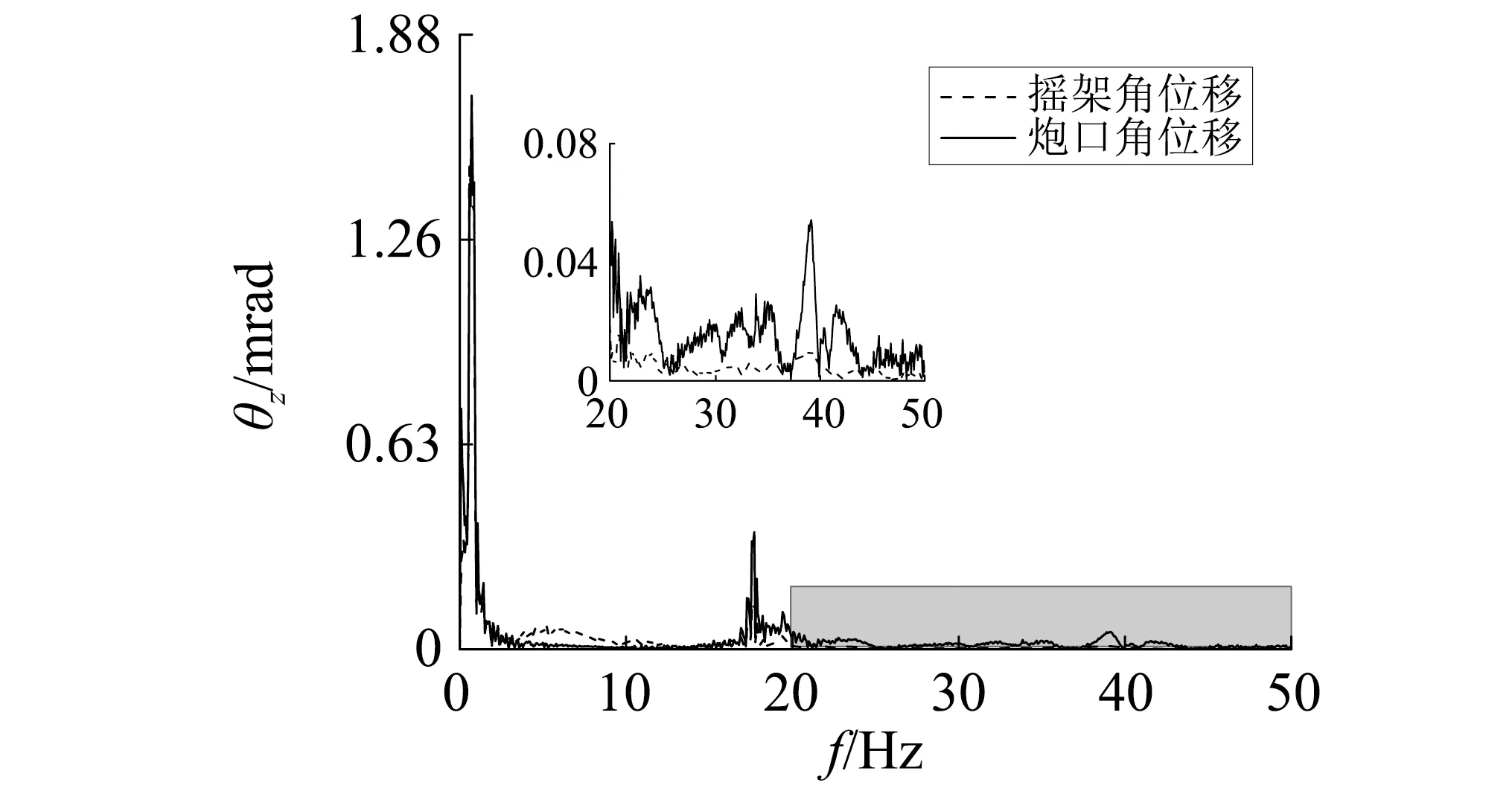
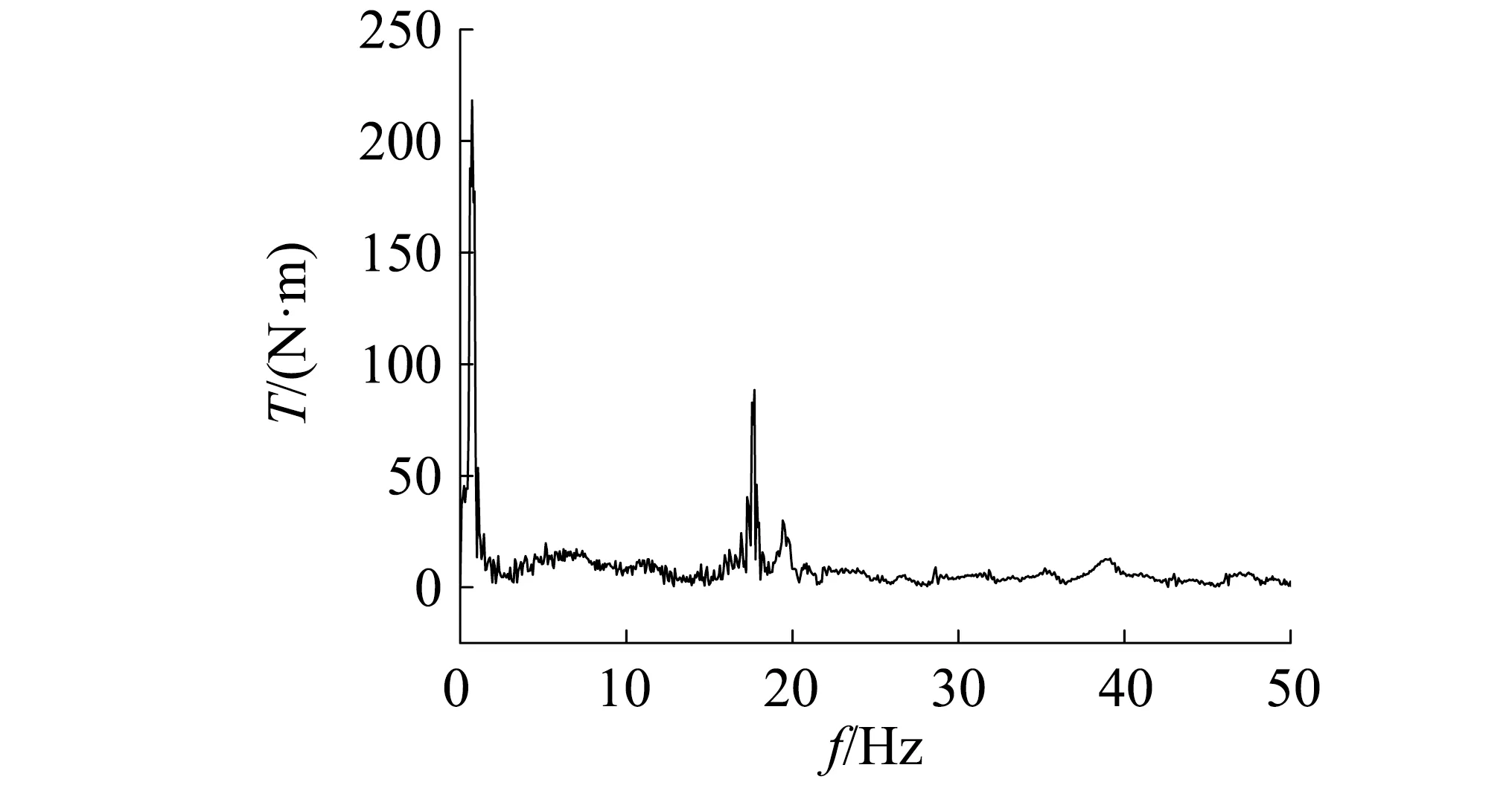
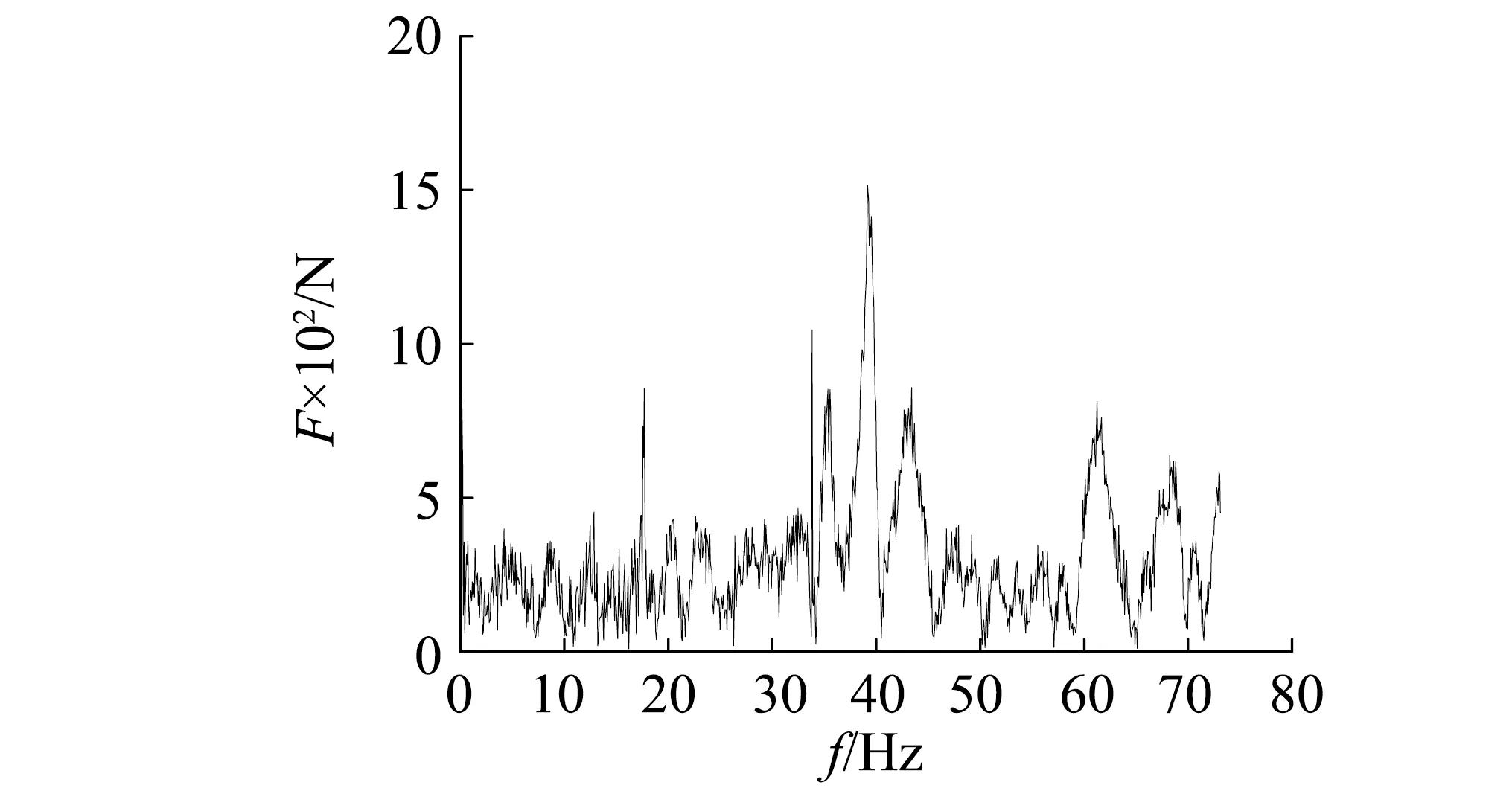
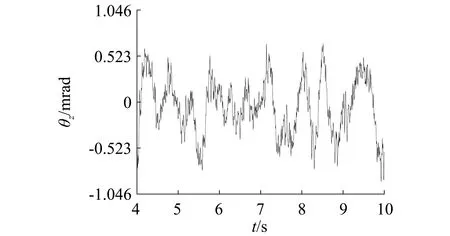
將路面空間頻率f(f1 (11) 式中:x為路面在X方向上的位移;α為[0,1]上均勻分布的隨機數;Ai為中心頻率fi對應的諧波的振動幅值 (12) 此外實際行駛過程中,坦克左右履帶受到的來自地面的激勵并不相同,兩側車輪所受路面激勵的相干性可表示為 (13) 式中:dv為輪距;ρ為經驗值;n1,n2分別為路面空間頻率的上下限。 由于路面不平度函數中的隨機相位角α是引起左右履帶激勵差異的主要因素,因此三維路面不平度隨機過程可以表示為 (14) (15) 式中:αx為x方向路面不平度激勵的隨機相位;αn為新生成的[0,1]的隨機數。 根據上式編寫三維路面譜程序,重構了長100 m、寬5 m的D級三維路面不平度模型,并通過節點縫合法生成軟件可讀取的路面文件。 垂向火炮穩定器在坦克行進過程中是通過動力油缸提供火炮的穩定力矩,建模時,忽略動力油缸及相關構件,并通過計算將重量及慣量合并到炮塔及炮尾部分。在耳軸處施加一個反向力矩模擬動力油缸的控制作用,創建輸入狀態變量,并與反向力矩相關聯。設定狀態變量為輸入變量,設定搖架高低角位移以及PID控制的三個控制參數為輸出變量,在RecurDyn/Control模塊下導出聯合仿真接口文件,在建立好的Simulink控制模型中取代火炮傳遞函數,構建坦克行進間機械-控制聯合仿真系統模型。其中,RecurDyn為主程序,控制系數可直接在主程序中修改。聯合仿真系統模型如圖7所示。 圖7 聯合仿真系統模型Fig.7 System model of Co-simulation 火炮穩定精度為坦克行駛在起伏路面上時,火炮擺動振幅的算術平均值,表達式為 (16) 式中:N為采樣的總點數;θi為采樣得到的火炮高低向角位移。數值計算時,通過給坦克主動輪施加驅動力模擬坦克行駛過程。本文選擇對坦克以20 km/h速度行駛在D級路面上時的炮口振動進行計算分析。由于前4 s坦克處于速度不穩定狀態且建模時僅考慮了垂向穩定器,因此在分析時僅分析4 s后炮口高低向振動規律。 目前,在設計坦克垂向穩定器時,一般不考慮非線性因素影響,即認為炮口高低角位移與搖架高低角位移相同,為了證實本文所建立坦克高速行進間聯合仿真模型中控制方法的可行性,分別計算了考慮和忽略穩定器作用時坦克行進間搖架處振動情況。 由圖8可知,不考慮穩定器作用時,搖架處的高低振動幅值最大為11.69 mrad,顯然,在此條件下難以完成準確射擊并命中目標的動作。而穩定器控制作用后,通過控制系數調整,搖架高低角位移得到了有效控制,其最大幅值顯著減小至3.01 mrad,最終能夠保證穩定精度約0.98 mrad,而根據朱競夫等的研究可知目前火炮垂向的穩定精度約為0.52~1.05 mrad,這說明計算結果能滿足實際穩定精度要求,說明了控制方法具有可行性,也間接驗證了所建機電耦合模型的準確性。 圖8 坦克行進間搖架高低角位移Fig.8 Vertical cradle angular displacement of tank on the move 坦克實際行駛過程中,后坐部分構件柔性及構件間碰撞等非線性因素是現實存在的,為了分析這些非線性因素對于炮口高低角位移的影響,本文選擇在機電耦合模型中考慮身管柔性及身管襯瓦間隙兩個最顯著的非線性因素,計算了此條件下坦克行進間搖架和炮口振動響應。同過對控制參數進行調整,得到搖架和炮口振動的振幅比較,如圖9及表1所示。 圖9 搖架和炮口高低角位移對比Fig.9 Vertical angle displacement comparison between muzzle and cradle 表1 搖架和炮口高低角位移比較Tab.1 Vertical angle displacement comparison between muzzle and cradle 由圖9可知,坦克行進間搖架處和炮口高低角位移差別很大,由于身管自重的原因,再考慮身管柔性因素后,身管會發生向下的彎曲,在圖9中體現為炮口高低角位移較搖架處整體偏小。但兩處高低角位移的曲線波形幾乎一致,這說明當坦克在較平坦路面以較低速度行駛時,路面激勵還是影響炮口及搖架處高低角位移的主要因素。由表1可知,炮口處穩定精度為3.36 mrad較搖架處的0.98 mrad增大了241.49%;炮口高低角位移的標準差為1.26 mrad較搖架處的1.13 mrad增大了11.11%。這說明考慮身管襯瓦間隙和身管柔性這兩種非線性因素后,炮口振動高低角位移顯著大于搖架處,同時炮口高低向振動振幅也大于搖架處。 通過以上分析可知傳統穩定器設計過程中的假設與實際并不相符,因此,按照傳統方法設計的穩定器,不可避免的存在一定誤差,身管襯瓦間隙和身管柔性這兩種非線性因素會嚴重降低了坦克垂向穩定器的穩定效果,顯然,這不利于提高坦克行進間射擊精度,需要針對這一問題進行更深入的研究。 圖10給出了坦克行進間搖架和炮口高低角位移頻域圖,圖11給出了坦克穩定器穩定力矩頻域圖,由圖可以看出,三條曲線的主峰值對應的頻率都為0.87 Hz,其與坦克車體自身頻率相近,因是由坦克車體振動造成的,其第二峰值對應的頻率都為17.62 Hz,與身管一階模態頻率相近,應是由坦克炮身管彎曲造成的。此外由圖10中局部放大圖可以看出炮口處高低角位移頻域圖的第三峰值約為39.20 Hz,這與由圖12給出的前襯瓦與身管接觸力頻域圖主峰值對應的頻率相近,應是由坦克炮身管襯瓦接觸造成的。因此,在坦克行進過程中,車體振動對于炮口高低角位移的影響依次大于身管彎曲和身管襯瓦接觸影響。同時,坦克行進間炮口高低角位移頻域圖中的高頻信號明顯強于搖架處高低角位移頻域圖,這同樣是由身管襯瓦接觸及身管柔性這兩種非線性因素造成的。 圖10 搖架和炮口高低角位移頻域圖Fig.10 Frequency range chart of the vertical angle displacement of muzzle and cradle 圖11 穩定力矩頻域圖Fig.11 Frequency range chart of stabilizing moment 圖12 前襯瓦與身管接觸力頻域圖Fig.12 Frequency range chart of contact force between the front bushing and the barrel 目前,在設計坦克垂向穩定器時,一般不考慮身管彎曲和身管襯瓦間隙(即身管為剛性體,身管與搖架簡化為滑移鉸連接),此時炮口高低角位移與搖架高低角位移相同,選擇搖架處的高低角位移作為控制系統輸入,即控制目標為搖架的高低角位移,由上文分析可以發現,由于非線性因素的影響,炮口振動位移幅值顯著大于搖架位移幅值,且炮口處于高頻振動狀態,顯然這不利于控制炮口振動,提高坦克行進間射精精度。針對這一問題,本文嘗試將坦克垂向穩定器的控制目標改為炮口處的高低角位移。 在建立的機電耦合動力學模型中,通過位移函數導出炮口處垂向角位移,再利用M文件將其導入到建立的垂向穩定器控制模型作為模型的系統輸入。而在實際坦克中可通過在炮口處安裝電渦流位移傳感器測量炮口垂向位移,并通過計算后傳遞至穩定器作為輸入。 對坦克以20 km/h速度行駛在D級路面上時的炮口振動進行計算分析,得到了穩定器控制結構改進后的炮口垂向角位移,如圖13所示。由圖13可知,炮口處的高低擺動振幅的極值由原穩定器控制結構情況下的14.11 mrad減小為0.91 mrad,減小了幅度達93.55%;穩定精度由3.36 mrad減小為0.26 mrad,減小幅度達92.21%,說明控制結構改進對于提高穩定精度效果明顯。綜合以上可以得出,穩定器控制結構改進對于減小炮口振動幅值有很好的效果,這有利于提高坦克行進間的射擊精度。 圖13 坦克行進間炮口高低角位移Fig.13 Vertical muzzle angular displacement of tank on the move 本文基于RecurDyn/Control模塊將建立的考慮多個非線性因素的坦克行進間剛柔耦合動力學模型與坦克垂向穩定器系統相結合,得到完整的機電耦合動力學模型。通過數值計算對坦克在穩定器作用下的行進間炮口振動特性進行分析,結果表明在坦克行進過程中,車體振動是影響炮口高低角位移最主要因素。坦克垂向穩定器能有效減小坦克行進間搖架和炮口處的垂向振動。但身管柔性及身管襯瓦間隙造成炮口處高低角位移仍遠大于搖架處高低角位移,顯然這不利于保證行進間射擊精度。為了有效減小炮口垂向振動,提出了改進垂向穩定器控制目標為炮口處高低角位移的方法,通過數值計算證明方法能有效減小坦克行進間炮口高低角位移,有利于提高坦克行進間射擊精度。但本文研究中未考慮動力機構的建模,而是采取直接控制的手段,所建模型與實際情況仍存在一定差異,這將在今后工作中逐步完善。3.3 聯合建模

4 炮口振動數值計算與分析
4.1 控制方法可行性分析

4.2 非線性因素影響
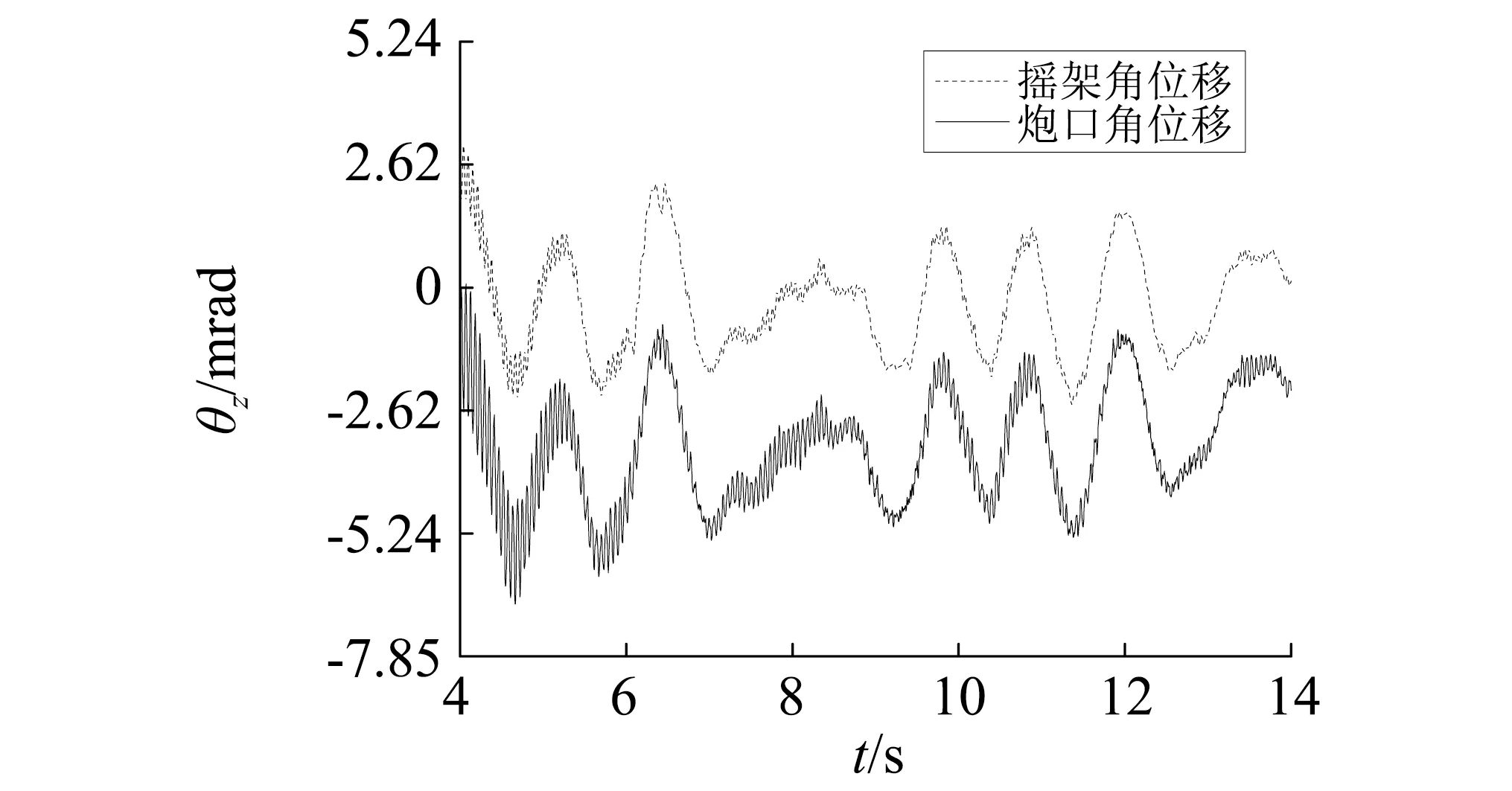
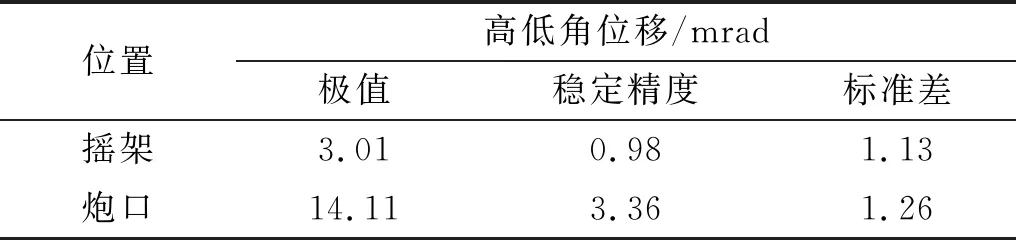
4.3 穩定器控制目標改進
5 結 論

