基于擴展有限元模型的動態應力強度因子計算

汪必升 李毅波,2 廖雅詩 李 劍

1.中南大學機電工程學院，長沙，4100832.中南大學高性能復雜制造國家重點實驗室，長沙，4100833.中南大學輕合金研究院，長沙，410083

0 引言

裂紋擴展中的應力強度因子不僅體現了裂紋尖端的應力奇異性，還反映了應力與幾何缺陷之間的關系，是表征裂紋尖端應力場與位移場的關鍵參數[1]。研究動態裂紋擴展中應力強度因子的計算方法，分析影響計算精度的關鍵參數并確定其參考范圍，對提高應力強度因子計算精度與效率、實現關鍵結構裂紋擴展剩余壽命預測具有重要的科學意義與應用價值。

計算應力強度因子的常用方法有解析法、實驗法和數值法。解析法和實驗法受條件所限，一般用在簡單幾何結構和靜載條件；有限元法[2]、無網格法[3]及邊界元法[4]等數值法因不受幾何結構或載荷情況的影響，可模擬出一般帶裂紋件，受到了國內外的關注。

常規的有限元方法求解非連續位移場時依賴于單元邊界，進行裂紋擴展模擬時往往需要預定裂紋擴展路徑或進行網格重劃分。BELYTSCHKO等[5]在有限元法基礎上提出的擴展有限元法(extended finite element method，XFEM)，不僅保留了傳統有限元法的優點，還很好地解決了因材料和幾何結構而帶來的不連續問題，故XFEM得到了迅速發展，已成為裂紋擴展分析最主要的方法之一。由于存在裂紋尖端坐標、裂紋與單元切割點難以精確確定以及裂紋在單元內會發生轉折等問題，采用有效方法精確計算XFEM模型中的應力強度因子一直是國內外研究的熱點。NEHAR等[6]通過XFEM來模擬脆性和雙材料界面的裂紋擴展，利用位移跳躍法計算應力強度因子，該計算值與理論值能很好地吻合 。周博等[7]采用基于XFEM的應力外推法對平板裂紋的應力強度因子進行計算，他們發現，純Ⅰ型裂紋的精度較高且易于實現。GUO等[8]通過相互作用積分法計算非均質材料受熱載荷下的應力強度因子，其結果與理論解有較好的一致性。ZHENG等[9]利用相互作用積分法與XFEM結合計算了帶孔裂紋平板準靜態下裂紋尖端的應力強度因子，并引入再分析技術，顯著地減少了計算過程中的迭代次數，但缺乏實驗驗證。艾書民等[10]利用Franc3D軟件求解裂紋擴展過程中的應力強度因子，通過疲勞壽命預測得到了驗證，但其基本原理還是基于有限元法，需對網格進行加密及重復網格劃分。

目前，國內外針對XFEM模型應力強度因子的計算大多集中在某型斷裂模式下的準靜態裂紋，有關在不同斷裂模式下動態裂紋擴展應力強度因子計算方面的報道較少，有學者雖探討了計算參數對應力強度因子計算結果的影響，但并未提出明確的計算參數范圍。為此，本文基于ABAQUS軟件的XFEM模塊分析，采用相互作用積分法，通過Fortran語言開發urdfil用戶子程序，分別對中心裂紋平板Ⅰ型斷裂模式、三點彎曲Ⅱ型斷裂模式下動態裂紋擴展過程的應力強度因子進行了計算，研究了網格密度和積分半徑對應力強度因子計算精度的影響規律，確定了較優的計算參數范圍；在對單邊帶孔疲勞擴展試樣的應力強度因子計算的基礎上，基于Paris公式預測了單邊帶孔試樣的剩余壽命，并進行了試驗驗證。

1 擴展有限元法的基本理論

擴展有限元法(XFEM)在傳統有限元法的框架上引入富集函數，以反映裂紋擴展帶來的非連續位移場，只有少數裂紋附近的單元被富集，大部分單元都保持傳統有限元單元位移模式。為此，需在有限元位移函數的表達式中增加反映局部特性的附加函數來間接模擬局部不連續性[11]，其描述裂紋含裂紋面的近似位移插值矢量函數可表示為

(1)

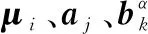
對于各項同性材料，裂紋尖端漸進位移場附加函數φα的向量表達形式如下[12]:

(2)

式中，s、θ分別為積分點在極坐標系下裂紋尖端到節點的距離和角度。

圖1所示為裂紋尖端采用單層加強時(即對裂紋尖端附近的一層節點進行加強)的加強節點分布，其中，“○”表示裂紋尖端節點，“□”表示貫穿節點，其余為常規節點(圖中未標出)。

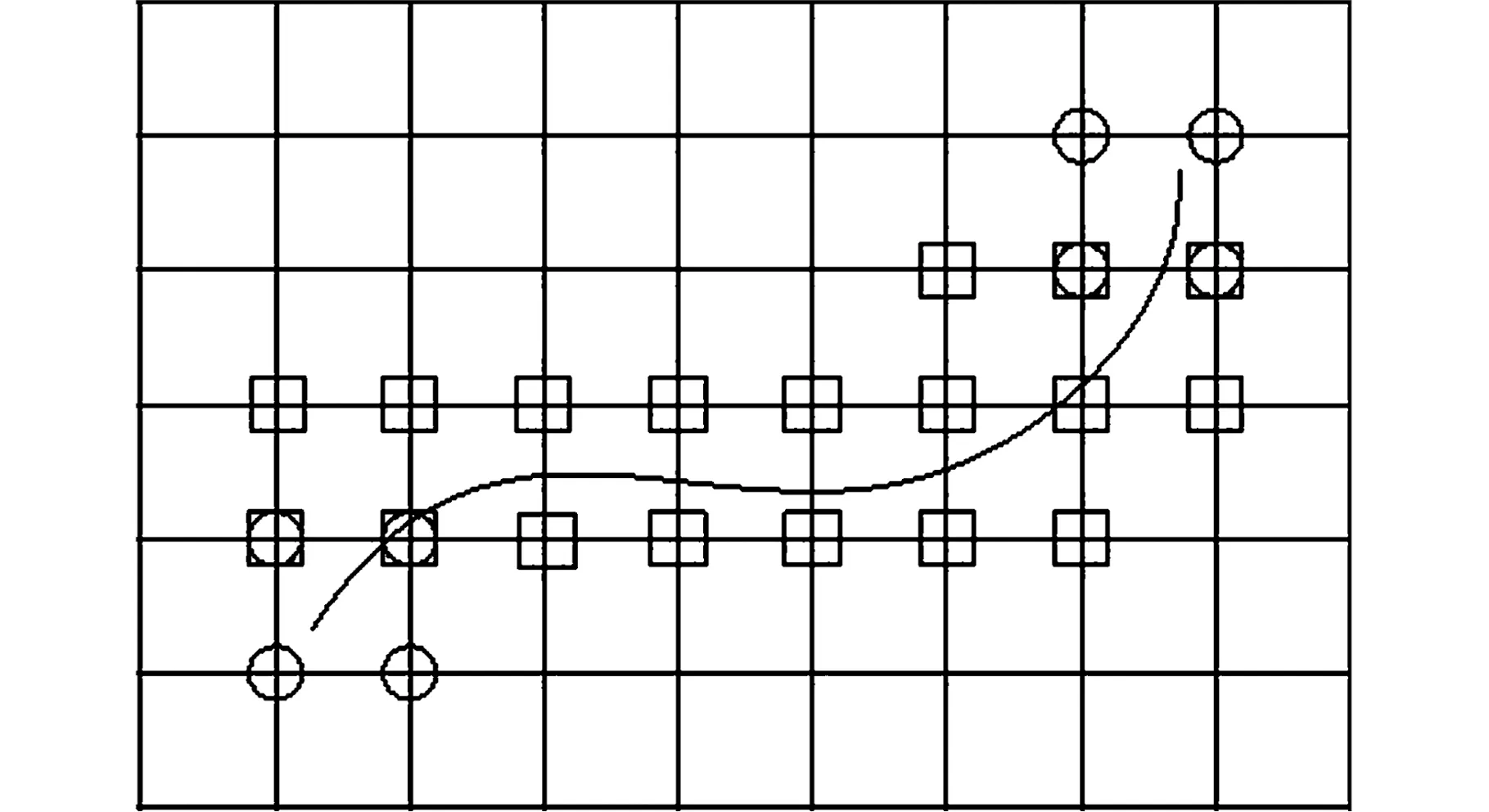
圖1 加強節點分布Fig.1 Enriched nodes distribution

對于含有兩種或兩種以上節點的混合單元，在式(1)位移模式下得到的節點處計算值不等于真實節點位移，需通過平移加強函數來糾正，相應的位移插值矢量函數可表示為

(3)

2 基于相互作用積分法的應力強度因子計算

2.1 相互作用積分法基本理論

相互作用積分法通過建立輔助應力場和輔助位移場來獲取和分離真實場中的Ⅰ型和Ⅱ型應力強度因子[13]。輔助應力場、輔助位移場是滿足平衡方程、物理方程和幾何方程關系的任一應力場和位移場；真實場則是物體待求裂紋尖端的應力場和位移場。

以二維裂紋擴展問題為例，如圖 2所示，裂紋用一條線段表示，在其尖端建立一個局部正交坐標系，其中，Г、C0分別為繞裂紋尖端的內圓和外圓周線；nj、mj分別為路徑Г和C0外法線的方向余弦；x1、x2分別表示方向1和方向2。

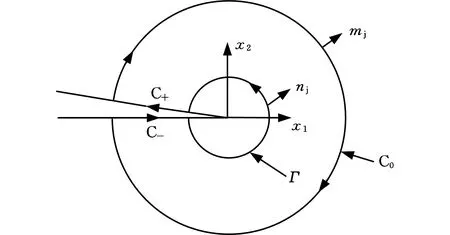
圖2 局部正交坐標系Fig.2 Local orthogonal coordinate system

定義J積分如下[14]：

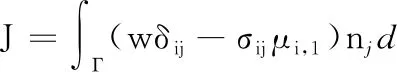
(4)

式中，w為應變能密度；δij為Kronecker函數；σij為應力分量；μi,1為方向i對方向1的位移偏導數。

為了分離混合模式下的應力強度因子KⅠ和KⅡ，利用疊加原理，選兩個獨立的平衡態，狀態1為真實場狀態，狀態2為輔助場狀態。將真實狀態和輔助狀態疊加后可得

(5)

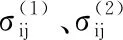
將式(5)轉換為

J(1,2)=J(1)+J(2)+I(1,2)

(6)

(7)

式中，I(1,2)為真實場和輔助場的交互積分；w(1,2)為真實場和輔助場的交互應變能密度。

各向同性材料的J積分與應力強度因子之間的關系可表示為

(8)

式中，E′為等效模量；E為材料的彈性模量，ν為材料的泊松比。

將兩個平衡態線性疊加可得第三個平衡態，并將第三個平衡態代入式(8)可得

(9)

取狀態2純Ⅰ型、純Ⅱ型的漸進應力場和位移場分別為f1、f2，由式(6)和式(9)分別可得

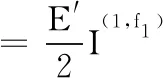
(10)

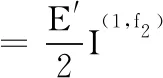
(11)

2.2 應力強度因子計算流程

采用ABAQUS軟件建立各試樣裂紋擴展的有限元模型，通過用戶子程序urdfil讀取運算后的單元編號以及對應的節點信息，包括當前增量步、節點編號、坐標和位移等，裂紋尖端坐標可根據單元節點的水平集插值得到；通過指定J積分區域，判斷單元是否在積分區域內，并對落于積分區域內的單元節點賦予權函數；基于相互作用積分理論，構造輔助場并計算輔助場的應力應變，將真實場與輔助場的應力應變代入式(5)～式(11)分別計算得到J(1)、J(2)和KⅠ、KⅡ，并更新增量步直至計算完成。交互計算的流程見圖3，用戶子程序以及相互作用積分過程通過Fortran語言編寫相應代碼來完成。

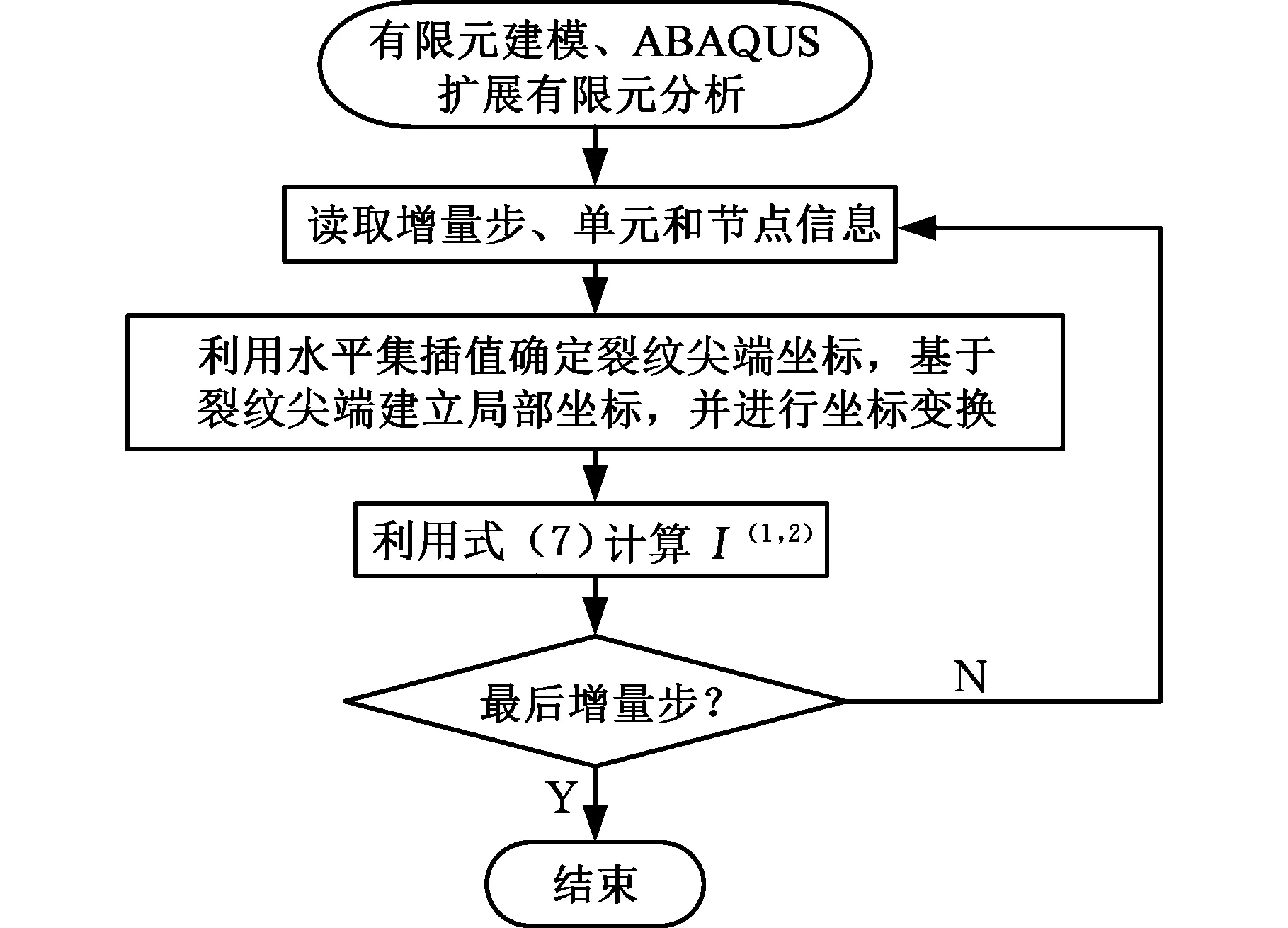
圖3 算法流程Fig.3 Algorithm flow

積分區域的指定是計算流程的一個關鍵步驟，圖4所示陰影部分為擬指定的積分區域，其中R為繞裂紋尖端圓的半徑(即積分半徑)，定義相對積分半徑為

Rk=R/r

(12)

式中，r為單元特征長度；S為單元面積。

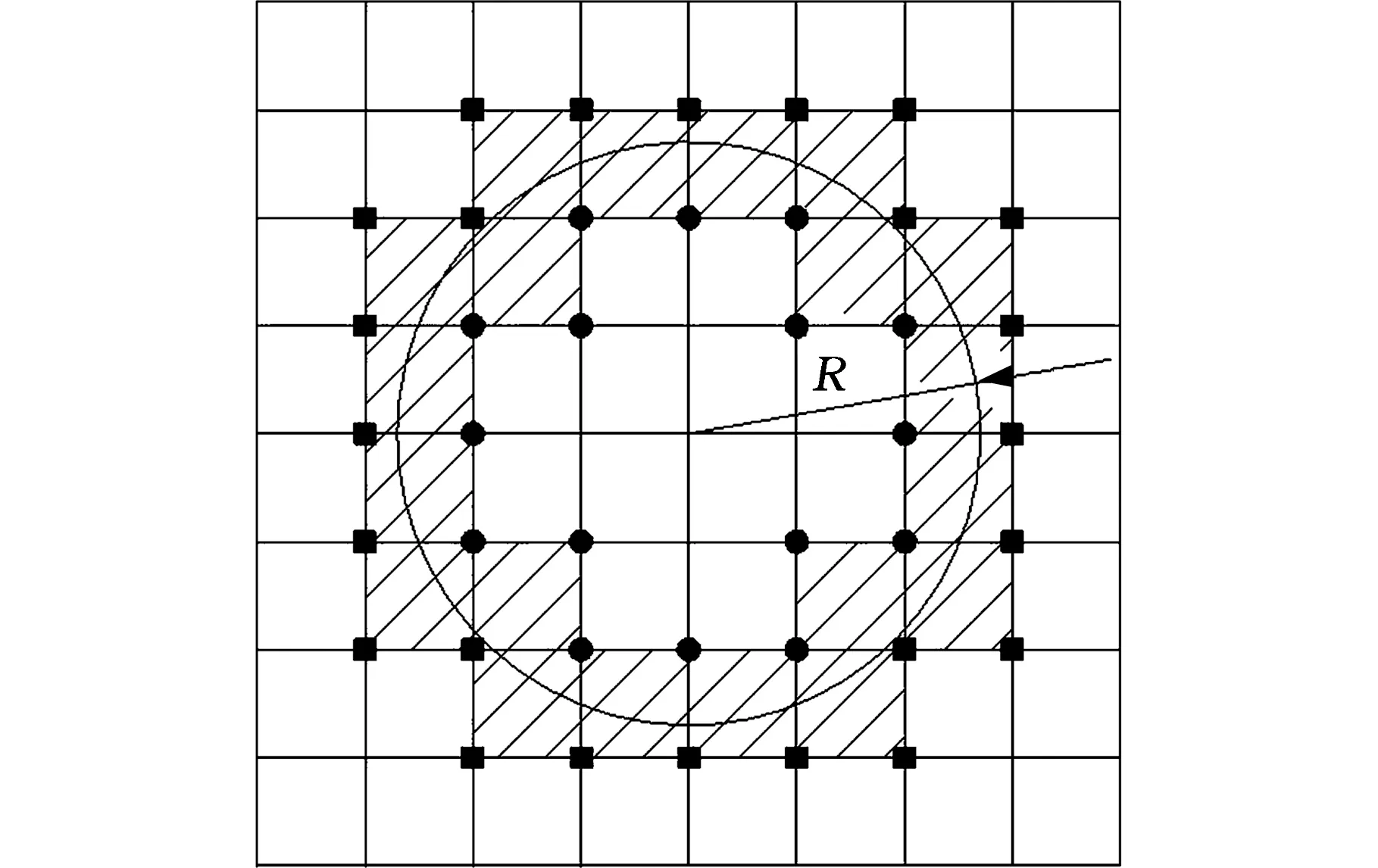
圖4 積分區域Fig.4 Integration area

當單元落于指定積分區域內時，為明確積分點的權函數q(x)，定義：當積分區域內節點到裂紋尖端的距離大于或等于半徑R時，節點權函數q(x)=1(x為方形節點)；當積分區域內節點到裂紋尖端的距離小于R時，其他節點權函數q(x)=0(x為圓形節點)。

3 應力強度因子計算精度與影響因素分析

3.1 不同裂紋擴展模式下應力強度因子的計算精度

受軸向拉伸載荷作用的中心裂紋平板試樣 和受集中載荷作用的三點彎曲試樣常用于Ⅰ型和Ⅱ型斷裂模式下的裂紋擴展規律的研究。分別制作滿足解析解獲得條件的中心裂紋平板標準試樣和三點彎曲標準試樣，并建立裂紋擴展規律分析的XFEM模型，如圖5所示。

圖5a所示為中心裂紋平板試樣，高度H=400 mm，寬度W=200 mm，上下兩端承受均布載荷σ=30 MPa的作用，裂紋長度定義為2a。圖5c所示為三點彎曲試樣，寬度W=20 mm，支撐點距作用點距離L=40 mm，受集中力FP=1 N的作用，裂紋長度定義為a。兩種試樣材料均為2024鋁合金，材料屬性如下[14]：彈性模量E=68 GPa，泊松比ν=0.33，主應力σmax=280 MPa。建立XFEM模型時，均采用四邊形平面應力單元、結構化網格劃分，兩種試樣的XFEM模型分別見圖5b和圖5d。

(a)中心裂紋平板幾何尺寸 (b)中心裂紋平板擴展有限元模型

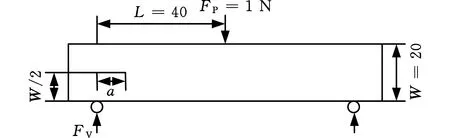
(c)三點彎曲試樣幾何尺寸

(d)三點彎曲試樣擴展有限元模型圖5 不同斷裂模式下應力強度因子的計算模型Fig.5 The calculation model of stress intensity factors under different fracture modes

由文獻[15]可知，受軸向拉伸載荷作用的中心裂紋平板的應力強度因子的理論計算表達式如下：

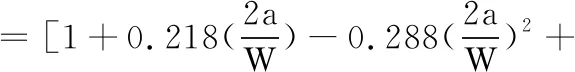
(13)

當L=2W時，三點彎曲試件的應力強度因子計算表達式如下：

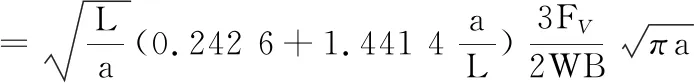
(14)

式中，FV為支撐點的支持力；B為板厚。

兩種試樣基于相互作用積分法的應力強度因子計算值與理論值對比結果以及計算誤差分別見表1和表2。由表1可知，在中心裂紋平板試樣的裂紋動態擴展過程中，程序計算值與理論值的偏差不超過3%；由表2可知，在三點彎曲試樣的裂紋動態擴展過程中，程序計算值與理論值的偏差不超過2%。這表明本文所提方法和程序合理，可準確地進行不同裂紋擴展模式下應力強度因子的計算。

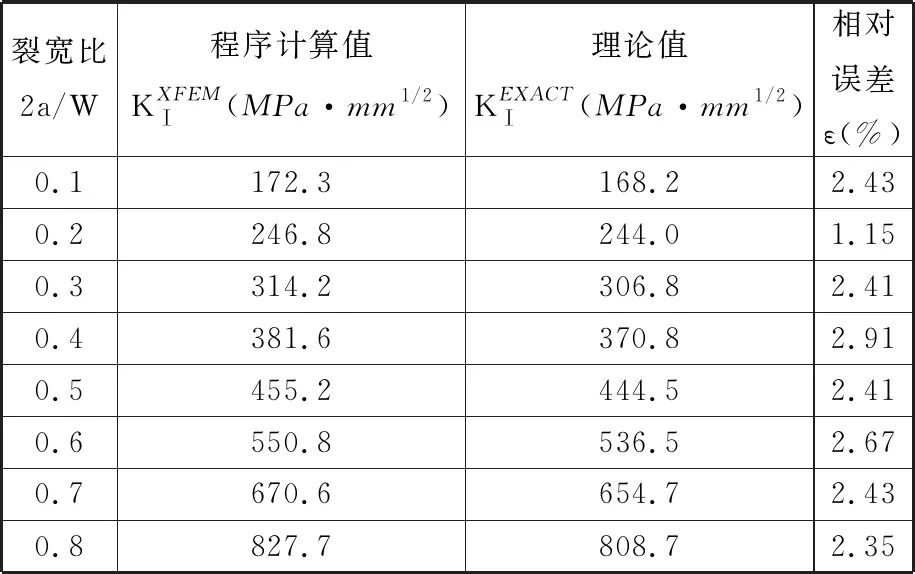
表1 中心裂紋平板計算誤差

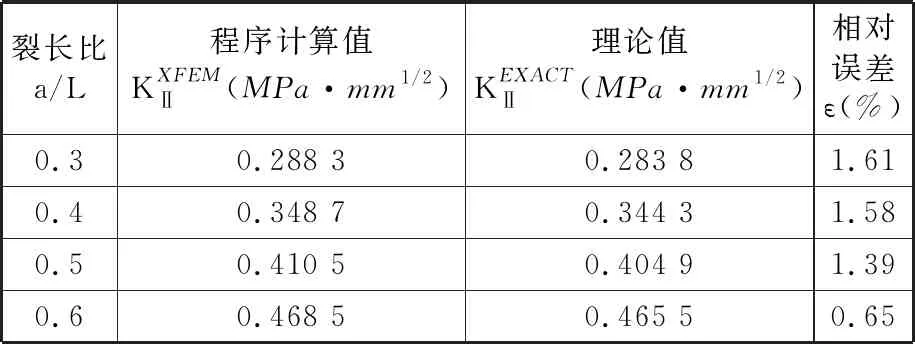
表2 三點彎曲試樣計算誤差

3.2 網格密度與積分半徑對計算精度的影響

積分半徑和網格密度是影響計算精度的主要因素，為確定合適的積分半徑與網格密度，研究了不同參數對應力強度因子計算精度的影響規律。

中心裂紋平板試樣和三點彎曲試樣在不同裂寬比(裂長比)、不同積分半徑下，應力強度因子計算值與理論值的相對誤差分別見圖6a和圖6b。由圖6可以看出，對于兩種試樣，當相對積分半徑Rk< 3時，計算誤差波動較大；當相對積分半徑Rk≥3時，中心裂紋平板試樣和三點彎曲試樣的應力強度因子計算誤差分別控制在3%和2%以內，滿足計算要求。

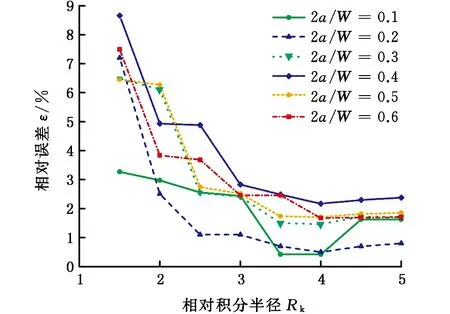
(a)中心平板裂紋試樣

(b)三點彎曲試樣圖6 積分半徑對應力強度因子的影響Fig.6 Effect of integral radius on stress intensity factors

對于圖6a所示的裂寬比為0.1的中心裂紋平板試樣，當相對積分半徑Rk=4.5時，對應的積分半徑R=20 mm， 積分邊界正好經過裂紋另一端點，裂紋尖端的應力奇異性導致應力強度因子過大，因此出現了應力強度因子突然增大的現象，但其計算精度仍然控制在3%以內。

為研究網格密度對計算精度的要求，定義網格密度因子為

m=r/l

(15)

式中，l為平板的特征長度。

中心裂紋平板試樣和三點彎曲試樣在不同裂寬比(裂長比)、不同網格密度下，應力強度因子計算值與理論值的相對誤差分別見圖7a和圖7b。由圖7可以看出，當m≥0.012時，隨著網格越密(即m越小)，計算誤差越小，求解精度越高；當m<0.012時，隨著網格越密，計算誤差越大。這是因為當網格過密時，積分區域是繞裂紋尖端很小的一個區域，計算值受裂尖奇異性的影響，誤差偏大。當網格密度因子m在0.012～0.016范圍內時，可得到較為準確的計算結果。

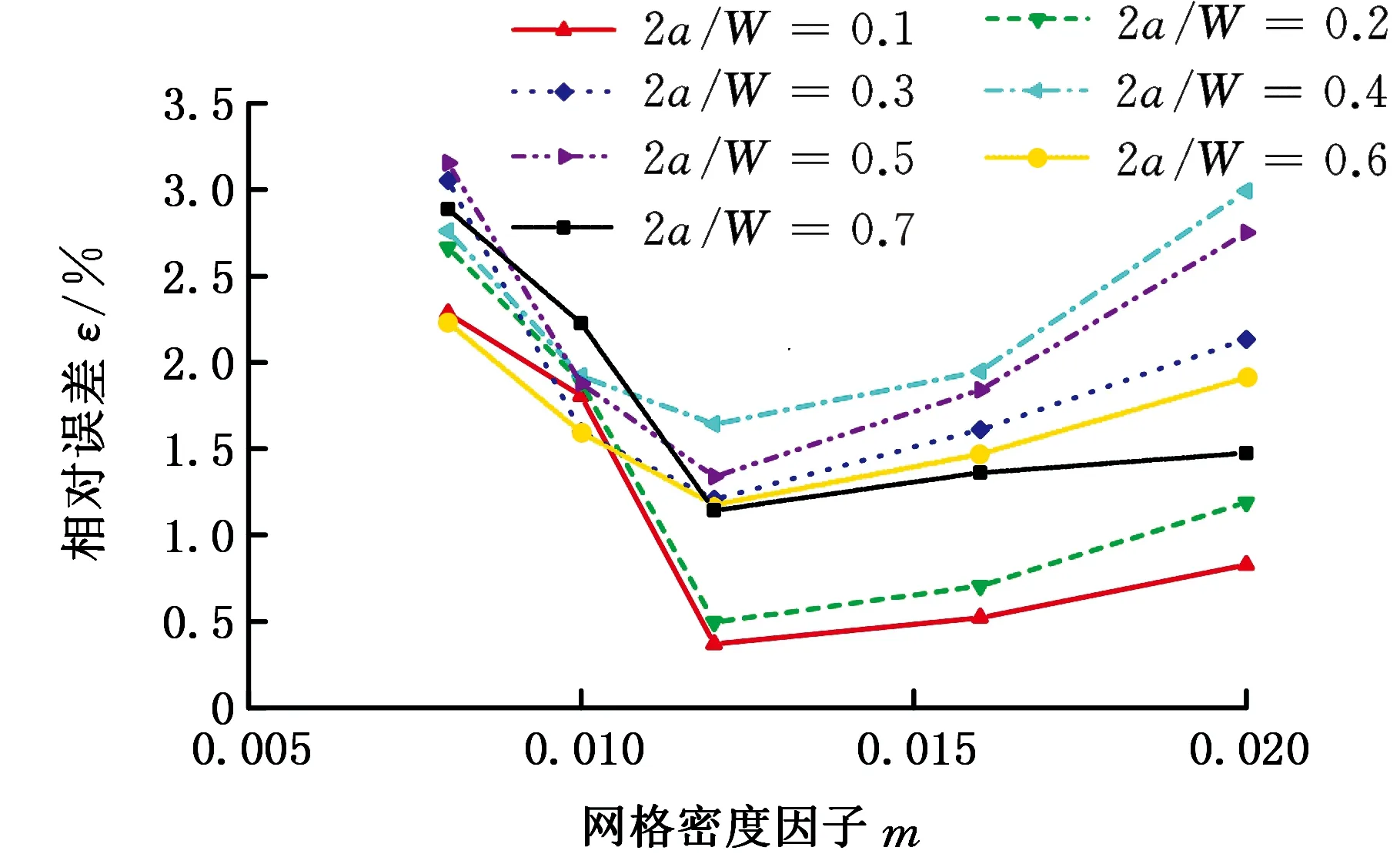
(a)中心裂紋平板試樣

(b)三點彎曲試樣圖7 網格密度對應力強度因子的影響Fig.7 Effect of mesh density on stress intensity factors

4 典型試樣動態裂紋擴展應力強度因子計算與剩余壽命預測

非標準試樣動態裂紋擴展過程應力強度因子沒有解析解，無法直接驗證應力強度因子計算結果的準確性。將應力強度因子代入Paris公式實現各類試樣剩余壽命的預測，是應力強度因子的一個典型應用，同時也可間接地驗證動態裂紋擴展應力強度因子計算的準確性。

Paris公式計算疲勞裂紋擴展的壽命模型可表示為[16]

da/dN=C(ΔK)n

(16)

ΔK=Kmax-Kmin

式中，N為循環次數；C、n為材料常數，本文所用參數由文獻[17]給出，C=1.484×10-10mm/周次、n=2.761；ΔK為應力強度因子的變化，MPa·mm1/2；Kmax、Kmin分別為循壞載荷下應力強度因子的最大值和最小值。

本研究的對象為非標準帶孔單邊裂紋擴展試樣，其形狀和尺寸見圖8a。其中，試樣高度H=200 mm、寬度W=100 mm，圓孔直徑為10 mm，試樣預制初始裂紋長度a=17 mm。試樣受軸向應力均值為36 MPa、應力比為0.1的循環載荷σ作用，試驗在MTS 810材料試驗機上進行，裂紋擴展長度采用顯微鏡直讀法來獲取，測量誤差不超過0.01 mm，見圖8b。在ABAQUS軟件中利用本文所提方法及程序建立非標試樣裂紋擴展的XFEM模型(圖8c)并計算應力強度因子，相關材料參數同前文2024鋁合金的材料屬性參數。建模時的網格密度因子為0.012，相對積分半徑為3。

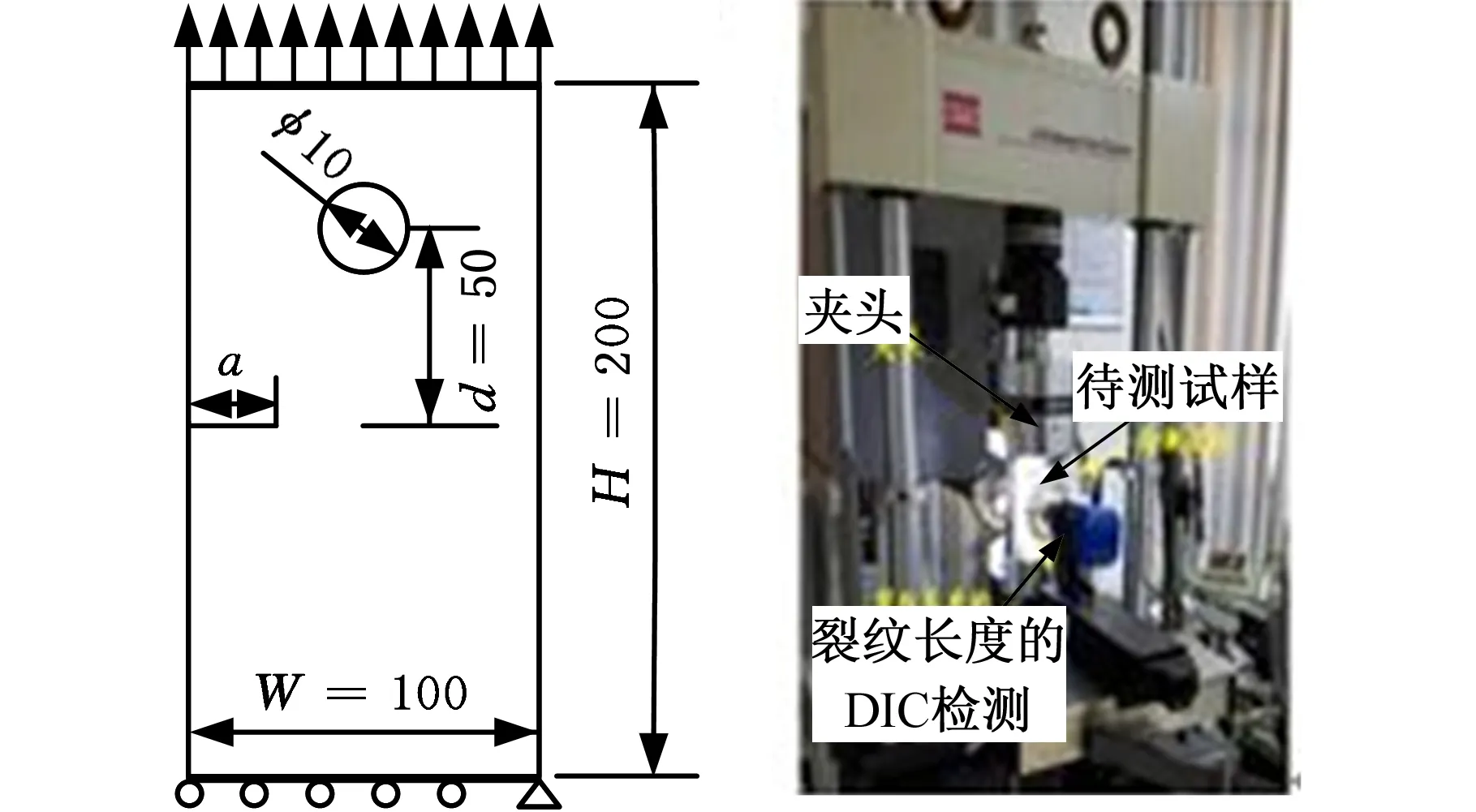
(a)試樣幾何尺寸 (b) 裂紋擴展試驗

(c)XFEM模型圖8 單邊帶孔平板模型Fig.8 Single side hole plate model

圖9所示為裂紋擴展過程的仿真計算結果與試驗實測結果，可以看出，仿真計算與試驗測定的裂紋擴展路徑基本一致。圖10所示為計算得到的動態裂紋擴展應力強度因子變化規律，可以看出，應力強度因子KⅠ隨著裂紋的擴展不斷增大；應力強度因子KⅡ要小于KⅠ兩個數量級以上，這表明單邊裂紋帶孔平板疲勞擴展以Ⅰ型為主，與實際情況相符(圖9)。

(a)疲勞仿真結果 (b)疲勞試驗結果圖9 疲勞仿真與試驗的擴展路徑Fig.9 Extended path of fatigue simulation and test

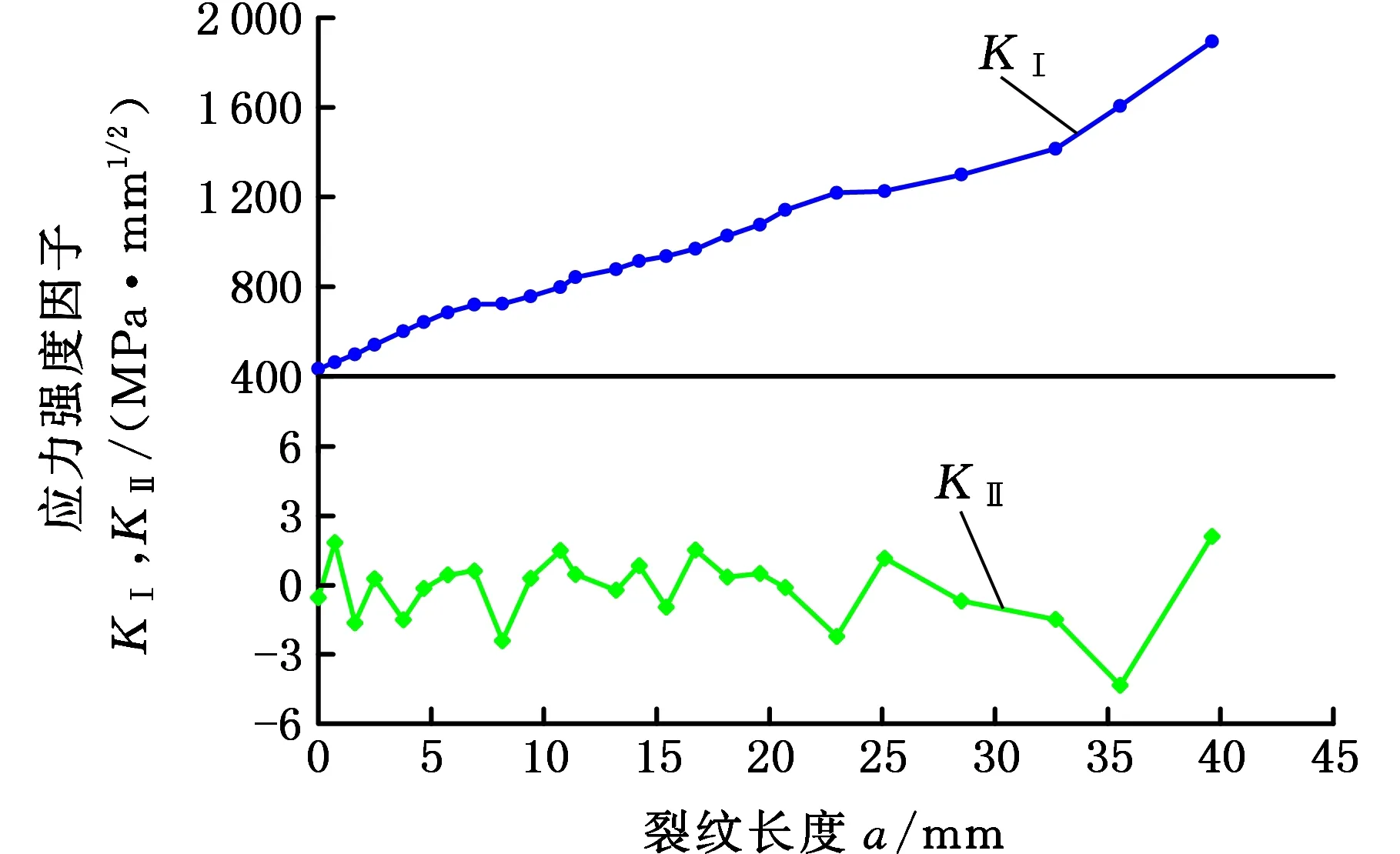
圖10 應力強度因子Fig.10 Stress intensity factors

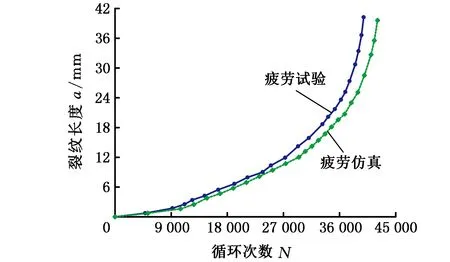
(a)疲勞裂紋擴展a-N曲線

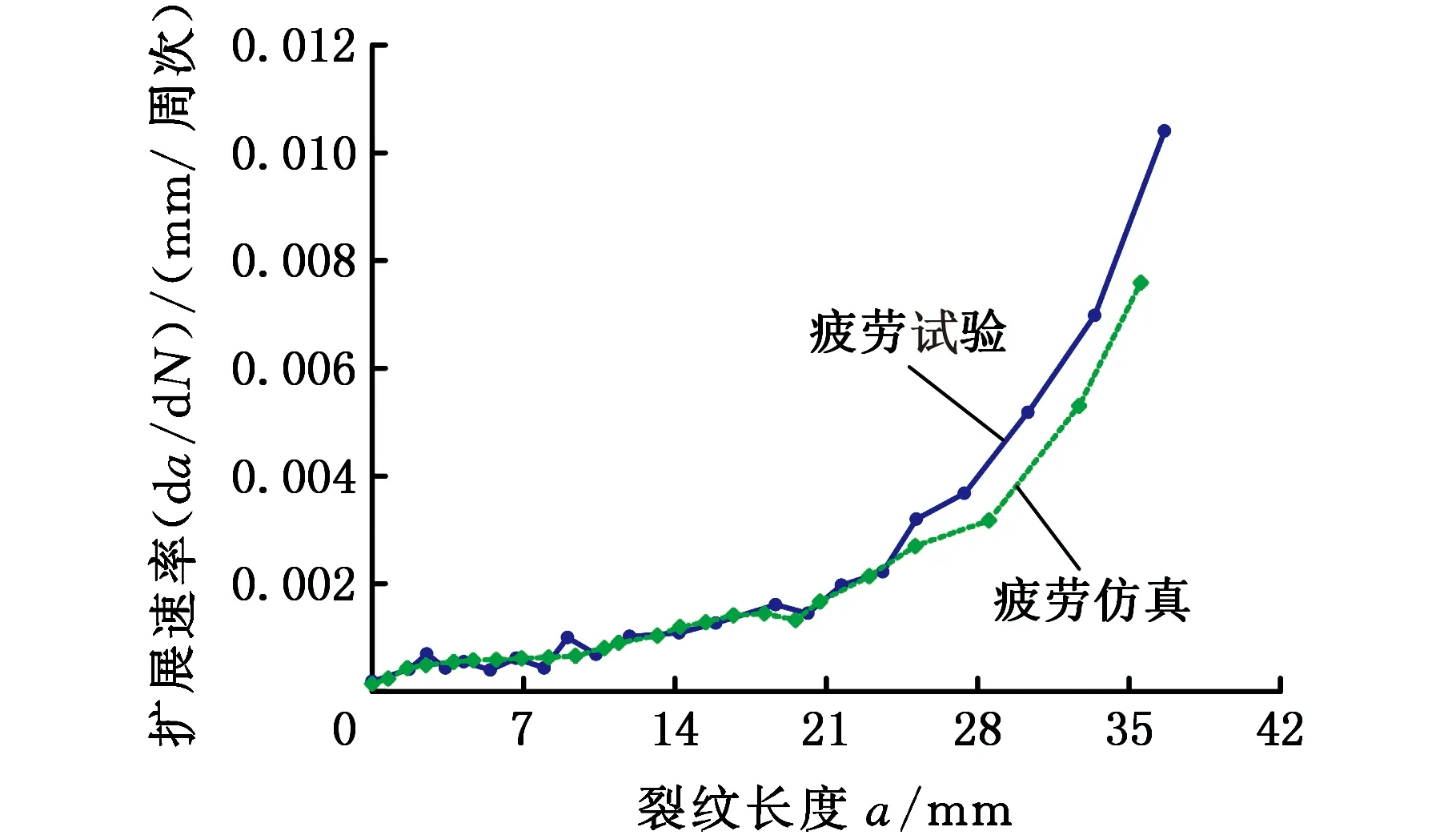
(b)疲勞裂紋擴展速率da/dN曲線圖11 單邊帶孔平板試樣的疲勞壽命預測Fig.11 Fatigue life prediction of single side hole plate specimens

單邊帶孔平板試樣的疲勞壽命預測結果見圖11。圖11a為依據應力強度因子變化規律所計算得到的試樣a-N曲線，可以看出，理論預測與試驗檢測結果具有較好的一致性，試樣疲勞裂紋擴展的預測壽命與實測壽命分別為42 085周次和39 857周次，兩者相差5.3%，在許用誤差范圍內。圖11b為疲勞裂紋擴展速率da/dN曲線 ，可以看出，由應力強度因子計算得到的擴展速率與試驗得到的疲勞擴展速率基本一致，進一步驗證了應力強度因子的計算精度能夠滿足工程要求。

5 結論

(1)在ABAQUS軟件中建立了典型試樣動態裂紋擴展的XFEM模型；基于相互作用積分方法,通過Fortran語言編制用戶子程序，實現了動態裂紋擴展XFEM模型應力強度因子的計算。

(2)中心裂紋平板標準試樣和三點彎曲標準試樣的動態裂紋擴展中應力強度因子計算值與理論值的對比分析結果表明：所提方法與所編制的程序可用于Ⅰ型、Ⅱ型裂紋擴展應力強度因子的準確計算，計算誤差分別小于3%和2%。

(3)探討了網格密度和積分半徑對計算精度的影響規律，結果表明：當網格密度因子為0.012～0.016、相對積分半徑Rk=3時，計算結果收斂于穩定值，計算誤差控制在3%內。

(4)利用所提方法與程序對非標帶孔單邊裂紋擴展試樣的動態應力強度因子進行了計算，基于Paris公式預測了非標準試樣的疲勞裂紋擴展壽命。疲勞裂紋擴展實測結果驗證了模型與所提方法的正確性,仿真值與試驗值的偏差為5.3%，在許用誤差范圍內。