基于三維成形極限應力圖的AA6061擠壓管材成形性能分析
朱良金 陳孟杰 王 威 杜 飛 董國疆
燕山大學河北省特種運載裝備重點實驗室,秦皇島,066004
0 引言
高強鋁合金板殼材料在室溫條件下塑性較差[1],難以成形復雜形狀零件,容易出現頸縮和破裂失穩現象,一般應用溫熱成形[2-3]或固溶處理后立即成形等工藝方法實現此類板殼材料的塑性變形[4]。大部分高強鋁板殼材料在加熱或熱處理后[5-6],強度和硬度大幅降低,延伸性能大幅提高,脆性斷裂特征弱化,韌性斷裂特征增強,從而有利于板殼塑性成形。同時,軟化作用使板殼面內屈服應力大幅減小[7],厚向應力相對于面內應力的占比大幅提高,這使得在一些金屬板殼在液壓脹形、快速氣脹、黏性介質或顆粒介質壓力成形等工藝過程中不能再忽略厚向應力的影響[8-9]。
在內高壓成形和軟模脹形等工藝中,傳力介質與被加工表面產生強烈壓力作用,使得厚向應力對板殼成形性能產生了一定的影響。為此,國內外諸多學者采用不同的改進M-K模型,結合不同屈服準則和硬化規律,推導和修正理論成形極限圖,并對不同材料成形性能進行了深入的研究。ZHANG等[10-11]假設靜水壓力對塑性成形沒有影響,結合Yld2003屈服準則和M-K模型,從理論上獲取了考慮厚向應力的AA6111-T43板材多種成形極限曲線,研究發現應變成形極限曲線(forming limit curve,FLC)、等效應變FLC和具有不同預應變的FLC均隨著厚向應力的增大而顯著上升,結果表明厚向應力可提高板材成形性能。LANG等[12]結合Hill 48準則構建了考慮厚向應力的擴展M-K模型,研究了5A06板材溫液壓成形中變形溫度和厚向應力對應變成形極限圖(forming limit diagram,FLD)的綜合影響,結果表明:隨著厚向應力絕對值的增大,5A06板材的FLC向右上偏移。YANG等[13]結合韌性斷裂準則與厚向應力的修正M-K模型研究5A06-O鋁合金板材FLD,與傳統M-K模型對比結果顯示,修正模型預測的FLD與實驗值更加接近,厚向應力使板材的成形極限顯著提高。MIRFALAH-NASIRI等[14]依據Yld2011屈服準則和改進的M-K模型繪制出AA3104-H19板材的FLC,以及成形極限應力曲線(forming limit stress curve,FLSC)和延伸成形極限應力圖(extended forming limit stress diagram,XFLSD),研究表明基于Yld2011預測的板材各向異性塑性行為與實驗數據有很好的一致性,在平面應變狀態下極限應變增大了35%。上述研究通過理論和實驗論證了厚向應力對板殼成形極限的影響不可忽視,特別是對成形窗口較小的鋁合金板材的影響更為突出。此外,應變路徑的改變對成形極限應力圖(forming limit stress diagram,FLSD)的結果幾乎沒有影響,故FLSD在汽車車身覆蓋件和飛機鈑金零件拉深等多道次成形工藝中有廣泛的應用價值。在多道次板料成形有限元分析中,采用FLSD作為成形的數值模擬時的成形極限判據,可以得到較為精確的模擬結果[15-16]。
基于上述分析,本文將考慮厚向應力影響的M-K模型與Hill48屈服準則結合,推導三維成形極限應力圖(three-dimensional forming limit stress diagram, 3D-FLSD),并將其應用于AA6061擠壓管材固溶水淬后冷脹形的成形性能分析。利用3D-FLSD獨立于應變路徑的特點,為高強鋁合金板殼構件的結構設計、成形性能分析和工藝路線制定提供便捷、精確的判據,以滿足當前精確塑性成形工藝發展的需求。
1 考慮厚向應力的M-K模型
1.1 數值模型的建立
M-K模型是預測板殼成形極限的經典理論方法,假設該模型在板面垂直于σ1方向上存在初始凹槽,這一凹槽成為集中失穩發生的區域,見圖1。其中,σ1、σ2、σ3分別為第一、二、三主應力,ta0、tb0分別為a區和b區的初始厚度,ta、tb分別為a區和b區的板殼厚度。當板材兩端受到拉伸作用時,凹槽處變形集中,進而產生斷裂。假設在變形過程中,a、b區域中的厚向應力(即第三主應力σ3)不受面內應力的影響,且厚向應力的數值相同[12],考慮厚向應力影響的M-K模型如圖1所示。
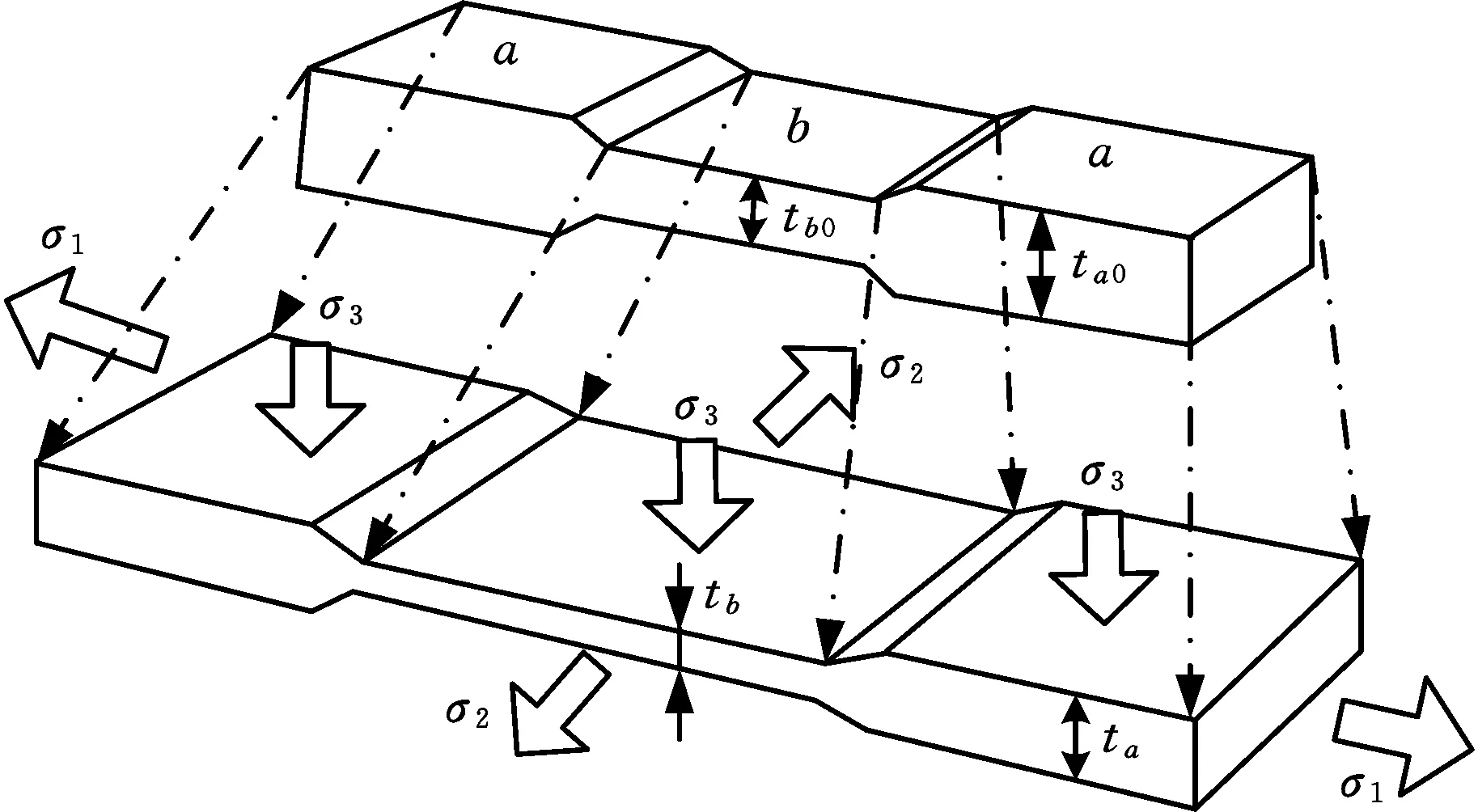
圖1 M-K模型示意圖Fig.1 Schematic of M-K model under 3D stress condition
在受載變形過程中,每一瞬間a區第二主應變增量dε2a和b區第二主應變增量dε2b的數值相等,即
dε2a=dε2b=dε2
(1)
第一應力主軸方向的力平衡條件滿足:
σ1ata=σ1btb
(2)
M-K模型滿足體積不變條件。若管材塑性變形前后的體積不變,則第一、二、三主應變增量滿足:
dε1+dε2+dε3=0
(3)
在變形過程中,a區和b區的第三主應力獨立于平面應力,且數值相等,即
σ3a=σ3b
(4)
忽略板材彈性變形,假設初始狀態下a區和b區的應變均為零,則初始厚度不均度定義為
(5)
基于Hill 48屈服準則,可將三維主應力條件下的屈服函數表示為
(6)
r=H/F=H/G
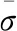
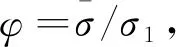
(7)
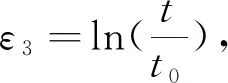
(8)
聯立式(2)和式(4)可得
(9)
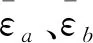
(10)
(11)
(12)
(13)
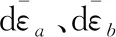
聯立式(12)和式(13)可得
(14)
根據材料本構方程
σ=Kεn
(15)
式中,σ為真實應力,MPa;K為強度系數,MPa;ε為真實應變;n為應變硬化指數。
將式(10)~式(13)聯立可得
(16)
1.2 模型解析
基于M-K模型的變形分析,第三主應力σ3的作用通過參數γ來體現。求解步驟如下。
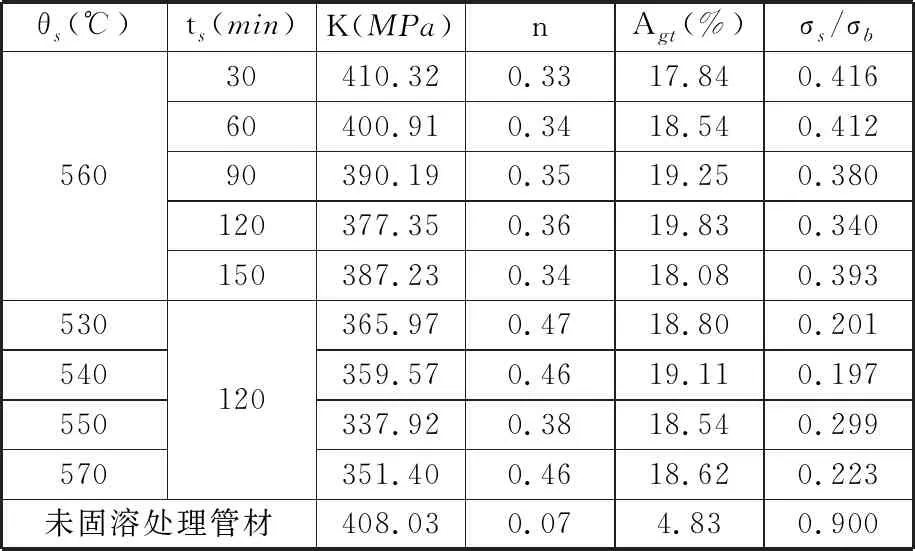
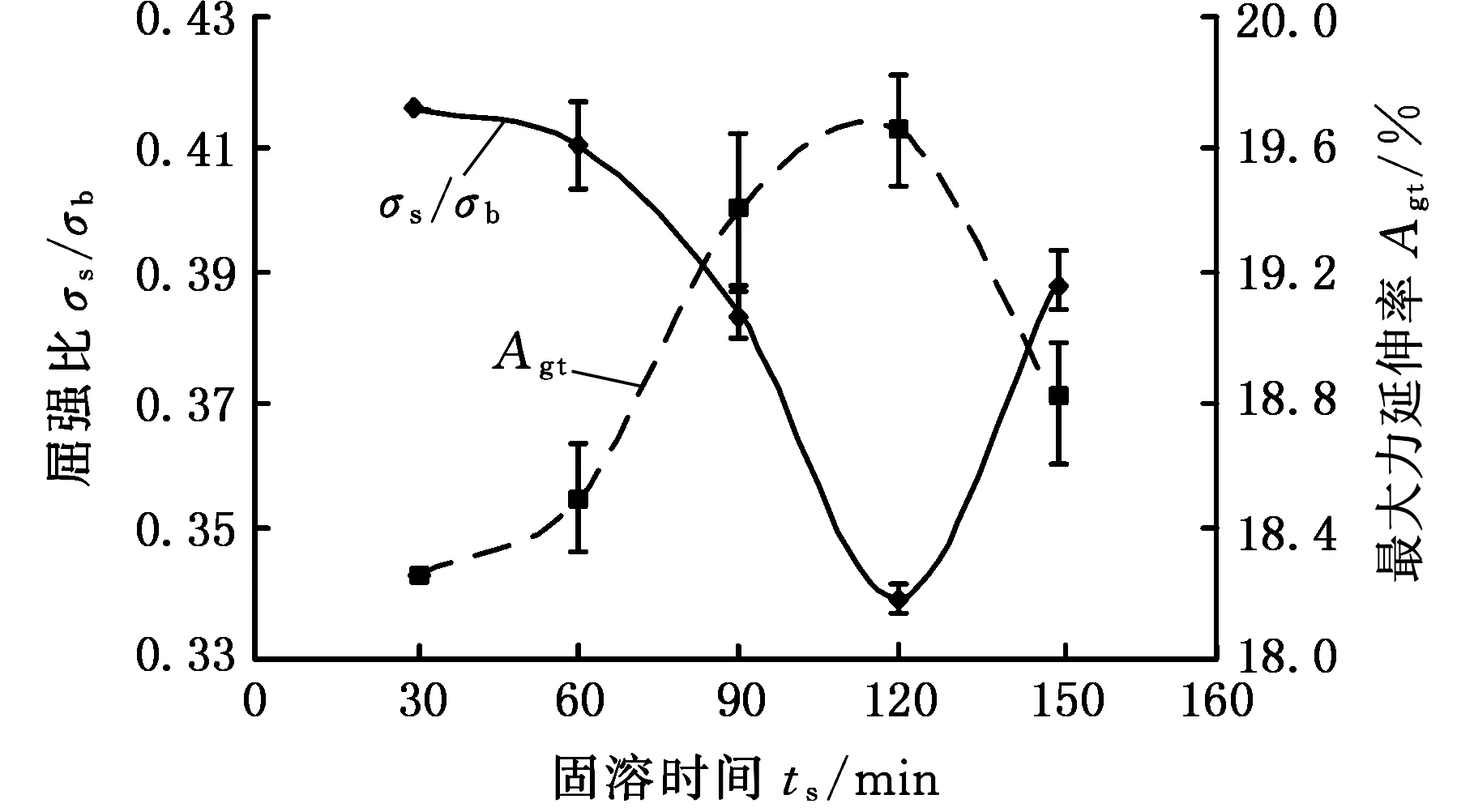
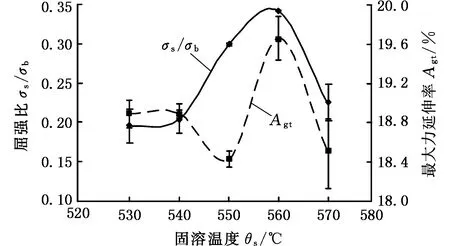
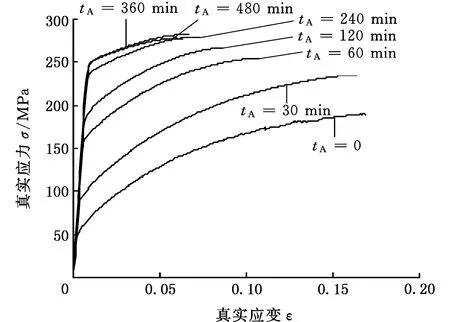
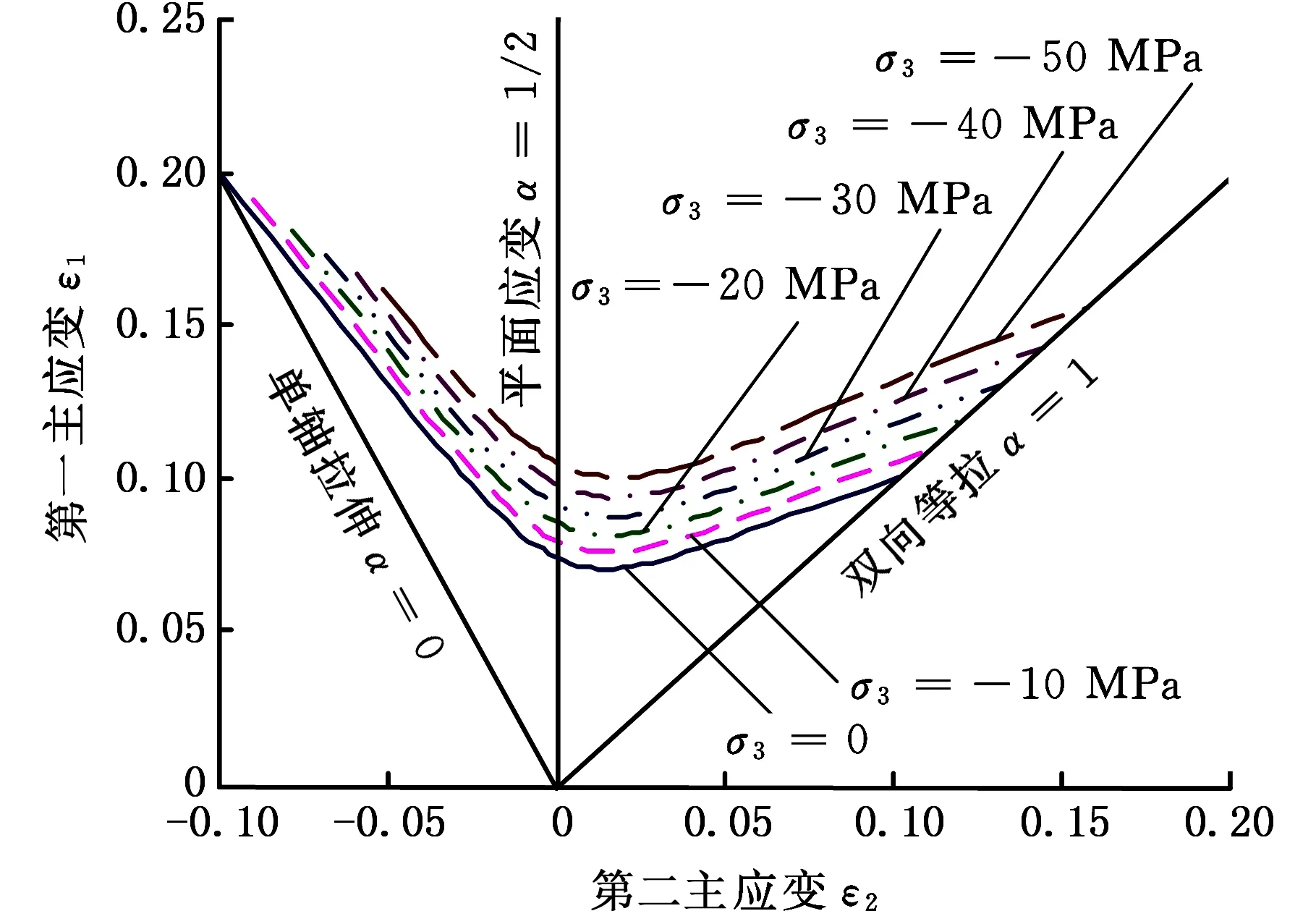
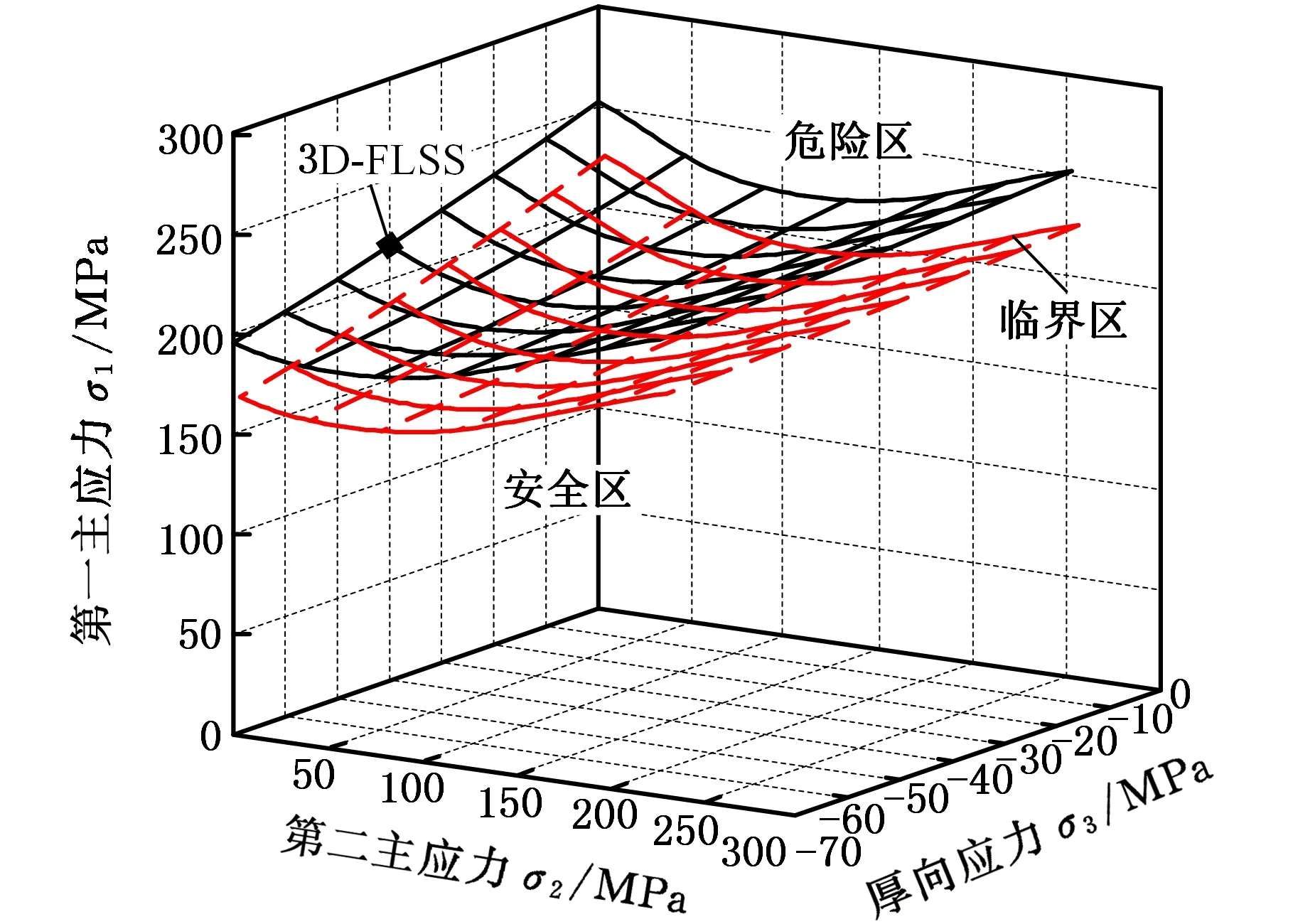
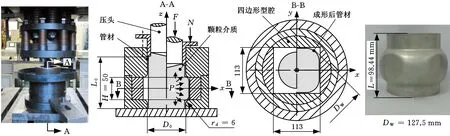
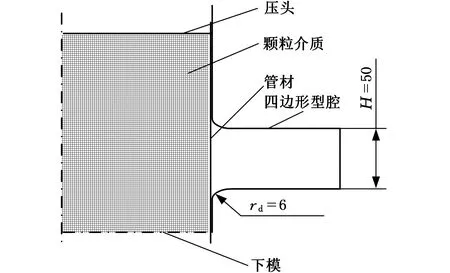
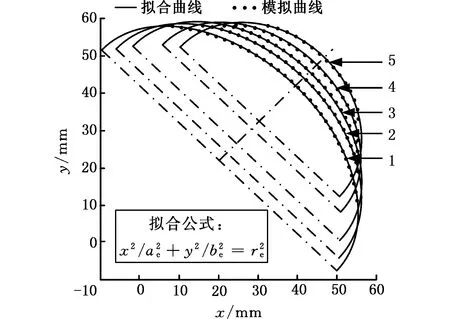
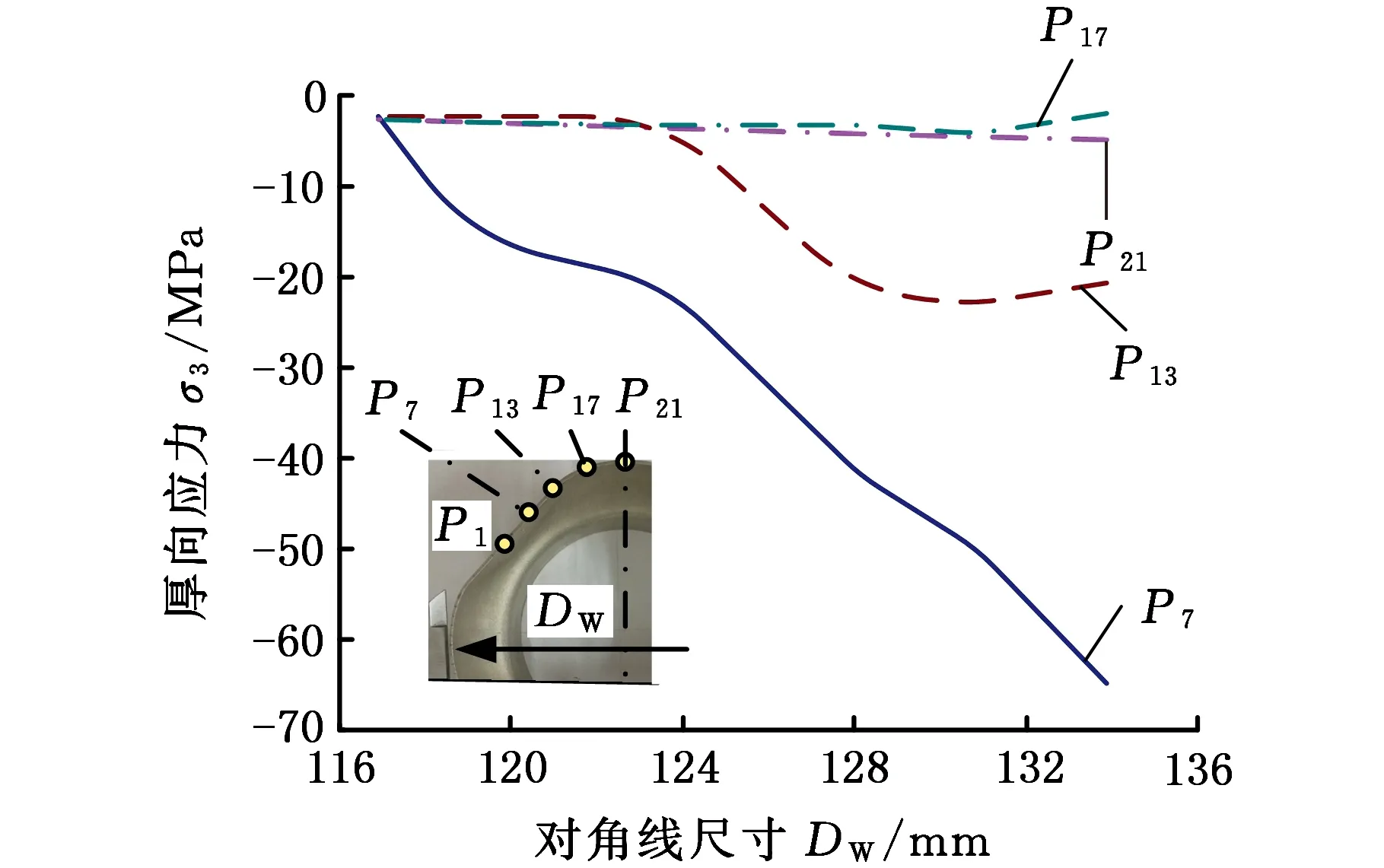
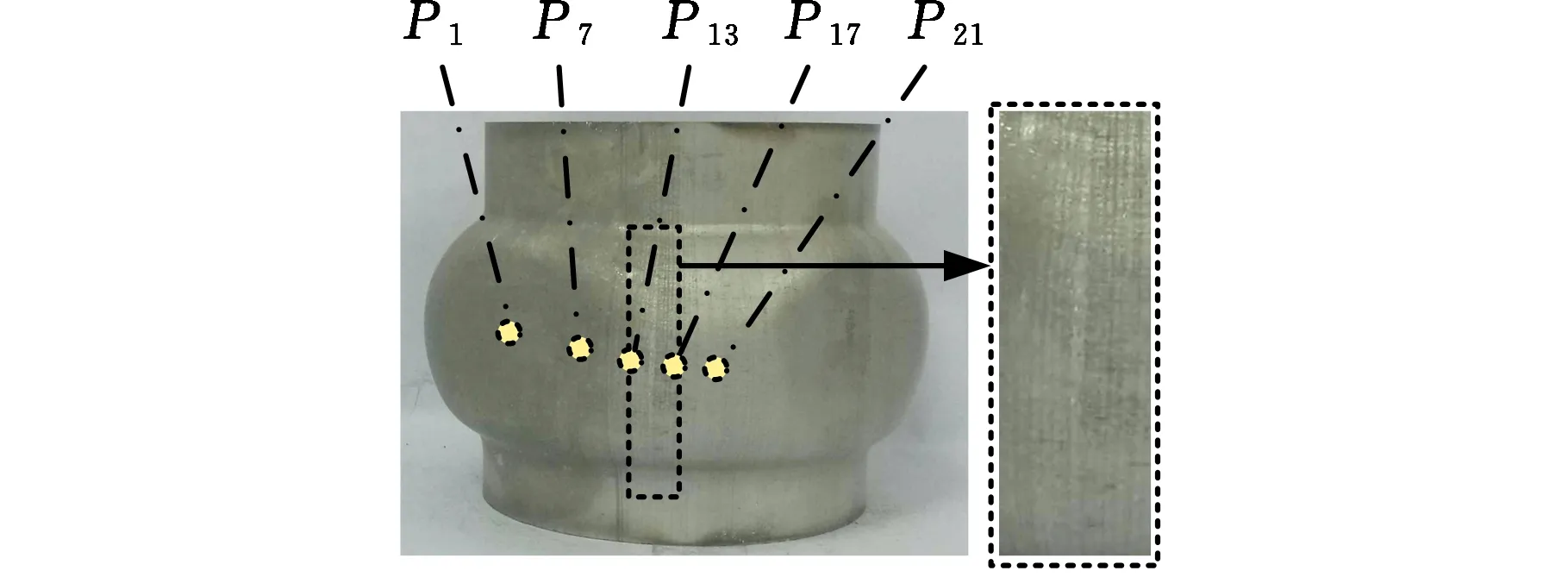
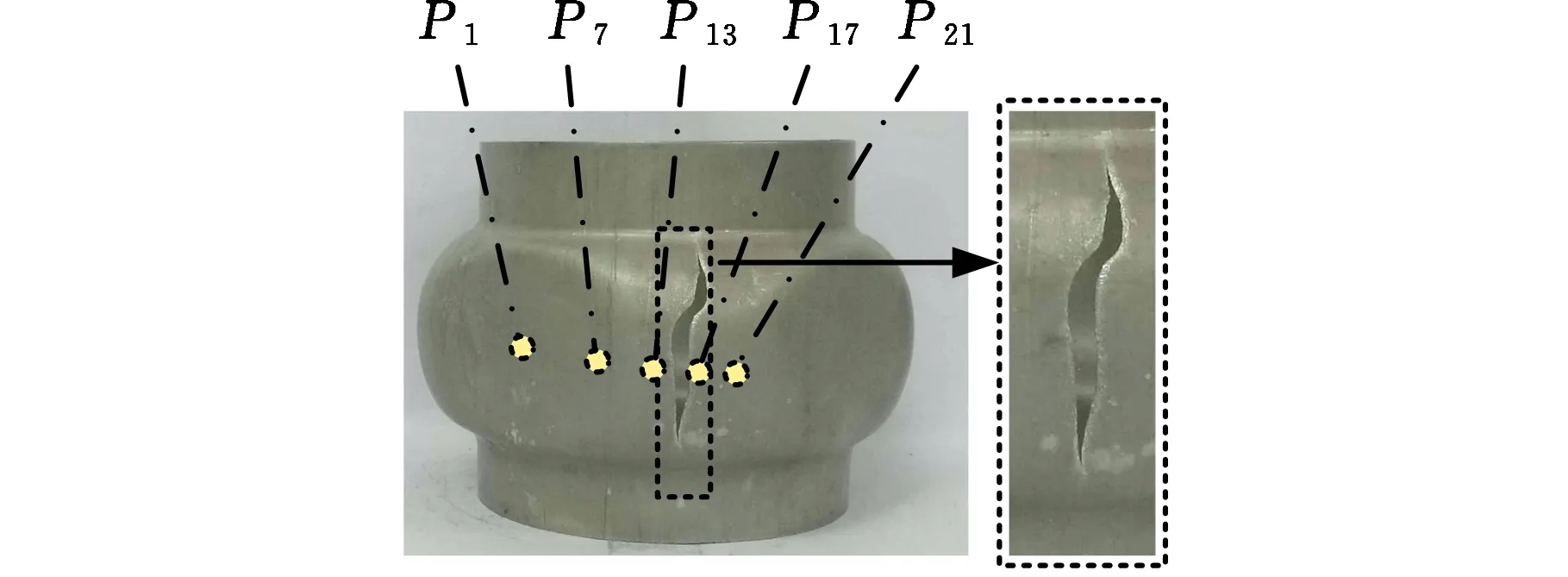
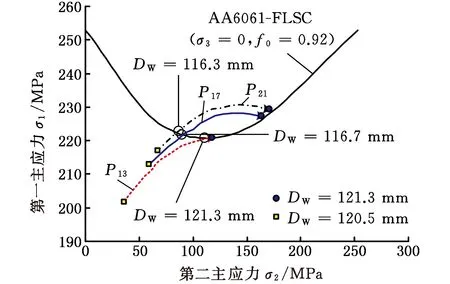
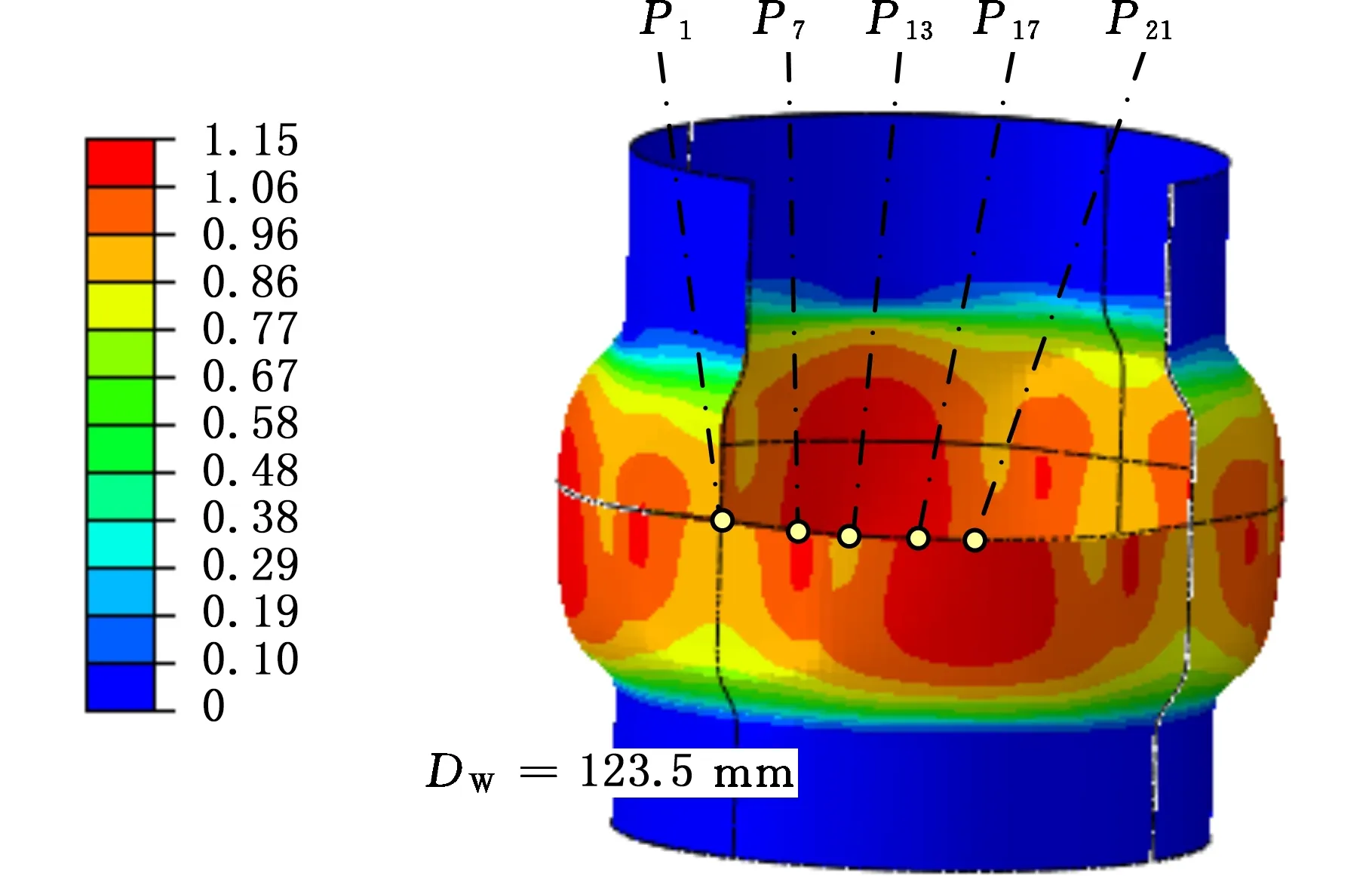
(1)設定溝槽區域(b區)第一主應力方向的應變增量值dε1b=0.005,且在變形過程中保持不變。根據dε1a (2)根據Drucker公設和等效塑性功原理,將式(7)寫為 (17) 引入參數 (18) (19) 可得 (20) (21) (3)令a區和b區的第三主應力σ3為定值,設定a區應力比參數αa(0≤αa≤1)和γa。由式(7)、式(20)和式(21)可得 (22) (23) (24) 進而可分別得 dε2a=ρadε1a (25) (26) 聯立式(3)和式(25)得 dε3a=-(1+ρa)dε1a (27) (4)聯立公式得到b區參數ρb、γb、αb、βb和φb的表達式。 聯立式(1)、式(18)和式(25)得 (28) 由式(9)、式(20)及式(7)依次得 γb=γaf0exp(ε3b-ε3a)=γaf (29) (30) (31) 由式(21)得 (32) (33) 聯立式(3)和式(25),可得 dε3b=-dε1b-ρadε1a (34) (35) (6)運用Newton-Raphson迭代法,a區第一主應變增量新值可表示為 (36) (37) (38) 基于以上推導,若已知板殼材料的力學性能參數,給定應力比及第三主應力數值,即可通過數值迭代計算獲取理論3D-FLSD。 本文采用西南鋁業AA6061擠壓管材(公稱厚度δ0=1.2 mm、外徑D0=100 mm),參照GB228—2002金屬拉伸標準,自行設計管材軸向切取拉伸試樣。在SX-G16103馬弗爐中進行固溶處理,固溶溫度θs為530 ℃、540 ℃、550 ℃、560 ℃和570 ℃,保溫時間ts為30 min、60 min、90 min、120 min和150 min。固溶處理后,在20 ℃恒溫水浴鍋中進行淬火處理,試樣轉移時間控制在5 s以內。測試在Inspekt-Table100電子萬能試驗機上完成,應變速率為0.001 s-1。試驗獲得的AA6061擠壓管材材料性能參數見表1。其中,Agt為最大力延伸率,σs/σb為屈強比。不同固溶工藝對AA6061擠壓管屈強比和最大力延伸率的影響見圖2。 表1 不同固溶工藝下AA6061擠壓管材料性能參數 (a)恒定固溶溫度為560 ℃ (b)恒定固溶時間為120 min圖2 不同固溶工藝對AA6061擠壓管屈強比和最大力延伸率的影響Fig.2 Effect of solution treatment process on σs/σb and Agt of AA6061 extruded tube 屈強比和延伸率是評價材料成形性能優劣的重要指標。由表1和圖2可知,AA6061擠壓管材的室溫延伸率極低,最大力延伸率Agt=4.83%,難以滿足一般形狀零件的成形要求。經固溶(θs=560 ℃,ts=120 min)水淬后,Agt可達到19.83%,較未經固溶處理(no solution treatment, NST)管材的Agt提高了3倍多;固溶后管材的屈服強度σs=53.7 MPa,較NST管材的屈服強度下降了81.4%,固溶后管材的抗拉強度σb=189.9 MPa,較NST管材的抗拉強度下降了40.8%,固溶后管材的屈強比σs/σb由NST管材的屈強比0.900降低至0.197~0.416。固溶水淬使管材延伸率大幅提高,強度降低,有利于管材脹形率和定形性能的提高。當固溶條件為θs=560 ℃、ts=120 min時,AA6061擠壓管材的塑性成形性能接近最優。 將管材試樣固溶(θs=560 ℃,ts=120 min)水淬后進行人工時效,一般選取噴涂烘烤溫度θA=180 ℃,采用涂裝工藝實現時效強化作用,并給定不同時效時間tA,經過人工時效后將合金空冷。應變速率為0.001 s-1時,不同人工時效條件下的試驗結果見圖3,可以看出,隨著時效時間tA的延長,管材強度增強,Agt減小;當人工時效條件為θA=180 ℃、tA=360 min時,固溶后的管材屈強比σs/σb=0.88,Agt=5%,其管材性能與NST管材的性能基本相同。 圖3 不同人工時效條件下AA6061的真實應力應變曲線(θs=560 ℃,ts=120 min,θA=180 ℃)Fig.3 Effect of aging treatment process parameters on true stress-strain curves of AA6061(θs=560 ℃,ts=120 min,θA=180 ℃) 圖4所示為固溶處理對AA6061擠壓管斷裂形貌的影響。由圖4a可以看出,對于未經固溶處理的AA6061管材,斷面存在少量淺的韌窩和解理臺階,高倍下觀察顯示斷口存在大量撕裂棱,結果表明原始(NST)管材的室溫塑性變形能力較差。由圖4b可以看出,試樣固溶(θs=560 ℃,ts=120 min)水淬后,斷口出現大量等軸韌窩,且較NST管材的韌窩加深,呈現韌性斷裂特征,即宏觀變形表現為塑性顯著增強,斷裂方式由脆性斷裂過渡為韌性斷裂。由圖4c可以看出,拉伸試樣經固溶(θs=560 ℃,ts=120 min)水淬后再經人工時效(θA=180 ℃,θA=360 min),斷口處韌窩出現明顯的滑移特征,沿同一方向明顯拉長呈拋物線狀,即撕裂韌窩類型。 (a)未經固溶處理 (b)固溶(θs=560 ℃,ts=120 min)水淬 (c)固溶(θs=560 ℃,ts=120 min)水淬后人工時效(θA=180 ℃,tA=360 min) 圖4 固溶處理對AA6061擠壓管斷裂形貌的影響Fig.4 Effect of solution treatment process parameters on fracture morphology of AA6061 extruded tube 參見文獻[4,17],將AA6061擠壓管材固溶(θs=560 ℃,ts=120 min)水淬后的試樣材料性能參數代入已建立的修正M-K模型中,通過實測與理論推導計算相結合的方式,標定固溶(θs=560 ℃,ts=120 min)水淬后AA6061擠壓管材的初始厚度不均度f0=0.92。 不同厚向應力σ3條件下的AA6061擠壓管材理論FLC見圖5。厚向應力的增大能夠提高板材的成形極限值,表現為理論FLC在主應變空間中整體沿雙向等拉線向右上偏移;與平面應力狀態(σ3=0)相比,考慮厚向應力的理論FLC在第二象限(拉-壓應變狀態)的抬升較小,而在第一象限(拉-拉應變狀態)的抬升較大。由此可知,對于成形窗口較小的鋁合金板殼材料的成形性能分析應考慮厚向應力的影響。 圖5 不同厚向應力條件下AA6061擠壓管成形極限圖(f0=0.92)Fig.5 FLD of AA6061 extruded tube under different thickness normal stress conditions(f0=0.92) 利用圖5中的數據容易得到AA6061管材的三維成形極限應力曲面(three-dimensional forming limit stress surface,3D-FLSS),為引入安全余量,一般將成形極限數值向下偏置10%[18],偏置3D-FLSS以下區域為安全區,3D-FLSS以上區域為危險區,兩者之間為臨界區,見圖6。 圖6 AA6061擠壓管三維成形極限應力圖(θs=560 ℃,ts=120 min)Fig.6 3D-FLSD of AA6061 extruded tube(θs=560 ℃,ts=120 min) 本文通過“固溶水淬處理+顆粒介質脹形+人工時效”處理的工藝流程試制四方截面管件。其中,顆粒介質壓力成形技術是管狀構件內高壓成形技術的拓展,采用固體顆粒介質代替現有高壓成形工藝中液體或氣體的作用,利用顆粒介質耐高壓性、易流動性和易密封等特點,實現管狀構件內高壓成形[19-20],見圖7。其中,H為型腔高度,rd為凹模圓角。對管件脹形過程進行仿真與試驗研究,分析管件變形狀態,結合理論FLSD和3D-FLSD對破裂失穩趨勢進行判定和分析。 運用ABAQUS/Explicit分析模塊和擴展Drucker-Prager線性模型仿真分析AA6061擠壓管材固體顆粒脹形[21]。根據本課題組測試獲取的顆粒介質材料性能參數[22-23],選用5號非金屬顆粒(non-metallic granules,NMG)作為傳壓介質用于鋁合金管件脹形。5號NMG粒徑在0.117~0.140 mm之間,洛氏硬度達到48 HRC ~55 HRC,外觀光潔圓整,非黏性材料(黏聚力為零),得到常溫條件下5號NMG的擴展Drucker-Prager材料模型參數,見表2。 為反映厚向應力效應,有限元分析模型的建立采用三維實體單元,厚度方向設置7個節點,將AA6061管材模型分為6層,由內至外依次為1~6層,AA6061管材的材料參數依據本文試驗給定。模具與管材間接觸摩擦因數設定為0.2,模具與介質間接觸摩擦因數設定與接觸壓力相關(表2),仿真模型如圖8所示。 采用AA6061擠壓管材(初始厚度δ0=1.20 mm,直徑D0=100 mm,初始高度L0=120 mm)經固溶(θs=560 ℃,ts=120 min)水淬后,將管坯放置于模具型腔內,填充顆粒介質于管內;采用通用壓力設備直接給壓頭加載,壓頭下行迫使顆粒介質與管坯共同變形并與模具逐步貼合,從而得到四方形截面管件。直壁圓角未作限制,始終處于自由脹形狀態,隨著壓頭的下移,管內壓力增大,直壁圓角逐步減小。當對角尺寸DW=133.9 mm時,管件直壁圓角處產生破裂,裂紋形式為環向脹裂;當對角尺寸DW≤127.5 mm時,管件脹形完好,如圖7所示。 圖7 AA6061四方截面管顆粒介質脹形工藝試驗裝置Fig.7 Test device of AA6061 square section tube for solid granule medium bulging process 表2 顆粒介質有限元仿真材料性能參數 注:εv為體積應變,pa為平均主應力,σN為正壓力。 圖8 有限元仿真模型Fig.8 Numerical simulation model of finite element 通過仿真得到了不同脹形階段中間截面的輪廓曲線,與實測輪廓基本吻合,見圖9a。分別使用橢圓函數和圓函數擬合管件圓角脹形區輪廓曲線,對比發現,橢圓函數擬合曲線(圖9b)在脹形初始階段擬合效果較好,誤差僅為4%;繼續脹形后,橢圓函數擬合曲線的誤差逐漸增大,在DW=133.9 mm時最大誤差為6%。然而,使用圓函數擬合不同脹形程度的圓角輪廓曲線(圖9c)誤差均為9%左右。由此可知,橢圓函數更適用于自由脹形區的擬合,且在小變形量條件下的擬合精度更高。 (a)中截面輪廓模擬與實測比對 1.ae=42.3 mm,be=28.0 mm,DW=113.3 mm2.ae=40.1 mm,be=28.1 mm,DW=116.9 mm3.ae=37.2 mm,be=26.8 mm,DW=123.5 mm4.ae=32.0 mm,be=23.9 mm,DW=128.2 mm5.ae=28.6 mm,be=23.9 mm,DW=133.9 mm(b)中截面圓角脹形輪廓橢圓函數擬合曲線 工藝試驗獲得了DW=127.5 mm的四方截面管,管件中間截面厚向應變測量值與仿真結果的比對見圖10。結果表明,四方截面管在直壁貼模段與圓角段的過渡區產生的減薄現象與文獻[24-25]中液壓脹形四方型面銅管產生的減薄現象相似,但顆粒介質脹形最大減薄點均產生在直壁圓角中點P21(即最大減薄率為12.5%),且仿真與實測的厚度分布接近。 圖10 AA6061四方截面管厚向應變曲線仿真值與實測值比對Fig.10 Simulation values and measured values of thickness normal strain of AA6061 square section tube 通過數值仿真得到管件中間截面特征點應力值,提取脹形對角線長度DW為116.9~133.9 mm的厚向應力繪制曲線見圖11,應力數據是特征點處厚度方向各層單元輸出數據的平均值。在四方截面管件脹形過程中,中間截面的直壁段(P7)、過渡區(P13)、圓角區(P17)、弧頂(P21)處特征點的厚向應力隨脹形發展呈現不同的變化。管件未貼模時,各處厚向應力均很小,可以視為通常的板殼問題分析,厚向應力忽略不計;管件貼模后,直壁段P7點和過渡區P13點的厚向應力均有顯著的增大,當DW=133.9 mm時,直壁段P7點和過渡區P13點的厚向應力分別達到了-65 MPa和-20 MPa,相比原始管材,脹形后管材的面內應力占比大幅提高。因此,開展與本文研究的四方截面管脹形特征相近似的管狀構件成形性能和力學分析時,應充分考慮厚向應力的影響。 圖11 管件貼模后不同對角尺寸下特征點厚向應力歷程曲線Fig.11 Curves of thickness normal stress of charateristic point under different diagonal dimension after tube fitting 將仿真得到的特征點主應力歷程軌跡繪制到理論3D-FLSD中,見圖12a。由圖12a可以看出,隨著脹形發展弧頂P21點面內主應力的急劇增大,當DW=130.4 mm時P21點主應力值已臨近成形極限曲面,是管件脹形破裂的最危險點;此時,過渡區P13點也接近成形極限,進一步變形時,P13點軸向應力σ1和厚向應力σ3基本不變,徑向應力σ2持續增大,使其軌跡偏離了破裂危險區;直壁段P7點貼模后期,雖然也接近破裂極限,但進一步變形后P7點面內應力增大減緩,僅厚向應力σ3增大,未使其主應力軌跡超出成形極限曲面。由此可知,質點的應力路徑隨著管件脹形發展而不斷變化,管件成形極限與應力路徑密切相關。同樣,可以利用仿真數據繪制不同脹形階段管件從直壁段P7點至弧頂P21點的主應力曲線,見圖12b。由圖12b可以看出,管坯貼模初期(DW=116.9 mm),中間截面各點主應力數值均處于理論3D-FLSD的安全區;當脹形發展至DW=130.4 mm時,各質點均接近破裂區,其中尚未貼模的圓角區是產生破裂失穩的最危險區域。 (a)特征點三維主應力歷程軌跡 (b)不同脹形階段管件中截面主應力曲線圖12 AA6061四方截面管脹形3D-FLSD 成形極限判定Fig.12 3D-FLSD forming limit determination of AA6061 square section tube bulging 工藝試驗結果表明,當DW=127.5 mm時,AA6061四方截面管未發生破裂,脹形系數達到1.23(圖7);當DW=130.4 mm時,管件在過渡區P13點至圓角區P17點之間產生明顯的頸縮現象(圖13a),管材在此區域已進入分散性失穩狀態;當DW=133.8 mm時,管件直壁圓角區產生破裂,裂紋方向垂直于環向應力,為典型的脹斷裂紋(圖13b)。工藝試驗結果得到的失穩現象與通過理論3D-FLSD的判定結果趨于一致。 (a)DW=130.4 mm (b)DW=133.8 mm圖13 不同對角尺寸下AA6061四方截面管工藝試驗失穩狀態Fig.13 Instability states of AA6061 square section tube process test under different diagonal dimension 基于上述成形條件,若采用殼單元分析管件脹形,并通過忽略厚向應力的FLSD判定管材變形失穩,可繪制特征點主應力歷程軌跡,見圖14a。判定結果顯示過渡區P13點在DW=121.3 mm,P17點在DW=116.7 mm時,圓角區P21點在DW=116.3 mm時,管件進入破裂失穩危險區。忽略厚向應力的影響,FLSD(圖14a)和仿真失穩判定云圖(圖14b,即FLDCRT云圖)均提前預判管材的過渡區和圓角區均產生破裂失穩,當圖14b中的FLDCRT值大于1時,則表示材料產生破裂,這與工藝試驗結果相差較大。對于本文研究的四方截面管脹形,采用忽略厚向應力影響的主應力成形極限圖判定失穩過于安全,并不適應成形窗口較小的鋁合金材料。由此可知,在變形較大的鋁合金板殼成形極限分析中,應考慮厚向應力的影響,以充分發揮材料的塑性成形性能。 (a)忽略厚向應力的管件特征點主應力歷程軌跡 (b)忽略厚向應力的管件仿真失穩判定云圖圖14 忽略厚向應力的四方截面管脹形失穩判定Fig.14 Instability deterinination of square section tube bulging with ignoring thickness normal stress (1)AA6061擠壓管材經固溶(θs=560 ℃,ts=120 min)水淬后延伸性能提高了3倍(即Agt=19.8%),與NST管材相比,屈服強度和抗拉強度分別降低了81.4%和40.8%,屈強比減小了60%,斷裂方式由脆性斷裂過渡為韌性斷裂為主,塑性成形性能顯著提高;固溶水淬后再經人工時效(θA=180 ℃,tA=360 min),管材強度可回升至初始值。 (2)數值仿真和工藝試驗結果表明,采用基于擴展的Drucker-Prager線性模型建立的管件脹形有限元模型能夠較為準確地模擬成形過程,管坯變形輪廓和厚度分布與實測規律符合;基于M-K理論建立的考慮厚向應力的3D-FLSD,判定鋁合金管件脹形失穩與工藝試驗結果吻合;FLSD的預測結果偏于安全,對成形窗口較小的鋁合金板殼成形性能分析應充分考慮厚向應力的影響。 (3) 采用“固溶水淬+顆粒介質脹形+人工時效”處理的成形工藝,成功試制了脹形系數為1.23、最大減薄率小于12.5%的AA6061四方截面管件,為高強鋁合金管件的加工提供了新的手段。
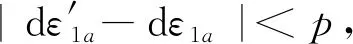
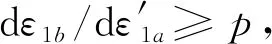
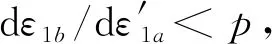
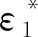
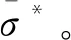
2 AA6061管材3D-FLSD
2.1 材料性能試驗
2.2 斷口觀測



2.3 AA6061管材3D-FLSD分析
3 管件成形仿真與工藝試驗
3.1 管件變形特征分析
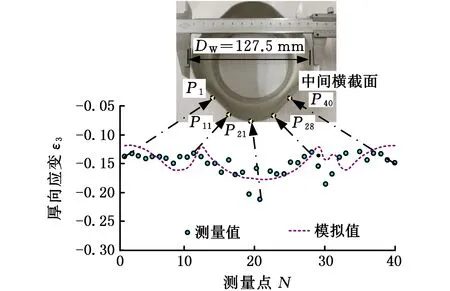
3.2 管件成形性能分析
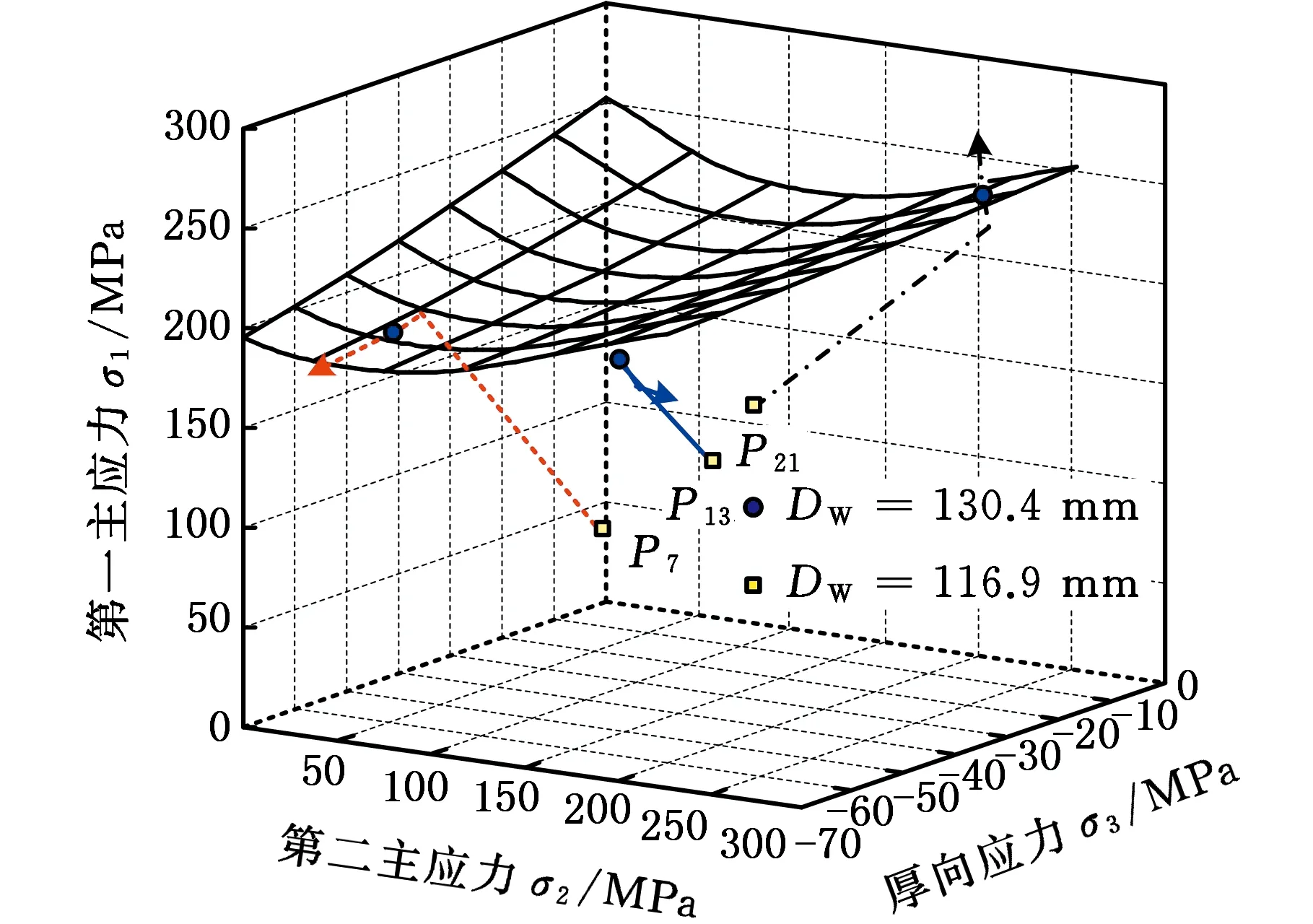
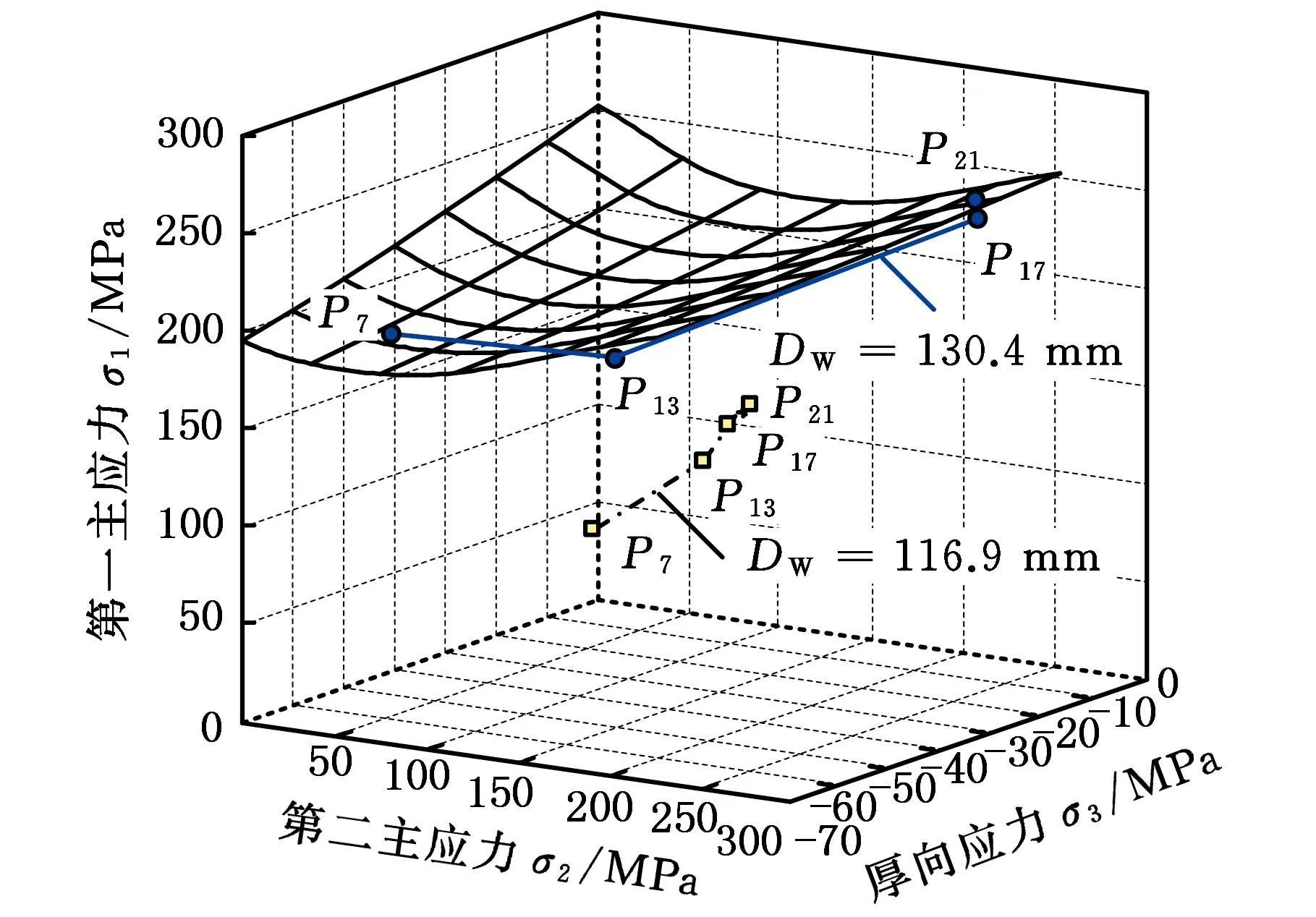
4 結論

