衛星動量輪軸承摩擦力矩性能可靠性動態預測
夏新濤 陳向峰 葉 亮
1.河南科技大學機電工程學院,洛陽,4710032.河南科技大學機械裝備先進制造河南省協同創新中心,洛陽,4710033.西北工業大學機電學院, 西安,710072
0 引言
動量輪軸承組件是滾動軸承的一種,也是衛星姿態控制的關鍵執行部件,其工作動態性能及可靠性直接影響到衛星的控制精度與壽命[1-3]。軸承摩擦力矩是指滾動摩擦、滑動摩擦和潤滑劑摩擦的總和產生的阻滯軸承運轉的阻力矩,是評價軸承運轉靈活性及壽命的重要指標[4];性能可靠度是指在未來時間滾動軸承運行保持最佳性能狀態的程度[5]。
長期以來,軸承性能試驗主要進行疲勞壽命及其可靠度的統計分析,并以威布爾分布為基本假設。CHEN等[6]基于L-P理論和Tallian模型建立了分離軸承新壽命預測模型,其研究結果表明,新型離合器分離軸承壽命預測模型更接近汽車離合器的實際情況;OSWALD等[7]分析了在3種軸承鋼存在高環向應力的情況下,殘余應力對滾動軸承疲勞壽命的影響;朱德馨等[8]從軸承疲勞壽命服從的分布入手,采用貝葉斯多層估計法對無失效試驗數據進行處理,建立了高速列車軸承的可靠性壽命評估模型。但是航空、航天、新能源、新材料等領域的快速發展,對軸承摩擦力矩及其可靠度提出了新要求,使傳統的軸承性能評估理論面臨新挑戰。主要原因有:①受諸多因素的影響,無法推導出摩擦力矩的精確計算公式;②摩擦力矩具有不確定的強烈波動和趨勢變化,屬于概率分布與趨勢規律均未知的問題;③軸承摩擦力矩的研究屬于動力學方程未知的非線性問題,難以找到確定的非線性模型[9-11];④現有的性能可靠性預測方法通常需要事先設定閾值,閾值的設定受主觀因素的影響,缺乏說服力[12-13]。由此可知,如何對滾動軸承摩擦力矩性能可靠性進行動態預測已成為亟待解決的問題。
鑒于以上問題,本文針對衛星動量輪軸承摩擦力矩性能可靠性動態預測展開了研究。將采集到的軸承摩擦力矩原始數據進行分組得到樣本,并選定本征樣本;提出了用灰置信水平求解各樣本變異強度的新方法,該方法既不需要數據概率分布已知,也不需要事先設定閾值;通過自助-最小二乘法和最大熵原理將緊鄰的5個樣本變異強度進行線性擬合,持續更新緊鄰的5個變異強度,不斷舍棄舊數據,引入新數據,從而得到了各樣本摩擦力矩性能可靠度預測值并完成驗證,最終實現了滾動軸承摩擦力矩性能可靠性的動態預測。
1 動態預測模型
1.1 本征樣本
在滾動軸承服役期間,對其摩擦力矩信號進行定期采樣,設采樣周期為t,共采集S個數據。將S個數據均勻分組,設獲得M個樣本,記為X1~XM,樣本含量均為N(即S=MN)。本征樣本是指滾動軸承處于最佳運行狀態時期的樣本,該時期軸承的運轉狀態良好且穩定,幾乎無性能失效的可能性。將本征樣本記為第1個樣本,即
X1=(x1(1),x1(2),…,x1(k),…,x1(N))
(1)
式中,x1(k)為X1的第k個數據;k(k=1,2,…,N)為數據序號;N為樣本含量。
1.2 基于灰置信水平的變異強度和可靠度
設上述任一樣本為Xi(i=1,2,…,M),將樣本X1和Xi中的數據均從小到大排序,通過排序可以得到樣本X1和Xi的數據序列分布特征,進而建立X1與Xi之間屬性的灰關系[14]。
設X1和Xi排序后分別為Y1和Yi,其元素分別為y1(k)和yi(k)。設
(2)
令
(3)
對式(3)進行歸一化處理:
(4)
則有
Zh=(zh(1),zh(2),…,zh(k),…,zh(N))
(5)
zh(k)∈[0,1]zh(1)=0zh(N)=1
式中,Zh為Yh的規范化排序生成序列。
在最少量信息原理下,對于任意的k(k=1,2,…,N),若Zh為規范化排序序列,則參考序列Z0中的元素可以為常數0,即
z0(k)=z1(1)=0
(6)
定義灰關聯度為
(7)
取分辨系數ξ∈[0,1],得到灰關聯系數為
(8)
Δ0h(k)=|zh(k)-z0(k)|
式中,Δ0h(k)為灰差異信息。
定義樣本X1和Xi的灰差為
d1i=|γ01-γ0i|
(9)
則得到樣本X1和Xi的基于灰關聯度的相似系數(即灰相似系數)可表示為
r1i=1-d1i
(10)
定義灰相似矩陣(即灰關系屬性)為
(11)
式中,r11為本征樣本X1與其本身的灰相似系數,則r11=1;rii為樣本Xi與其本身的灰相似系數,則rii=1;r1i、ri1為本征樣本X1與任一樣本Xi的灰相似系數,且有0≤r1i,ri1≤1。
給定樣本X1和Xi,對于ξ∈[0,1],總存在唯一的實數dmax=d1imax,使得d1i≤dmax,則稱dmax為最大灰差,此時對應的ξ稱為基于最大灰差的最優分辨系數。
設基于樣本X1和Xi之間的灰關系屬性權重可表示為
(12)
式中,f1i為屬性權重,f1i∈[0,1];η為參數,η∈[0,1]。
根據白化原理和對稱原理,若沒有理由否認邊界參數θ為真元,則在給定的準則下,默認θ為真元的代表。在給定樣本X1和Xi中,取參數θ∈[0,1]為水平,若存在一個映射f1i≥θ,則表明樣本X1和Xi具有相同的屬性。這里取f1i=θ=0.5,即認為樣本X1和Xi具有相同的屬性。
設η∈[0,0.5],由式(12)可得
dmax=(1-f1i)η
(13)
灰置信水平描述了樣本X1和Xi屬性相同的可信度(概率),其表達式如下:
P1i=1-(1-θ)η=(1-0.5η)×100%
(14)
由于P1i描述的是任一樣本Xi相對本征樣本X1屬性的相似度,故定義Xi相對X1的屬性變異度(即變異強度)為
λi=1-P1i
(15)
變異強度λi的傳統求法是通過計數過程統計得到S個數據中超出設定閾值的數據有v個,則λi=v/S,即數據波動幅值超過設定閾值的概率,但傳統求法的缺點是需要事先設定閾值,若設定的閾值不同,則得到的結果也不同。本文變異強度λi的獲取是基于灰置信水平P1i,不需要事先設定閾值。
任何計數過程均可由Possion過程描述,其表達式如下:
(16)
式中,Q為失效事件發生m次的概率;m(m=0,1,…)為失效事件發生的次數(即滾動軸承性能失效的次數)。
當式(16)中取m=0時,得到滾動軸承未發生性能失效的概率(即表示當前滾動軸承性能可靠度),可表示為
Ri=exp(-λi)
(17)
由于變異強度λi兩種求法的區別僅在于是否需要事先設定閾值,故可將本文中變異強度λi代入式(17)求得任一樣本Xi的性能可靠度Ri。
1.3 動態預測模型的建立
1.3.1基于自助-最小二乘法的變異強度線性擬合
自助-最小二乘法是將自助法和最小二乘法進行融合。運用自助法,將緊鄰5個樣本Xi,Xi+1,Xi+2,Xi+3,Xi+4的5個變異強度λi,λi+1,λi+2,λi+3,λi+4(i=1,2,…,M-4)等概率可放回地隨機抽取q次,得到一個自助樣本Vb,其表達式如下:
Vb=(v1,v2,…,vq)
(18)
式中,Vb為第b個自助樣本;vl為Vb的第l個數據,l=1,2,…,q;q為Vb的樣本含量。
對自助樣本Vb進行均值處理,即
(19)
式中,Vb為自助樣本Vb的樣本均值。
自助樣本Vb重復B次得到VB,VB由樣本均值Vb(b=1,2,…,B)組成,即
VB=(V1,V2,…,VB)
(20)
運用最小二乘法對樣本均值Vb進行線性擬合,其表達式如下:
Vb=abil+cb
(21)
I={i1,i2,…,iq}
式中,I為預測步長;ab、cb為最小二乘解系數。
線性擬合共進行B次,則獲得的最小二乘解系數向量為
a=(a1,a2,…,aB)
(22)
c=(c1,c2,…,cB)
(23)
1.3.2基于最大熵原理的概率密度函數
最大熵原理可對概率分布未知數據作出主觀偏見為最小的最佳估計[15]。以最小二乘解系數ab為例進行其概率密度函數f(ab)的求取,為了敘述方便,將式(22)中離散數據連續化,定義最大熵的表達式為
(24)
式中,f(ab)為系數ab的概率密度函數;S為積分區間。
積分區間S的約束條件為
(25)
式中,β為原點矩階次;mβ為第β階原點矩。
由式(22)可知,B可以是一個很大的數,故得到第β階原點矩:
(26)
通過調整f(ab)可使熵達到最大值,此時可通過Lagrange乘子法進行求解,其表達式如下:
(27)
式中,m為最高原點矩階次;σ0為首個Lagrange乘子;σβ為第β+1個Lagrange乘子。
首個Lagrange乘子σ0應滿足:
(28)
其余Lagrange乘子應滿足:
(29)
同理,可求出系數cb的概率密度函數f(cb)。
1.3.3基于概率密度函數的系數ab和cb估計
根據f(ab),由統計原理可得系數ab的估計真值a0為
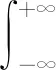
(30)
若δ∈[0,1]存在,使
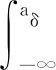
(31)
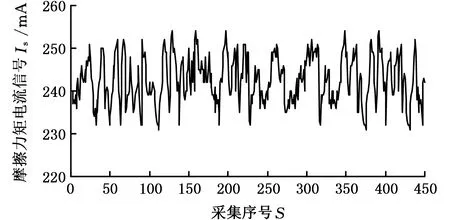
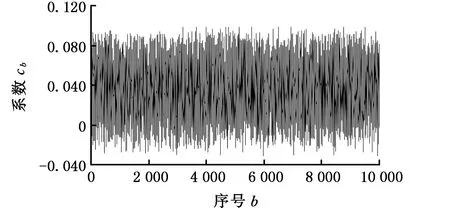
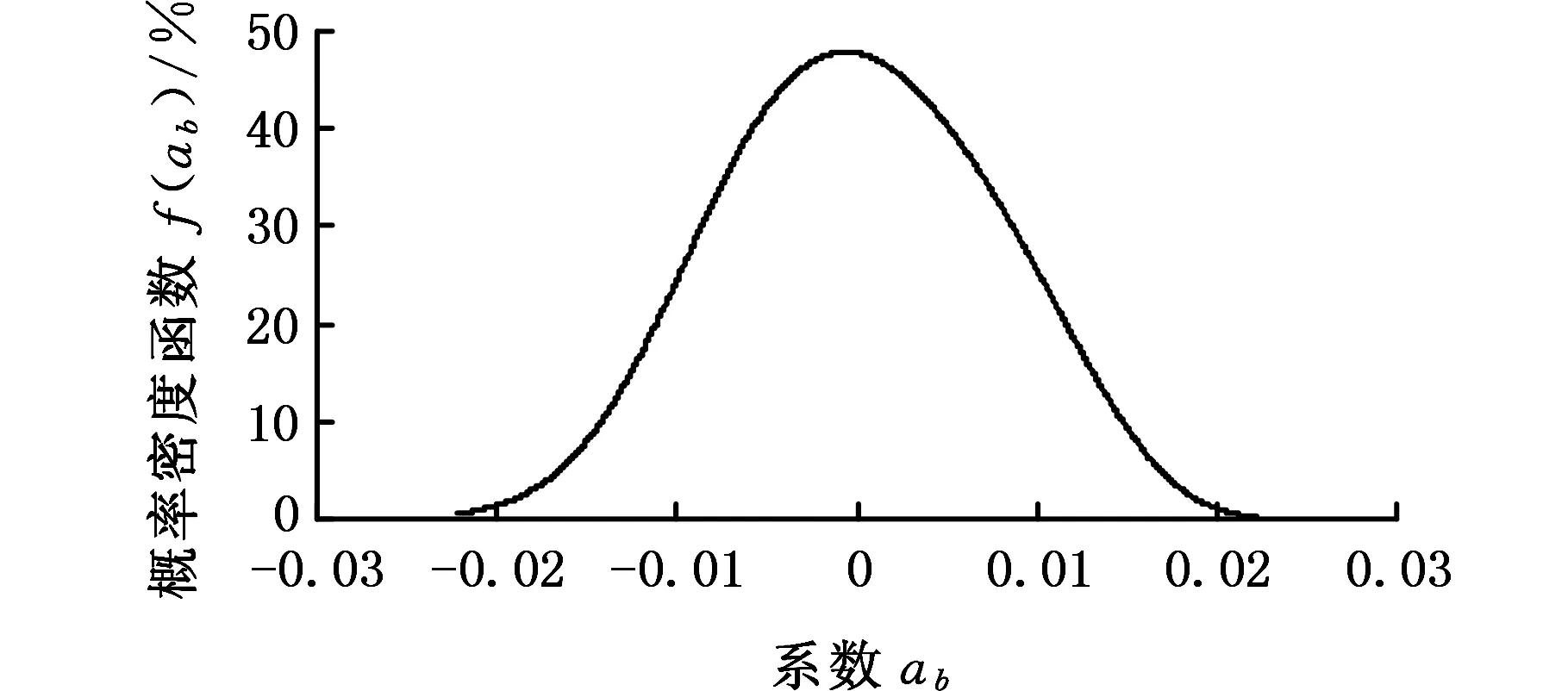
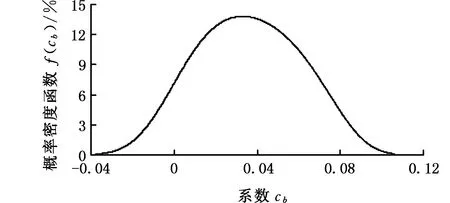
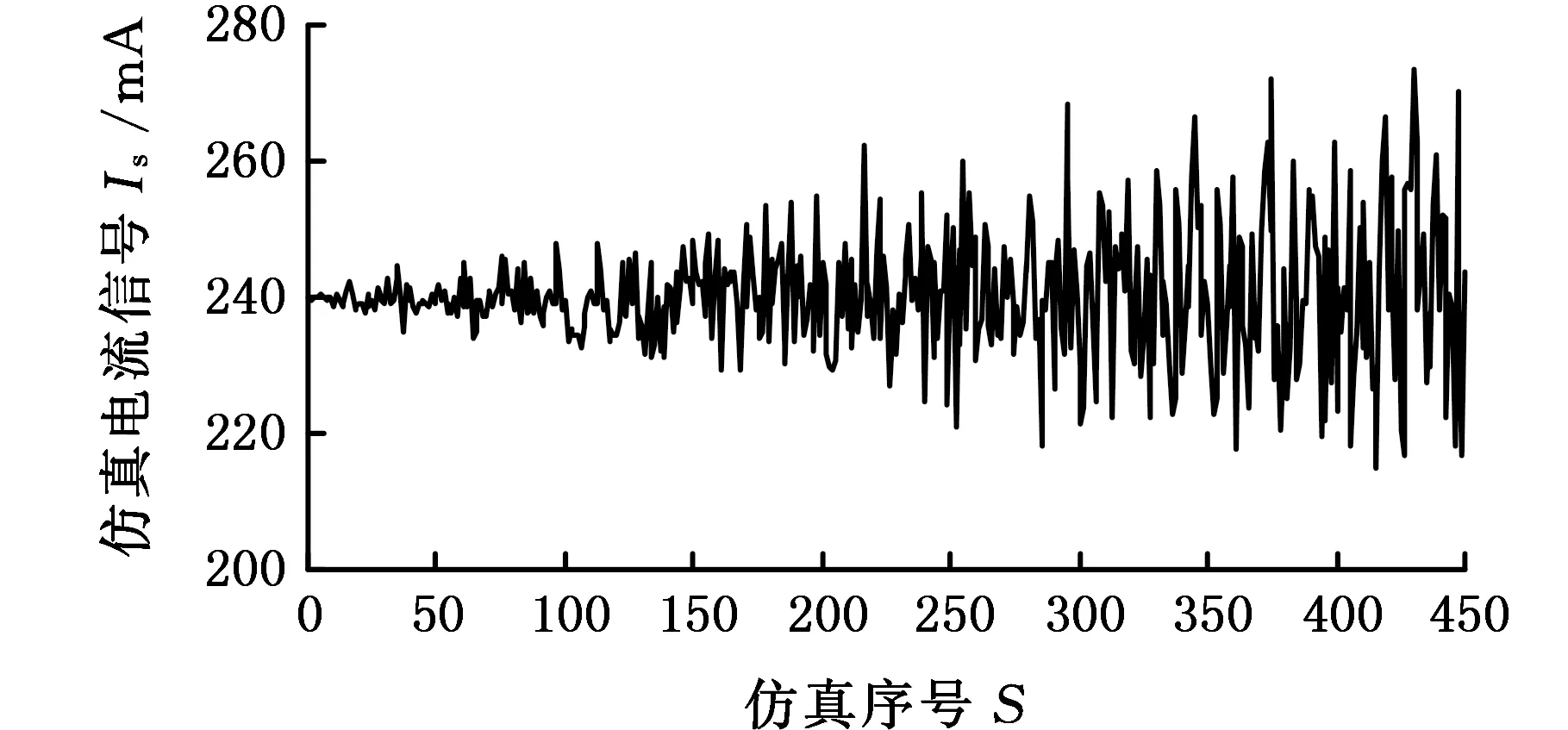
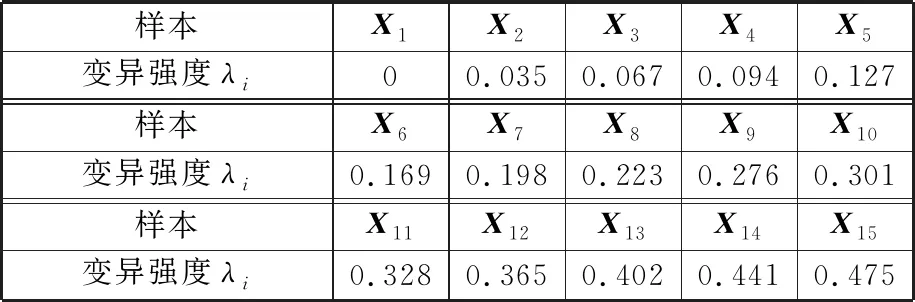
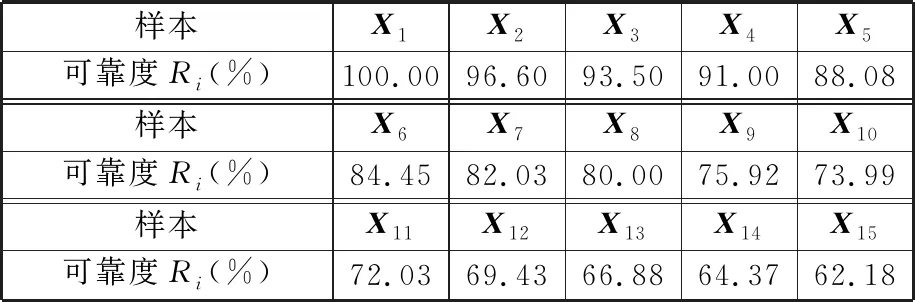
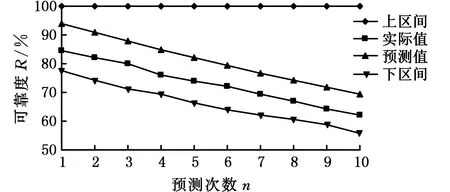
式中,δ為顯著水平(即最小二乘系數ab 為求取最小二乘解系數ab的上下界值,需先求出雙側分位數,則有 P(ab (32) P(ab≥aL)=δ/2 (33) 式中,aU、aL分別為系數ab的上界值和下界值;[aL,aU]為δ水平下的上下區間。 同理,可求得系數cb的估計真值c0與上下區間[cL,cU]。 1.3.4可靠度的動態預測 本研究是一個恒轉速衛星動量輪軸承摩擦力矩穩態電流試驗,在室內溫度20~25 ℃、相對濕度大于55%條件下完成,試驗臺建立在真空罩內的受控清潔和無振動的地基上。衛星動量輪軸承A穩態轉速為3 500 r/min,試驗數據采集周期t=1 d,共采集S=450個(15個月)數據,見圖1。 圖1 衛星動量輪軸承A摩擦力矩穩態電流信號Fig.1 Steady-state current signal of friction torque of satellite momentum wheel bearing A 采集的450個數據均分為15個樣本X1~X15(即M=15),樣本含量均為30(即N=30)。將采集的數據均分為15個時間段,每個時間段為1個月。設樣本X1為本征樣本,得到樣本X1~X15的灰置信水平P1i(i=1,2,…,15),見表1。 表1 樣本X1~X15的灰置信水平 由表1可知,P11=1,表明同一個樣本與其本身屬性完全相同,樣本X1~X15與本征樣本X1的屬性相同的可信度均在0.9以上,表明各時間段內衛星動量輪軸承A摩擦力矩穩態電流信號波動情況較為相似,這與對原始數據直接分析具有一致性。將表1中的P1i(i=1,2,…,15)代入式(15)得到樣本X1~X15相對本征樣本X1的變異強度λi(i=1,2,…,15)的實際值,見表2。 表2 樣本X1~X15的變異強度(實際值) 由表2可知,λ1=0,表明同一個樣本與其本身之間沒有任何變異;λi(i=2,3,…,15)的值均很小,表明試驗過程中的衛星動量輪軸承A摩擦力矩性能未發生明顯變異,軸承一直處于良好的運轉狀態。將表2中的λi(i=1,2,…,15)代入式(17)得到各時間段內衛星動量輪軸承A摩擦力矩性能可靠度Ri(i=1,2,…,15)的實際值,見表3。 表3 衛星動量輪軸承A摩擦力矩性能可靠度(實際值) 由表3可知,各時間段內衛星動量輪軸承A摩擦力矩性能可靠度均大于91%,表明試驗過程中軸承A摩擦力矩性能一直保持較高水平,再次驗證了軸承處于良好的運轉狀態。 以上變異強度λi和性能可靠度Ri都是由原始采集數據運算得到的實際靜態值,為了對衛星動量輪軸承A摩擦力矩性能可靠性進行動態預測,基于自助法將表2中前5個樣本的變異強度(0,0.033,0.067,0.013,0.058)等概率可放回地隨機抽取5次,得到一個自助樣本V1,樣本含量q=5,重復B=10 000次,可得到VB;運用最小二乘法對VB進行線性擬合,可得到最小二乘解系數ab和cb(b=1,2,…,B),分別見圖2和圖3。 圖2 最小二乘解系數abFig.2 The coefficient ab of least square solution 圖3 最小二乘解系數cbFig.3 The coefficient cb of least square solution 為了得到最小二乘解系數ab和cb的估計真值a0、c0及上下區間[aL,aU]、[cL,cU],基于最大熵原理可先求得系數ab和cb的概率密度函數f(ab)和f(cb),分別見圖4和圖5。 圖4 概率密度函數f(ab)Fig.4 The probability density function f(ab) 圖5 概率密度函數f(cb)Fig.5 The probability density function f(cb) 將所求概率密度函數f(ab)和f(cb)代入式(30)~式(33),設定δ=0.1,即在置信度為90%的情況下,求得最小二乘解系數ab和cb的估計真值a0、c0及上下區間[aL,aU]、[cL,cU],見表4。 表4 估計真值a0、c0及上下區間[aL,aU]、[cL,cU] 由圖6可以看出,變異強度的實際值和預測值均在[0,0.1],變化范圍很小,表明各時間段軸承A摩擦力矩性能穩定良好。其中,第1~5次(第6~10個時間段)和第10次(第15個時間段)變異強度預測值和實際值幾乎相等;第6~9次(第11~14個時間段)預測誤差稍微偏大,最大預測誤差出現在第8次(第13個時間段);但所有的預測值和實際值均包絡在上下區間內,預測范圍準確率達100%。 圖7 各時間段摩擦力矩性能可靠度預測結果Fig.7 Prediction results of friction torque performance reliability of each time period 由圖7可以看出,可靠度的實際值和預測值均在91%以上,再次驗證了試驗過程中衛星動量輪軸承A摩擦力矩性能良好,可靠性較高。其中,第1~5次(第6~10個時間段)可靠度的預測值和實際值相差較小,尤其第10次(第15個時間段)可靠度的預測值和實際值幾乎相同;第6~9次(第11~14個時間段)預測誤差稍微偏大,最大預測誤差出現在第8次(第13個時間段);其可靠度預測值上區間的數值達到了100%,且可靠度預測值下區間的數值也在84%以上,且所有可靠度的實際值和預測值均包絡在上下區間內,預測范圍準確率達100%。灰色預測模型GM(1,1)預測結果表明,與實際值相比,其前3次預測結果較為準確,隨著預測次數的增加,預測誤差相對增大,尤其在第5~9次預測,預測誤差較大。這是因為隨著時間的推移,舊信息數據對系統的影響越來越小,新信息數據則反映系統的最新發展狀態,而灰色預測模型GM(1,1)在迭代預測過程中并未及時舍棄舊信息和引入新信息。同時也驗證了所提數學模型用于軸承摩擦力矩性能可靠性動態預測的可行性和正確性。 為了更加直觀地評價所提出動態預測模型的預測效果,計算得到各時間段衛星動量輪軸承A摩擦力矩性能可靠度預測值和實際值的相對誤差,見圖8。 圖8 各時間段可靠度實際值和預測值的相對誤差Fig.8 Relative errors of actual and predicted values of reliability for each time period 由圖8可以看出,各時間段軸承A摩擦力矩性能可靠度實際值與動態預測模型預測值的相對誤差均小于4.1%,其中,第1~5次(第6~10個時間段)、第7次(第12個時間段)和第10次(第15個時間段)的可靠度預測誤差均小于3%,最小的預測誤差出現在第10次(第15個時間段),僅為0.1%,動態預測模型的預測值和實際值幾乎完全相等;而灰色預測模型GM(1,1)預測相對誤差幾乎均大于動態預測模型預測誤差,且后期預測誤差相對增大。上述研究結果再次驗證了所提出動態預測模型的正確性。 隨著軸承轉速的變化,摩擦力矩電流信號將出現隨機波動,且隨著轉速的增大,這種波動將越來越劇烈。為了模擬出這種電流信號變化趨勢,本文采用蒙特卡羅法仿真出15個正態分布樣本X1~X15(樣本基本值均為240 mA,樣本標準差從1逐漸增加到15),樣本含量均為30,共450個仿真數據,見圖9。 圖9 仿真電流信號Fig.9 Simulated current signal 由圖9可以看出,仿真電流信號隨機波動越來越強烈,可模擬出軸承摩擦力矩電流信號隨軸承轉速變化的越來越不穩定的變化趨勢。軸承摩擦力矩性能可靠度預測過程如下。 以X1為本征樣本,由式(2)~式(17)計算得到X1~X15各時間段軸承摩擦力矩性能變異強度和可靠度,分別見表6和表7。 表6 樣本X1~X15的變異強度(預測值) 由表7可知,X1~X15各時間段軸承摩擦力矩性能可靠度逐漸降低,這與原始數據波動越來越劇烈相一致。 將表6中的λ1~λ5進行迭代預測,可得到軸承摩擦力矩性能可靠度預測結果及預測值與實際值的相對誤差,分別見圖10和圖11。 表7 軸承摩擦力矩性能可靠度(預測值) 圖10 仿真摩擦力矩性能可靠度預測Fig.10 Reliability prediction of simulated friction torque 圖11 可靠度實際值和預測值的相對誤差Fig.11 Relative errors of actual and predicted values of reliability 由圖10可以看出,軸承摩擦力矩性能可靠度實際值和預測值保持幾乎相同的減小趨勢,表明原始仿真電流信號波動越來越強烈,軸承摩擦力矩性能可靠度越來越低;可靠度預測值上區間的數值達到了100%,可靠度預測值下區間的數值持續減小至60%左右,且所有可靠度實際值和預測值均包絡在上下區間內,預測范圍準確度100%。由圖11可以看出,可靠度預測值與實際值的相對誤差均在9.4%以內,較大誤差出現在第1次和第4次預測,分別為9.34%和9.07%;第6~10次預測結果的預測誤差穩定在7.2%~7.4%。 (1)將灰置信水平、自助-最小二乘法和最大熵原理融合,并應用到衛星動量輪軸承摩擦力矩性能可靠性動態預測中;提出了用灰置信水平求解變異強度的新思路,彌補了變異強度傳統求法中需要事先設定閾值的缺點。 (2)所提出動態預測模型是對原始試驗數據本身計算得到的客觀規律,對數據概率分布特征沒有任何要求,彌補了傳統統計學中需要事先已知數據概率分布的不足。 (3)試驗分析結果表明:所提出動態預測模型可實現各時間段衛星動量輪軸承A摩擦力矩性能可靠度預測結果的驗證;恒轉速條件下可靠度預測誤差均小于4.1%,變轉速條件下可靠度預測誤差也不超過9.4%。 (4)可通過改變自變量I的取值,更改預測步長,為實現超精密滾動軸承在線監控及故障診斷提供參考。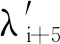
2 試驗分析
2.1 恒轉速衛星動量輪軸承摩擦力矩穩態電流試驗
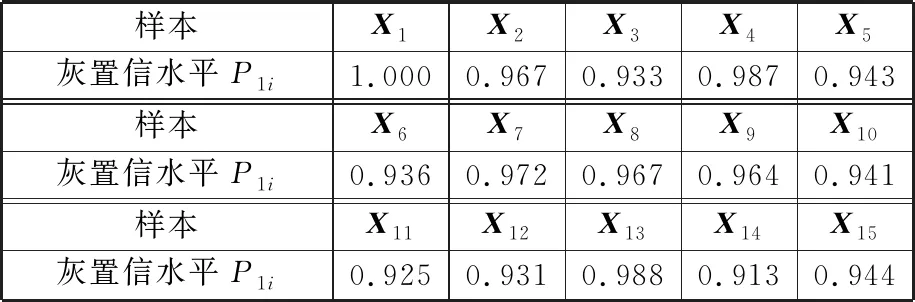
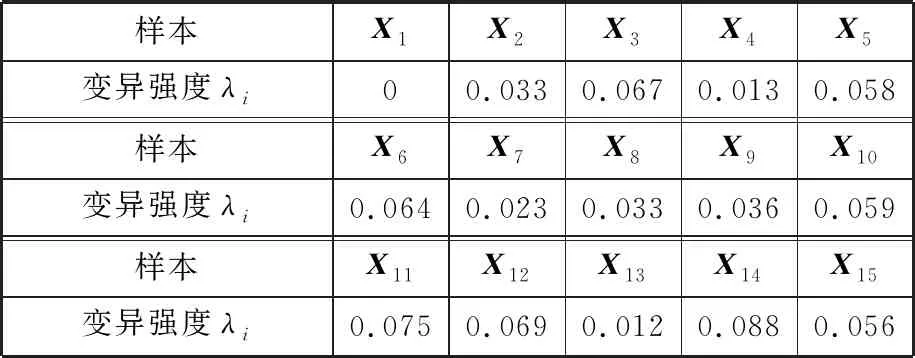
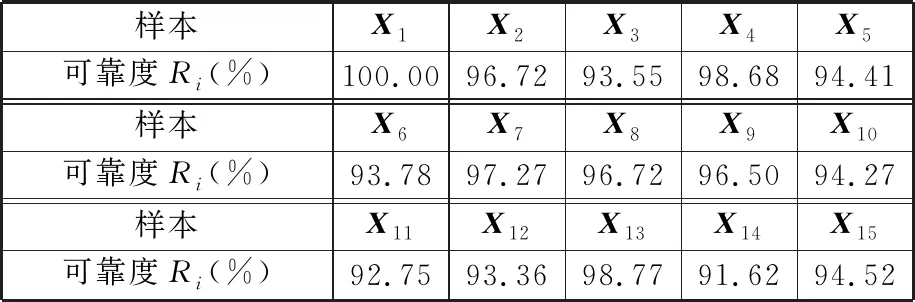
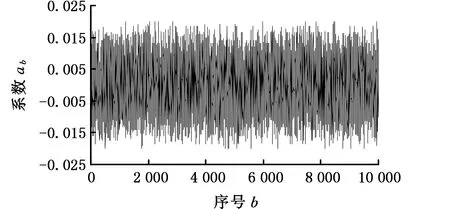

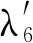
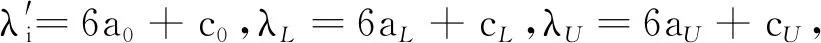
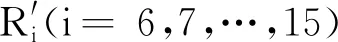

2.2 變轉速衛星動量輪軸承摩擦力矩仿真分析

3 結論

