基于模糊熵和模糊夏普比率的多階段投資組合模型及實證

王中興，盧余剛

(廣西大學數學與信息科學學院, 廣西南寧530004)

0 引言

平衡投資的收益和風險，確定各種資產的投資比例是投資組合研究的重要組成部分。MARKOWITZ[1]在1952年使用收益的方差來度量風險，建立了期望收益最大、風險最小的均值—方差投資組合模型。在此之后，許多學者開始關注投資組合的收益度量問題。例如SWALM[2]利用半方差衡量風險；KONNO[3]用絕對方差來度量風險等。以上學者從風險度量的角度提出了許多經典的投資組合模型，如均值—半方差投資組合選擇模型，均值—絕對方差投資組合選擇模型等。眾所周知，高收益總是伴隨著高風險，那么風險和收益如何抉擇？1966年SHARPE[4]提出了Sharpe比率，Sharpe比率的定義為超出無風險收益的收益率與標準差的比值，衡量每個單位風險所獲得的超額收益。隨后，許多學者基于Sharpe比率提出了一系列的改進，例如SORTINO等[5]利用下側風險替換Sharpe比率中的標準差。VINOD等[6]使用原始樣本生成再生樣本，進而提出“雙重Sharpe比率”。ZAKAMOULINE等[7]提出了調整的Sharpe比率等。由于資產收益率存在模糊不確定性，2015年NGUYEN等[8]提出了模糊Sharpe比率，用模糊收益率代替傳統Sharpe比率中清晰收益率。

在投資的過程中，由于市場影響因素比較復雜，資產的風險和收益率具有很強的不確定性。因此人們基于ZADEH[9]提出的模糊集概念以及LIU[10]提出的不確定理論來研究投資組合問題。例如ZHANG等[11]把投資組合收益看作模糊隨機變量，建立了基于可能性均值方差的投資組合模型；王竟竟等[12]提出了具有交易量和交易成本約束的多期模糊投資組合模型。為了描述模糊變量的隨機不確定性，LI等[13]定義了一種新的模糊熵，在此基礎上BHATTACHARYYA等[14]等提出了一個新的投資組合模型，該模型使得均值和偏度最大化，方差和交叉熵最小化。DENG等[15]建立了帶有交易成本的模糊投資組合模型，并分析了算法的靈敏度。另外由于投資者投資行為的長期性，研究多階段投資組合問題也具有重要意義。MERTON[16]研究了連續時間下的多階段投資組合問題，SADJADI[17]在假設借貸利率不相等的情況下，研究了模糊多階段投資組合問題。

本文利用模糊熵度量投資收益的不確定性，模糊夏普比率衡量投資效率，以資產組合收益和投資效率最大、投資風險最小為決策目標，構建多階段的多目標投資決策模型，并采用理想點法將模型轉化為單目標優化模型并利用遺傳算法進行求解。

1 可信性均值及模糊夏普比率

1.1 可信性均值和模糊熵相關概念

為了將模糊變量清晰化，文獻[10]在模糊數的基礎上提出了可能性測度和必要性測度，進而給出了模糊變量的可信性均值，可信性方差和模糊熵等概念。

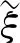
(1)

(2)

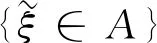
(3)

即:

(4)

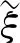
(5)

(6)

(7)

對于風險資產投資組合問題，文獻[18]分別定義資產組合的可信性收益，可信性方差和模糊熵如下：

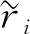
(8)

(9)

(10)

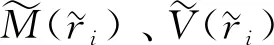
1.2 模糊夏普比率

(11)

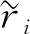
(12)

其中Rb表示無風險資產收益率。

2 模糊多階段投資組合模型

2.1 模型建立

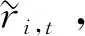
(13)

第t期投資者的財富值Wt可以表示為：

(14)

其中t=1,2,…,T。通過對式(14)進行迭代，第h期(h=1,2,…,T)投資者擁有的總財富Wh可表示為：

(15)

(16)

(17)

投資目標為最終財富價值最大化，并且使整個投資過程的累積夏普比率最大化，模糊熵最小，則建立基于模糊熵和模糊夏普比的多階段投資組合模型如下:

(18)

模型(18)第一個約束要求各資產投資比例之和為1。第二約束代表投資比例上下界限制。可以看出，該模型的經濟意義是指在上述兩個約束條件下，投資者通過分配投資比例來最小化投資組合的風險，最大化投資效率，實現財富最大化。

2.2 模型求解

由于模型(18)為多目標投資組合模型，其最優解難以求出，通常做法是將多目標優化轉換為單目標優化。本文利用理想點法進行轉換，理想點法的基本思想是對于多目標規劃問題：

(19)

先分別求出各個分目標函數φi(x)和φj(x)的最優值φi,max(x),(i=1,2,…,n)和φj,min(x),(j=1,2,…,m)，將這些由最優值構成的點稱為理想點，然后根據實際點與理想點之間的距離構造評價函數和單目標優化問題：

(20)

即在多目標規劃的可行域內，盡可能的“逼近”理想點。

利用上述理想點法將多目標規劃化模型(18)轉化為動態單目標規劃模型：

(21)

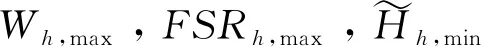
3 實證研究

從上海證券交易所A股抽取了10支股票，這10支股票屬于不同行業。數據選取的時間區間為2015年至2018年(數據收集自同花順軟件)，計算此區間的日收盤價，以一年為一個計算周期，使用文獻[20]提出的頻數統計法對數據進行處理，得到每支股票的三角模糊收益率，具體數據如表1。

表1 股票模糊收益率Tab.1 Stock fuzzy return rate

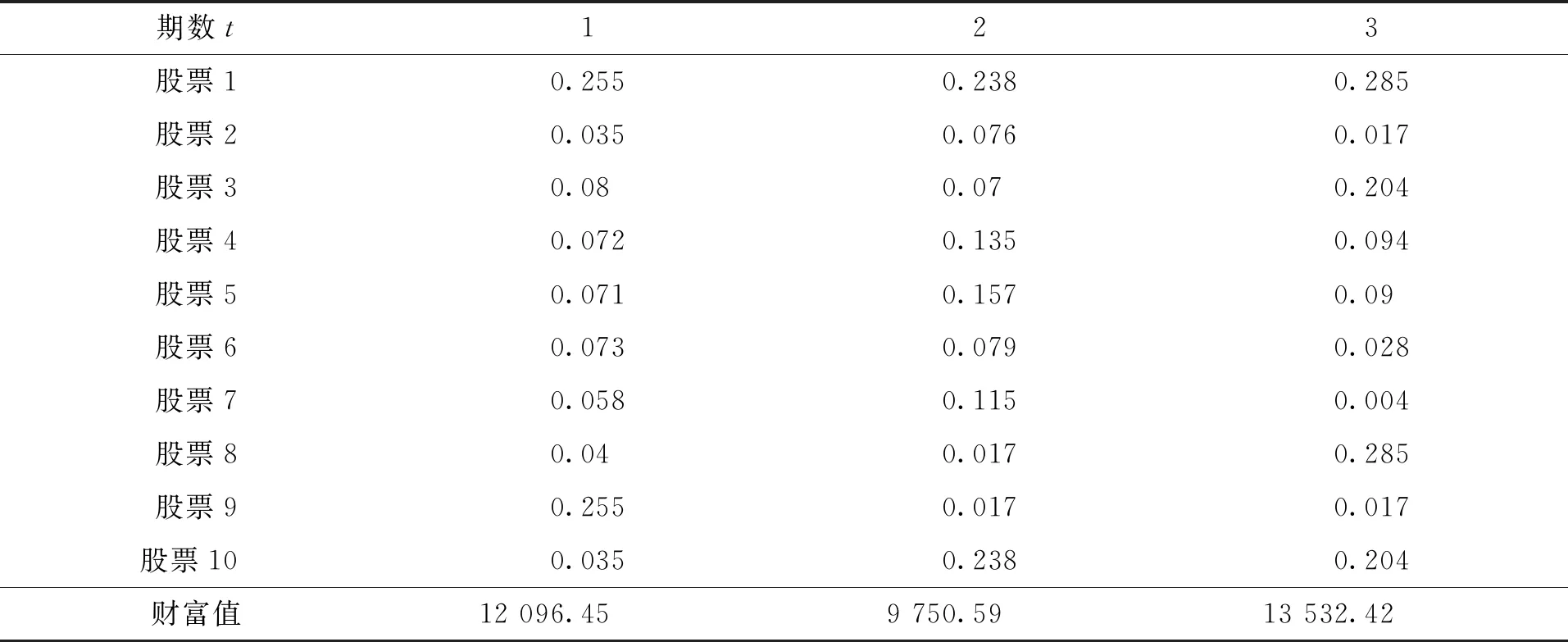
表2 股票最優投資比例及各期財富Tab.2 Optimal investment ratio of stocks and periodic wealth

由表2可以看出，基于模糊熵和模糊夏普比率的多階段投資組合的模型最優解分布性較好，在第一期投資結束后投資和擁有12 096.45元，在第二期投資結束后，受市場大盤整體低迷的影響，其資產變為9 750.59元。在第三期投資結束后投資者扭虧為盈，總資產變為13 532.42元。從上述實證數據說明了該模型在中國證券市場下的實用性和有效性。

投資組合問題一直是許多學者研究的重點問題。本文在已有文獻的基礎上，利用模糊熵度量投資風險，模糊夏普比率衡量投資績效，構建了多階段投資組合模型。實證數據(表3～表5)表明基于該模型的投資決策可行、有效，投資者可以在實際投資中參考。

表3 t=1時股票具體數據 Tab.3 t=1 Stock specific data

表4 t=2時股票具體數據Tab.4 t=2 Stock specific data

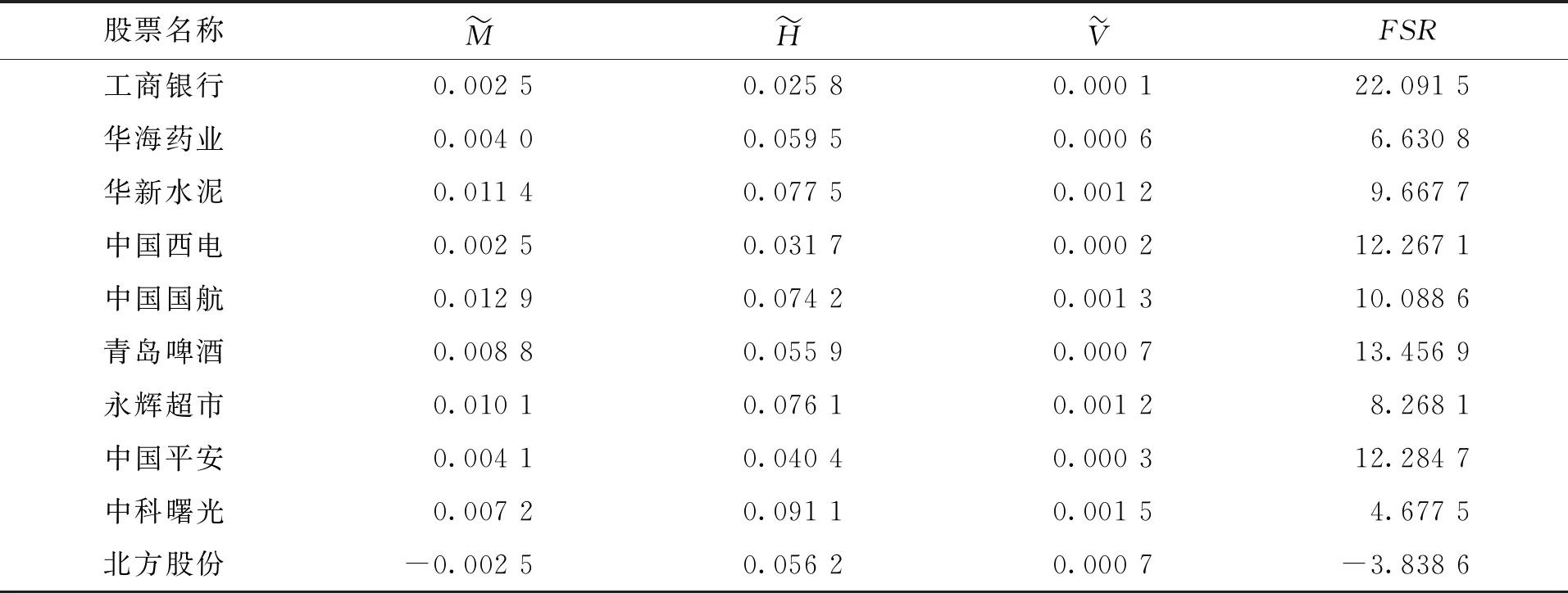
表5 t=3時股票具體數據Tab.5 t=3 Stock specific data