帶落角約束的非奇異快速終端二階滑模制導律*

尤 浩,趙久奮,李 朋,宋林浩

(1 火箭軍工程大學, 西安 710025;2 中電科儀器儀表有限公司技術支持部, 山東青島 266000)

0 引言

隨著現代戰爭的快速發展,導彈攻擊地面機動目標時,需要導彈以較小脫靶量擊中目標同時導彈以指定角度攻擊目標[1-2],以提高毀傷效能。

滑模變結構控制理論具有對參數選取的不敏感性和對外部擾動的強魯棒性[3],因此廣泛應用在制導律設計中。文獻[4]針對線性滑模面收斂速度較慢的問題,在滑模面中引入線性函數以提高收斂速度,但造成了收斂過程中的奇異問題。文獻[5]基于非奇異終端滑模設計制導律的過程中避免了奇異問題的出現,但制導律只適用于攻擊靜止或弱機動目標。文獻[6]提出了一種適用于攻擊機動目標的滑模制導律,并設計了非線性觀測器對目標機動信息進行估計,但需要目標機動上界,而目標機動上界一般很難獲得。文獻[7]提出了一種有限時間收斂的積分滑模面,結合快速冪次趨近律,設計了適用于攻擊機動目標制導律,并對未知機動目標干擾上界進行自適應估計。但上述文獻研究的都是一階滑模制導律,而二階滑模制導律具有抑制抖振能力強、魯棒性強的優點[8],因此基于二階滑模控制理論設計帶落角約束的有限時間收斂制導律具有很強的工程應用價值。

為提高滑模面的收斂速度,并抑制抖振現象,文中基于非奇異快速終端滑模和二階滑模控制理論設計了帶落角約束的有限時間滑模制導律,設計制導律的過程中避免了奇異問題的出現。并設計了非齊次干擾觀測器對系統中未知目標機動信息帶來的擾動進行估計,無需目標先驗信息,有利于工程應用。

1 系統模型建立

1.1 彈目相對運動模型

考慮導彈在二維平面中攻擊地面機動目標問題,導彈和目標的相對運動關系如圖1所示。

圖1中,Oxy是地面慣性坐標系,M和T分別表示導彈和目標。q為彈目視線角,規定由彈目視線r順時針旋轉到水平基準線時為正,反之為負;θm表示導彈M的彈道傾角,θt表示目標T在俯仰方向上的航向角,規定速度位于水平基準線上方時為正,反之為負;vm、am、vt和at分別表示導彈和目標的速度和法向過載。根據圖1中彈目相對運動關系,得到導彈末制導數學模型為:

(1)

(2)

(3)

(4)

將導彈速度vm在地面慣性坐標系Oxy兩個坐標軸上分解,得到導彈的運動方程為:

(5)

分別對式(1)和式(2)求導,并將式(3)和式(4)代入,得到

(6)

(7)

式中:ur、uq表示導彈M在視線方向上和視線法向上的加速度分量;wr、wq表示目標T在視線方向上和視線法向上的加速度分量。在末制導段,彈目相對速度在視線方向上的分量遠小于0,并且彈目相對加速度在視線方向上的分量很小,在只考慮脫靶量和落角約束的情況下,導彈和目標加速度在視線方向上的分量ur和wr造成的影響可以忽略不計,因此將ur和wr設定為0,僅利用式(7)設計視線法向上的制導律uq。uq和wq對應的表達式為

uq=amcos(q-θm)

(8)

wq=atcos(q-θt)

(9)

1.2 帶落角約束問題和設計目標

假設導彈擊中目標時刻,導彈攻角可以近似為0,則導彈攻擊落角可以近似為導彈和目標的彈道傾角之差。設期望落角為σd,則

σd=θmf-θtf

(10)

式中:θmf和θtf為導彈擊中目標時刻導彈彈道傾角和目標航向角。根據零化視線角速率思想,導彈擊中目標時刻有

-vtsin(qf-θtf)=vmsin(qf-θmf)

(11)

式中:qf為導彈擊中目標時刻的視線角。設

(12)

求解式(11)并將式(10)和式(12)代入,得到

(13)

若導彈攻擊固定目標,θtf=0,導彈期望落角為攻擊時間導彈彈道傾角;若導彈攻擊非機動目標,θtf可通過θt的初值得到;若導彈攻擊機動目標,θtf可通過彈上跟蹤濾波器得到,因此可以假設θtf為已知。由式(13)可知,對于每一個指定的期望攻擊角度σd,存在一個與之一一對應的終端視線角qf,因此導彈攻擊落角約束問題可以轉化為視線角的跟蹤問題。

(14)

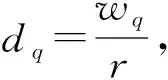
2 制導律設計

針對系統狀態方程式(14),選取非奇異快速終端滑模面如下：

s=x1+k1sig(x1)a1+k2sig(x2)a2

(15)

對滑模面式(15)求導,并將式(14)代入,得

(16)

為使系統狀態有限時間內收斂到滑模面,并沿著滑模面運動,在有限時間內收斂到系統期望狀態,針對式(16),設計二階滑模制導律如下:

式中：α和β均為大于0的常數,y>2,z1為下文將要設計的非齊次干擾觀測器對系統式(16)中擾動dq的估計值。

對于式(16)中由目標機動信息帶來的擾動dq,設計如下非齊次干擾觀測器對dq進行估計。

(18)

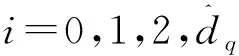
證明: 假設非齊次干擾觀測器式(18)在時間tr收斂到系統干擾的真實值dq,則當t≥tr時,將制導律式(17)代入到式(16),化簡后得

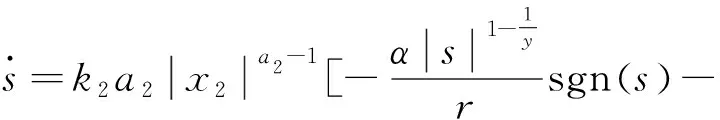
(19)

為方便分析,引入以下狀態變量:

(20)

(21)

對式(21)求導可得

(22)

容易發現,矩陣A為Hurwitz矩陣,因此對任意矩陣Q=QT,存在對應矩陣P=PT>0,滿足如下代數黎卡提方程:

ATP+PA=-Q

(23)

對系統式(22)選取如下Lyapunov函數:

V1=ρTPρ

(24)

對式(24)求導后將式(22)代入,得到

(25)

(26)

式中:

(27)

(28)

當|x2|=0,且tr

(29)

當t≥ts,即系統狀態收斂到滑模面s=0時,則式(15)變為:

x1+k1sig(x1)a1+k2sig(x2)a2=0

(30)

對系統式(30),選取Lyapunov函數如下：

(31)

對式(31)求導,并將式(30)代入,得到

(32)

將式(31)代入到式(32),化簡后得到

(33)

式(33)具有同式(26)結構,由文獻[10]中引理1可得,x1在有限時間內收斂到0,并且由式(30)可得,當x1=0時,x2也在有限時間內收斂到0。證畢。

3 仿真分析

為驗證文中提出的制導律式(17)的有效性,設置導彈在不同落角約束下攻擊機動目標。仿真參數設置為:導彈和目標的初始位置分別為(5 000 m,5 000 m),(10 000 m,0 m);導彈的速度vm=300 m/s,初始彈道傾角為θm0=-20°;設置目標做常值機動,目標初始速度vt=30 m/s,加速度at=0.4gm/s2,初始俯仰方向航向角為θt0=30°。制導律式(17)中的仿真參數選取如下:a1=3,a2=1.1,k1=k2=1,α=500,β=600,γ=2.1。非奇異干擾觀測器中的仿真參數設置為λo=1.1,λ1=1.5,λ2=2,μo=3,μ1=6,μ2=8,L=0.1。

導彈的期望落角分別為σd=-30°,-60°,-90°,制導盲區設置為20 m,即導彈進入制導盲區后按進入制導盲區瞬時的加速度飛行。導彈法向過載限制為30g,g=9.81 m/s2,仿真步長設置為1 ms,得到仿真結果如圖2所示。

從圖2可以看出,在確定目標的機動方式下,文中提出的制導律式(17)能夠擊中目標且滿足落角約束。法向加速度在制導末期,收斂到0附近的小鄰域內,并且收斂過程中光滑無抖振現象出現,有利于導彈自動駕駛儀的控制。視線角速率在制導末期均收斂至0,保證了導彈能夠擊中目標。滑模面在有限時間內收斂到0,收斂過程中光滑無抖振現象出現。驗證了提出的制導律對抖振現象良好的抑制作用。上述的仿真和分析表明,文中提出的制導律針對強機動目標能夠滿足落角約束的同時以較小脫靶量擊中目標,加速度保持在合理的范圍內并且無抖振現象出現,驗證了制導律的強魯棒性和工程適用性。

為驗證提出制導律的優越性,將非奇異快速終端二階滑模制導律記為SO-NFTSMG,與標準非奇異滑模制導律[11](記為NTSMG)進行仿真對比,NTSMG的表達式為：

(34)

式中：K為符號函數增益,根據目標機動上界選取,本文仿真中選取K=100,式中其余參數同制導律式(17)參數選取。得到仿真結果如表1和圖3所示。

圖2 3枚導彈攻擊機動目標仿真結果

從表1可以看出,兩種制導律作用下的導彈落角誤差差別不大,但SO-NFTSMG作用下的導彈脫靶量較NTSMG作用下的脫靶量減小約0.18 m,說明制導律SO-NFTSMG有效提高了制導精度。從圖3(c)、

圖3(d)和圖3(f)中看出,SO-NFTSMG作用下的視線角、視線角速率和滑模面在較短的時間內收斂到期望值,驗證了制導律SO-NFTSMG快速收斂的優點。從表1中看出,NTSMG作用下的導彈飛行時間較SO-NFTSMG減少約0.6 s,這對于飛行時間較短的導彈末制導段而言,在一定程度上增大了突防概率。但從圖3(d)、圖3(e)中看出,NTSMG作用下的視線角速率和法向加速度在收斂過程中出現了不期望的高頻抖振,不利于導彈自動駕駛儀的控制。而SO-NFTSMG作用下的視線角速率和法向加速度在收斂過程中沒有出現高頻抖振,驗證了SO-NFTSMG抑制抖振能力強的優點。綜合而言,文中提出制導律制導精度高,收斂速度快,對抖振現象的抑制能力強,驗證了文中提出制導律的優越性能。

4 結論

基于非奇異快速終端滑模和二階滑模控制理論設計了帶落角約束有限時間滑模制導律。證明了制導律的穩定性和有限時間收斂特性,設計非齊次干擾觀測器對目標機動信息進行估計,無需目標先驗信息。通過與不同制導律的仿真對比,結果表明:設計的制導律對脫靶量和落角的控制能力強,能控制導彈以較小的脫靶量和落角誤差擊中機動目標,并且具有制導精度高,收斂速度快,對抖振現象的抑制能力強的優點,具有一定的實際應用價值。