基于空間笛卡爾坐標系轉換的三軸一體光纖陀螺標定數學建模*

趙桂玲,姜雨含,李 松

(遼寧工程技術大學測繪與地理科學學院, 遼寧阜新 123000)

0 引言

光纖陀螺(fiber optic gyroscope,FOG)以其啟動時間短、動態范圍大、抗沖擊、壽命長、測量精度高等優點在捷聯慣性導航系統(strap-down inertial navigation system,SINS)中得到快速發展和廣泛應用[1-2]。作為捷聯慣性導航系統的核心部件,光纖陀螺標定精度直接影響慣性導航系統的工作精度[3-4]。光纖陀螺標定精度取決于三軸一體光纖陀螺標定數學模型精度以及基于數學模型的標定路徑設計與參數估計方法。國內外對光纖陀螺標定技術的研究主要集中在:利用慣性測試轉臺提供的速率和位置進行分立式標定[5]；利用Kalman濾波技術進行標定參數估計的系統級標定方法[6-9]；利用GPS、磁傳感器、光電成像系統等提供的外界輔助信息進行在線標定[10-12]。無論哪類載體、哪種方法進行光纖陀螺標定,都是在假設光纖陀螺標定模型固定已知的前提下進行理論推導和實驗,鮮有對標定模型本身精確性、可靠性及適用性的分析,部分探討與研究也只是分析具體參數對固定模型的影響[13],缺乏對模型嚴格準確的推導,而標定模型在一定程度上決定了標定方法的選擇和標定參數誤差分配,并對系統性能評估具有重要的指導意義。

如果光纖陀螺標定模型過于簡化,參數估計簡單,工程易于實現,但不能滿足系統精度的要求；如果將所有認知的模型參數都考慮在內,又會給實驗室標定或系統在線標定帶來困難,況且有些系數在激勵不夠的情況可以忽略。針對以上關鍵工程應用問題,從光纖陀螺標定模型的物理意義出發,以光纖陀螺坐標系相對載體坐標系之間的安裝誤差角為切入點,提出基于空間笛卡爾坐標系轉換矩陣的三軸一體光纖陀螺標定數學建模方法,建立3種工程常用的光纖陀螺標定線性數學模型,并給出模型中各個參數的物理意義和模型的適用條件。最后通過仿真和一套光纖陀螺捷聯慣性導航系統標定與導航試驗結果對3種模型進行比較和分析。

1 數學建模

文中從三軸一體光纖陀螺的工程安裝結構出發,兼顧慣性導航系統補償精度和標定試驗難度,對三軸一體光纖陀螺進行數學建模。

1.1 單軸光纖陀螺數學模型

由于光纖陀螺具有標度因數線性度好、動態和靜態誤差小等優點[14],一般情況下單軸光纖陀螺標定常采用線性輸入輸出模型。光纖陀螺沒有與g和g2相關的誤差項,且忽略隨機誤差的影響,單軸光纖陀螺脈沖輸出與角速率之間的轉換模型為:

Ng=Kgωg+D0

(1)

式中:Ng為光纖陀螺脈沖輸出;ωg為光纖陀螺輸入角速率;Kg為光纖陀螺標度因數;D0為光纖陀螺零偏。

1.2 空間笛卡爾坐標系變換

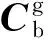
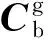
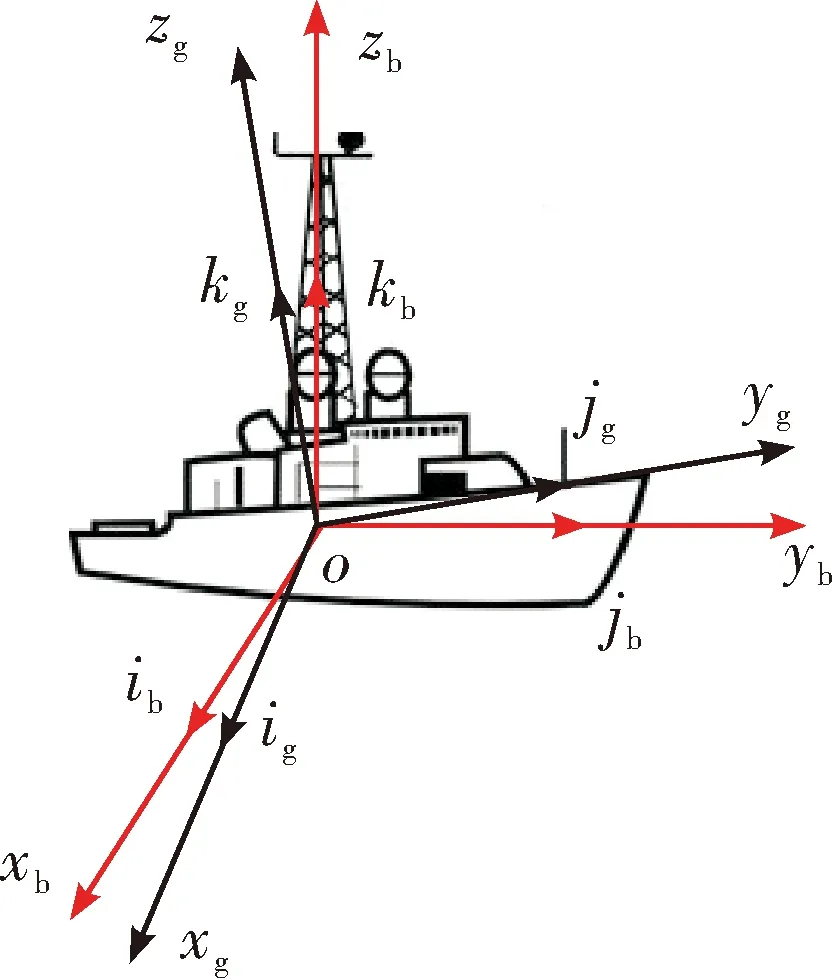
圖1 兩坐標系安裝示意圖

根據空間笛卡爾坐標系基變換公式,可得b系到g系的基變換公式:

(2)

b系到g系的坐標變換矩陣:

(3)

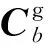
2)式(3)是在3個光纖陀螺任意安裝下求得的坐標系變換矩陣,一般情況下,g系3個軸與b系對應軸在空間笛卡坐標系內成小角度安裝,此時:

(4)

式(3)可簡化為:

(5)

3)式(5)是式(3)下的一種特例與簡化,更進一步,假設g系3個軸與b系對應軸在空間笛卡坐標系內不但成小角度安裝,且g系3個軸正交安裝,即g系構成空間笛卡爾直角坐標系,則:

cosθmgnb=-cosθngmb;m≠n;m,n=i,j,k

(6)

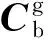
(7)

此時,b系到g系的坐標系變換,也可以通過圖2的3次旋轉實現。

圖2 b系到g系的坐標系旋轉

將3次旋轉表述成3個獨立的方向余弦陣,b系到g系的變換用3個獨立的方向余弦陣乘積表示。

(8)

當旋轉角ψ、θ、φ為小角度時,對式(8)進行化簡,并忽略二階以上小量,可得:

(9)

對標定而言,式(7)和式(9)具有相同的表現形式,但兩矩陣元素Cij(i≠j)表達的物理意義卻不同,對于小角度轉動,

(10)

1.3 三軸一體光纖陀螺數學模型

三軸一體光纖陀螺是一種將慣性導航所需3個正交方向的陀螺設計成一體化的光纖陀螺,根據單軸光纖陀螺數字量與角速率之間的轉換模型,將三軸一體光纖陀螺模型寫成矢量形式:

Ng=Kgwg+D0

(11)

式中:

(12)

式中：wg是角速率矢量在陀螺坐標系g系下的投影,而慣性導航解算需要的是角速率矢量在載體坐標系b系下的投影wb,由于安裝誤差的存在,wb與wg之間存在如下關系:

(13)

將式(13)代入式(11),可得三軸一體光纖陀螺靜態輸入輸出標定數學模型為:

(14)

(15)

(16)

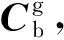
2 六位置光纖陀螺標定

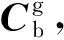
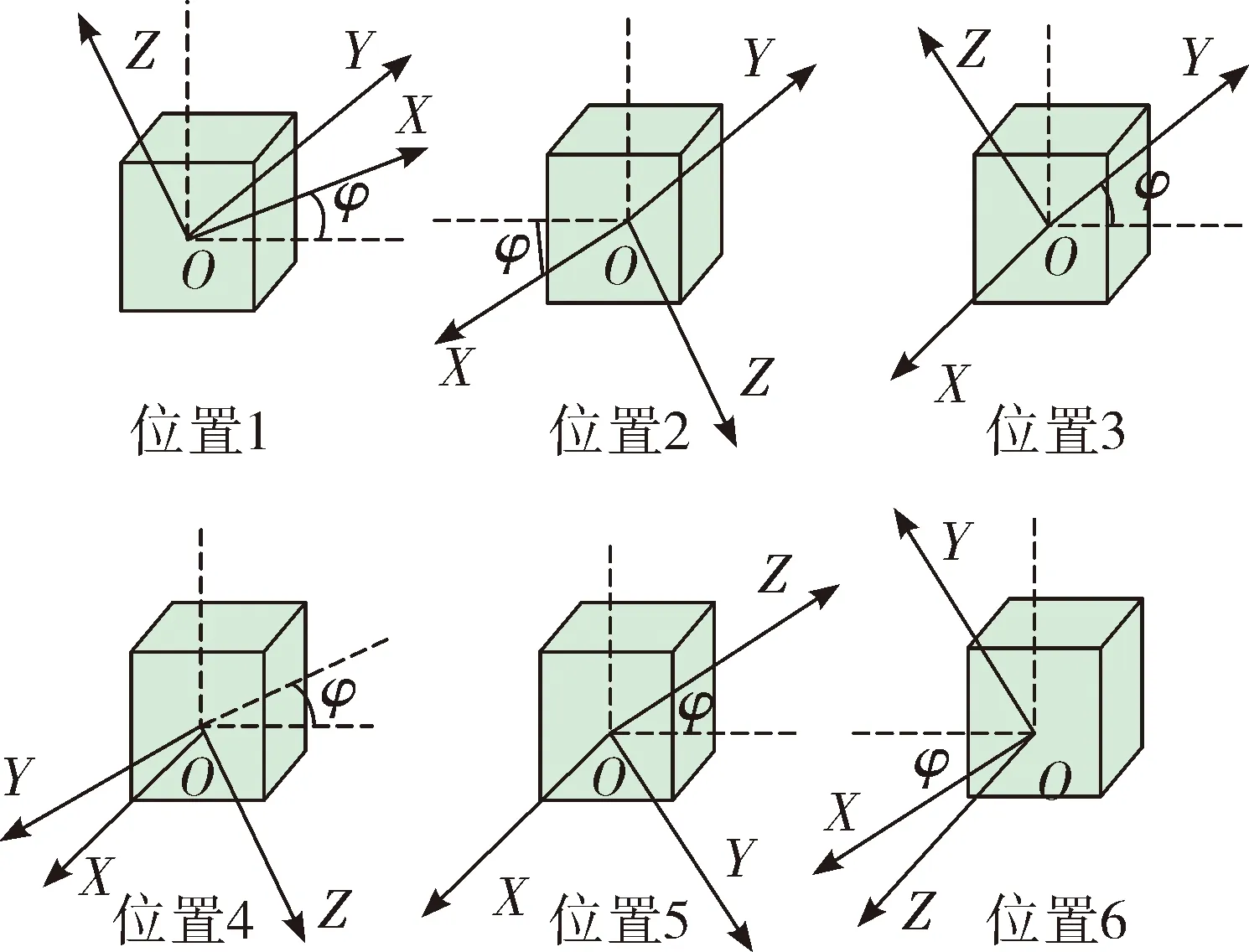
圖3 光纖陀螺標定路徑設計

(17)

根據6個位置的光纖陀螺脈沖輸出,可以計算出三軸一體光纖陀螺標定數學模型參數:

(18)

(19)

(20)

將式(19)～式(20)計算出的標定模型參數代入式(16),則可以根據任意的光纖陀螺脈沖輸出計算光纖陀螺的輸入角速率wb。

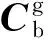
(21)

(22)

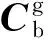
(23)

3 仿真及實驗分析

3.1 計算機仿真

采用六位置標定方法對三軸一體光纖陀螺進行標定,忽略轉臺定位誤差、加速度計誤差、初始對準誤差等對系統的影響,在靜止條件下分析光纖陀螺簡化模型標定數學模型對系統的影響。仿真條件如下:

簡化的光纖陀螺標定數學模型對姿態、速度、位置的影響如圖4～圖9所示:

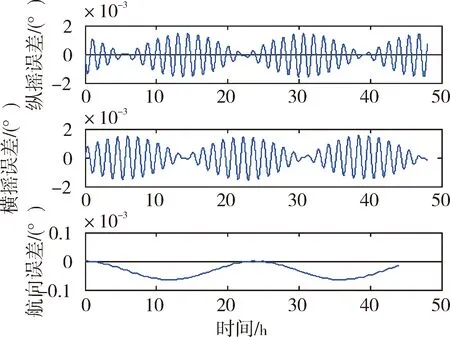
圖4 3個安裝誤差角簡化模型對姿態的影響

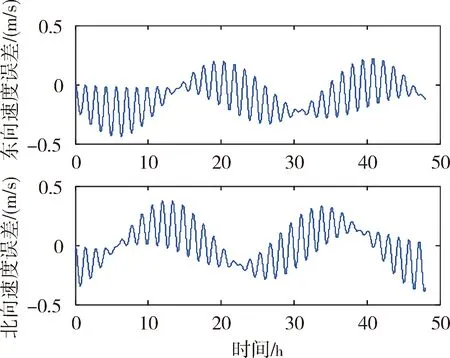
圖5 3個安裝誤差角簡化模型對速度的影響

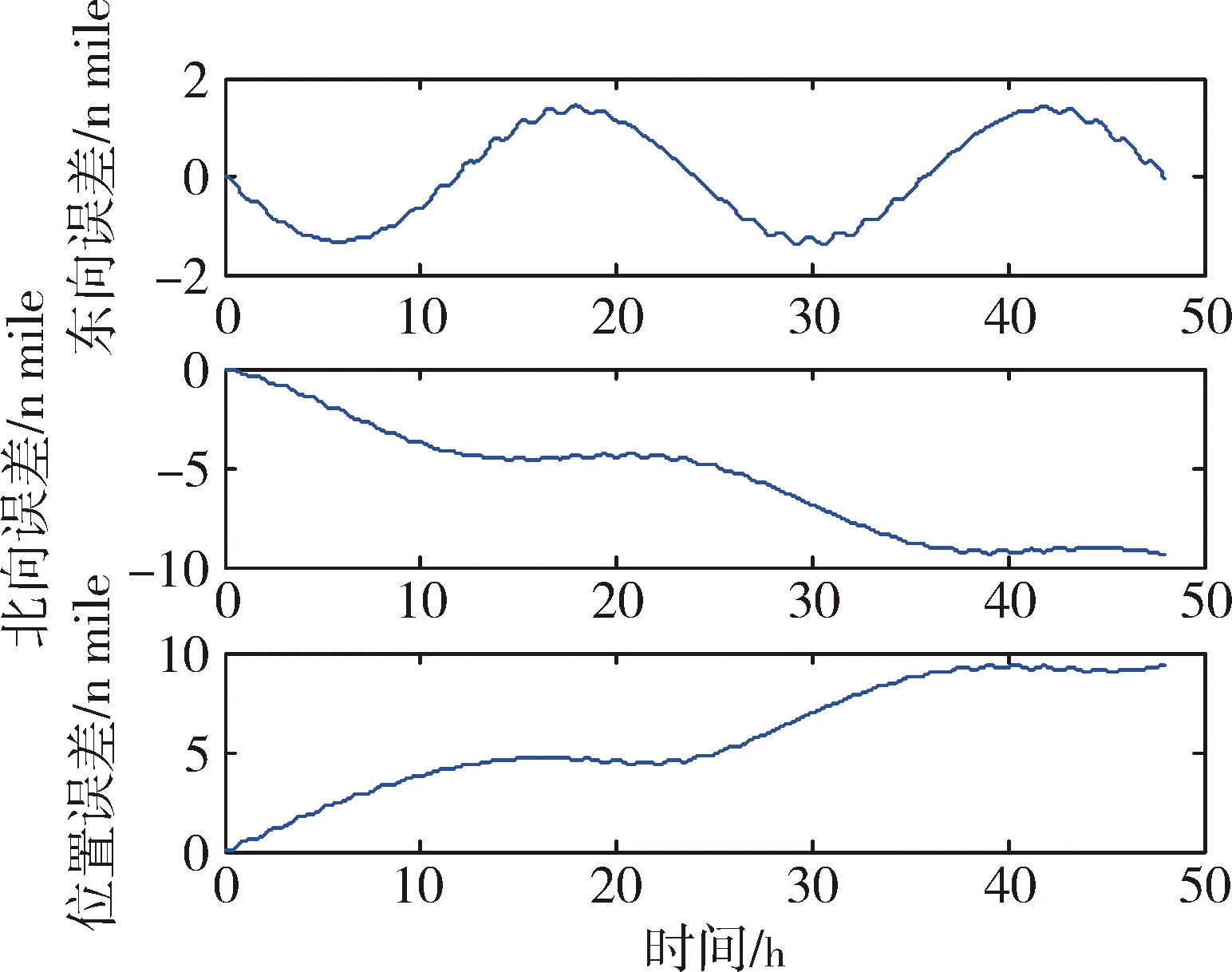
圖6 3個安裝誤差角簡化模型對位置的影響

從仿真圖可以看出:在0.1o隨機安裝誤差條件下,簡化的三軸一體光纖陀螺標定數學模型引起捷聯慣性導航系統速度誤差、位置誤差和姿態誤差。簡化為3個安裝誤差角形式的標定數學模型引起的系統導航誤差大于6個安裝誤差角形式的標定數學模型引起的系統導航誤差。兩種簡化形式的標定數學模型均引起隨時間增長的位置誤差。

3.2 轉臺實驗

將光纖陀螺捷聯慣性導航系統置于三軸慣性測試轉臺,轉臺角位置精度3 ″。控制轉臺按照圖3設計的光纖陀螺標定路徑進行旋轉,每個位置停留2 min,采集光纖陀螺輸出,按照式(17)～式(23)分別對3種數學模型進行參數分解,并將計算結果代入捷聯慣性導航系統進行導航解算,導航結果如圖10所示。

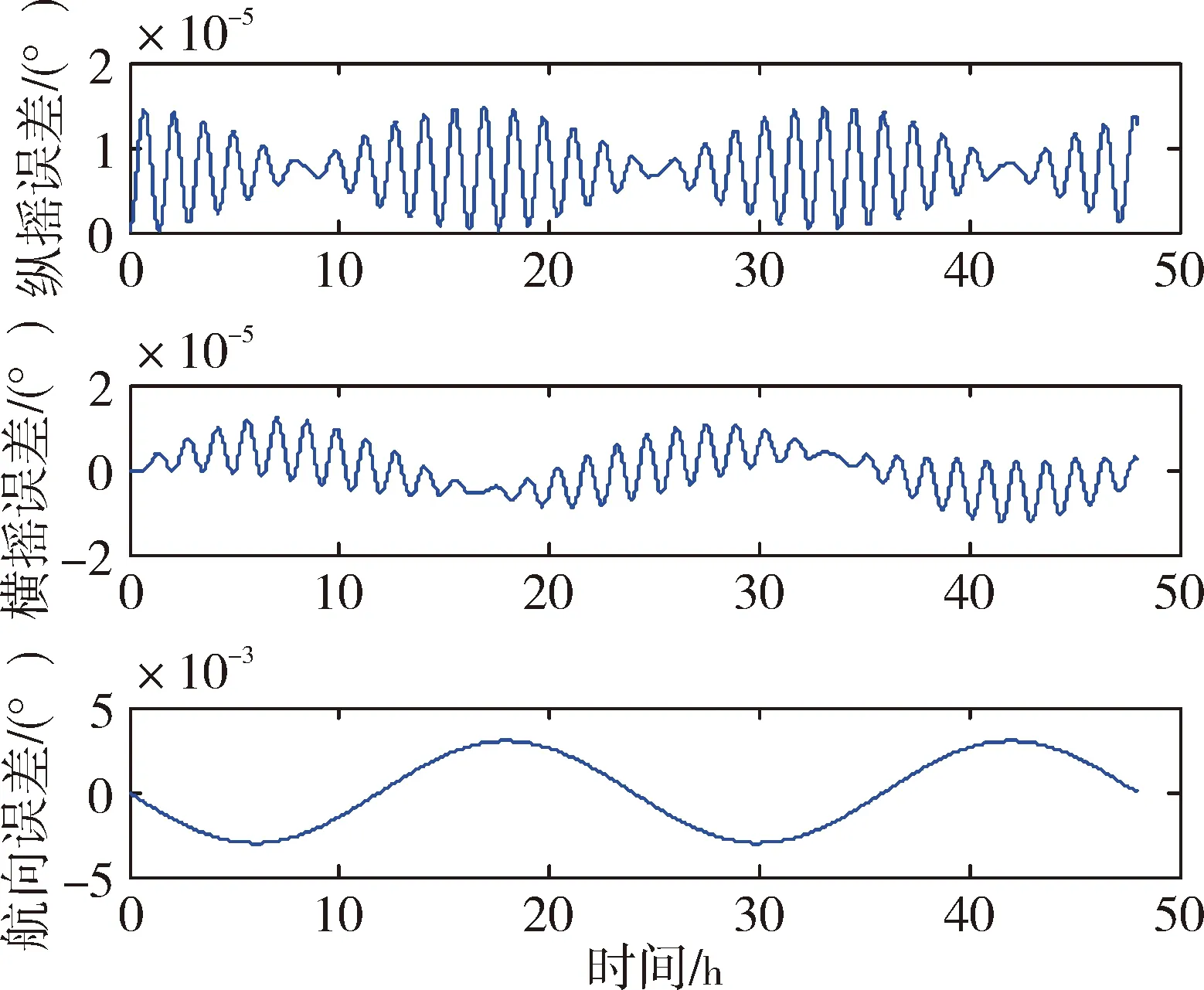
圖7 6個安裝誤差角簡化模型對姿態的影響

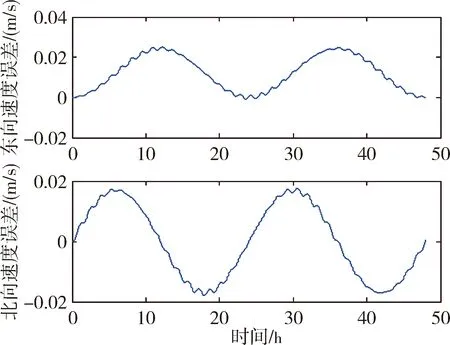
圖8 6個安裝誤差角簡化模型對速度的影響

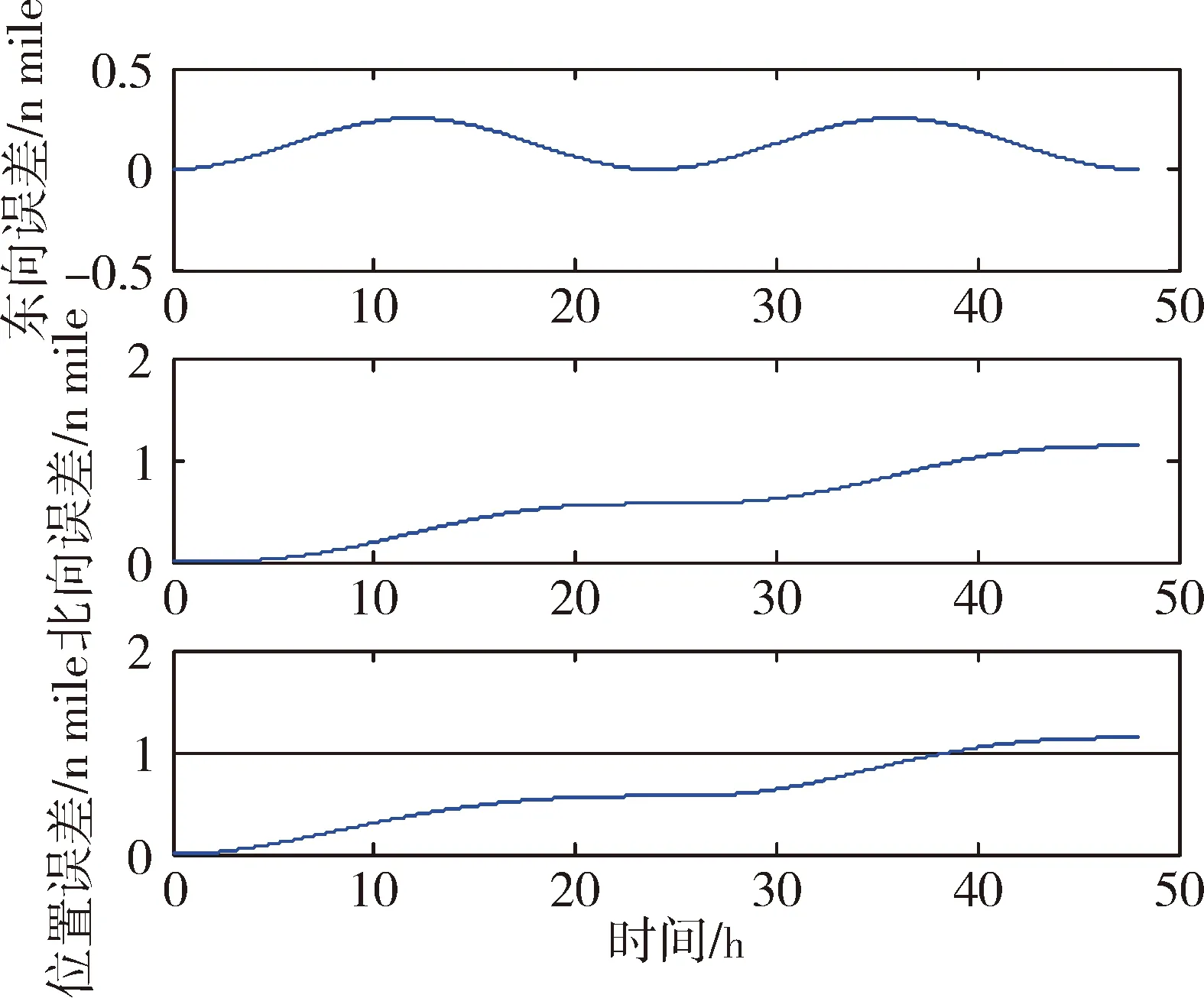
圖9 6個安裝誤差角簡化模型對位置的影響

三軸一體光纖陀螺標定數學模型采用的安裝誤差角為9個、6個和3個時,靜態導航定位誤差分別為4.15 nmile/40 h、6.02 n mile/40 h合20.21 n mile/40 h。3個安裝誤差角形式的光纖陀螺標定數學模型引起的定位誤差遠大于6個安裝誤差角形式的標定模型和9個安裝誤差角形式的標定模型引起的定位結果。實驗誤差大于仿真結果,這是因為在標定實驗和導航實驗中,不可避免的會存在加速度計誤差、轉臺定位誤差、初始對準誤差等,這些都對導航結果產生一定的影響。

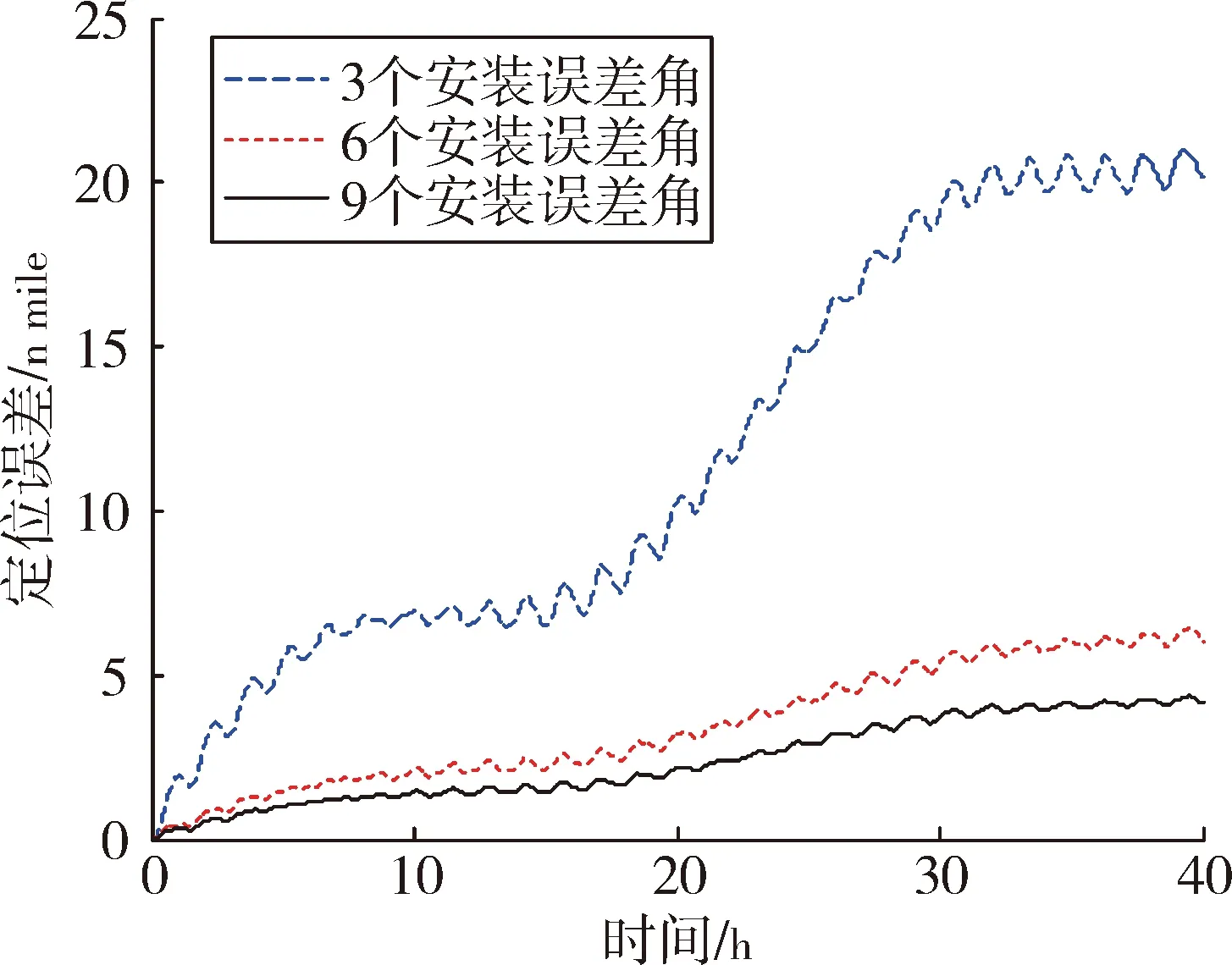
圖10 導航定位誤差

4 結論

文中提出一種基于空間笛卡爾坐標系轉換矩陣的三軸一體光纖陀螺標定數學建模方法,建立了3種光纖陀螺標定數學模型,給出模型中各個參數的物理意義,并通過六位置標定方法對3種數學模型中的參數進行標定。計算機仿真及實驗結果表明:簡化的光纖陀螺標定數學模型對系統速度、位置、和姿態都有影響,影響的大小與光纖陀螺標定誤差模型參數有關,模型參數越多,模型越精確,引起的導航誤差越小,越能滿足精度要求。