考慮邊界約束條件的懸索橋有限元模型修正研究

鄒向農，龍俊賢，陽德高，胡朋，韓艷

?

考慮邊界約束條件的懸索橋有限元模型修正研究

鄒向農1，龍俊賢1，陽德高2，胡朋2，韓艷2

(1. 中鐵武漢勘察設計研究院有限公司，湖北 武漢 430074；2. 長沙理工大學 土木工程學院，湖南 長沙 410114)

針對以往模型修正過程中常忽略邊界約束條件影響的問題，為考慮大橋初始有限元模型中邊界約束條件與實際情況的差別，以某塔梁分離的懸索橋為工程背景，以現場動載測試結果為基本依據，采用Combine14單元模擬該懸索橋加勁梁的縱向約束作用，運用響應面方法并結合大橋特點選取一系列算法組合考慮了邊界約束條件對懸索橋初始有限元模型的影響，并對其進行修正。研究結果表明：考慮了邊界約束條件的修正結果與懸索橋實測值更為接近，且各修正參數的修正量均在合理范圍內，驗證了上述考慮邊界約束條件的方法在有限元模型修正中的有效性。修正后的模型可以作為該懸索橋的基準有限元模型，并可為大橋的進一步響應分析提供基礎。

有限元模型修正；邊界約束條件；響應面法；動載試驗

隨著計算機技術的高速發展，有限元方法在橋梁結構中已獲得廣泛的應用，建立一個準確的有限元模型對于結構的靜動力響應分析、損傷識別、健康監測等起著至關重要的作用。初始有限元模型通常依據現有的設計或施工圖紙建立，由于施工、材料隱藏缺陷、建模過程中不同程度的簡化和假定等影響，使得有限元模型與實際結構會存在一定程度的偏差。為修正這種偏差，研究中常利用靜動力試驗結果，對初始有限元模型的剛度、質量、邊界約束及幾何參數等進行修正，在保證模態參數自身精度的前提下，使修正后有限元模型的計算結果更接近于試驗值[1?2]，修正后的模型更能如實地反映實際結構的力學行為。傳統的橋梁有限元模型修正通過修改系統的質量矩陣和剛度矩陣，使修正后模型的計算值與實測值相同。但該方法有2大不足，一是基于靈敏度分析的有限元模型修正需要進行迭代計算，每計算一次就需要調用有限元模型一次，模型修正所需的時間長、計算量大；另一個是復雜結構進行模型修正時修正的參數較多，需要多次有限元計算，不易實現。相比之下，基于響應面方法的有限元模型修正更具有優勢，首先在參數的整個設計空間范圍內利用試驗設計和回歸技術，以顯式的響應面函數模型代替復雜的結構特征響應量與設計參數間復雜的隱式關系，從而得到簡化的結構模型；在此基礎上，進行迭代計算，這不僅可避免每次迭代都需要調用有限元模型進行計算，而且基于方差分析的參數篩選是在整個設計空間范圍內，改善了傳統局部靈敏度分析篩選參數的弊端，大大提高了模型的修正效率，因而使其在橋梁結構有限元模型修正中得到了廣泛的應用[3]。基于響應面方法，任偉新等[3]利用某6跨連續梁橋環境振動試驗結果對大橋初始有限元模型進行修正，取得了比較顯著的效果，并驗證了運用響應面方法進行有限元模型修正的有效性和高效性。魏錦輝等[4]利用某橋的現場靜動力響應測試結果，考慮結構材料特性與幾何參數等因素，利用響應面技術對該橋的初始有限元模型進行修正，并建立了該橋的基準有限元模型。周林仁等[5]考慮材料特性與質量配比等因素，通過建立徑向基函數響應面模型，以斜拉橋自振頻率和靜態索力構造目標函數，對該大橋的實驗室物理模型進行修正并取得了比較良好的效果。李剛[6]采用基于響應面的模型修正方法，分別對工字鋼梁、足尺軌道梁和三跨連續梁的有限元模型進行修正，并對比靜力法、動力法和聯合法的修正效果，同時探討了采用動態權重法構造目標函數的作用和適用條件。王蕾等[7]利用某大橋模態頻率實測值，以對應的橋面單元、中墩、邊墩的彈性模量、密度等設計參數為修正參數，構造徑向基神經響應面模型對該大橋的初始有限元模型進行修正，取得了理想的效果。以上研究均采用響應面方法對橋梁有限元模型進行修正，且取得了比較理想的效果，但需要指出的是，以上橋梁邊界約束條件均較明確，研究中也未針對橋梁的邊界約束條件進行修正。本文擬研究的某大橋為塔梁完全分離的大跨度懸索橋結構，這與以往同類型橋梁的邊界條件約束不同。該大橋自建成通車以來，由于施工工藝、材料隱藏缺陷、長時間運營及縱向約束模擬不確定性等因素，通過設計圖紙建立的初始有限元模型會與實際結構有所差別，對其進行初始有限元模型修正、建立更符合實際情況的有限元模型有一定的必要性。研究中采用Combine14單元模擬懸索橋加勁梁的縱向約束作用，以Combine14單元剛度值等為修正參數，利用大橋現場動力測試數據結果，采用響應面方法對初始有限元模型進行修正，為大橋進一步的分析提供有限元模型基礎。

1 基于響應面方法的橋梁有限元模型修正算法選取

基于響應面方法的橋梁有限元模型修正，是數理統計與模型修正技術的集合。其基本思想是在實驗設計的有限次有限元計算的基礎上，擬合得到結構特征響應量與各設計參數間的顯式函數關系，并用此響應面模型代替結構初始有限元模型進行迭代計算，實現結構有限元模型的參數修正[8-10]。鑒于響應面方法的高效優勢，本文采用響應面方法來進行考慮邊界約束的有限元模型修正。

樣本的選取關系到響應面模型的精度和計算效率，如何用最少的樣本點獲得理想的響應面模型至關重要。進行響應面常用的設計方法有中心復合設計、全因子設計、正交設計、均勻設計和D-最優設計。由于D-最優實驗設計方法在進行實驗設計時所需計算次數較少，且用于大規模模型的響應面建模精度最高[8]，經過對比，本文采用D-最優實驗設計方法進行實驗設計。

基于方差分析方法的參數篩選，是在實驗設計得到有效的樣本數據后，從全局的角度出發，利用方差分析方法對整個樣本數據進行顯著性分析，篩選出對特征量影響顯著的參數，克服了基于靈敏度分析方法只計算了特征量局部靈敏度的嚴重不 足[8]。由此，本文采用基于方差分析方法來進行參數篩選。方差分析方法首先求得樣本數據中由因素引起的平方和A和由實驗誤差引起的平方和E，然后分別除以各自由度得到均方回歸(簡稱MSR)和均方殘差(簡稱MSE)，求出值。應用值檢驗 法[9]進行假設檢驗，找出顯著性參數，其計算如式(1)所示。對于給定的顯著水平，檢驗法則為：若≥1?α(?A, ?E)，則認為設計參數顯著，否則認為不顯著。

式中：?A和?e分別為因素和偏差的自由度。

根據結構特點及實驗設計方法的選擇，經過對比，本文選取如式(2)的二次多項式形式的響應面函數模型：

式中：E為樣本數據的誤差平方和；T為樣本數據的總偏差平方和；T為模型的總自由度；E為模型的偏差自由度；若2和2adj都接近于1且二者的差異較小，則認為響應面模型較好的擬合了樣本數據；若2adj和2pred都接近于1且二者之差在0.2以內，就表明所建立的模型能夠對未知數據進行良好的預測。

在經過上述步驟后，有限元模型修正轉化為求下式函數最優解的數學問題：

式中：為設計參數；?E為試驗值；?A為有限元模型分析值；λ為各特征響應量的權值，和為參數設計空間的下界和上界，本文采用遺傳算 法[11]對響應面函數進行優化求解。

綜上，本文采用基于響應面方法來進行橋梁有限元模型修正，在具體算法選取中，經過反復對比，在實驗設計方法選取中，采用D-最優實驗設計方法；在參數篩選中，采用了基于方差分析的方法；在響應面函數模型的選擇中，采用了二次多項式形式，并采用逐步回歸法對變量進行擬合得到響應面模型；最后，在響應面函數優化求解中，采用了遺傳算法。以上各種方法的組合，為考慮邊界約束條件的橋梁有限元模型修正研究奠定基礎。

2 大橋荷載試驗與自振特性分析

2.1 工程背景

本研究的依托大橋為雙層4車道高速公路、觀光通道兩用橋，橋型方案為塔梁分離的鋼桁加勁梁單跨懸索橋，大橋主跨為1 176 m，橋面寬27 m，該大橋為整條高速公路的控制性工程，橋型布置如圖1所示。

單位：cm

2.2 基于環境激勵的大橋動載試驗

課題組對該懸索橋進行了橋梁動載試驗，主要測試儀器包括8個加速度傳感器，8通道A/D采集器一臺，導線若干及筆記本電腦相關設備。為了保證傳感器與結構的同步移動，將傳感器與結構采用膠水固接，以期達到良好的同步振動效果。考慮大橋跨度和儀器設備，研究中采用移動測量法進行試驗，與傳統模態試驗方法相比，其具有試驗成本低、精度好、效率高和操作性好等優點[12]。測試中以每個吊桿下的主桁架下弦點為測點，以45號測點為參考點，每次進行4個測點的試驗，如(1+Z，3+Z，Y，1-Z，3-Z，Y，45+Z，Y)，(5+Z，7+Z，Y，5-Z，7-Z，Y，45+Z，Y)……(137+Z，139+Z，Y，137-Z，139-Z，Y，45+Z，Y)(Z表示橋梁豎向，Y表示橋梁橫向，+表示橋梁左側，?表示橋梁右側)。考慮到環境變化(主要為溫度變化)對結構自振特性的影響，測試時選擇了在氣溫變化不太明顯的陰天對橋梁進行了模態試驗，以減少環境變化所帶來誤差。測試方案如圖2所示。對實驗所測數據，采用NEXT/ ITD[13]法對大橋模態參數進行識別，得到各階模態實測結果如表1所示。

表1 初始有限元模型頻率計算結果與實測結果比較

圖2 測點布置

2.3 大橋初始有限元建模與自振特性分析

大橋初始有限元模型建立和自振特性計算由有限元通用軟件ANSYS完成，主梁鋼桁架桿件和混凝土主塔采用Beam188單元模擬，主纜和吊索采用Link10單元模擬。由于該橋的橋面系與鋼桁架主梁上的鋼縱梁相連，而鋼縱梁以簡支的方式與鋼桁架主梁連接，這種連接方式使橋面系與主桁架結構分離，不參與整體受力，因此建模中橋面系采用Mass21單元模擬其平動質量和扭轉質量，有限元模型如圖3所示。基于分塊蘭索斯方法對結構進行模態分析，得到前四階豎彎、一階橫彎和一階扭轉模態結果如表1所示。

由表1可知，實測各階頻率值稍大于初始有限元模型各階頻率計算值，說明橋梁實際剛度大于設計剛度。經研究，其主要原因在于，在初始有限元模型的建模過程中，根據設計圖紙，橋梁在縱向為自由平動狀態，而在實際橋梁結構中，包括伸縮縫、梁端橫豎橋向的支座等各種因素會對橋梁的縱向位移產生約束，橋梁兩端在縱向并不是簡單的自由平動狀態。此外，在多次試算過程中發現，縱向約束對橋梁自振特性影響較大。在后續的修正過程中，本文采用Combine14單元來模擬橋梁兩端縱向約束的作用，并以Combine14單元剛度值等為修正參數，以期達到更為真實的修正效果。

圖3 大橋初始有限元模型

3 大橋有限元模型修正

3.1 實驗設計

根據該懸索橋結構特點和工程實踐經驗，選取吊索彈性模量1，桁架彈模2，鋼桁架密度1，主纜彈模3，主纜密度2，塔柱混凝土彈模4和縱向約束彈簧單元剛度1等7個修正參數對初始有限元模型進行修正。經多次試算，各參數設計水平、空間范圍取值如表2所示。

確定參數范圍后，以大橋的前四階豎彎頻率1，2，3和4，一階反對稱橫彎頻率5及扭轉一階頻率6作為響應特征量，并根據前述的D-最優實驗設計方法進行實驗設計如表3所示，并利用有限元計算得到樣本值如表4所示。

表2 各參數取值范圍

表3 D-最優實驗設計

3.2 參數顯著性分析

根據前述的方差分析方法，應用數理統計中檢驗法分析所選參數對特征響應量的顯著性，計算各參數對特征響應量的水平值，并給定顯著水平=0.05，如圖4所示(由于參數較多，圖中僅顯示部分參數的顯著性)，縱坐標表示值，橫坐標表示各設計參數。限于篇幅，本文僅以一階正對稱豎彎響應面模型為例進行說明。

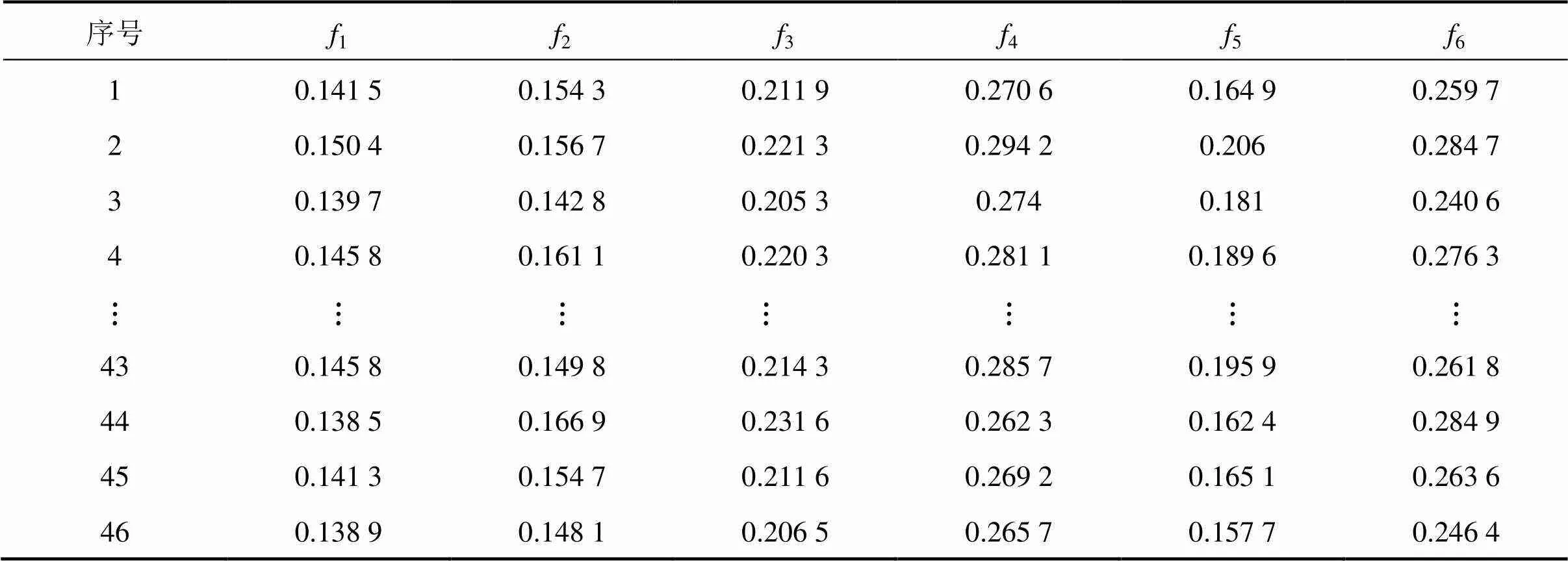
表4 有限元計算樣本值

圖4 各參數對一階正對稱豎彎頻率顯著性檢驗

由圖4可知，各參數的一次項對一階正對稱豎彎頻率的影響均比較顯著，說明待修正參數的選取能夠符合要求，在響應面函數中，一次項占主要成分，對響應面模型的精度影響較大。對含有1參數的交叉項，除12外，特征量響應均不大。說明1參數對特征量的影響相對較小。對含有2參數的交叉項，除21外，均對特征量產生較大影響，說明2參數對特征響應量的影響比較顯著。同理，含有1參數的交叉項，21，13，12均對一階頻率產生較顯著影響。對二次項，2，3和1均產生比較顯著的影響。對于影響特別顯著的參數，由于其值較小的變化會引起特征頻率值發生明顯的改變，因此對其參數范圍的選取應該更加慎重。

3.3 響應面函數擬合與精度檢驗

1=0.129+7.565×10?4×1+0.01×2?6.641×

10?7×1+4.510×10?3×3?1.102×10?6×2+

6.813×10?5×4+1.176×10?3×1?1.297×10?4×

1×2?1.387×10?7×2×1+1.273×10?3×2×

3?1.606×10?7×2×2+1.229×10?4×2×1+

7.021×10?8×1×3+1.955×10?11×1×2+

5.101×10?8×3×2+9.969×10?9×3×4?

表5 各階響應面模型精度檢驗

3.4 模型修正

利用得到的各階響應面方程，構造如式(6)和式(7)的目標函數，根據前述的遺傳算法對優化函數進行優化求解，本文采用單目標函數進行修正，并假定各階頻率的差異性相同，即各階響應面函數的權值均取為1，各階頻率修正結果如表6所示，各參數修正結果如表7所示。

表6 各階頻率修正結果

表7 參數修正結果

基于以上修正過程得到的模型修正結果，由表6可知，頻率誤差值較修正前有了較大的改善，各階頻率相對誤差值都在10%以內，且對三階正對稱豎彎頻率有良好的預測，說明取得了比較良好的修正效果。對于各參數的修正量，均保持在合理范圍內。吊索彈模、鋼桁架彈模、主纜彈模和混凝土塔柱彈模均有不同程度的增加。其中，以主纜彈性模量改變量為16.5%最為突出，原因有2：其一，這與構件的實際受力大小有關，在懸索橋結構中，主纜是最為主要的受力構件，也是受力最大的構件，隨著主纜應變的增大，主纜剛度也會適當的增大；其二，主纜護欄由4根高強鋼絲構成，會對主纜提供一定的剛度，這在初始模型建模過程中是沒有考慮的。同樣，對于吊索彈模、鋼桁架彈模和混凝土塔柱彈模，受力的大小、橋面板與塔柱中的鋼筋骨架也會使相應構件的剛度增加。對于鋼桁密度和主纜密度也有不同程度的增加，這是由于在初始建模過程中，沒有考慮主纜上鎖夾的質量和主梁上人行道觀光橋及其他難以考慮到的附屬設施質量。修正結果中等效彈性模量和等效密度的增加能夠體現實際情況。同時，為考慮橋梁縱向剛度參數，本文采用縱向彈簧單元進行模擬并對其剛度進行修正，從而使修正后的有限元模型能夠合理考慮懸索橋實際的邊界約束條件。反之，經過反復對比試算表明，當模型修正過程中不考慮橋梁縱向約束剛度時，修正后的各個參數值明顯偏離正常值，且有限元模型的修正結果也與試驗值誤差較大。以上結果表明，考慮邊界約束條件修正在該類型大橋有限元模型修正中起著至關重要的作用。

綜上所述，修正后的有限元模型各個參數均較合理，反映并驗證了前述結合響應面方法并根據大橋特點選取的一系列算法組合在考慮邊界約束條件的有限元修正模型中的有效性，該修正有限元模型能夠作為大橋結構的基準有限元模型，并為下一步的大橋結構響應分析提供基礎。

4 結論

1) 忽略橋梁結構各構件尺寸的變化，以材料特性與邊界條件等為修正參數，采用響應面方法對初始有限元模型進行修正，最大相對誤差為8.52%，最小相對誤差為1.06%，較修正前有了較大的改善，且各參數修正量均在合理范圍內，驗證了響應面方法在有限元模型修正中的有效性和高效性。

2) 在以往的修正案例中，往往忽略了對邊界條件約束的影響，本文以特殊的塔梁完全分離的某懸索橋結構為依托，考慮縱向約束的影響，用Combine14單元模擬橋梁的縱向約束，以Combine14單元的剛度值為修正參數對初始有限元模型進行修正，修正后的模型更符合實際情況且精度更高。以上結果反映并驗證了本文基于響應面方法并結合該懸索橋特點選取的一系列算法組合在考慮邊界約束條件的有限元修正模型中的有效性，可以為此類型的懸索橋結構有限元模型修正提供參考。

3) 修正后的有限元模型可以一定精度預測修正頻段外的模態頻率，進一步說明修正后的有限元模型有良好的預測功能，修正后的有限元模型更能夠體現結構的實際狀態，可以作為該懸索橋結構的基準有限元模型。

[1] LIU Yang, YANG Changxi, TAN Zhicheng. Hybrid element-based virtual distortion method for finite element model updating of bridges with wide-box girders[J]. Engineering Structures, 2017(143): 558?570.

[2] 單德山, 孫松松, 黃珍, 等. 基于試驗數據的吊拉組合模型橋梁有限元模型修正[J]. 土木工程學報, 2014, 47(10): 88?95. SHAN Deshan, SUN Songsong, HUANG Zhen, et al. Finite element model updating of combined cable-stayed suspension model bridge based on experimental data[J]. China Civil Engineering Journal, 2014, 47(10): 88?95.

[3] 任偉新, 陳華斌. 基于響應面的橋梁有限元模型修正[J]. 土木工程學報, 2008, 41(12): 73?78. REN Weixin, CHEN Huabin. Finite element model updating of bridge based on response surface[J]. China Civil Engineering Journal, 2008, 41(12): 73?78.

[4] 魏錦輝, 任偉新. 結構有限元模型修正的自適應響應面法[J]. 振動與沖擊, 2013, 32(8): 114?119. WEI Jinhui, REN Weixin. Adaptive response surface method for finite element model modification of structures[J]. Journal of Vibration and Shock, 2013, 32(8): 114?119.

[5] 周林仁, 歐進萍. 基于徑向基函數響應面方法的大跨度斜拉橋有限元模型修正[J]. 中國鐵道科學, 2012, 33(3): 8?15. ZHOU Linren, OU Jinping. Finite element model updating of long-span cable-stayed bridge based on radial basis function response surface method[J]. China Railway Science, 2012, 33(3): 8?15.

[6] 李剛. 基于靜動力響應面的梁橋有限元模型修正方法研究[D]. 成都: 西南交通大學, 2018. LI Gang. Research on finite element method updating for beam bridge based on static and dynamic response surface[D]. Chengdu: Southwest Jiaotong University, 2018.

[7] 王蕾, 郁勝, 李賓賓, 等. 基于徑向基神經網絡的橋梁有限元模型修正[J]. 土木工程學報, 2012(增2): 11?15. WANG Lei, YU Sheng, LI Binbin, et al. Revision of finite element model of bridge based on radial basis function neural network[J]. China Civil Engineering Journal, 2012(Suppl 2): 11?15.

[8] ZONG Zhouhong, LIN Xiaosong, NIU Jie. Finite element model validation of bridge based on structural health monitoring—Part I: Response surface-based finite element model updating[J]. Journal of Traffic and Transportation Engineering (English Edition), 2015, 2(4): 258?278.

[9] Mertler C A, Reinhart R V. Advanced and multivariate statistical methods: practical application and interpretation[M]. 6th ed. London: Routledge, 2016.

[10] Fox J. Applied regression analysis and generalized linear models[M]. 3rd ed. Los Angeles: SAGE Publications,Inc, 2015.

[11] Corrado C, Chiara B, Claudio A. Dynamic and static identification of base-isolated bridges using genetic algorithms[J]. Engineering Structures, 2015(102): 80?92.

[12] 彭濤. 基于環境激勵的大跨度橋梁模態分析及應用研究[D]. 長沙: 長沙理工大學, 2007. PENG Tao. Modal analysis and application research of long-span bridges based on environmental excitation[D]. Changsha: Changsha University of Science and Technology, 2007.

[13] SONG Xingyu, MA Hongwei, WANG Kun. A new developed modal parameter identification method based on empirical mode decomposition and natural excitation technique[J]. Procedia Engineering, 2017(199): 1020? 1025.

(編輯 蔣學東)

Finite element model updating for a suspension bridge considering the boundary constraint conditions

ZOU Xiangnong1, LONG Junxian1, YANG Degao2, HU Peng2, HAN Yan2

(1. China Railway Wuhan Survey and Design & Institute Co., Ltd, Wuhan 430074, China; 2.,,410114, China)

The effects of boundary condition constraints are always ignored in the previous studies. To consider the differences between the boundary condition constraints in the bridge’s initial finite element model and those in the real bridge, a tower-beam separation suspension bridge was taken as the engineering background in the present study. Based on the dynamic loading test results in the field measurements, the Combine14 element was adopted to model the longitudinal constraint conditions of stiffening girders of the suspension bridge. By combining the response surface method with the bridge’s features, a series of algorithms were selected to consider the effects of boundary condition constraints on the bridge’s initial finite element model, and then to update its initial finite element model. The results show that the updated results with considering the effects of boundary condition constraints are much closer to the field measurements results of the suspension bridge, and the updating values of all updating parameters are in reasonable ranges, indicating that the above method of considering the effects of boundary condition constraints is effective in the finite element model updating. The updated finite element model can be taken as the baseline finite element model for the suspension bridge with providing the basic for further response analysis of the bridge.

finite element model updating; boundary constraint conditions; response surface method; dynamic loading test

10.19713/j.cnki.43?1423/u.2019.05.015

U446

A

1672 ? 7029(2019)05 ? 1223 ? 08

2018?10?31

國家自然科學基金資助項目(51878080, 51822803)；湖南省自然科學基金資助項目(2018JJ3538)；湖南省教育廳科研資助項目(17C0056)

胡朋(1985?)，男，湖北黃岡人，副教授，博士，從事大跨度橋梁抗風設計理論研究；E?mail：hupeng@csust.edu.cn