幼兒心理數線的發展：估計準確率與模式背后的策略 *

臧蓓蕾 張 俊 顧榮芳

(南京師范大學教育科學學院，南京 210097)

1 引言

心理數線（mental number line）是對數字在大腦中表征的比喻，是數量表征的一種形式（Dehaene, Bossini, & Giraux, 1993）。已有關于心理數線的研究主要采用數線任務（number-line task）進行探究（Link, Huber, Nuerk, & Moeller,2014; Simms, Clayton, Cragg, Gilmore, & Johnson,2016）。目前使用數線任務研究心理數線主要有兩個發現：第一是兒童的年齡越大，數線估計的正確率越高；第二是兒童的表現反映了表征模式的變化，年幼兒童會高估小數字，低估大數字，表現出對數模型。隨著兒童年齡的增長，兒童會逐漸更加平均地分配數字，表現出線性的模型（Booth & Siegler, 2006; Siegler & Booth, 2004）。對數模型是指位于數字線較小一端的數字比較大一端的數字擁有更大的心理距離，實際數值大小與心理數值大小是以對數關系對應的；線性模型則是指實際數值大小與心理數值大小是線性對應的，數字的心理距離和理論距離是線性相關的（劉國芳, 辛自強, 2012）。已有研究大多認為兒童會逐漸從對數估計模型轉換到線性估計模型（ Booth & Siegler, 2006; Siegler & Opfer, 2003），然而近年來越來越多的研究者對此提出質疑，指出雙線性、多線性等其它估計模型的存在（Bouwmeester & Verkoeijen, 2012; Ebersbach, Luwel, Frick,Onghena, & Verschaffel, 2008; Slusser, Santiago, &Barth, 2013）。

有研究者意識到數線估計模型差異背后的意義，轉而在紛繁復雜的模型之爭背后尋找可能的差異根源。Siegler 和Opfer（2003）在研究中發現估計的準確率與數量的大小相關，兒童會使用數字的分界點對數線進行劃分，由此認為兒童可能會運用一定的策略進行數線估計。國內也有學者對5～6 歲幼兒在0～100 數線范圍內的估計能力、工作記憶能力對數線估計結果的影響進行了研究，結果發現幼兒是一個“靈活的策略使用者”，傾向于使用中點和端點策略進行數線估計（劉國芳, 辛自強, 2012）。作為一種復雜的認知過程，數線估計需要幼兒多方面認知能力的參與。已有研究認為幼兒數量估計的策略包括眼球效應、基準比較等策略（Crites, 1992），然而幼兒數線估計與數量估計又有所不同。幼兒究竟是如何進行數線估計的，是否可能會表現出相關的估計策略？如果具有估計策略，它們與數線估計的準確率、估計模型是否有聯系？

首先，已有關于心理數線研究的對象多為西方國家5～6 歲及以上年齡階段的兒童和成人，數線估計范圍為0～100 或0～1000（Opfer, Thompson,& Kim, 2016; Slusser et al., 2013）。極少有研究向另一端延伸，即探究更小的年齡階段和更小的數線估計范圍（1～5/1～10/1～20）中心理數線的發展特點（Ramani & Siegler, 2008; Siegler & Ramani,2008），以了解兒童在早期對數量表征及數量關系的認知特點。國內關于心理數線的研究并不多，特別是幼兒心理數線發展的研究更少。心理數線是數概念發展的重要組成部分，與各種數學能力的發展密切相關（Schneider, Grabner, & Paetsch,2009）。由于文化傳統等各方面因素的影響，中國幼兒的數量表征能力發展水平高于西方同齡幼兒（Laski & Yu, 2014; Siegler & Mu, 2008），因此有必要對學前期幼兒的心理數線發展特點進行探究。

其次，已有研究的數線估計任務情景都較為單一，即只采用相同數線跨度的一種估計情景，極少有研究對不同的情景進行對比（Laski & Yu,2014; Xu, Chen, Pan, & Li, 2013）。再次，在以往關于心理數線的研究中，大多數研究只對參與者的數線估計結果進行量化的分析，而缺少對參與者的數線估計過程進行關注。已有關于兒童心理數線的研究多為估計準確率和估計模式的研究，極少有對兒童數線估計策略的研究，也并未有對更小年齡的幼兒在更小的數線估計范圍內的估計策略的探究。

由于3～5 歲幼兒具有動作思維的認知發展特點，幼兒在完成數線估計任務的過程中可能會有外顯的策略表現情形。因此本研究首先將對3～5 歲幼兒在兩種不同估計情景中的三個不同數線范圍（1～5/10/20）心理數線的發展特點進行探究，并在幼兒完成數線估計任務的基礎上，通過對幼兒策略使用情況的觀察以及與幼兒對話詢問的方式分析不同年齡階段幼兒在不同估計情景中進行數線估計所使用的策略，初步探究幼兒在數線估計任務中的策略使用情況及策略使用與幼兒心理數線發展水平之間的關系，從而更加深入立體地了解幼兒心理數線的發展特點。

2 研究方法

2.1 研究對象

研究者在N 市兩所普通公辦幼兒園分別選取小班幼兒41 名（平均月齡51 個月），中班幼兒40 名（平均月齡63 個月），共81 名幼兒參與心理數線估計策略的研究，具體見表1。

表 1 參與研究兒童人數及平均月齡分布表

2.2 研究工具

本研究采用Siegler 和Booth 等已有研究中采用的NP（number-to-position, 數字到位置）數線估計任務（Siegler & Booth, 2004; Siegler & Mu, 2008;Simms, Muldoon, & Towse, 2013），已有研究中使用數線估計任務的研究對象多為6 歲以上的兒童，數線估計任務中的數線范圍為0～100。研究者結合研究目的，考慮到3～5 歲幼兒數概念及認知發展水平，對數線估計任務的范圍和操作形式進行了調整，將數線范圍調整為0～5/10/20，操作形式更加游戲化，以便于幼兒理解和操作。

測查材料為一張印有數線的1/4 大小的A4 紙（長為297 mm, 寬為52.5 mm）操作單，數線左邊為數字1，右邊為數字X（X=5/10/20），數線中間上方20 mm 處有一個待估計數字N（1＜N＜X）。

測查材料分為兩組，第一組（情景一）測查材料為跨度相同（171 mm），數距不同的數線估計任務單，即1～10 和1～20 的數線長為171 mm，1～5 的數線長為172 mm（為便于精確測量和計算,故取172 mm, 數距長度為43 mm）。

第二組（情景二）測查材料為跨度不同，數距相同（9 mm）的數線估計任務單，即1～5 數線長為36 mm，1～10 的數線長為81 mm，1～20 的數線長為171 mm，數距都為9 mm。第一組（情景一）測查材料1～20 數線范圍的操作單與第二組（情景二）測查材料1～20 數線范圍的操作單相同，數線長為171 mm，數距為9 mm。每組包括1～5、1～10、1～20 三個數線范圍的共17 張測查單。

被估計數字的選擇主要有以下兩個方面的考慮，一方面根據中班、小班幼兒的實際情況，測查時間不宜過長，因而數線范圍內的每個數字不可能都被測查；另一方面，研究者參考已有研究測查任務中選擇的被估計數字。因而1～5 數線要估計的目標數字為：2、3、4（共3 個）；1～10數線要估計的目標數字為：2、3、4、6、7、8、9（共7 個）；1～20 數線要估計的目標數字為：3、4、6、8、12、14、17（共7 個）。

每個估計的數字都是在一張單獨的操作單上，每個數線范圍內需要估計的數字是隨機的順序。40 名幼兒參與情景一的測查，41 名幼兒參與情景二的測查。

2.3 研究步驟

研究者首先對幼兒進行數線估計任務的測查，在每一次測查前，主試都會口頭提醒以下指導語：“數字寶寶1 到5/10/20 排在這條線上，這邊是數字寶寶1，這邊是數字寶寶5/10/20，數字寶寶N 回來了，你覺得它應該排在哪里?”測查后，研究者對每位幼兒在三個不同數線范圍內都進行了策略的詢問：“你是怎么知道的?”在幼兒操作過程中，研究者觀察并記錄了每一位幼兒的數線估計過程和策略。

測查之后，研究者一方面對測查結果進行量化統計分析，確定幼兒數線估計準確率及估計模式；另一方面，研究者根據測查時對幼兒回答的記錄及后期視頻的回放和觀看，將幼兒表述策略的話語進行記錄和整理，并對這些話語進行編碼和分類。研究者試圖通過對策略的記錄和分析，在量化的數據結果和質性的策略記錄中尋找可能的對接點，探究幼兒心理數線的發展與其策略使用之間的相關性。

3 結果與分析

3.1 數線估計策略特點

研究者通過對策略的梳理和編碼，發現幼兒一共表現出六種不同的數線估計策略，分別為：“不知道”、“其它”、“視覺線索”、“數數”、“參照端點”、“數字關系”，其中后四種為有效的估計策略。

“不知道”是指幼兒不進行回答或者直接回答“不知道”、“不清楚”；“其它”策略是指幼兒回答“猜的”、“就是知道”等策略，或者回答的“策略”與數線估計任務不相關，例如幼兒回答“畫瓢蟲知道的”，“永遠超級知道”等；“視覺線索”策略是指幼兒通過觀察數線完成數線估計任務，或者回答“我看出來的”，“剛才看到的”等；“數數”策略是指幼兒回答和數數相關的策略，例如幼兒回答“因為1、2、3、4、6”，“會數數知道的”等等，或者幼兒表現出數數（包括默數）的行為；“參照端點”策略是指幼兒參照數線兩端的數字，例如幼兒回答“看20 在這里，8 應該離20 遠一點”，“看10 在這里”，“因為20 后面有數字，14 就該在這里”；“數字關系”是指幼兒運用數字之間的關系進行推斷，例如幼兒回答“7 在8 的旁邊”，“3 在中間，2 在這邊”，“因為9 是在8 的后面”。各年齡階段幼兒在不同情景和數線范圍的數線估計任務中使用的策略種類頻數及百分比具體見表2。

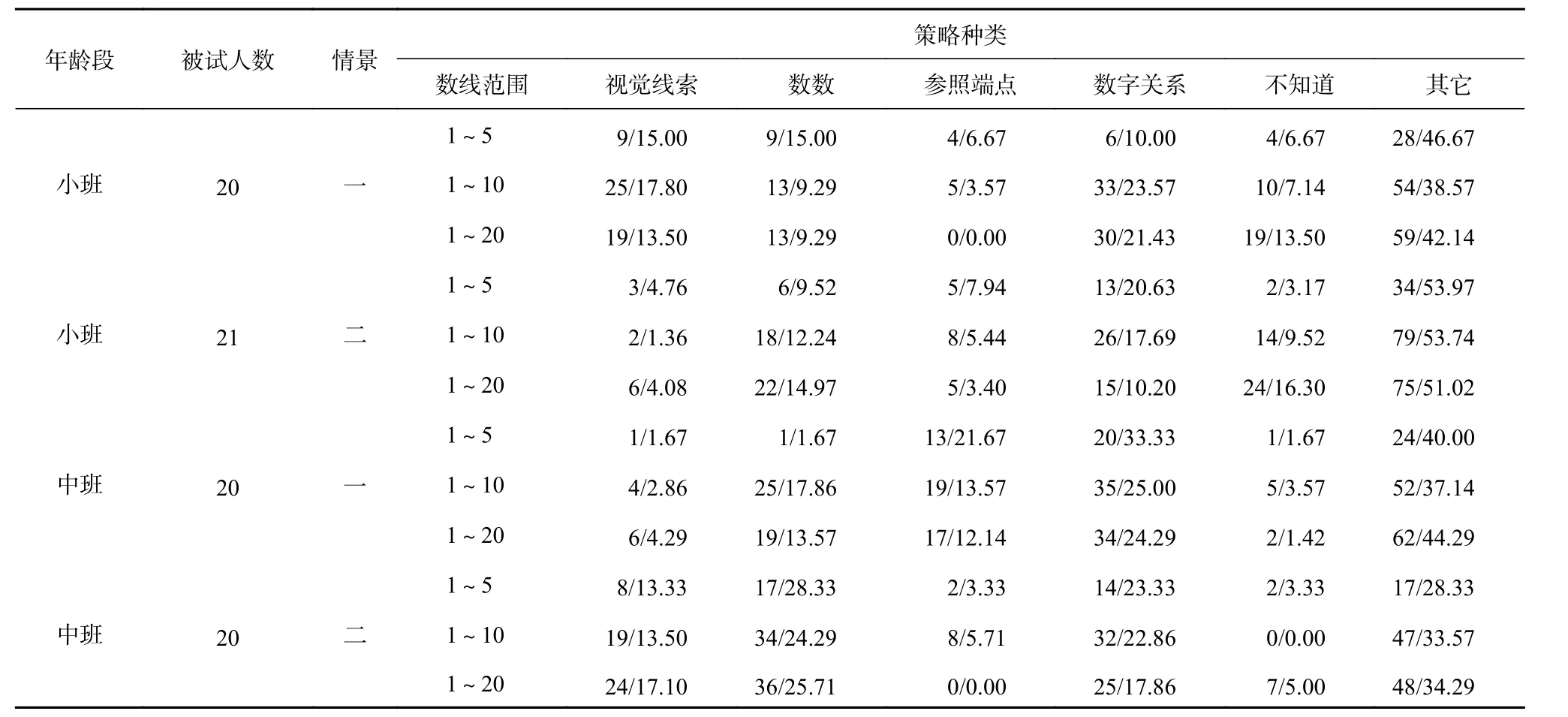
表 2 幼兒數線估計策略頻數及百分比

綜合各個數線范圍內不同年齡階段幼兒在不同數線估計情景中使用策略差異的分析結果，可以發現：與中班幼兒相比，小班幼兒較多使用“不知道”策略，比例隨著數線范圍的擴大而增長，尤其在1～20 數線范圍內的兩種不同情景中，小班幼兒使用此策略顯著多于中班幼兒（χ2=13.76, df=1, p＜0.01, Φ=0.81; χ2=9.32, df=1, p＜0.01,Φ=0.55）；幼兒在三個數線范圍內對“其它”策略使用頻率都較高，小班幼兒在情景二的三個數線范圍內對此策略的使用頻率顯著高于中班幼兒（χ2=5.67, df=1, p＜0.05, Φ=0.33; χ2=8.13, df=1, p＜0.01,Φ=0.26; χ2=5.93, df=1, p＜0.05, Φ=0.22）；在三個不同數線范圍內，小班幼兒在情景一中使用“視覺線索”策略的頻率顯著高于情景二，而中班幼兒在情景二中使用此策略的頻率較高；關于“數數”策略，幼兒在情景二的使用頻率顯著高于情景一，中班幼兒使用頻率顯著高于小班幼兒（χ2=13.19, df=1, p＜0.01, Φ=0.25; χ2=12.21, df=1, p＜0.01,Φ=0.24）；幼兒使用“參照端點”策略在1～5 數線范圍內比例最高，隨著數線范圍的擴大而逐漸降低，中班幼兒在不同數線范圍內情景一的使用頻率顯著高于情景二（χ2=8.07, df=1, p＜0.01, Φ=0.73;χ2=4.48, df=1, p＜0.05, Φ=0.41）；關于“數字關系”策略，中班幼兒在各情景中普遍多于小班幼兒，“數字關系”在1～10 數線范圍內比例最高。

總體看來，按照使用的頻數及百分比，從高到低的次序依次為：“其它”、“數字關系”、“數數”、“視覺線索”、“參照端點”、“不知道”。小班幼兒較多使用的是“不知道”和“其它”的策略，而中班幼兒使用有效策略的頻率顯著提高。

3.2 主要數線估計策略與絕對誤差百分比

為了解幼兒數線估計策略與其估計準確度之間的關系，研究者對每位幼兒在各個數線范圍內的估計策略進行歸納，以每位幼兒在測查中使用頻率最高的策略為準，確定每位幼兒在某一數線范圍內的主要估計策略。采用單因素方差分析，了解不同數線范圍內每位幼兒的絕對誤差百分比（percent absolute error，PAE）均值與其主要估計策略是否存在差異。在本研究中，絕對誤差百分比為：|（估計的數的長度—被估計的數的長度）/數線總長度|。絕對誤差百分比越低，表明估計的準確率越高。方差分析結果表明：在1～5 數線范圍內，幼兒估計的絕對誤差百分比不存在顯著的策略差異，F（5, 75）=0.77，η2=0.05，p＞0.05；在1～10 數線范圍內，幼兒估計的絕對誤差百分比不存在顯著的策略差異，F（5, 75）=0.35，η2=0.02，p＞0.05；在1～20 數線范圍內，幼兒估計的絕對誤差百分比存在顯著的策略差異，F（5,75）=3.30，η2=0.18，p＜0.05。事后分析的多重比較結果顯示，“不知道”策略和其它五種策略（“視覺線索”、“數數”、“參照端點”、“數字關系”、“其它”）的絕對誤差百分比差異顯著，p＜0.05；“其它”策略和“數數”策略的絕對誤差百分比差異顯著，p＜0.05。具體見表3。

3.3 主要數線估計策略與數線估計模式

研究者通過對幼兒數線估計任務數據結果的統計分析，借助Mplus7.0 軟件進行潛在類別分析（latent class analysis），確定每位幼兒的心理數線估計模式。潛在剖面分析（latent profile analysis）是潛在類別分析的一類，具有連續潛在類別指標的潛在類別分析常被稱為潛在剖面分析。在潛在剖面分析中，阿凱克信息準則（AIC）、貝葉斯信息準則（BIC）、貝葉斯準則校正指標（ABIC）數值越低，信息熵Entropy（取值介于0～1）越高表示模型的擬合度越高。此外，LMR（lo-mendellrubin likelihood ratio test, 羅夢戴爾魯本校似然比）和BLRT（bootstrapped likelihood ratio test,Bootstrapped 似然比檢驗）能夠輔助比較和判斷最佳類別模型，如果LMR 和BLRT 指標的p 值達到顯著性水平，則表示K 個類別的優于K-1 個類別（Muthén & Muthén, 2012）。

從表4、表5 和表6 可以看出，AIC、BIC 值隨著分類數量的增加而不斷下降，較低的AIC、BIC 值，較高的Entropy 值和顯著的LMR 和BLRT預示著模型的擬合度較好。綜合上述指標，幼兒在1～5 數線范圍中4 個類別模型的LMP p 值顯著（p＜0.05），表明4 個類別的模型優于3 個類別的模型，且4 個類別模型的Entropy 指標最高，因此選擇4 個潛在類別的分類；在1～10 數線范圍中各個類別模型的LMP p 值都不顯著，但是3 個類別的Entropy 指標最高，因此選擇3 個潛在類別的分類；在1～20 數線范圍中各個類別模型的LMP p 值都不顯著，但是2 個類別的Entropy 指標最高，因此選擇2 個潛在類別的分類。根據選定的潛在類別分類，在Mplus 中導出潛在剖面圖，坐標調整后的不同數線范圍各個類別的LCA 剖面圖見圖1。

表 4 幼兒1 ～ 5 數線范圍的潛在剖面（LPA）的各項指標比較

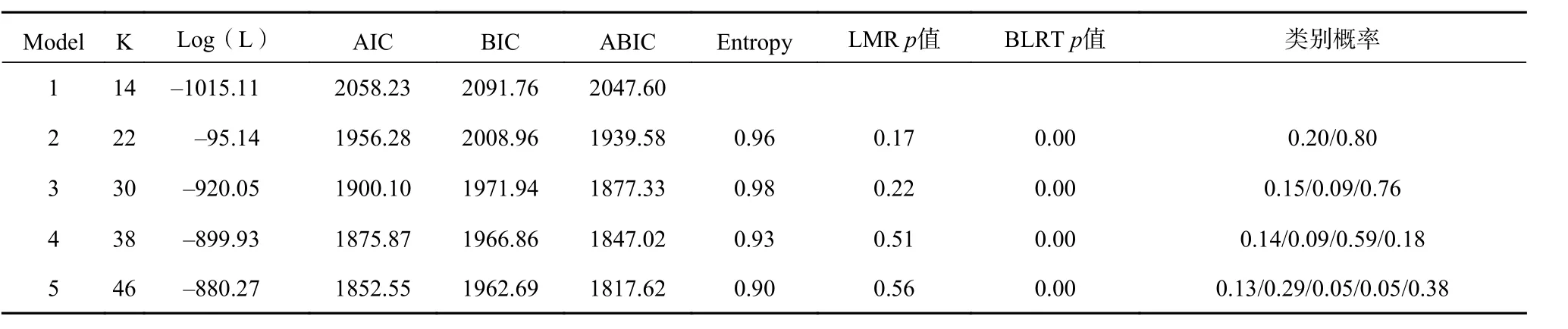
表 5 幼兒1 ～ 10 數線范圍的潛在剖面（LPA）的各項指標比較

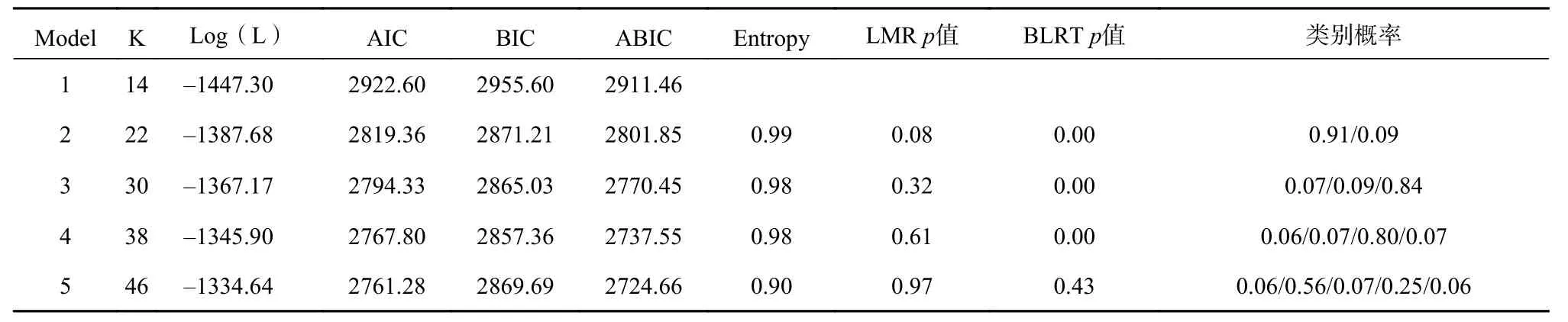
表 6 全體幼兒1 ～ 20 數線范圍的潛在剖面（LPA）的各項指標比較

研究者根據潛在剖面圖呈現出的估計模式及已有研究中常見的估計模式進行命名。由圖1 可以看出，在1～5 數線范圍內，四個類別的估計模式分別為：小數低估、大數高估的“拉伸模式”（Class1-7%）、基本接近標準值的“標準線性模式”（Class2-56%）、整體低估而呈線性的“非標準線性模式”（Class3-36%）和不規則的“其它模式”（Class4-1%）；在1～10 數線范圍內，三個類別的估計模式分別為整體低估而呈線性的“非標準線性模式”（Class1-15%）、不規則的“其它模式”（Class2-9%）和基本接近標準值的“標準線性模式”（Class3-76%）；在1～20 數線范圍內，兩個類別的估計模式分別為：對數模式（Class1-91%）和其它模式（Class2-9%）。將幼兒在各個數線范圍內進行數線估計任務時所使用的主要策略和其對應的估計模式進行統計，結果如表7 所示。從橫向來看，每種估計模式使用頻數最高的策略類別集中在“數字關系”和“數數”兩種策略。尤其是在標準線性模式、非標準線性模式以及對數模式這三種估計模式中，“數字關系”策略的使用頻率較高。從縱向來看，除了“不知道”這一類別外，其余四種策略種類中頻數最高的都是標準線性模式。在標準線性估計模式中，使用頻率較高的也是“數字關系”、“數數”策略。可見，達到標準線性估計模式的幼兒使用各種有效策略的頻率較高，而“數字關系”和“數數”策略則是幼兒主要估計模式中最為常用的策略。

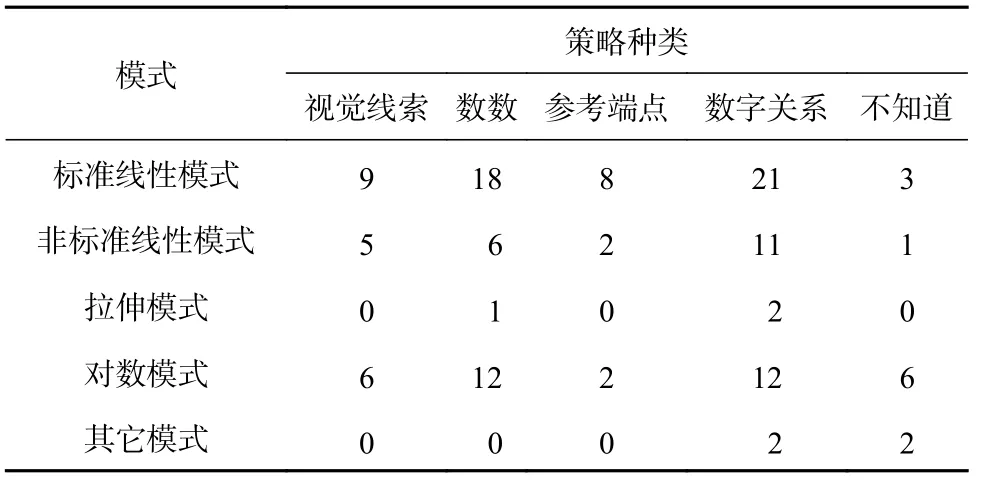
表 7 各估計模式策略種類分布表

4 分析與討論

4.1 幼兒心理數線估計使用策略的特點

4.1.1 幼兒數線估計的策略具有多樣性的特點

幼兒在進行數線估計過程中展現了豐富的策略，一方面體現在策略種類的多樣化，研究者通過編碼歸類，共總結六種策略。另一方面，策略的多樣性體現在幼兒對策略運用的多樣化。測查中發現，同一幼兒在不同范圍的數線估計任務中使用的策略有所不同，在同一數線范圍不同數字的數線估計任務中使用的策略也有不同。部分幼兒在三個數線范圍的17 個估計數字中能夠表現出3～4 種不同的估計策略。

4.1.2 幼兒數線估計的策略具有差異性

首先，幼兒數線估計策略使用具有年齡差異。研究發現，小班幼兒使用“不知道”、“其它”兩種較低水平策略的頻率高于中班幼兒；而中班幼兒使用“數數”、“數字關系”兩種較高水平策略的頻率高于小班幼兒。在小班幼兒群體中，“不知道”和“其它”策略所占比例較大可能與幼兒的認知發展水平和語言表達能力有關。小班幼兒還不具備策略表達能力，不能對自身的思維進行反思，但是幼兒又要盡力給研究者一個答案，因此會出現各類和問題幾乎沒有相關性的答案。另一方面也可能是幼兒沒有理解研究者提問的本意，不理解研究者的問題，而沒有從數線估計任務本身來回答。但是測查中也發現部分小班幼兒能夠使用“數數”、“數字關系”的策略，這也體現了幼兒心理數線發展的年齡差異性。中班幼兒對“數數”和“數字關系”策略的運用普遍多于小班幼兒表明，此年齡階段幼兒開始認識到數量關系可以通過“數數”的方式來梳理和判斷，而不僅僅是用眼睛看。這一變化趨勢符合幼兒數概念的發展趨勢，4 歲幼兒開始意識到數數和數字的位置是相關的（Sarama & Clements,2009），體現出此年齡階段幼兒對數序、數距和數量關系的關注。

其次，幼兒數線估計策略使用具有情景差異。由于情景設置的不同，部分估計策略在特定情景中的使用頻率顯著高于其它策略，例如中班幼兒在情景一中使用“參照端點”策略顯著高于情景二。

最后，幼兒數線估計策略使用具有數線范圍差異。隨著數線范圍的擴大，“不知道”和“其它”策略的使用比例在不斷增加；“參照端點”策略使用的比例在不斷降低。這表明一些策略的使用受到數線范圍影響。

4.2 估計策略與絕對誤差百分比

研究發現，在1～5 和1～10 數線范圍內，幼兒數線估計的絕對誤差百分比不存在顯著的策略差異。在1～20 數線范圍內存在顯著的策略差異，運用“不知道”策略的絕對誤差百分比顯著高于其它五種策略，即估計準確率顯著低于其它五種策略；運用“其它”策略的絕對誤差百分比顯著高于“數數”策略。

“不知道”策略是指幼兒不能夠回答自身策略。這部分幼兒可能并不理解研究操作或者不知道如何表達自己的策略，這一方面與幼兒的語言理解和表達能力有關，另一方面也可能與其日常的數學教育等有關。除了“不知道”策略，運用“其它”策略的幼兒在1～20 數線估計中的準確率顯著低于“數數”策略。相比于“不知道”、“其它”策略，“數數”是一種更加有效的估計策略。一方面有效的策略能夠輔助幼兒進行數線估計，提高數線估計的準確率。另一方面，關注到數字和數量關系的策略能夠有效幫助幼兒降低估計錯誤。這也說明數數能夠幫助幼兒建立對數字關系的理解，幫助幼兒逐漸發展心理數線，是心理數線建立過程中的重要策略。

4.3 估計策略與估計模式

首先，估計策略能夠影響估計模式。例如中班幼兒在情景一中對“參照端點”策略的使用頻率顯著高于其它，其中1～5 數線范圍的使用頻率最高。而估計模式統計結果也顯示，中班幼兒在1～5 數線范圍內表現出較高比例的“拉伸模式”，這一模式的主要形成原因就是幼兒對兩端端點的關注，這與幼兒整體的估計策略是緊密相關的。“參照端點”策略和“拉伸模式”表明幼兒認識到數量的起點和終點，是一種對數量范圍的關注，認識到集合是有限的，而不是毫無邊界的，表明幼兒開始具有初步的數量關系概念。

其次，各種估計模式中使用比例較高的是“數字關系”和“數數”策略。尤其是在標準線性模式、非標準線性模式以及對數模式這三種估計模式中，“數字關系”策略的使用頻率最高。可見，“數字關系”和“數數”是幼兒數線估計中重要且有效的策略，對“數字關系”的理解和“數數”的掌握可以幫助幼兒把握數序和數距的關系。這也在一定程度上說明，能夠熟練地數數和掌握數字之間的關系對于幼兒建立和發展心理數線具有重要的意義。

最后，“標準線性模式”中各種有效策略運用的比例最高。除了“不知道”策略之外，“標準線性模式”中其余四種策略的使用頻率都高于其它模式類別。可見，達到標準線性估計模式的幼兒能夠使用各種有效策略進行數線估計。“標準線性模式”是最為接近標準值的估計模式，達到這一模式是幼兒心理數線形成的標志。這一結果一方面表明運用有效的估計策略能夠幫助幼兒形成線性估計模式，建立心理數線；另一方面也表明能夠準確表達自身策略的幼兒，其估計模式水平更高，向標準線性模式趨近。

5 結論

本研究條件得到以下結論：（1）3～5 歲幼兒在數線估計任務中表現出豐富多樣的估計策略，包括“視覺線索”、“數數”、“參照端點”、“數字關系”等策略；（2）幼兒數線估計策略具有年齡差異、情景差異和數線范圍的差異；（3）估計策略與數線估計準確率、數線估計模式密切相關。

參 考 文 獻

劉國芳, 辛自強. (2012). 數字線估計研究: “模型”背后的策略. 心理研究, 5(2), 27–33, doi: 10.3969/j.issn.2095-1159.2012.02.004.

Booth, J. L., & Siegler, R. S. (2006). Developmental and individual differences in pure numerical estimation. Developmental Psychology,42(1), 189–201, doi: 10.1037/0012-1649.41.6.189.

Bouwmeester, S., & Verkoeijen, P. P. J. L. (2012). Multiple representations in number line estimation: A developmental shift or classes of representations? Cognition and Instruction, 30(3), 246–260, doi:10.1080/07370008.2012.689384.

Crites, T. (1992). Skilled and less skilled estimators' strategies for estimating discrete quantities. The Elementary School Journal, 92(5), 601–619,doi: 10.1086/461709.

Dehaene, S., Bossini, S., & Giraux, P. (1993). The mental representation of parity and number magnitude. Journal of Experimental Psychology:General, 122(3), 371–396, doi: 10.1037/0096-3445.122.3.371.

Ebersbach, M., Luwel, K., Frick, A., Onghena, P., & Verschaffel, L. (2008).The relationship between the shape of the mental number line and familiarity with numbers in 5-to 9-year old children: Evidence for a segmented linear model. Journal of Experimental Child Psychology,99(1), 1–17, doi: 10.1016/j.jecp.2007.08.006.

Laski, E. V., & Yu, Q. Y. (2014). Number line estimation and mental addition: Examining the potential roles of language and education.Journal of Experimental Child Psychology, 117, 29–44, doi: 10.1016/j.jecp.2013.08.007.

Link, T., Huber, S., Nuerk, H. C., & Moeller, K. (2014). Unbounding the mental number line—New evidence on children’s spatial representation of numbers. Frontiers in Psychology, 4, 1021.

Muthén, L. K., & Muthén, B. O. (2012). Mplus user’s guide (7th ed.). Los Angeles, CA: Muthén & Muthén.

Opfer, J. E., Thompson, C. A., & Kim, D. (2016). Free versus anchored numerical estimation: A unified approach. Cognition, 149, 11–17, doi:10.1016/j.cognition.2015.11.015.

Ramani, G. B., & Siegler, R. S. (2008). Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Development, 79(2), 375–394, doi:10.1111/j.1467-8624.2007.01131.x.

Sarama, J., & Clements, D. H. (2009). Early childhood mathematics education research: Learning trajectories for young children. New York: Routledge.

Schneider, M., Grabner, R. H., & Paetsch, J. (2009). Mental number line,number line estimation, and mathematical achievement: Their interrelations in grades 5 and 6. Journal of Educational Psychology,101(2), 359–372, doi: 10.1037/a0013840.

Siegler, R. S., & Booth, J. L. (2004). Development of numerical estimation in young children. Child Development, 75(2), 428–444, doi: 10.1111/cdev.2004.75.issue-2.

Siegler, R. S., & Mu, Y. (2008). Chinese children excel on novel mathematics problems even before elementary school. Psychological Science, 19(8), 759–763, doi: 10.1111/j.1467-9280.2008.02153.x.

Siegler, R. S., & Opfer, J. E. (2003). The development of numerical estimation: Evidence for multiple representations of numerical quantity. Psychological Science, 14(3), 237–250, doi: 10.1111/1467-9280.02438.

Siegler, R. S., & Ramani, G. B. (2008). Playing linear numerical board games promotes low-income children’s numerical development.Developmental Science, 11(5), 655–661, doi: 10.1111/desc.2008.11.issue-5.

Simms, V., Clayton, S., Cragg, L., Gilmore, C., & Johnson, S. (2016).Explaining the relationship between number line estimation and mathematical achievement: The role of visuomotor integration and visuospatial skills. Journal of Experimental Child Psychology, 145,22–33, doi: 10.1016/j.jecp.2015.12.004.

Simms, V., Muldoon, K., & Towse, J. (2013). Plane thinking: Mental representations in number line estimation as a function of orientation,scale, and counting proficiency. Journal of Experimental Child Psychology, 115(3), 468–480, doi: 10.1016/j.jecp.2013.03.011.

Slusser, E. B., Santiago, R. T., & Barth, H. C. (2013). Developmental change in numerical estimation. Journal of Experimental Psychology:General, 142(1), 193–208, doi: 10.1037/a0028560.

Xu, X. H., Chen, C. S., Pan, M. M., & Li, N. (2013). Development of numerical estimation in Chinese preschool children. Journal of Experimental Child Psychology, 116(2), 351–366, doi: 10.1016/j.jecp.2013.06.009.