海港口浮碼頭中固定樁墩振動實測與數值計算分析

丁俊凱 李強 臧傳海

【摘 要】 為更好地研究港口浮碼頭中橋臺墩的位移響應、動力響應特性和振動產生的原因，采用非線性有限元分析軟件Abaqus進行二維數值仿真模擬，并比較實測位移數據得到理論位移曲線。最后與現場工程固定樁墩結構的實測位移曲線進行擬合對比分析，顯示模擬結果與實際工程狀況符合較好，表明鋼引橋的推動力和波浪的動力作用是造成樁墩振動的主要原因，對解決相關工程結構施工安全問題具有實際意義。

【關鍵詞】 固定樁墩;鋼引橋;波浪力;動力響應

0 引 言

港口浮碼頭是由浮躉船、固定樁墩、鋼引橋、錨鏈和一些支撐體系構成的建筑物。

船舶在靠離碼頭時，船體會對浮碼頭承臺樁體產生碰撞、擠壓和摩擦，加上近海波浪力、風力環境的共同作用，對浮碼頭穩定性的要求也越來越高。浮碼頭運營過程中的受力因素較為復雜，需要建立物理模型進行研究。本文基于有限元軟件建立擴展D-P本構關系二維模型模擬浮碼頭中固定樁墩，研究浮碼頭樁―土相互作用、結構耦合振動、信號處理和動力響應分析等方面內容。

本文基于MATLAB編程處理振動加速度信號，結合某碼頭工程，對實際工程中存在的浮碼頭振動問題進行現場測試與分析，認為在復雜環境條件下引起浮碼頭固定樁墩振動的原因是浮躉船在波浪、風等自然條件作用下造成的鋼引橋振動和波浪力直接作用于固定樁墩而引起的結構振動。為驗證這一假設，測試了結構和鋼引橋振動，根據測試結果分析了結構的雙自由度方向振動位移變化，使用Abaqus數值模擬建立了二維樁墩模型，計算得出數據曲線（樁墩的位移振動曲線），并與現場測試數據曲線進行對比。測試結果驗證了這一假設。

1 碼頭工程概況與現場測試

1.1 碼頭工程概況

某海港碼頭擴建工程是在舊固定樁墩外側新修建一段橋臺墩（見圖1，x軸為順岸水平方向，y軸為垂岸水平方向，z軸為豎直方向）。橋臺墩在順岸兩邊與鋼引橋通過兩個部件直接連接，浮躉船與鋼引橋之間有鋼吊架和鋼梁，用側樁柱和錨鏈固定浮躉船。橋臺墩尺寸為14 m 1.8 m，由9根（3）的直徑為0.8 m的管樁組成，樁與樁距離為5 m。鋼引橋使用21 m?m的鋼管傾斜放置，斜率是1︰7。單座鋼引橋質量約19.28 t。

1.2 現場測試

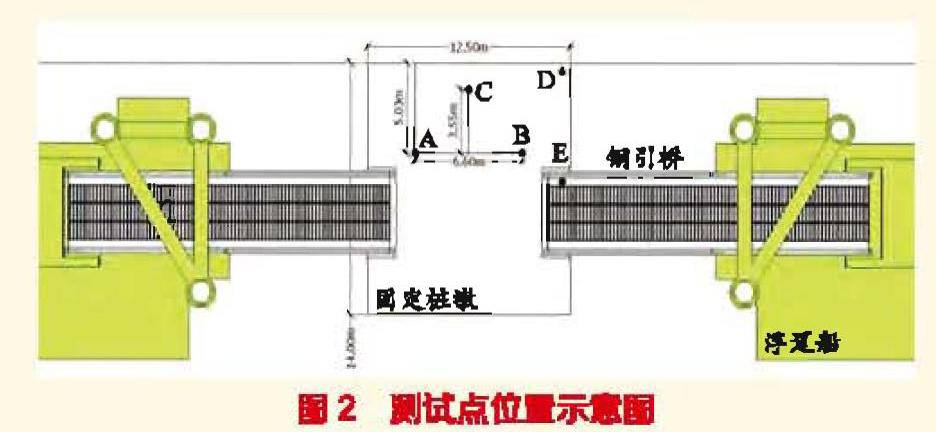
現場測試使用KD1100LC儀器測量，分為3組。測試點位置見圖2，分別為A、B、C，B、C、D，D、E等3組測試點，前兩組測試點在固定樁墩上，第三組測試點則在固定樁墩和鋼引橋上。所有的測試點均測量豎直、順岸、垂岸等3個方向的數值。

1.3 測試數據與分析

使用MATLAB軟件編寫頻率積分程序，繪制豎直、順岸、垂岸等3個自由度方向實測位移曲線，分析經頻域積分處理的固定樁墩豎直方向、垂岸方向及順岸方向的實測位移曲線和鋼引橋豎直方向、垂岸方向及順岸方向的實測位移曲線，得出以下結論：

（1）固定樁墩豎直方向最大位移約為0.8 mm，垂岸方向最大位移為2 mm，順岸方向最大位移為8 mm。

（2）鋼引橋豎直方向最大位移約2 mm，垂岸方向最大位移為10 mm，順岸方向最大位移為10 mm。

（3）無論哪個方向，鋼引橋的振動幅度都要大于固定樁墩的振動幅度。鋼引橋和固定樁墩在順岸和垂岸兩個水平方向的位移都比豎直方向大得多，與實測情況基本吻合。

2 浮碼頭中固定樁墩有限元分析

2.1 平臺模型

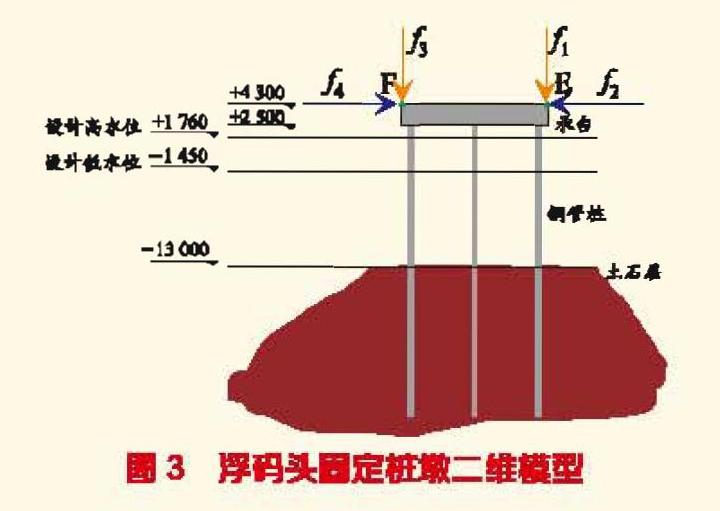
浮碼頭固定樁墩由橋臺墩、管樁和土體組成（見圖3）。

圖3中，E點、F點為橋臺墩與鋼引橋的接觸點，鋼引橋對固定樁墩的作用由鋼引橋自身的重力和鋼引橋振動力共同引起。分別在E點、F點施加同向豎直方向力f1、f3，逆向水平方向施加力f2、f4。若m為鋼橋對點E、F點施加的自身質量，a為模擬數據加速度或者現場實測數據加速度，則f=ma。

2.2 簡化模型的剛度等效

使用二維模型進行計算，會因為維度原因產生誤差，因此要將二維模型和三維模型在水平方向上的剛度進行等效。

2.3 實測與模擬結果

由于模型只對水平方向進行等效，沒有對豎直方向進行等效，因此只對水平方向模擬效果進行分析，而不考慮豎直方向數據。

2.3.1 模擬信號計算結果

在圖3 E點、F點處加集中力，得到模擬信號加速度曲線。通過數學物理方法，考察E點、F點相位變化，計算兩點之間的相位差，從而模擬現場的振動時間差。假設E點、F點初始時間t0為0.10 s、0.20 s、0.30 s、0.40 s、0.50 s、0.60 s，將這兩點的曲線導入軟件進行計算，得出兩點在水平方向位移的結果，見圖4、圖5：

由圖4和圖5可知，E點和F點兩點在水平方向上初始時間（相位差）變大，豎直方向的位移值也在不斷變化。當t0為0.2 s時，相位差達到最大值，即振幅最大，相位差的描述可以簡化為在E、F兩點水平方向加同方向和同大小的作用力f，即f2=f4，這時在水平方向達到振幅的峰值;當t0為0.4 s時，相位差最小，即振幅最小，相位差的描述可以簡化為在E、F兩點水平方向加反方向同大小的作用力f，即f2=-f4，這時在水平方向上達到振幅的谷值。振幅的數值在兩個相位差之間變化，存在極值。由圖3、圖4可以發現振動幅值周期與水平和豎直加速度信號的施加有一定的關系。

2.3.2 實測信號計算與橫向穩定性分析

實際工程中的振幅受到多種因素影響，情況較為復雜。可以先考慮模擬單一波浪力作用因素下E點、F點的二維模型水平方向位移，見圖6。在以上數據基礎上，經過處理，提取鋼引橋測試點同一10 s時段內的加速度數據（見圖7），相當于在兩點施加集中力，將現場實測數據導入數值模擬軟件。考慮承臺兩邊加速度相位變化因素，用同向和反向加速度模擬現實中相位差變化引起的振動幅值變化。

E點和F點在水平方向上的加速度為a2、a4，豎直方向上的加速度為a1、a3。E點、F點的同向加速度在水平和豎直方向上的加速度一致，水平方向相反即a2=-a4，豎直方向相同即a1=a3，結果見圖8，可見其振動波形與波浪力作用下的振型相同，說明E點、F點的水平集中荷載處于同向加速度的情況下會互相抵消，耦合振動為最小值。

E點、F點的反向加速度在水平方向上相同即f2=f4，在豎直方向上相反即f1=-f3，結果見圖9;E點、F點振動波形與圖7情形相比，變化較大，說明E點、F點的水平集中荷載處于反向加速度的情況下振動更加明顯，耦合振動為最大值。

結合圖8、圖9，模擬固定樁墩的二維模型的振動，得到的最大振幅范圍為 6～6 mm。固定樁墩順岸方向實測位移信號見圖10，位移信號曲線比較接近反向加速度的模擬曲線。從圖10可知，由鋼引橋的推動力所引起的位移變化大約是由波浪力引起的位移變化的10倍，可以得出現實中鋼引橋對固定樁墩造成的作用明顯大于波浪力對固定樁墩造成的作用的結論。

2.4 結 論

通過對固定樁墩實測位移和二維模擬位移進行擬合對比分析，可以得出以下結論：

二維模擬固定樁墩位移在水平方向上的模擬結果與實測結果較為接近，而在豎直方向的模擬結果比實測結果小，原因是二維模型在豎直方向沒有對進行剛度等效。

本文所做的有限元模型分析中，固定樁墩的振動主要由兩個因素引起，鋼引橋的振動作用和波浪力的推動作用。其中鋼引橋的振動是樁墩振動的主要原因，模擬計算結果與實測振動信號基本一致，符合實際情況。

波浪對港口浮碼頭建筑物的作用是波浪力、風力等自然因素與固定樁墩、鋼引橋、浮躉船等結構共同互動作用的結果，需要通過建立物理、幾何模型進行分析研究。通過對某港口浮碼頭設計方案的振動作用的物理、幾何模擬，表明當處于極端天氣下，波浪對港口浮碼頭的推動作用更加明顯，對于港口浮碼頭固定樁墩的設計和施工提出了更高的要求。

3 結 語

本文研究了港口浮碼頭在復雜環境下波浪力作用下鋼引橋共振和固定樁墩自振的耦合振動問題，并建立二維數值模型對橋臺墩的剛度數據等效處理后利用有限元法進行二維數值模擬分析，將實測加速度信號頻域積分位移數值結果，與數值模擬位移數值結果進行擬合對比，分析影響浮碼頭結構中固定樁墩的雙自由度振動的因素，得出以下結論：港口浮碼頭中固定樁墩的振動的主要因素是鋼引橋的推動力和波浪的動力作用。