大型集裝箱船快速波激響應分析

林 源，馬 寧，顧解忡

（1.上海交通大學 海洋工程國家重點實驗室，上海200240；2.高新船舶與深海開發裝備協同創新中心，上海200240）

0 引言

隨著全球經濟逐漸一體化，為實現航運的規模效應，集裝箱船的大型化日益加劇。集裝箱船尺度的增加，相應地也會帶來甲板大開口的現象，隨之帶來船體梁固有頻率下降，而航速的提升會增高波浪遭遇頻率，從而會引起船體的共振或強迫振動，將影響船舶的使用壽命。所以在大型集裝箱船的設計制造過程中，水彈性響應分析（如：波激振動）應當被重視。

目前有關船舶水彈性理論已有較為全面的發展。最為經典的水彈性理論就是Bishop 和Price[1]提出的二維理論，然而其忽略流體運動沿船長方向的相互干擾，并未能計及船體首部和尾部的三維效應[2]。接下來Wu[3]，Price 等[4]提出三維水彈性理論，是將三維耐波性與三維結構動力學相結合，但是三維理論需要大量的船體網格。

針對在工程上的快速水彈性預報，三維水彈性理論需要建立大量船體網格，工作量較大。因而簡化網格對于數值計算是必然的，Golberg[5]和Fairweather 等[6]證明了MFS（The method of fundamental solutions）作為一種無網格方法在水動力計算上的優越性，但現階段MFS 方法尚未用于水彈性響應的求解。而且有關的三維有限元與二維耐波性混合模型研究較少，Wang 等[7]將其應用到浮體結構中，但運用到船舶響應求解極少。本文提出一種混合水彈性模型，利用三維有限元方法預報船舶的固有模態，再基于MFS 方法的STF 切片理論[8-9]，進行固有模態下的無網格船體廣義流體力計算，最后根據模態疊加法求解船舶在波浪作用下的波激振動分析。為驗證本方法的計算精度，采用Bernoulli 梁垂向振動模態振型的解析解和水動力軟件HydroSTAR 的數值計算結果進行驗證。

1 船體固有模態預報及波激振動

根據船舶水彈性統一理論，得到船舶在波浪作用下振動的響應方程

其中：a，b 和c 分別表示船體廣義的結構質量、阻尼、剛度矩陣，是N×N 對角矩陣，每個矩陣分別由矩陣系數arr，brr和crr組成，通過結構模態分析獲得。流體廣義質量、阻尼、剛度矩陣分別由A、B 和C 表示，由矩陣系數Ars，Brs和Crs構成，并通過基于MFS 方法的STF 切片方法進行求解。pa和F 分別表示為主坐標和廣義干擾力矩陣。ωe為遭遇頻率。

1.1 模態分析

1.1.1 干模態分析

干模態法是先把結構系統與流體分開，求出真空中結構的固有頻率和固有模態，即干模態[10]。根據實際需要進行模態分離，使自由度數目減少。基于干模態坐標變換下，再進行考慮流體的作用。

根據動力平衡方程有

其中：M、C、K 分別為系統的質量矩陣、阻尼矩陣和剛度矩陣，F（t）為載荷向量，、、r 分別為節點的加速度、速度和位移向量。

真空中結構無阻尼自由振動方程如方程（3）所示，可通過求解得到相應的固有頻率和固有模態。

假設系統做簡諧運動，即為

其中：ω 為頻率，A 為振幅向量，將方程（4）代入方程（3）可得：

若使得方程（5）有非零解，A 不全為零，則有特征方程如下，解此方程得到的響應的特征值和特征向量，即為相應船體干模態的固有頻率ω 和固有振型。

MSC.Patran&Nastran 軟件[11]利用其經驗公式，已給出計算結果精度極高的方法。通過模態分析（Modal analysis），得到固有模態頻率ω 和固有模態振型，并導出振型歸一化的模態質量陣a 和模態剛度陣c。對于結構的廣義阻尼陣b 的相關計算可以按下列方程[10]進行計算，其中

其中：v 為阻尼系數，ωr為r 階模態下的固有頻率，arr為r 階模態廣義質量。小阻尼情況下，對數衰減率為δ≈2πv。一般情況下，其經驗公式如（8）式所示，從而可得到相應的阻尼系數。

1.1.2 濕模態分析

船體的附連水振動質量在MSC.Patran&Nastran 內是通過定義有限元模型濕表面單元號碼和船舶的吃水來自動實現其計算，其理論是用Helmholtz 方法即源匯法（也叫邊界元法）解流體運動的拉普拉斯方程。濕模態是計及周圍水動力影響的結構系統的無阻尼自由振動模態，可通過有限元軟件中設置相關的參數[11]求解濕模態。

1.2 廣義流體作用力

對于有航速的船體廣義流體質量、阻尼和剛度矩陣元素[1]如下所示：

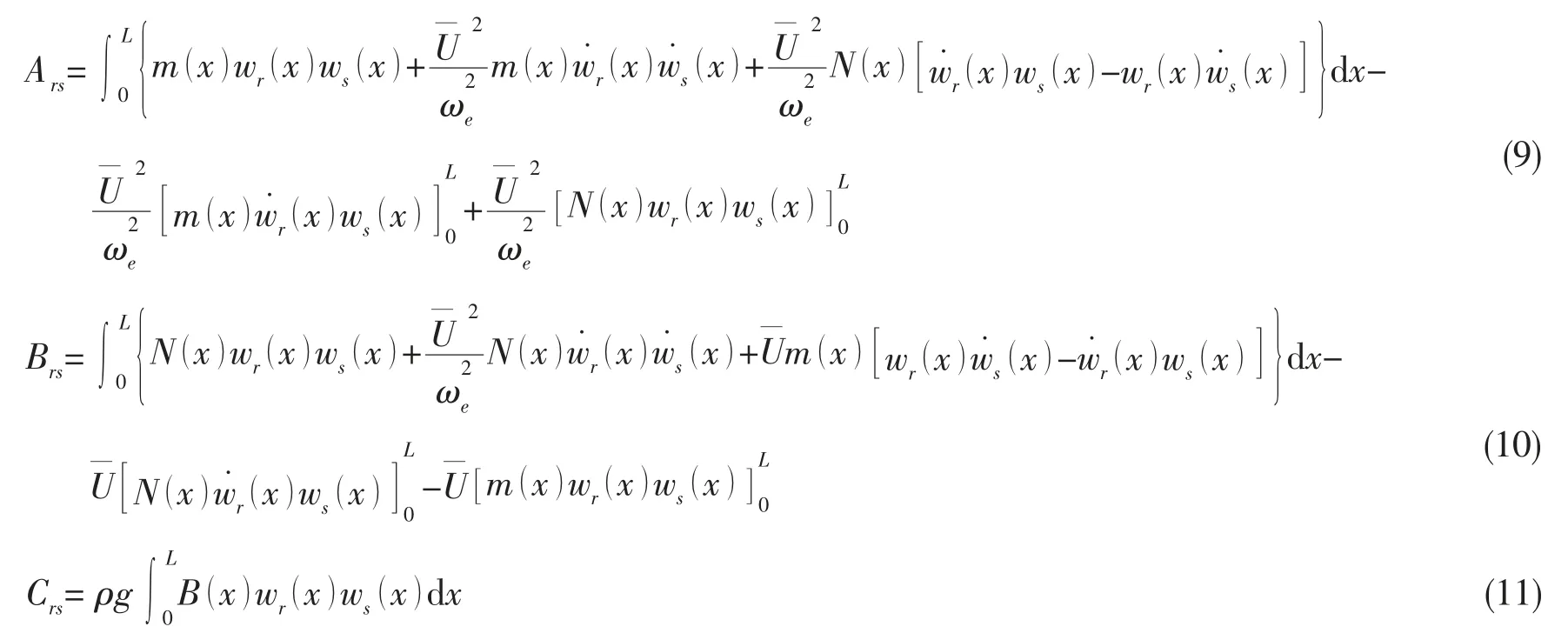
其中：m（x），N（x），B（x）分別為單位船體上的附加質量、流體阻尼系數和微片寬度。對于廣義流體質量、阻尼和剛度矩陣元素的積分，將Feng 等人[9]利用MFS 無網格方法求解船體水動力系數的方法，應用到基于固有模態下的廣義流體作用力系數的求解。

1.3 波激響應

經過上述計算，可以得到船體的廣義質量陣a、阻尼陣b 和剛度陣c，及流體廣義質量陣A、阻尼陣B、剛度矩陣C 和波浪激勵力陣F，便可列出船體的波激振動模態分析方程[10]，即得到相應的主坐標Pa，從而可以求得船體在波浪作用下垂直彎曲振動的動位移w（x，t）、動彎矩M（x，t）和動切力V（x，t）等動力響應。

2 模型精度驗證

為驗證計算模型的精度，本文通過三維有限元固有模態計算結果與Bernoulli 梁的解析解[10]（如方程（15）所示）對比，從而對固有模態的求解精度進行了驗證。

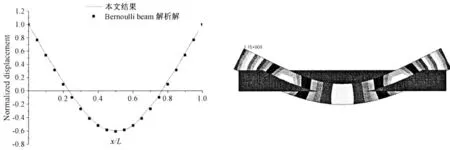
圖1 Bernoulli 梁1 階模態的三維有限元計算結果與梁解析解對比Fig.1 The comparisons between the first order model shapes of Bernoulli beam by 3D FEM and the analytical solution

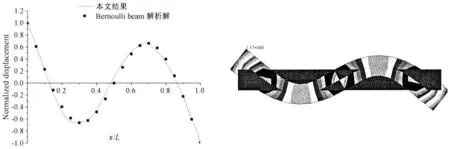
圖2 Bernoulli 梁2 階模態的三維有限元計算結果與梁解析解對比Fig.2 The comparisons between the second order model shapes of Bernoulli beam by 3D FEM and the analytical solution

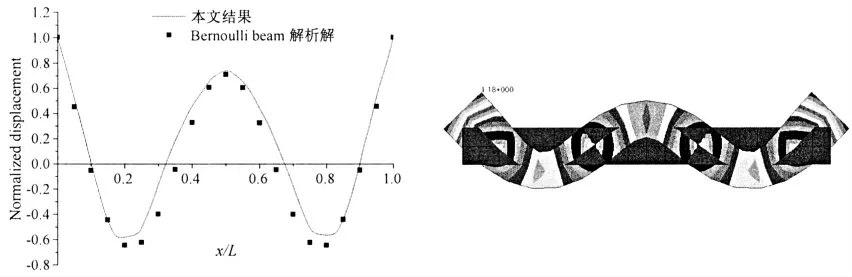
圖3 Bernoulli 梁3 階模態的三維有限元計算結果與梁解析解對比Fig.3 The comparisons between the third order model shapes of Bernoulli beam by 3D FEM and the analytical solution

其中：kr為特征值，其取值滿足如下特征方程：cos krL·cosh krL=1。關于三維有限元結果和Bernoulli 梁的解析解，這里均采用了將船尾處的位移歸一化為單位1，方便對比分析。根據剖面上的點位移轉角和剖面存在一定的幾何關系，將三維Bernoulli 梁模型模態分析后剖面的節點的位移回歸得到歸一化的振型圖。圖1 至圖3 分別給出了1 至3 階固有模態計算結果和解析解的對比。其中1 階和2 階模態計算結果能夠與解析解達到90%以上的重合程度。從而證明應用三維有限元方法進行波激振動的固有模態分析，較遷移矩陣隨迭代而逐步疊加誤差，能為進一步基于模態振型下的流體水動力系數求解提供更高的精度。

通過ANSYS 軟件對于三維有限元模態分析結果進行交叉的計算驗證，通過表1 可看出，MSC.Patran&Nastran計算結果有保證。

表1 MSC.Patran&Nastran 與ANSYS 計算固有模態對比分析Tab.1 Comparisons on modal analysis results between MSC.Patran &Nastran and ANSYS

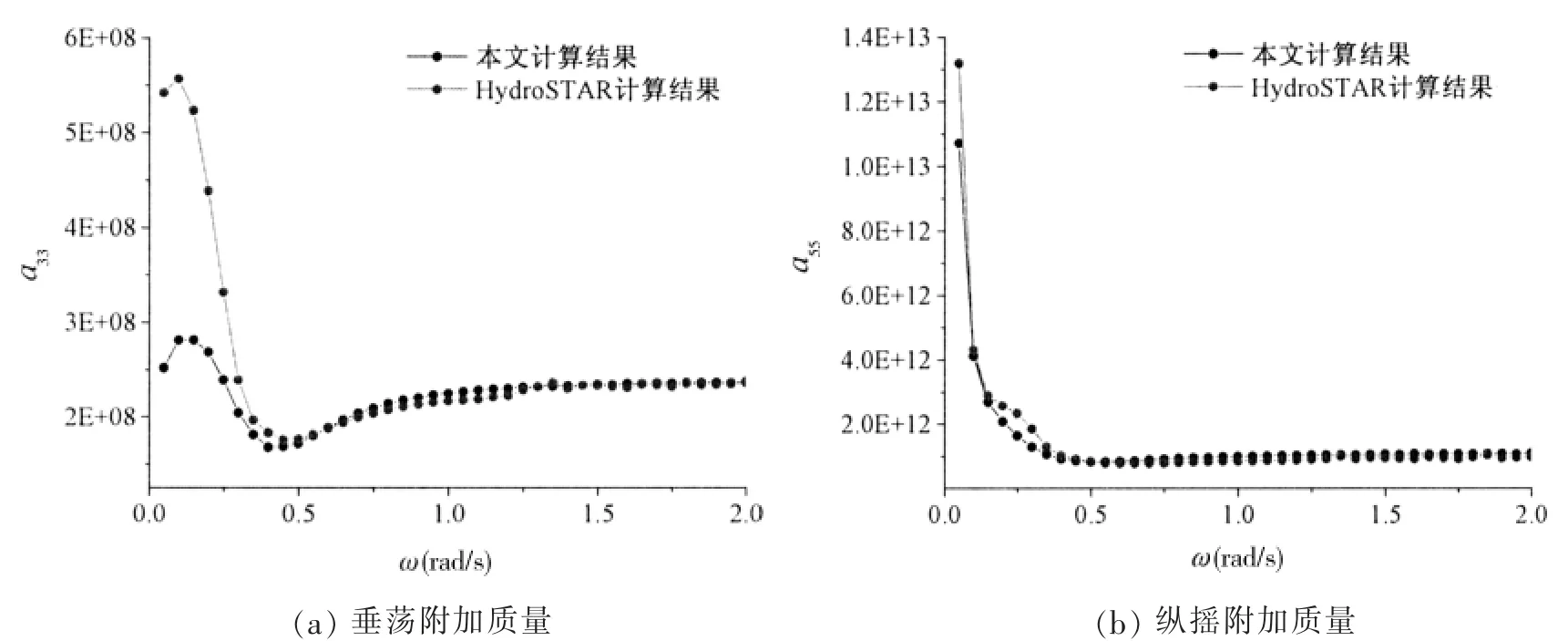
圖4 大型集裝箱船垂蕩和縱搖附加質量曲線Fig.4 Heave and pitch added mass of very large container ship

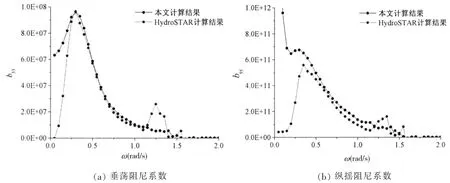
圖5 大型集裝箱船垂蕩和縱搖阻尼系數曲線Fig.5 Heave and pitch damping of very large container ship

本文為驗證模型耐波性部分計算的正確性，計算了迎浪狀態下、100%服務航速時大型集裝箱船的垂蕩和縱搖的附加質量、附加阻尼和激勵力，與商業軟件HydroSTAR 計算的結果對比分析，如圖4 至圖6所示。在中高頻波浪下，本文的計算結果精度可以滿足，對于由于切片法本身的弊端，低頻情況下的精度上仍需改善。但是總體上的誤差在15%以內，并且由于低頻部分對于波激振動趨勢的展示影響較小，故而可以滿足工程需求。

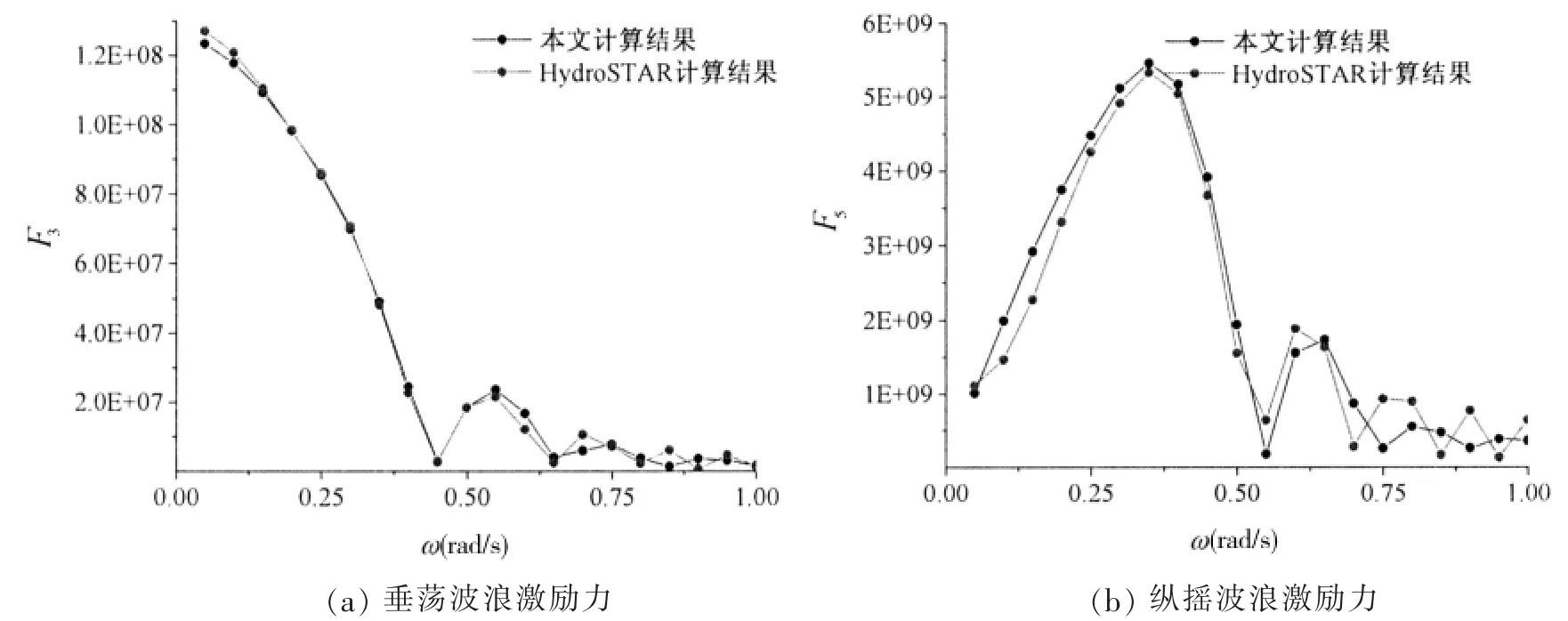
圖6 大型集裝箱船垂蕩和縱搖波浪激勵力曲線Fig.6 Heave and pitch excitation of very large container ship

3 大型集裝箱船波激振動分析

對大型集裝箱船的有限元分析，是通過MSC.Patran &Nastran 軟件，得到了各階固有干模態的固有振型及相應的廣義質量、廣義剛度，并通過經驗公式得到相應的廣義阻尼，匯總成表，如表2所示。

表2 大型集裝箱船的干濕模態預報結果及結構廣義質量、剛度、阻尼值Tab.2 Dry and wet mode prediction and the generalized mass,damping and stiffness

根據剖面上的點位移轉角和剖面存在一定的幾何關系，將三維集裝箱船模型模態分析后剖面的節點的位移回歸得到歸一化的振型圖。其中大型集裝箱船的第1 階至第3 階對稱振動的固有振型圖，如圖7 至圖9所示，考慮到大型集裝箱船的寬大型、大甲板開口復雜性，采用三維有限元方法對船舶進行模態分析，計算結果與船體梁的遷移矩陣模態分析相比，精準度較高。

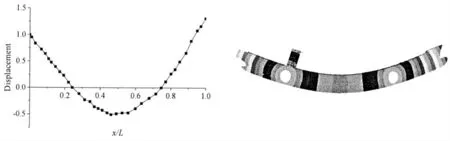
圖7 某大型集裝箱船1 階垂向模態振型圖預報Fig.7 The predicted results on first order mode shape of very large container ship

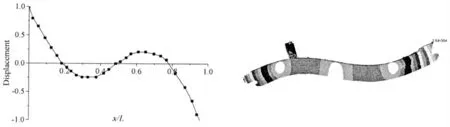
圖8 某大型集裝箱船2 階垂向模態振型圖預報Fig.8 The predicted results on second order mode shape of very large container ship

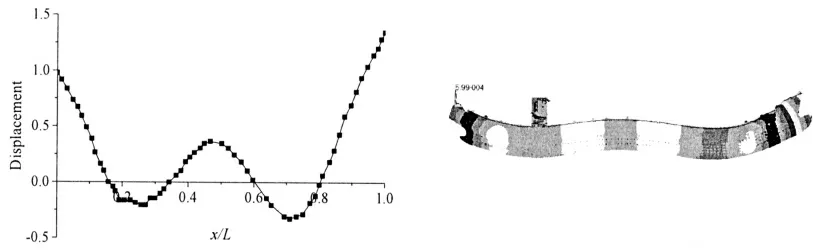
圖9 某大型集裝箱船3 階垂向模態振型圖預報Fig.9 The predicted results on third order mode shape of very large container ship

通過上述模態分析，將回歸后的歸一化振型運用到廣義流體作用力的計算，從而進一步可以求解相應的波激對稱振動方程。為考慮航速對于主坐標的影響，采用迎浪下100%服務航速和50%服務航速的數值計算，可以通過圖10 看到對稱響應主坐標幅值隨船長與波長之比L/λ 變化趨勢。對于第1階和第2 階垂直彎曲模態，其主坐標變化趨勢相同，且第1 階主坐標最大幅值大于第2 階主坐標最大幅值，具有船舶波激響應的一般趨勢。當航速增大時，主坐標的數值相應也有一定程度的增大，并且第一個峰值皆出現在L/λ=1 處，證明了計算結果的準確性。隨著遭遇頻率的增加，在L/λ≈8.75 和18.68 時產生第二個和第三個峰值。根據波長與波頻關系式有L/λ=Lω2/2πg，遭遇頻率ωe=ω-ω2Ucos β/g，可以求出對應L/λ≈8.75、18.68 時，遭遇頻率為2.353 rad/s 和4.147 rad/s，說明本方法的可行性。而且較三維水彈性方法，采用無網格MFS 的STF 法求解流體水動力系數可簡化網格，降低計算難度和節省時間。

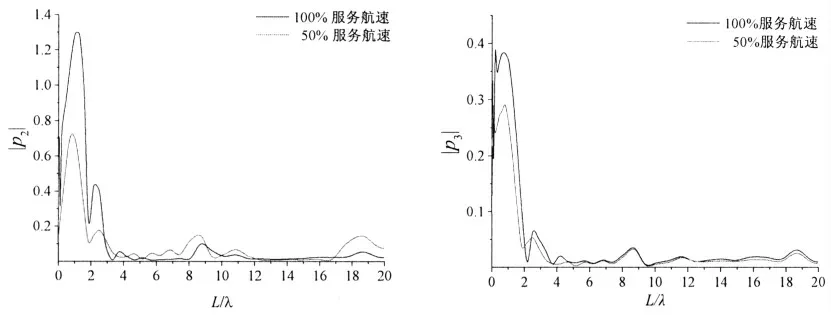
圖10 不同航速迎浪航行時的主坐標和變化曲線（左圖為，右圖為）Fig.10 The third and fourth principal mode curves of various speeds in the heading sea

4 結論

本文以集裝箱船為目標船型，提出了三維有限元結構分析與二維耐波性分析相結合的水彈性預報方法，并基于該方法對某大型集裝箱船的波激響應進行了分析：

（1）本文方法較目前的三維水彈性分析大幅簡化了網格劃分、提高了計算效率；且與二維水彈性方法相比，在結構分析時能夠提高精度，具有較好的工程實用價值；

（2）本文通過MSC.Patran &Nastran 軟件模態分析得到的固有振型方法，經過梁模型驗證，平均精度在90%以上；計算的固有頻率，與ANSYS 軟件計算結果相比，精度有保證；

（3）本文基于STF 切片理論計算的廣義流體相關系數，忽略船體變形的剛體運動，與三維HydroSTAR軟件對比，精度在85%以上，具有工程實用價值，但在未來階段仍需改進低頻部分的精度問題；

（4）基于本文模型得到的波激對稱響應，符合船舶水彈性相關特性，得到共振的遭遇頻率分別為2.353 rad/s 和4.147 rad/s。