水深對機槍密封式膛口流場影響的數值分析

張欣尉，余永剛

（南京理工大學 能源與動力工程學院，南京210094）

0 引言

槍炮水下發射時，水的密度約為空氣密度的800 倍，為保證發射安全性和威力，Stace 等[1]提出了水下密封式發射，即在膛口加裝密封裝置，當彈前空氣壓力達到某一數值時密封裝置打開，隨后彈丸運動出膛。密封式發射時，膛口周圍水介質將對彈丸運動和燃氣射流的擴展產生較大影響，針對水深變化對密封式發射膛口流場影響的研究對于水下槍炮的研究具有一定理論意義和工程價值。

膛口流場對彈丸運動以及周圍環境均具有重要的影響作用，對于槍炮在空氣中發射所形成的膛口流場，國內外專家學者開展了大量研究工作。Klingenberg 等[2]對7.62 mm 步槍膛口焰及溫度進行了測量。Jiang 等[3]針對馬赫數為3.0 的高速射彈的膛口流場進行了數值模擬，捕捉并詳細分析了其波系特征。吳偉等[4]基于無網格算法再現了膛口流場中膛口初始沖擊波、膛口沖擊波、欠膨脹射流波系結構的動力學發展過程。Zhang 等[5]和Florio[6]分別從實驗和數值模擬方面研究了炮口制退器結構對膛口流場的影響。水下密封式膛口流場還涉及到高溫高壓燃氣射流水中擴展，而對于高溫高壓燃氣射流的研究已經十分豐富。Xu 等[7]基于volume of fluid（VOF）多相流模型對水下火箭噴管高速燃氣射流進行了數值模擬。莽珊珊等[8]對充液室邊界形狀對圓形射流擴展的影響進行了實驗和數值研究。唐云龍等[9]采用VOF 模型對水下高速欠膨脹燃氣射流的結構及推力特征進行了研究。Xue 等[10]對雙股燃氣射流在階梯狀充液室內的擴展進行了實驗研究和數值分析，發現直徑增量與孔間距的比值大于0.6 時有利于射流的匯聚和徑向擴展。Zhou 等[11-12]和Hu 等[13]對多股燃氣射流在圓管內的擴展進行了實驗和數值研究，兩者采用不同噴孔結構對水下槍炮氣幕式發射過程中的多股射流協同排水效果進行了對比分析。

目前，對于水下槍炮密封式發射的研究仍較少，劉育平等[14]對水下炮密封式發射的內彈道過程進行了數值計算，發現膛壓升高而初速降低，并捕捉到了膛口內部激波。對水下槍密封式膛口流場的研究更為少見，本文數值模擬了3 種水深條件下的密封式膛口流場，重點討論了水深對密封式膛口流場的影響，對水下密封式發射槍炮的研究具有一定參考意義。

1 數理模型

VOF 多相流模型被廣泛地應用于對水中燃氣射流的研究[8-12]，本文同樣采用該模型對膛口燃氣射流進行數值模擬。

1.1 物理模型

根據水下槍炮密封式發射特點，對12.7 mm 滑膛式機槍水下密封式膛口火藥燃氣流場，采用以下簡化假設：

（1）膛口燃氣射流的擴展看作是一個非穩態過程，近似處理為二維軸對稱問題；采用k-ε 模型模擬流場中氣液湍流作用。

（2）膛口燃氣射流近似處理為可壓縮理想氣體射流，不考慮燃氣射流的組分變化，并忽略其體積力的影響。

（3）不考慮槍口附近水的相變以及空化的影響。

數值計算中多相流模型采用VOF 模型，湍流模型采用標準k-ε 模型。利用PRESTO! 方法對壓力項離散，動量和能量的離散采用一階迎風格式，壓力與速度耦合采用PISO 算法，計算過程中時間步長控制在0.2 μs 以內，以保證計算穩定性。

1.2 數學模型

根據1.1 節物理模型，對燃氣射流建立以下數學模型：

（1）連續性方程

式中：ρq表示密度，q=1，2 分別表示氣、液兩相；α1和α2分別表示氣液各相的體積分數，且α1+α2=1；υ為速度矢量。

（2）動量方程：

式中：氣液混合密度ρ=α2ρ2+（1- α2）ρ1；ρ 為壓強；μ 為粘度系數。

（3）能量方程：

（4）氣體狀態方程：

式中：R 為理想氣體常數，R=8.314 J / (mol·K)。

（5）k-ε 湍流方程：

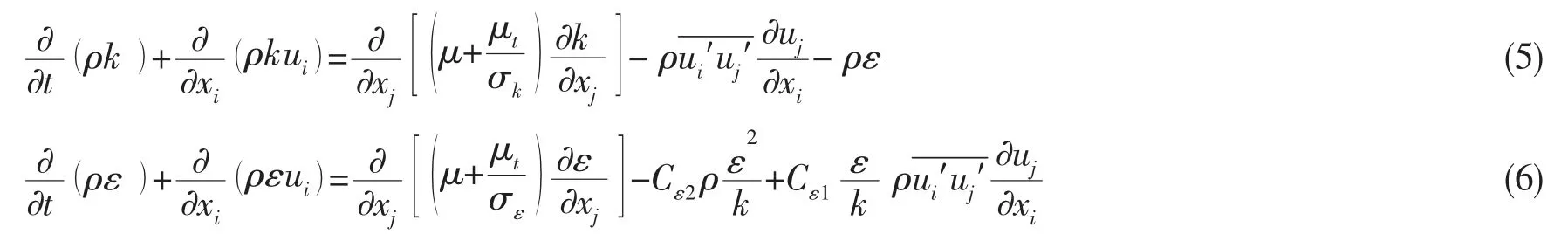
式中：k 和ε 分別為湍動能和耗散率；常數σk=1.0 和σε=1.3 分別為湍動能與耗散率對應的Prandtl 數；μt=Cμk2/ε 為湍流粘性系數，xi和xj為坐標矢量；ui和uj為為速度矢量；i 和j 為自由指標；常數Cε1=1.44、Cε2=1.92 和Cμ=0.08 為經驗系數。

1.3 數理模型的實驗驗證

本研究對文獻[8]中圓形燃氣射流在圓柱形充液室內擴展的實驗進行了數值模擬，圖1 為數值模擬和實驗中射流頭部軸向最大位移與時間的關系對比圖。由圖1可知，數值模擬結果與實驗結果吻合較好，最大誤差僅為2.8%，說明本文所采用的數理模型是可信的。

2 邊界條件與計算模型

針對計算需求，對計算域進行以下劃分：彈后燃燒室、身管和膛口周圍區域。

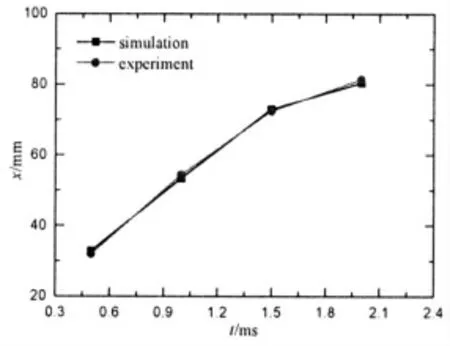
圖1 射流頭部軸向最大位移與時間的關系Fig.1 The relationship between the maximum displacement of the jet head and the time

2.1 網格劃分

本節給出了水下密封式發射計算模型，如圖2所示，其中圖2（a）為計算模型示意圖，圖2（b）為計算域網格示意圖。由圖2（a）顯示，計算分三個區域，Ⅰ區為彈后燃燒室，Ⅱ區為彈前身管內部，Ⅲ區為膛口周圍流場，膛口流場計算區域取長為0.7 m、半徑為0.2 m 的圓柱形區域。由圖2（b）顯示，計算域采用結構化和非結構網格，最小網格尺寸為0.25 mm×0.25 mm，位于Ⅲ區彈丸運動區域，即槍口至出口邊界間長0.5 m、半徑0.006 35 m 的圓柱形區域。在圖2（a）中，O 點為膛口中心，以其為參考零點，P 點坐標為（100 mm，19.05 mm）。

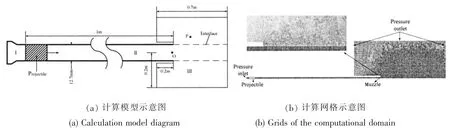
圖2 水下密封式發射計算模型Fig.2 Computational model for underwater sealed launch

2.2 邊界條件

燃燒室設為壓力入口，彈丸定義為運動剛體，膛口流場計算區域外邊界為壓力出口邊界，初始化為環境變量參數，即水深為1 m 時初始壓力為111 325 Pa，水深50 m 時初始壓力為601 325 Pa，水深100 m 時初始壓力為1 101 325 Pa；忽略水深對溫度的影響，即初始溫度均取300 K。

2.3 網格無關性驗證

考慮到動網格的分裂與合并，最小網格尺寸設定為0.25mm×0.25mm，對膛口周圍流場（Ⅲ區）進行不同尺寸網格加密設置，分別得到21.5 萬、17.9 萬和13.4 萬網格數的計算網格。由于圖2（a）中P 點會經歷氣液相態轉變及射流夾斷等復雜變化，故選其進行網格無關性驗證具有一定代表性。以三種網格數下的P 點壓力隨時間變化為參考，如圖3所示。圖3 顯示，與21.5 萬網格數下P 點壓力相比，采用17.9 萬網格數進行計算時平均誤差為4.8%，而采用13.4 萬網格數進行計算的平均誤差達到16.1%，為保證計算精度和計算效率的最優配置，本研究采取17.9 萬網格進行數值計算。

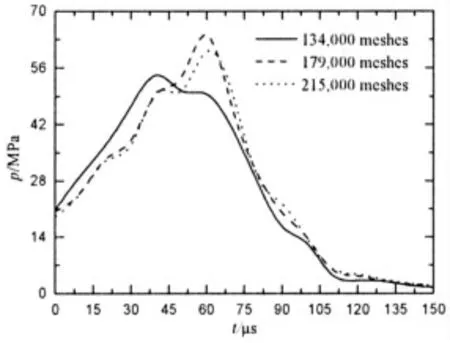
圖3 采用不同網格數計算的參考點壓力-時間對比Fig.3 Pressure-time curves of reference point under different grids

3 結果與討論

通過數值模擬，對滑膛式機槍在不同水深條件下密封式發射的彈道結果和膛口流場特性進行了分析，彈丸口徑為d0=12.7 mm、彈丸長度為l0=50 mm，膛口密封膜片打開條件為內外壓力差Δp=105Pa。

3.1 彈道結果

由計算可知，隨著水深增加，槍口初速降低明顯，最高膛壓略有升高，內彈道參數見表1。同時給出了不同水深條件下彈丸出膛后的膛外行程對比曲線，見圖4，由圖可知，水深越大彈丸運動越慢，且隨著彈丸速度降低，速度衰減將加快。

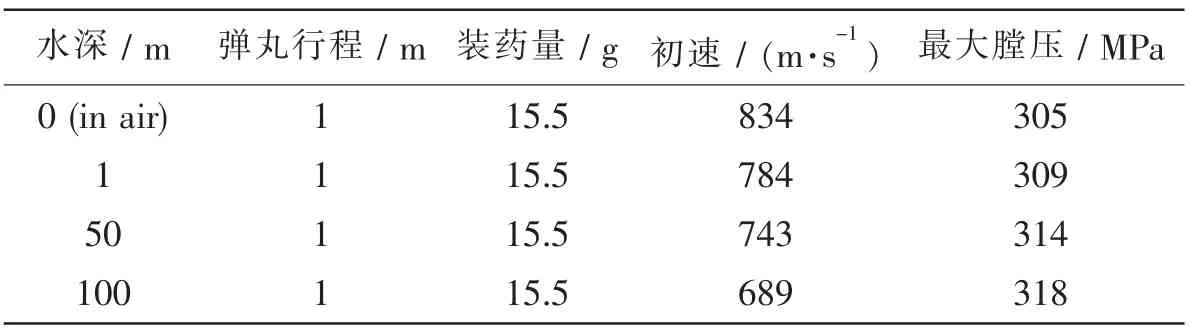
表1 內彈道參數Tab.1 Interior ballistics parameters

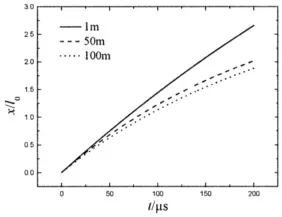
圖4 不同水深下彈丸膛外行程Fig.4 Projectile displacement out of muzzle under different water depths

對彈丸行程隨時間變化特性進行擬合，發現其在不同水深條件下均滿足指數函數規律，即：

x（t）=x0+x1e-t/t1

式中：x（t）為彈丸膛外行程；t 為時間，s；x0，x1和t1為彈丸膛外行程隨時間變化的擬合參數，如表2所示。

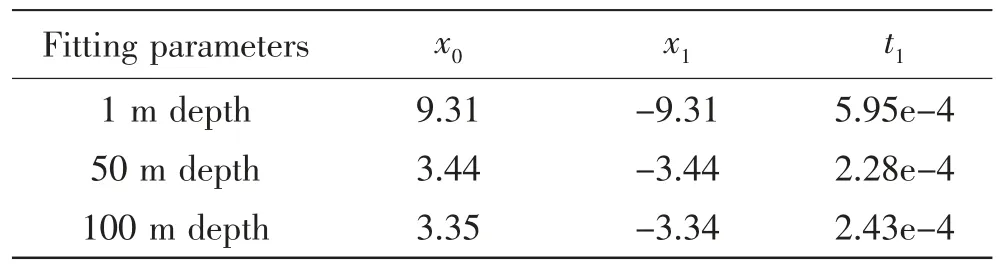
表2 彈丸膛外行程隨時間變化的擬合參數Tab.2 The fitting parameters for the displacementtime curves of the projectile

3.2 膛口流場

通過數值模擬，得到了12.7 mm 機槍水下密封式膛口流場分布情況，圖5-7 分別為1 m、50 m 和100 m 水深條件下的膛口溫度場和速度場分布云圖。

圖5 1 m 水深條件下膛口溫度場和速度場分布Fig.5 Distribution of muzzle temperature and velocity field under 1 m depth condition

由圖5-7 中射流邊界可知，相同時刻，水深越大射流徑向擴展越大，而軸向擴展越小，這是因為水深較大時彈丸初速較低且衰減快，彈丸運動距離較近，不利于燃氣軸向擴展，從而導致燃氣射流徑向擴展明顯。由溫度場與速度場分布可知，水深越大，波系核心區分布區域越小，這是受環境壓力的壓縮作用影響；比較相同時刻燃氣射流速度場分布可知，水深較小時燃氣射流擴展速度更快，這也印證了氣體空腔和波系核心區分布大小規律。3 種水深條件下，燃氣出膛經過膨脹區后被壓縮產生高溫氣團，隨著時間推移，高溫氣團向下游運動，隨后新的高溫氣團產生；在1 m 和50 m 水深條件下，高溫氣團逐漸被壓縮，分布范圍縮小而溫度升高，而100 m 水深條件下的高溫氣團移動較慢，從70 μs 到200 μs，分布區域變化不大；觀察可知，水深越大，高溫氣團向下游移動也越慢，燃氣集聚在離膛口更近的位置。

圖6 50 m 水深條件下膛口溫度場和速度場分布Fig.6 Distribution of muzzle temperature and velocity field under 50 m depth condition

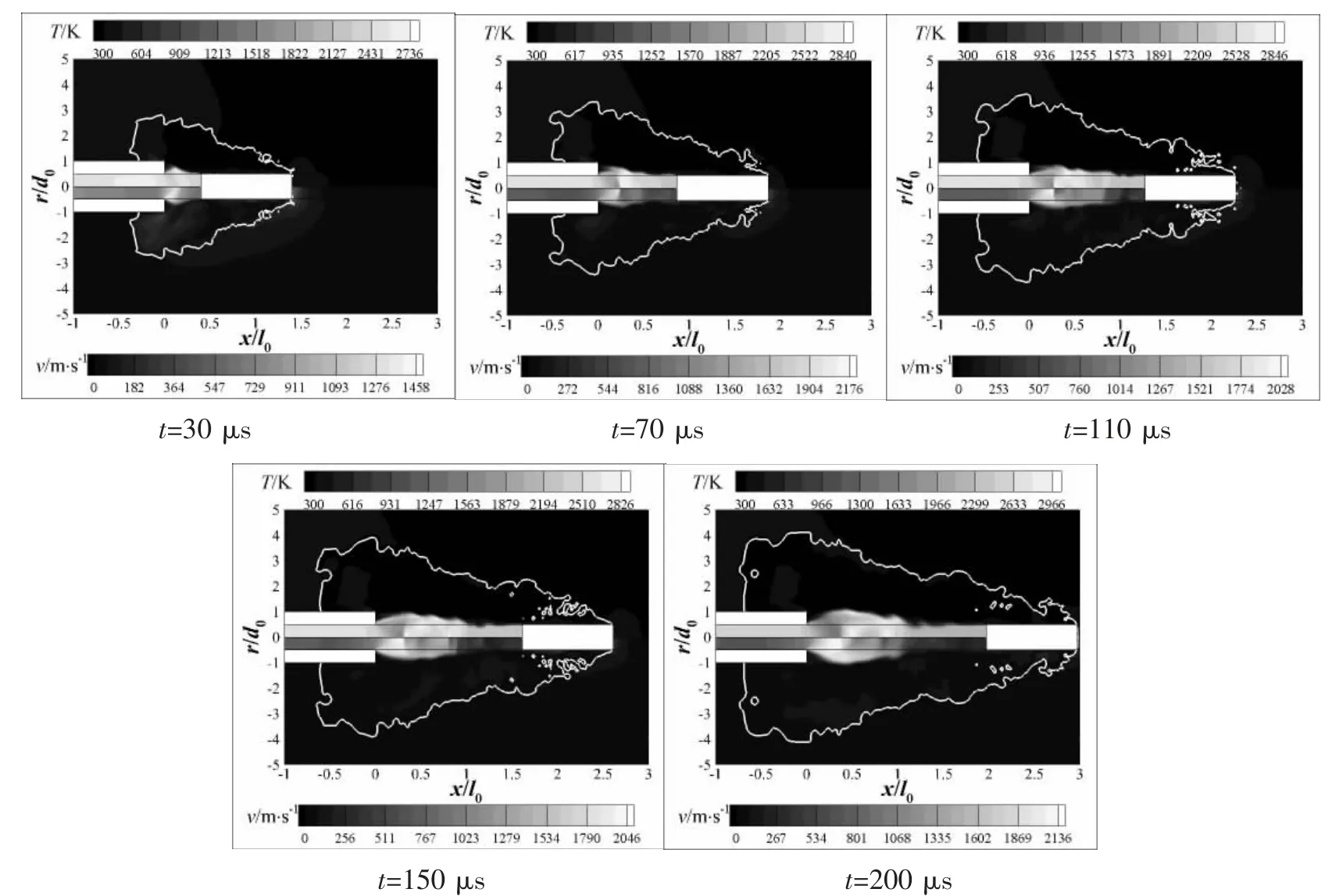
圖7 100 m 水深條件下膛口溫度場和速度場分布Fig.7 Distribution of muzzle temperature and velocity field under 100 m depth condition

同時，由圖5-7 中溫度云圖可以發現，3 種水深條件下最高溫度的出現時刻均比較靠后，出現位置逐漸靠近膛口，說明密封式膛口流場演化及分布具有一定規律性。為了進一步了解流場中溫度分布和馬赫盤位置，圖8給出了3 種水深條件下膛口至彈底中心溫度沿軸向分布曲線。

由圖8 可以發現，3 種水深條件下，馬赫盤結構在70 s 時刻均已形成，但隨著水深增大，馬赫盤位置離膛口越來越近。燃氣射流在膨脹區頭部，即馬赫盤位置達到最低溫度：200 s 時刻，1 m 水深條件下，最低溫度約為900 K；50 m 水深條件下，最低溫度約為1 325 K；100 m 水深條件下，最低溫度超過1 500 K；由此可見，隨著水深增加，燃氣射流膨脹區縮小，馬赫盤位置更靠近膛口，但激波膨脹區內最低溫度卻升高。由圖8 中200 μs 溫度曲線可知，燃氣射流在越過馬赫盤后溫度出現多次波動，1 m水深時溫度出現4 個波動峰值，50 m 水深時溫度出現3 個波動峰值，100 m 水深時溫度出現2 個波動峰值。結合圖5-7 中200 μs 時刻的溫度云圖可以發現，隨著水深增加，彈丸運動距離較近、燃氣射流速度也降低，使得高溫氣團的演變減慢，從而導致燃氣在越過馬赫盤后的壓縮-膨脹次數減少，溫度波動減弱。

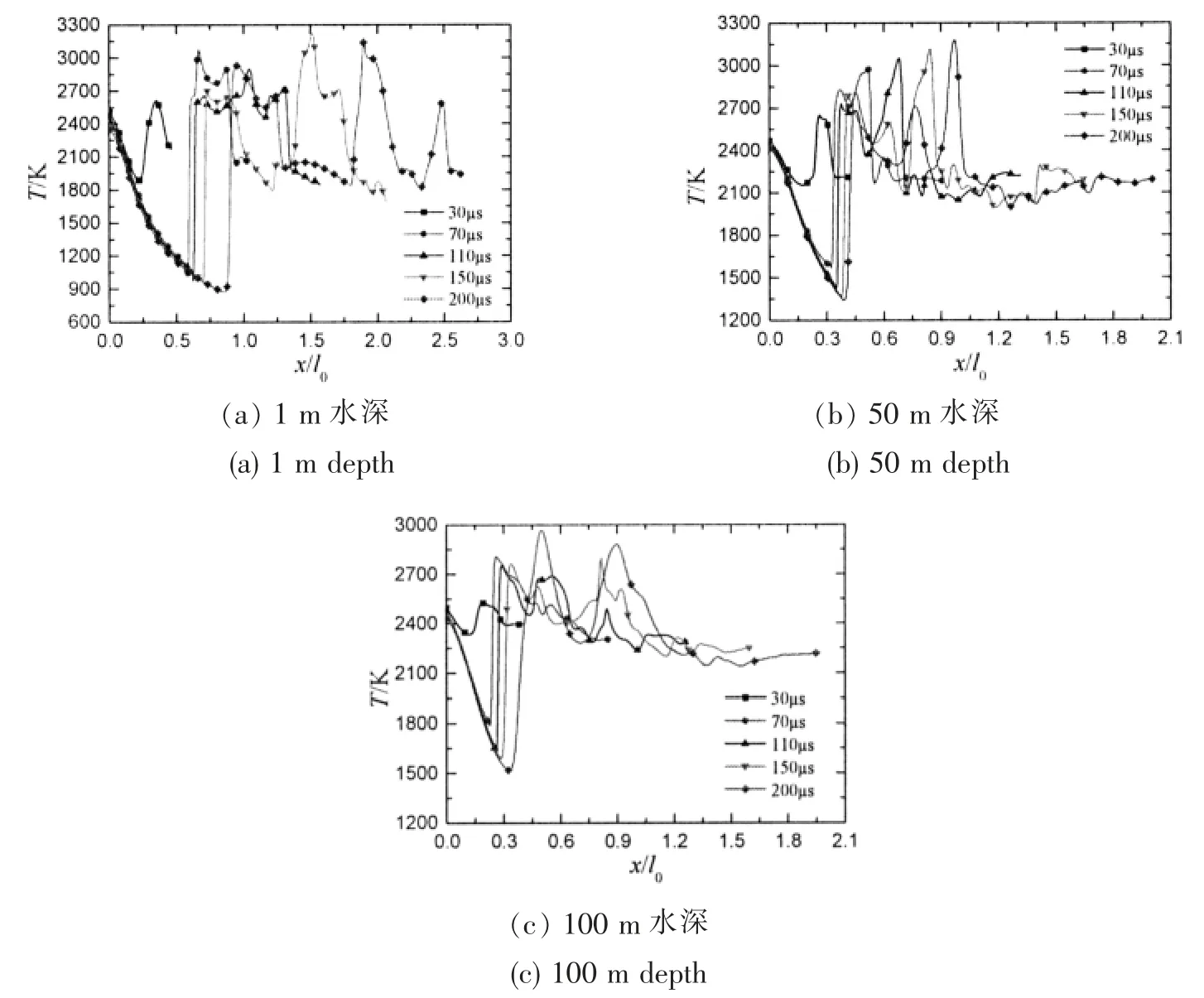
圖8 膛口-彈底中心溫度沿軸向分布Fig.8 Temperature distribution along the axis from muzzle center to projectile base

4 結論

通過對12.7 mm 滑膛式機槍水下密封式發射的數值模擬，發現水深對彈道結果和膛口流場的演變具有一定規律：（1）水深增大，彈丸初速降低，速度衰減隨速度降低加快，射流軸向擴展減緩而徑向擴展加快；（2）不同水深條件下，彈丸膛外行程均滿足指數變化規律；（3）水深增大，燃氣射流激波核心波系區域減小，同時激波膨脹區被壓縮，馬赫盤位置離膛口距離更近；相同時刻，燃氣在馬赫盤位置溫度更高而速度更低；（4）200 μs 時刻，隨著水深增加，燃氣射流在越過馬赫盤后出現壓縮-膨脹次數減少、溫度波動減弱。本文結論對水下槍炮的設計具有一定參考價值。