差動調速的風電機組傳動特性研究
芮曉明 尹文良
華北電力大學能源動力與機械工程學院,北京,102206
0 引言
隨著風電系統產業規模的擴大及其所占電力生產比例的增加,現有變速恒頻并網風力發電技術存在的問題日漸凸顯,主要包括無功功耗大、動態穩定性差、發電機結構復雜等。此外,所需的部分或全功率變頻設備會產生諧波電流而影響發電質量,低電壓穿越能力不足也亟待解決[1-2]。
針對上述問題,一些學者提出可連續變速的風電機組傳動方案[3-11],基于先進的調速傳動與伺服控制技術,構成“帶有發電機前端調速裝置的風電機組”,以實現變速恒頻。IDAN等[3]提出了一種利用兩級行星輪系來實現風電機組恒速運行的方案。針對此方案,REX等[4]提出了包含比例積分控制器和非線性力矩控制器的調速控制方法。以上方案雖然可滿足大部分風電機組的調速需求,但使用多個伺服電機時,成本高,能量消耗大。穆安樂等[5]設計了一種帶有柔性混合驅動環節的風能轉換系統,并給出了伺服調速電機調速幅度、調速深度、調速帶等關鍵參數的計算方法。LIU等[6]基于千瓦級試驗平臺,驗證了混合傳動風電機組的可行性和實用性。RUI等[7-11]利用差動齒輪箱和調速電動機,實現了風電機組恒頻輸出,并對所提機組的傳動原理、性能仿真和可行性驗證實驗等方面展開了研究。
上述研究大多集中在機組概念方案設計、控制策略和可行性驗證等方面,關于風電機組齒輪傳動系統的傳動特性等方面的研究較少,因此,筆者對差動調速的新型風電機組的傳動系統運動學原理、功率流向與關鍵構件轉速的關系以及系統傳動效率進行研究。
1 差動調速風電系統原理
差動調速風電系統構成方案見圖1,主要包括風輪、增速齒輪箱、差動調速系統、同步發電機和電網五大部分。風輪吸收隨機變化的風能,產生隨機變化的轉速和轉矩;在經過增速齒輪箱增速后傳遞給差動輪系行星架,構成系統的主輸入;同時,調速電機產生的轉速和轉矩傳遞給差動輪系齒圈,構成系統調速輸入;差動輪系太陽輪與同步發電機相連。系統利用伺服控制技術,實時調節發電機轉速,以實現變速恒頻。

圖1 差動調速風電系統構成圖Fig.1 Layout of wind turbine with differential speed regulating
由圖1可知,差動輪系是差動調速系統核心部件,需有兩個獨立確定的輸入來確定太陽輪輸出;差動輪系結構見圖2,各主要構件的轉速平衡方程如下:
(1)

圖2 差動輪系結構圖Fig.2 The structure chart of differential gear train
令太陽輪與同步發電機之間的傳動比為1,由傳動方案可得發電機轉速為
ng=(1+k)nC-knR=(1+k)nriCr-knmiRm
(2)
式中,k為差動輪系結構參數;nS、nR、nC、ng、nr、nm分別為太陽輪、齒圈、行星架、發電機、風輪和調速電機的轉速;iCr為行星架與風輪之間的傳動比(增速齒輪箱傳動比);iRm為調速電機與齒圈之間的傳動比;ZR、ZS分別為齒圈和太陽輪的齒數。
對于實際的風電機組,參數k、iCr、iRm的取值與傳動系統實際結構和參數有關,均為固定值。由式(2)可知,當轉速傳感器采集到風輪轉速nr后,將其傳輸到電機控制單元,實時控制調速電機轉速nm,最終可以使得發電機轉速ng恒定,從而發出恒頻電能入網,以實現機組變速恒頻。
2 機組傳動特性分析
2.1 整體功率流向分析
本文采用轉化機構法[12]對行星輪系進行分析。定義轉化機構效率為ηH,IRS=nR/nS為齒圈與太陽輪之間的轉速比。此時差動輪系功率平衡方程滿足:
(3)
在穩定運行狀態下,差動輪系各構件的加速度為0,則得到轉矩平衡關系如下:
TS+TR+TC=0
(4)
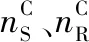
依據式(1)~式(4)可得
(5)
為了更好地研究總體功率流向,結合式(5)定義相對功率系數φRS(齒圈與太陽輪傳遞功率比)、φCS(行星架與太陽輪傳遞功率比)和φRC(齒圈與行星架傳遞功率比)分別為
(6)
式中,ICS為行星架與太陽輪之間的轉速比。
根據相對功率系數φRS、φCS和φRC的定義可知,若φRS>0,則表明齒圈和太陽輪的驅動狀態一致(齒圈和太陽輪同為輸入構件或同為輸出構件),總體功率流經行星架;若φCS>0,則行星架與太陽輪的驅動狀態一致,總體功率流經齒圈;若φRC>0,則齒圈與行星架的驅動狀態一致,總體功率流經太陽輪。基于上述研究,結合式(6)可得到總體功率流向和關鍵構件轉速關系,見表1。表1中,“+”表示相應條件下各參數為正,“-”表示相應條件下各參數為負。對于實際差動輪系,其結構參數與具體機械結構相關,且結構參數為確定的正數,因此,表1只考慮k> 0的情況。

表1 總體功率流向分析(k>0)
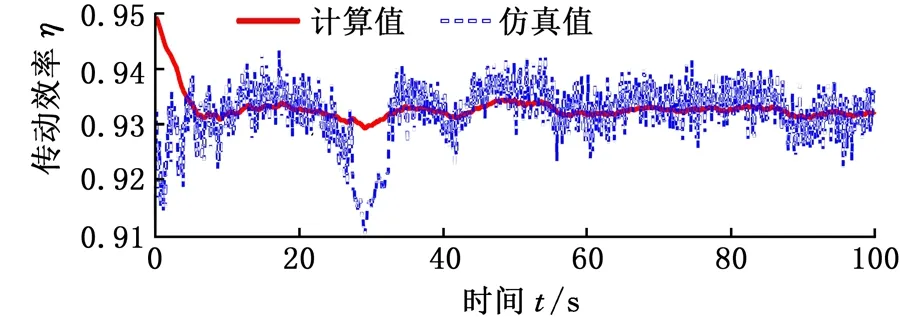
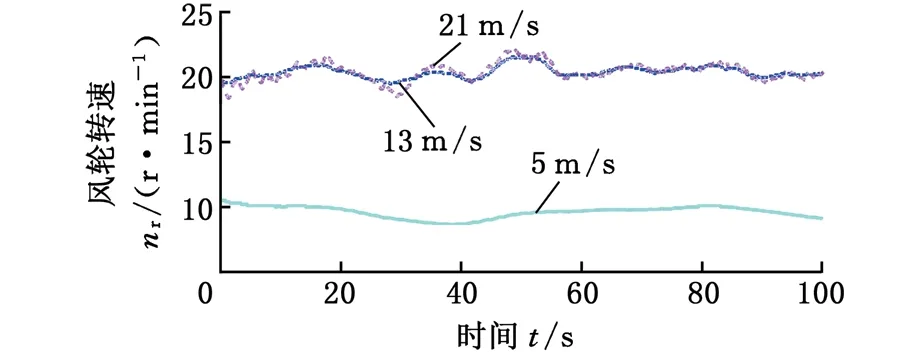
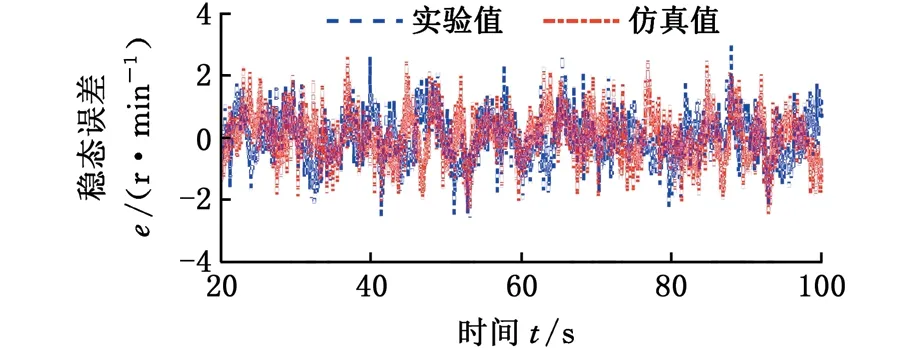
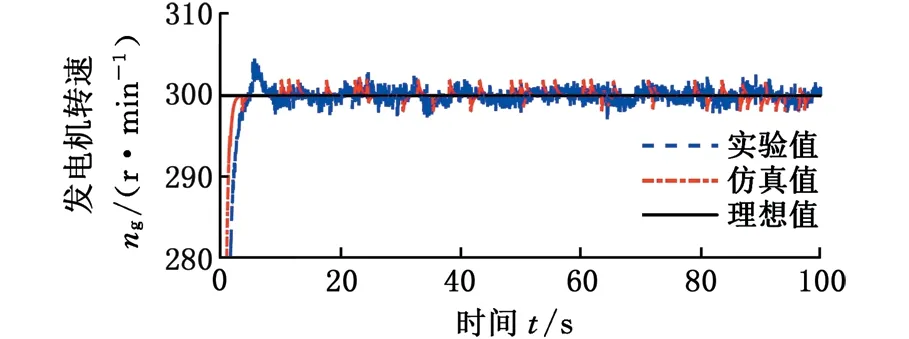
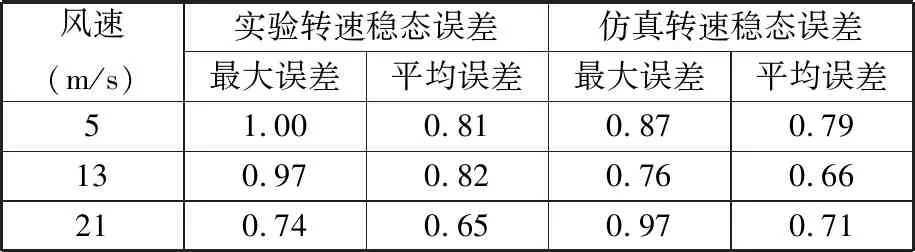
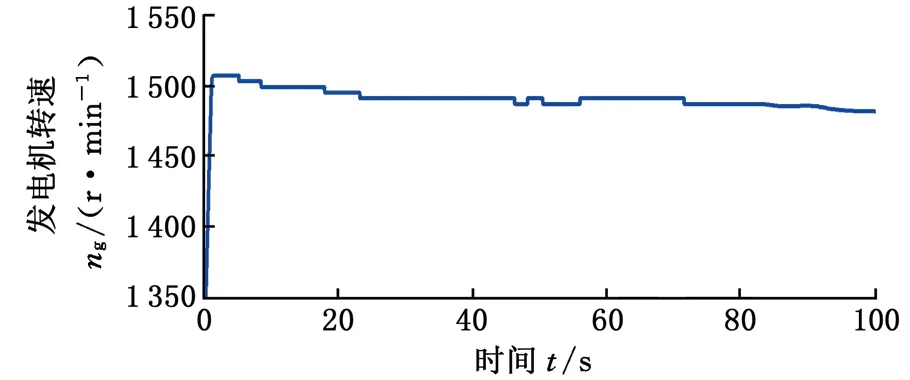
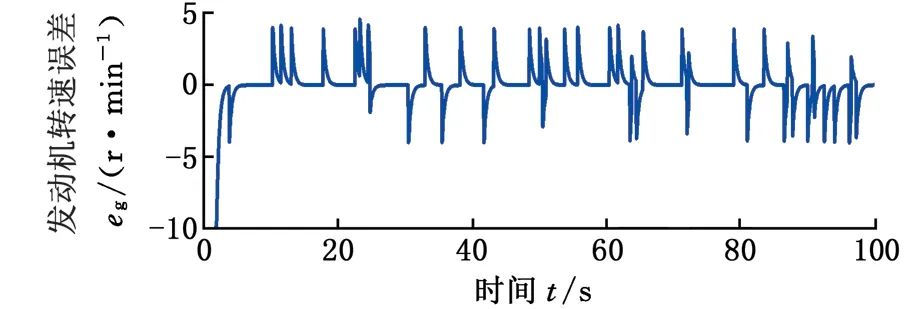
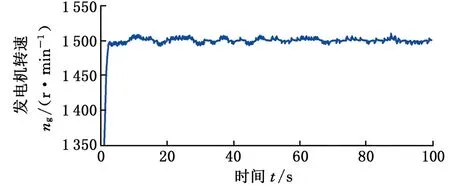
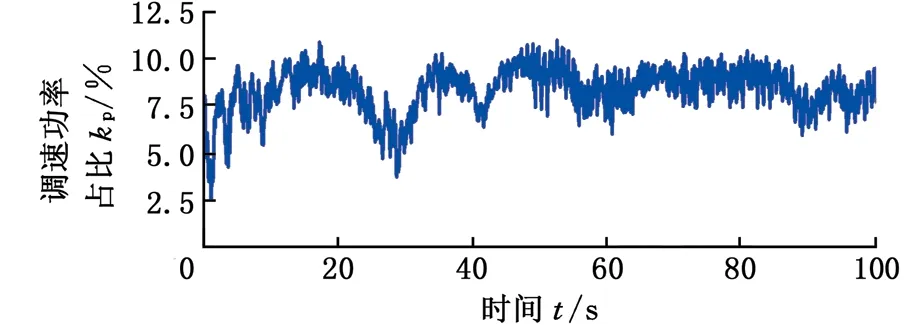
設定差動輪系主輸入構件(行星架)傳遞的轉速和功率均為正,由表1可知,總體功率流向與IRS和k的值直接相關。若IRS> 0,齒圈從風輪吸收功率,調速電機處于發電狀態,且總體功率流經行星架;若-1/k (a) IRS > 0 (b) -1/k 基于以上總體功率流向的分析,可以對所設計的差動調速風電機組傳動系統效率進行分析,從而驗證該風電機組的傳動性能滿足要求。 圖3a中,IRS> 0,總體功率流經行星架(由行星架分別流向太陽輪和齒圈)。此時,差動輪系的功率平衡方程如下: TSnS+TRnR+TCnC(ηC)τ=0τ=±1 (7) 其中,ηC為該情況下差動輪系的傳動效率。根據傳動方案,行星架連接風輪,一直處于主動狀態,因此τ= 1。依據式(1)、式(5)和式(7),ηC可通過下式計算: (8) 同理,若系統功率流向如圖3b所示,總體功率流經太陽輪,則此時的差動輪系傳動效率ηS可由下式計算: ηS= (9) 由圖1可知,差動輪系中的太陽輪與同步發電機直接連接,則發電機吸收功率為 Pg=Tgng=TSng (10) 設風輪與行星架之間的傳動效率為ηCr,則依據式(1)和式(5)可得 (11) 式中,Tr為風輪轉矩。 將式(11)代入式(10),可以得到發電機功率 (12) 同理,可得調速電機吸收或發出的功率 (13) 式中,Pr、Pm分別為風輪和調速電機傳遞的功率;ηRm為齒圈和調速電機之間的傳動效率。。 同樣分兩種情況,當總體功率流經行星架時,IRS>0且ν= 1。此時整體的傳動系統效率ηTC表示為 ηTC=|(Pg+Pm)/Pr| (14) 當總體功率流經太陽輪時,ν=-1,此時整體的傳動系統效率ηTS表示為 ηTS=|Pg/(Pr+Pm)| (15) 將式(12)、式(13)代入式(14)和式(15),可以計算得到相應條件下整體的傳動系統效率。 分析圖1可知,差動調速風電機組仿真模型主要由風輪、傳動系統、調速電機、同步發電機、電網及控制單元等模塊組成,本文只介紹差動調速風電機組傳動系統的仿真建模方法。筆者將傳動鏈簡化為包含行星架輸入軸、太陽輪輸出軸及齒圈調速軸的三軸結構(即傳動系統三軸動力學模型),如圖4所示。 圖4 傳動系統三軸動力學模型Fig.4 Three-axis modelof transmission system 由圖4可得系統三軸動力學方程(行星架輸入軸、太陽輪輸出軸和齒圈調速軸)的表達式分別如下: (16) (17) (18) 式中,Jr、Jg和Jm分別為風輪、發電機和調速電機的等效轉動慣量;Tg、Tm為發電機和調速電機轉矩;θC、θS和θR為行星架、太陽輪和齒圈的轉動角位移;θr、θg和θm為風輪、發電機轉子和調速電機轉子的角位移;BC、BS和BR分別為行星架軸、太陽輪軸和齒圈軸的阻尼;KC、KS和KR分別為行星架軸、太陽輪軸和齒圈軸的扭轉剛度。 結合上述三軸動力學方程,筆者建立了差動調速風電機組仿真模型。模型中調速電機與同步發電機均采用Simulink自帶模塊。由于簡化的三軸動力學模型可能造成的建模誤差,筆者利用圖5所示的試驗臺對仿真模型進行驗證實驗。 圖5 試驗臺原型和設備Fig.5 The prototype and equipment of the test bench 試驗臺硬件主要包括:上位機、模擬風輪的伺服電動機、差動輪系、同步發電機、伺服調速電機、伺服驅動器、傳感器及試驗臺控制系統。軟件則由DAQNavi驅動和LabVIEW開發環境組成。在仿真模型驗證實驗中,依據試驗臺實際數據建立仿真模型。利用FAST軟件,當湍流強度為20%時,得到平均風速為5 m/s、13 m/s、21 m/s時的正常湍流風速模型,及對應的風輪轉速見圖6。 (a)FAST仿真風速 (b)不同風速下風輪轉速圖6 FAST風輪仿真結果Fig.6 Simulation results of wind rotor via FAST 將此風輪轉速作為仿真模型和試驗臺的輸入,設定發電機理想轉速為300 r/min,時間為100 s,并對仿真模型進行驗證。通過仿真和實驗分別得到3種風速條件下(v=5 m/s、13 m/s和21 m/s)發電機轉速與理想值的對比,見圖7~圖9。其中,穩態誤差是指風電機組進入穩態運行后的轉速誤差。 (a)發電機轉速 (b)輸出轉速穩態誤差圖7 5 m/s風速時同步發電機轉速實驗和仿真對比結果Fig.7 Comparative results of synchronous generator speed via experiment and simulation under 5 m/s wind speed (a)發電機轉速 (b)輸出轉速穩態誤差圖8 13 m/s風速時同步發電機轉速實驗和仿真對比結果Fig.8 Comparative results of synchronous generator speed via experiment and simulation under 13 m/s wind speed (a)發電機轉速 (b)輸出轉速穩態誤差圖9 21 m/s風速時同步發電機轉速實驗和仿真對比結果Fig.9 Comparative results of synchronous generator speed via experiment and simulation under 21 m/s wind speed 為了更好地分析結果,在不同風速條件下,仿真和實驗得到的輸出轉速偏離理想值的誤差見表2。由表2可知,在不同風速條件下,與理想值相比,通過實驗和仿真得到的輸出轉速穩態最大誤差均小于1%,穩態平均誤差小于0.82%,從而驗證了仿真模型的準確性。 表2 輸出轉速穩態誤差數據分析 基于以上分析,建立1.5 MW差動調速風電機組仿真模型。其中,發電機額定轉速為1 500 r/min,轉矩為9 550 N·m,功率為1 500 kW;結構參數k=2;調速電機額定功率為300 kW;風輪半徑為30 m,慣量為55 600 kg·m2;軸剛度為5.6×106N·m/rad,阻尼為0.5 N·m·s/rad。同樣將圖6所示的風輪仿真數據作為輸入,最終分別得到3種風速條件下(v=5 m/s、13 m/s和21 m/s)的功率仿真結果,見圖10~圖12。 (a)發電機轉速 (b)發電機轉速誤差 (c)各單元傳遞功率 (d)調速電機所需功率占比圖10 5 m/s風速時仿真結果Fig.10 Simulation results under 5 m/s wind speed (a)發電機轉速 (b)發電機轉速誤差 (c)各單元傳遞功率 (d)調速電機所需功率占比圖11 13 m/s風速時仿真結果Fig.11 Simulation results under 13 m/s wind speed 由圖10a、圖11a和圖12a可知,在不同風速條件下,同步發電機轉速可以被差動調速系統實時調節,穩定在1 500 r/min。由圖10b、圖11b和圖12b可知,在5 m/s、13 m/s、21 m/s風速條件下,通過計算可得到輸出轉速穩態最大誤差依次為1.23%、0.31%和0.68%,穩態平均誤差依次為1.08%、0.25%和0.48%。由圖10c、圖11c和圖12c可知,在不同風速條件下,調速電機所需的最大功率較小。由圖10d、圖11d、圖12d可知,在5 m/s、13 m/s、21 m/s風速條件下,調速功率分別占發電機功率的15.47%、7.71%和10.97%,實現了風電機組在無需大功率變頻設備下的變速恒頻。 同時根據仿真結果,得到3種不同風速條件下的機組傳動效率,與式(14)、式(15)的效率計算值進行比較,其中ηH、ηCr、ηRm分別取0.97、0.95和0.98,得到對比結果見圖13。 由圖13可知,差動調速風電機組的傳動系統效率較高,在5 m/s風速條件下,傳動系統效率達到0.951。同時,傳動系統效率的計算值和仿真值具有相同的變化規律,且基本吻合;計算值和仿真值在5 m/s、13 m/s和21 m/s風速條件下最大偏差依次為0.16%、1.06%和2.15%,驗證了效率分析的正確性。 (a)發電機轉速 (b)發電機轉速誤差 (c)各單元傳遞功率 (d)調速電機所需功率占比圖12 21 m/s風速時仿真結果Fig.12 Simulation results under 21 m/s wind speed (1)傳動系統總體功率流向與轉速比IRS直接相關。當IRS=nC/nS=1/(1+k) 時,調速系統處于臨界狀態,調速電機不提供也不吸收功率,且機組整體的傳動系統效率較高,最高可達到0.951。 (2)在不同風速輸入條件下,差動調速系統可實現發電機輸出轉速穩態誤差小于1.23%,且調速端所需功率占發電機功率的比值小于15.47%。相比于現有機組變頻設備,有效減少了能量損耗,驗證了差動調速風電機組的可行性和優越性。 本研究為后期差動調速風電機組設計與優化提供了一定的參考。但在今后的研究與實際工程應用中,相關結構形式以及臨界狀態分析還可進一步完善。 (a)輸入風速5 m/s (b)輸入風速13 m/s (c)輸入風速21 m/s圖13 不同風速條件下傳動效率仿真與計算值對比結果Fig.13 Comparative results of efficiency valves of the simulation and calculation under different wind speed conditions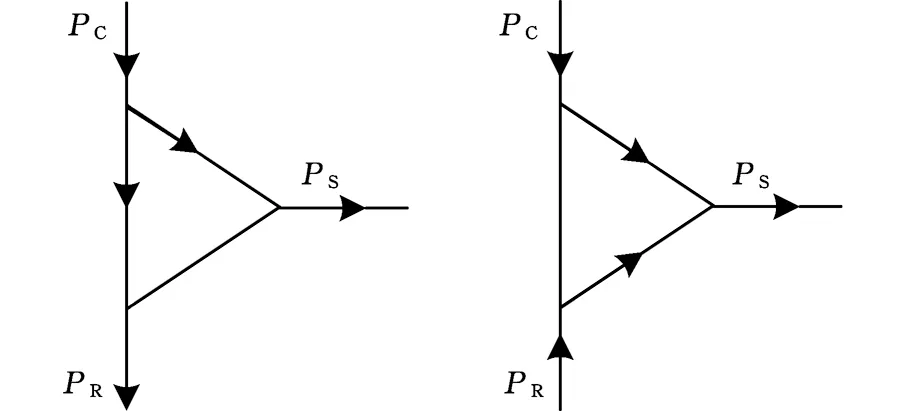
2.2 傳動效率分析
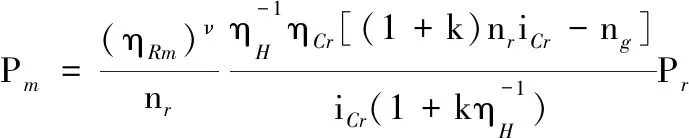
3 數值仿真與實驗驗證
3.1 仿真模型的實驗驗證







3.2 1.5 MW差動調速風電機組仿真分析








4 結論