基于狀態空間模型的數控機床熱誤差建模

苗恩銘 呂玄玄 魏新園 宋先進 董云飛

1.重慶理工大學機械工程學院，重慶,4000542.合肥工業大學儀器科學與光電工程學院，合肥,230009

0 引言

對于數控機床熱誤差補償，其補償模型精度是影響最終補償效果的主要因素[1-4]。許多研究發現，補償模型的熱誤差擬合精度高，但并不代表模型能夠長期準確地預測機床熱誤差[5-8]。

人們對數控機床熱誤差補償控制技術的研究多集中在建模理論與應用方面。LO等[9]采用相關性分組、典型變量搜索和分組搜索等方法，優化了溫度測點選擇，保證了機床熱誤差多元線性回歸模型的預測精度。ABDULSHAHED等[10]通過灰色模型和模糊C-均值聚類的溫度測點優化選擇方法，減少了溫度測點數量，降低了溫度傳感器的不確定性及建模自變量之間的相關性，并應用自適應神經模糊推理系統建立了機床熱誤差模型。苗恩銘等[11-12]提出模糊聚類結合灰色關聯度的溫度測點選擇方法，減少了溫度測點數量，降低了建模自變量之間的相關性和多重共線性，建立了機床熱誤差支持向量機和多元線性回歸模型，該模型具有良好的預測精度和穩健性；并進一步提出了機床熱誤差補償建模最佳轉速狀態的選擇方法[13]，比對分析了機床在主軸空轉和實切狀態下的熱特性差異，且基于田口實驗方法實現了實切狀態下熱誤差補償實驗方案的優化設計[14]。張偉等[15]采用灰色關聯分析和模糊聚類分析結合的方法對機床溫度測點進行優化選擇，保證了機床熱誤差模型的預測精度。李艷等[16]采用互信息和改進模糊聚類相結合的方法對機床溫度測點進行優化選擇，顯著提高了機床熱誤差模型預測精度。上述研究通過對建模溫度測點的優化選擇，有效提升了模型準確反映機床熱誤差與溫度之間變化規律的能力，從而保證了熱誤差模型的預測精度。通常，選出的建模溫度測點稱為溫度敏感點。目前，模糊聚類結合灰色關聯度算法是應用較為廣泛的溫度敏感點選擇方法[5,11-12,15-16]。

我們通過大量實驗研究發現，當機床運行參數發生變化時，熱誤差與溫度之間的變化規律也會隨之改變。當進行熱誤差預測時，機床很可能會在不同的參數設置條件下運行，熱誤差規律的差異性也會導致模型預測精度降低。為此，本文在目前傳統熱誤差建模算法研究的基礎上，提出了基于狀態空間模型的數控機床熱誤差建模方法。該方法綜合考慮了溫度敏感點溫升、主軸轉速對機床熱誤差的影響，使模型可根據機床運行參數的變化而自動調整，且模型對機床運行參數變化具有良好的自適應性，從而為提升機床熱誤差模型的預測精度提供了有利條件。

1 機床運行參數變化對熱誤差模型預測精度的影響

為驗證機床熱誤差狀態空間模型的預測精度，本文以一臺Leaderway V-450型數控機床為實驗對象，在不同主軸轉速條件下進行實驗。實驗結果表明：當采用傳統算法(本文以多元線性回歸算法為例)在一定轉速下建立熱誤差模型,對不同轉速下的實驗數據進行預測時，相比于對相同轉速下的實驗數據進行預測，其模型預測精度降低，表明機床運行參數的變化確實會導致熱誤差規律發生變化。對機床熱誤差多元線性回歸模型和狀態空間模型的預測精度進行比對分析，實驗結果表明：狀態空間模型具有更高的預測精度和穩健性，從而驗證了機床熱誤差狀態空間模型的優越性。

1.1 模糊聚類結合灰色關聯度算法

為降低各溫度變量之間的相關性和多重共線性對模型預測精度的影響，在進行機床熱誤差建模時，首先應進行建模溫度測點的優化選擇(即溫度敏感點選擇)。本文采用模糊聚類結合灰色關聯度的溫度敏感點選擇方法，有效降低了各溫度變量之間的相關性和多重共線性，為機床熱誤差模型預測精度的提高提供了保障，具體如下。

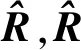
(1)

式中，t為不同時刻，是離散的測量時間點；L為實驗數據長度。

(2)灰色關聯度。采用鄧氏關聯度計算表達式獲得機床熱誤差y與各溫度變量xi(i=1,2,…,n)之間的灰色關聯度γ(y,xi)，灰色關聯度越大，溫度測點對機床熱誤差的影響權重越大。選擇出每類中與熱誤差關聯度最大的溫度測點作為溫度敏感點，并參與建模，從而避免同類中溫度變量間的強關聯度對熱誤差模型預測精度的影響，同時，減少了使用的溫度傳感器數量。灰色關聯度γ(y,xi)按下式計算：

(2)

r(y(t),xi(t))=

(3)

式中，ρ為分辨系數，ρ∈[0,1]，一般取ρ=0.5。

對溫度敏感點進行選擇后，將其作為自變量，通過多元線性回歸算法即可建立機床熱誤差模型：

y=β0+β1x1+…+βmxm

(4)

式中，x1、x2、…、xm分別為不同的溫度敏感點溫升；β0、β1、…、βm為模型參數。

1.2 機床熱誤差實驗

轉速是機床主要的運行參數之一，為減少外界環境對實驗結果的影響，在同一季度內，本文通過改變主軸轉速來使機床處于不同的運行參數條件下。以Z向熱誤差為例，實驗選擇溫度傳感器DS18B20(測量精度為±0.5 ℃，最大分辨能力為0.062 5 ℃)采集溫度數據，參考國際標準ISO 230-3:2007[17]給出的熱誤差測量方法，選擇電渦流傳感器(測量精度為±1 μm)采集機床主軸Z向熱誤差。溫度傳感器的貼放位置以影響機床主軸Z向熱誤差的主要熱源附近為主，溫度傳感器T1～T9(對應的溫度敏感點分別為T1～T9)和電渦流傳感器S的安放位置見圖1。溫度傳感器T10安放在機床外殼上以測量環境溫度，未出現在圖1中。各傳感器的安放位置及作用見表1。實驗裝置如圖2所示。

圖1 傳感器安放位置示意圖Fig.1 Sketch map of sensor placement

傳感器安放位置作用T1～T5主軸前端測量主軸發熱T6,T9主軸套測量主軸發熱T7打刀缸底座測量主軸發熱T8主軸電機測量電機發熱T10機床外殼測量環境溫度SZ向正下端測量主軸熱誤差

圖2 實驗裝置實物圖Fig.2 Physical map of experimental device

測量時，主軸以恒定轉速(2 000 r/min、4 000 r/min、6 000 r/min)轉動，每隔3 min主軸停轉一次，以測量主軸Z向熱誤差，并通過溫度測量系統采集該時刻的溫度數據。測量實驗持續時間均達4 h以上。

本研究共進行了6批次實驗，分別記為K1～K6，各批次實驗主軸轉速的設置見表2，測得6批次實驗數據的熱誤差曲線見圖3。以K1批次實驗數據為例，圖4給出了各溫度曲線。

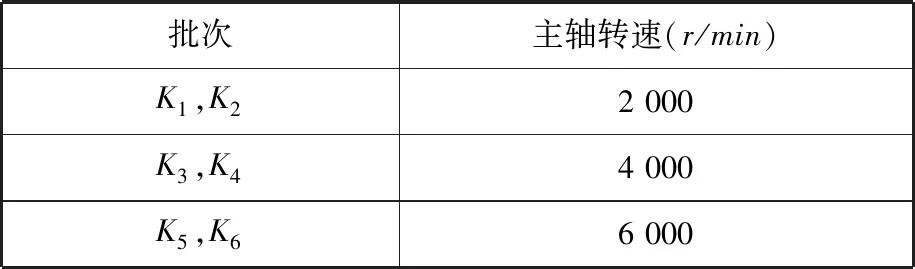
表2 各批次實驗主軸轉速設置

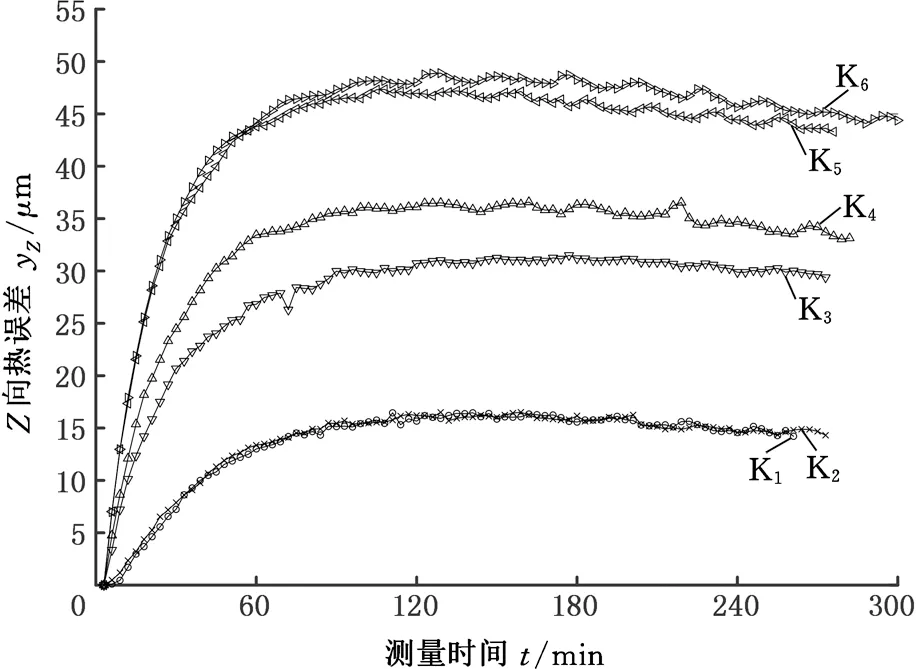
圖3 K1～K6批次實驗數據的熱誤差曲線Fig.3 Thermal error curves of K1～K6 batch experimental data

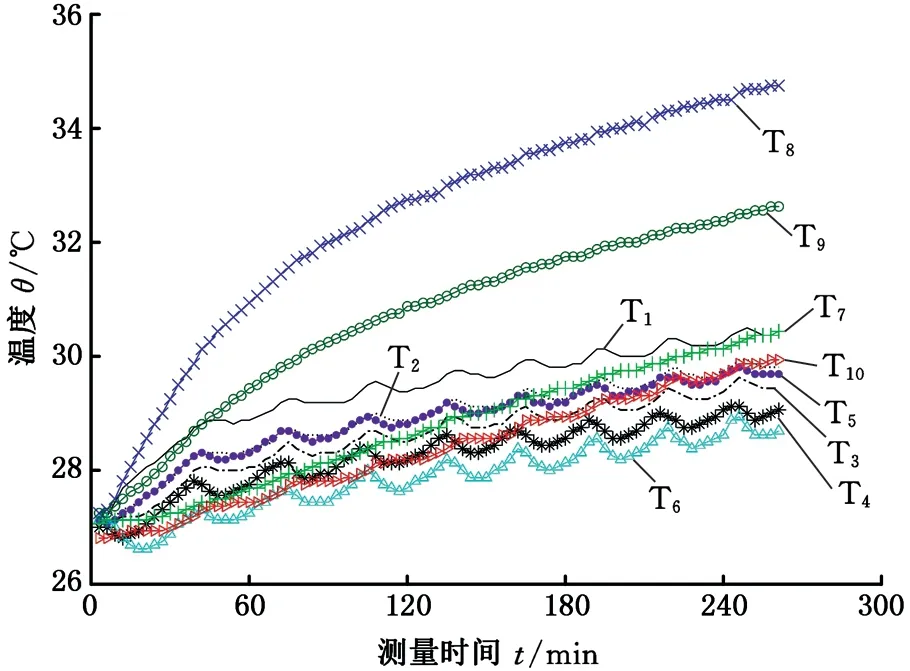
圖4 K1批次實驗數據的溫度曲線Fig.4 Temperature curves of K1batch experimental data

1.3 機床運行參數變化條件下熱誤差模型預測精度分析

采用模糊聚類結合灰色關聯度算法對K1～K6批次實驗數據的溫度敏感點進行選擇，溫度敏感點的選擇結果均為T1、T7。采用多元線性回歸算法，分別獲得K1～K6批次實驗數據的機床Z向熱誤差多元線性回歸模型，分別記為模型M1～M6。

M1：yZ=-1.67+9.82ΔT1-4.09ΔT7
M2：yZ=-3.03+8.65ΔT1-2.57ΔT7
?
M6：yZ=-4.01+7.15ΔT1-3.81ΔT7

式中，yZ為機床Z向熱誤差測量值；ΔT1、ΔT7分別為溫度敏感點T1和T7的溫升。

進而分別利用模型M1～M6對K1～K6批次實驗數據進行擬合或預測，并計算出各模型對每批次實驗數據的擬合或預測殘余標準差S[18]。殘余標準差S越小，表明擬合或預測誤差越小，精度越高。殘余標準差S的計算公式為

(5)

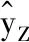
同一轉速下的兩個模型對同一轉速下兩批次數據的預測殘余標準差S的平均值記為SCM，即

(6)

式中，I、J分別為轉速相同的模型編號和實驗批次。

SCM的計算結果見表3，并將表3中的計算結果繪制成條形圖，如圖5所示。

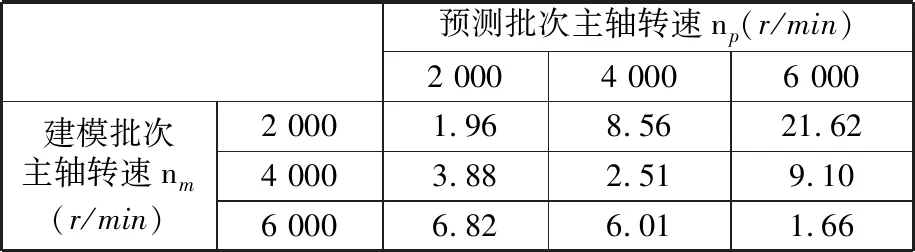
表3 不同轉速下模型對各轉速熱誤差預測殘余標準差平均值

圖5 不同轉速下模型對各轉速熱誤差預測殘余標準差平均值Fig.5 Average of predicted residual standard deviation of thermal error for each rotational speed by different speed models

從圖5中可以看出，機床熱誤差多元線性回歸模型對相同轉速(nm=np)下得到的熱誤差數據的預測殘余標準差平均值，明顯小于對不同轉速(nm≠np)下得到的熱誤差數據的預測殘余標準差平均值，這表明當數控機床轉速發生變化時，會導致機床熱誤差規律發生改變，從而引起熱誤差模型預測精度降低。

2 機床熱誤差狀態空間模型

狀態空間模型的系統輸出包含系統輸入、系統自身特性、系統同外界相互聯系三者信息，因此狀態空間模型不僅可以描述系統輸入與輸出之間的關系，還能更好地揭示系統的內部結構和特性，對系統運行參數變化具有良好的適應能力[19]。為提升機床熱誤差模型在機床不同運行參數條件下的模型預測精度，本文建立以溫度敏感點溫升與主軸轉速為輸入的機床熱誤差狀態空間模型，用于數控機床熱誤差預測。

2.1 機床熱誤差狀態空間模型建立

將溫度敏感點的溫升ΔT1、ΔT7和該批次實驗數據主軸轉速nm作為輸入，機床Z向熱誤差yZ(t)作為輸出，建立機床熱誤差狀態空間模型如下：

x(t+1)=Ax(t)+Bu(t)

(7)

yZ(t)=Cx(t)+Du(t)

(8)

u(t)=(ΔT1(t),ΔT7(t),nm(t))T

x(t)=(x1(t),x2(t),x3(t))T

C=(1,0,0)D=(d1,d2,d3)

式中，u(t)為系統的輸入向量；x(t)為系統自身的狀態向量;A為系統自身的結構矩陣；B為系統的參數矩陣；C、D均為系統的參數向量;a1、a2、a3為矩陣A中的元素數值；b11、b12、…、b33為矩陣B內的元素數值；d1、d2、d3為向量D中的元素數值。

2.2 機床熱誤差狀態空間模型參數辨識

本文用最小二乘算法估計模型的參數，用狀態觀測器估計系統的狀態[20]，基本過程如下。

(1)聯合式(7)和式(8)可得到機床Z向熱誤差狀態空間模型的參數辨識模型：

yZ(t)=x1(t)+Du(t)=HT(t)a+TT(t)b

(9)

a=(a1,a2,a3)T

b=(d1,d2,d3,b11,b21,b31,b12,b22,b32,b13,b23,b33)T

H(t)=[-x3(t-3) -x2(t-3) -x1(t-3)]T

T(t)=[ΔT1(t) ΔT7(t)nm(t) ΔT1(t-1)

ΔT1(t-2) ΔT1(t-3) ΔT7(t-1) ΔT7(t-2)

ΔT7(t-3)nm(t-1)nm(t-2)nm(t-3)]T

定義相關堆積矩陣Y=[yZ(1)yZ(2) …

yZ(L)]T，H=[H(1)H(2) …H(L)]T，T=[T(1)T(2) …T(L)]T，則式(9)可等價為

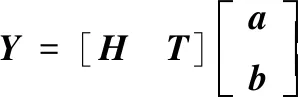
(10)

因此，可獲得基于最小二乘算法的機床Z向熱誤差狀態空間模型參數估計，即

(11)

由于式(11)對應的求逆矩陣在每次計算過程中均含不變的子矩陣和變化的子矩陣，為減少計算量，本文利用分塊矩陣求逆引理，得到機床Z向熱誤差狀態空間模型基于最小二乘算法的參數估計等價表達式，即

(12)

α=βTTYβ=inv(TTT)

Q=HTMHM=I-TβTT

式中，I為L行L列的單位矩陣。

(2)本文通過設置初始狀態向量x(1)=(1,1,1)T/p0(此處參數p0取106)，并利用上述熱誤差狀態空間模型參數估計結果，依據式(7)(即狀態觀測器)獲得熱誤差狀態空間模型中未知的狀態向量x(t)=(x1(t),x2(t),x3(t))T。

(3)在給定辨識精度q0條件下，利用迭代方案獲得模型參數向量CO=(a,b)T，并建立機床Z向熱誤差狀態空間模型。機床Z向熱誤差狀態空間模型參數辨識流程見圖6，其中q=‖CO,k-CO,k-1‖，CO,k-1、CO,k分別為第k-1次和第k次迭代熱誤差狀態空間模型參數向量CO的估計結果。

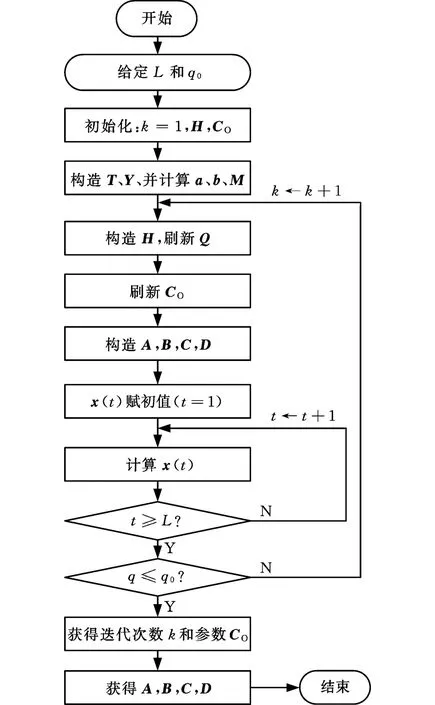
圖6 機床熱誤差狀態空間模型參數辨識流程圖Fig.6 Machine thermal error state space model parameter identification flow chart

根據上述步驟，建立K1～K6批次實驗數據的機床Z向熱誤差狀態空間模型N1～N6，結果如下。

Ni：x(t+1)=Aix(t)+Biu(t)

yZ(t)=Cix(t)+Diu(t)i=1，2，…，6

?

?

C1=C2=…=C6=(1,0,0)

D1=(0.37，0.19，4.60×10-5)

D2=(0.38，0.26，2.26×10-4)

?

D6=(0.55，-0.21，1.07×10-3)

3 預測精度比對

為了對機床熱誤差多元線性回歸模型、狀態空間模型進行比對分析，分別利用多元線性回歸模型M1～M6及狀態空間模型N1～N6對K1～K6批次熱誤差數據進行擬合或預測。根據式(5)計算得到各模型對每批次實驗數據的預測殘余標準差S，并計算各模型對應所有預測殘余標準差(可反映模型預測精度)S的均值參數SM和離散標準差參數SS，計算結果分別見圖7和圖8。SM、SS計算公式分別為

(13)

(14)

其中，對于M1～M6、N1～N6中的每個模型，Si為該模型對Ki(i=1,2,…,6)批次實驗數據的預測殘余標準差。模型預測精度均值參數SM小，表明模型的平均預測精度高；模型預測精度離散標準差參數SS小，表明模型對各批次熱誤差數據預測精度的分散程度小，各批次實驗轉速變化對預測精度的影響較小。

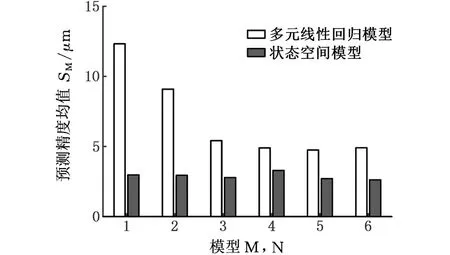
圖7 機床熱誤差模型預測精度均值Fig.7 Average of prediction accuracy of machine tool thermal error model

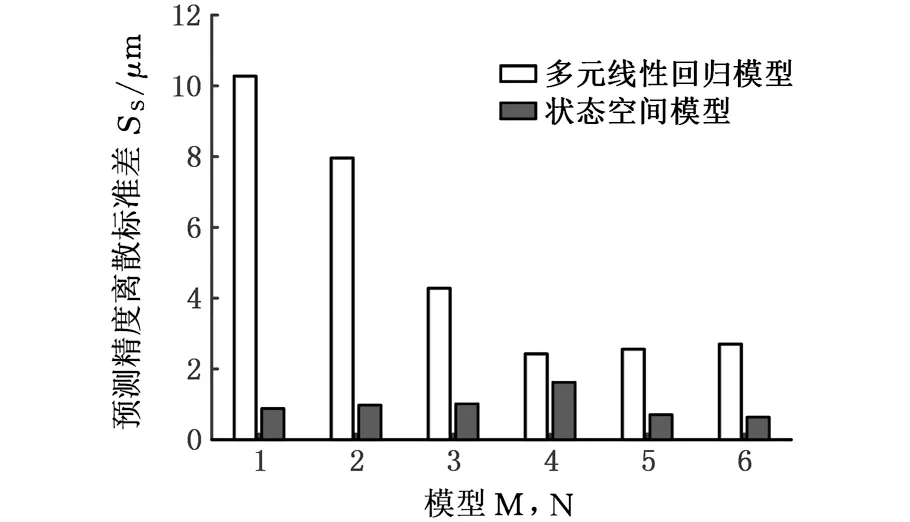
圖8 機床熱誤差模型預測精度離散標準差Fig.8 Discrete standard deviation of prediction accuracy of machine tool thermal error model

由圖7可以看出，多元線性回歸模型預測精度均值參數SM分布在4.75～12.33 μm，狀態空間模型預測精度均值參數SM分布在2.63～3.30 μm。由圖8可以看出，多元線性回歸模型預測精度離散標準差參數SS分布在2.43～10.28 μm，狀態空間模型預測精度離散標準差參數SS分布在0.64～1.62 μm。相對于多元線性回歸模型，狀態空間模型的預測精度均值和預測精度離散標準差均有所降低。

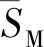
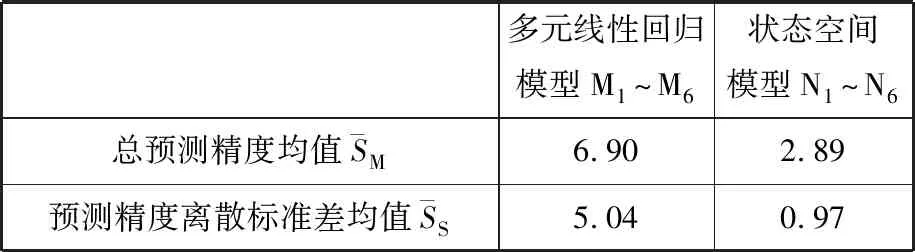
表4 兩種模型的平均預測效果

由表4可知，在不同主軸轉速下，相對于機床熱誤差多元線性回歸模型，機床熱誤差狀態空間模型的預測精度及穩健性得到了較好的提升。經計算，機床熱誤差狀態空間模型的模型預測精度總體提升58.12%。由上述分析可知，相對于機床熱誤差多元線性回歸模型，機床熱誤差狀態空間模型實現了機床熱誤差、溫度敏感點溫升及主軸轉速之間作用關系的綜合描述，使模型可根據機床運行參數變化而自動調整，模型對機床運行參數變化具有良好的自適應性，較好地提升了模型的預測精度和穩健性。

4 實驗驗證

為驗證數控機床熱誤差狀態空間模型補償效果，將模型N1存儲到機床補償卡系統中，分別在熱誤差補償控制系統關閉、開啟狀態下，在Leaderway V-450型數控機床上，采用可轉位面銑刀對鑄鐵進行平面切削加工實驗。加工實驗開始前，主軸以轉速為6 000 r/min空轉3 h；加工過程中，主軸轉速1 000 r/min、進給速度300 mm/min、切削深度300 μm，切削過程持續15 min。加工試件見圖9，其中，①為參考平面，②為未補償加工平面，③為補償加工平面。采用德國蔡司MC850三坐標測量機(測量范圍為850 mm×700 mm×600 mm，分辨能力為0.1 μm)對切削加工試件進行均布9點檢測，測試結果見表5。

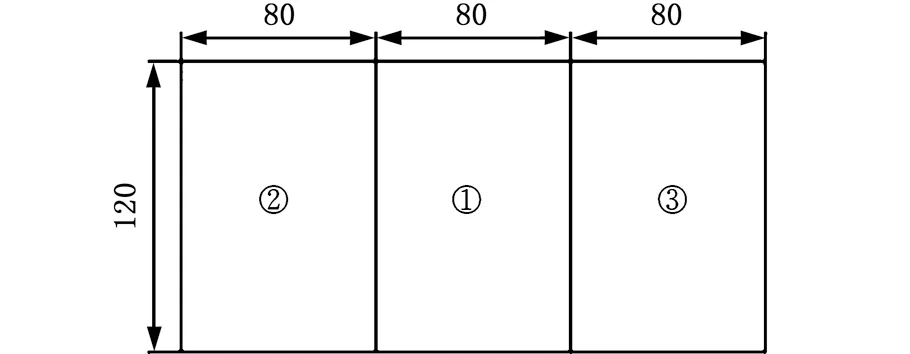
圖9 加工試件示意圖Fig.9 Processing specimen schematic

μm

由表5可知，相對于未補償時的平均誤差量，補償時的平均誤差量減少了85.5%。結果表明：基于狀態空間模型的機床熱誤差補償技術的實施，可獲得很好的加工補償效果，有效地提高了數控機床加工精度。

5 結論

(1)針對目前關于熱誤差建模的研究中忽略了機床運行參數變化對模型精度影響的問題，本文提出了基于狀態空間模型的數控機床熱誤差建模方法。

(2)以不同主軸轉速條件下的Leaderway V-450型數控加工中心為研究對象，分別建立機床熱誤差多元線性回歸模型和狀態空間模型，結果表明：與多元線性回歸模型相比較，狀態空間模型的預測精度及穩健性得到了有效提升。

(3)采用Leaderway V-450型數控加工中心進行了實際切削加工條件下的熱誤差補償實驗，結果表明：機床熱誤差狀態空間模型的應用補償效果顯著。