糾單個有序刪除和擦除錯誤碼的構造方法*

何雅萍，賀玉成，周 林

(華僑大學廈門市移動多媒體通信重點實驗室，福建 廈門 361021)

0 引 言

在通信和存儲系統(tǒng)的傳輸過程中，由于數(shù)據(jù)同步錯誤或信道中存在噪聲、時序等干擾引發(fā)傳輸差錯，所接收到的信息可能存在元素插入、刪除、擦除和替換等錯誤[1］。為了糾正接收信息中存在的錯誤，以得到正確的傳輸信息，Varshamov和Tenengolt首先提出以他們名字命名的Varshamov-Tenengolt（VT）碼，可以糾正信道傳輸過程中發(fā)生的非對稱錯誤[2］。隨后，Levenshtein提出了一種可以糾正單個插入或者刪除錯誤的二進制碼[3］，并且在此基礎上提出了一種新的構造方法，可以糾正兩個相鄰插入或刪除錯誤[4］。多年來，學者們一直致力于構造具有更高糾錯能力的二進制碼[5-6］和非二進制碼[7-9］，并根據(jù)構造方法設計相應的簡單高效譯碼方法。

最近，Gabrys等人針對元素刪除和擦除錯誤提出了四種錯誤模型，并構造出可糾正多個刪除錯誤的方法[10］。本文研究了傳輸信息發(fā)生刪除的位置始終在擦除前的有序刪除和擦除錯誤，結合現(xiàn)有的糾錯碼構造方法，提出了一種可以糾正單個有序刪除和擦除錯誤的二進制碼的構造方法及其譯碼方法。

1 基本理論

1.1 有序刪除和擦除錯誤

對于整數(shù)n≥ 2，α=(α1,α2,…,αn)∈GF(2)n為一個碼長為n的二進制傳輸碼字，β表示接收碼字。

定義1：對于整數(shù)1≤d≤e≤n，α中第d位αd被刪除，第e+1位αe+1被擦除，且刪除位置始終在擦除位置前，稱為“單個有序刪除和擦除錯誤”，記為Fd,e(α):=β=(β1,…,βn-1)，其中

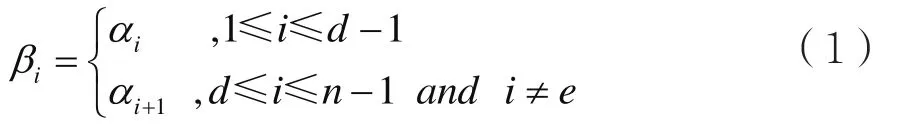
當e≤n-1時，擦除值βe=?；當e=n時，β僅發(fā)生刪除錯誤，無擦除錯誤。

例 1：設α=(0,0,1,0,1,1,0,1)，d=3，e=6，由定義1可得β=(0,0,0,1,1,?,1)。

1.2 Varshamov-Tenengolts碼

為了糾正信道傳輸過程中發(fā)生的非對稱錯誤，文獻[2］中提出了VT碼的構造方法。

定義2：對于給定正整數(shù)a∈?n，VT碼VTa(n)的定義如下：

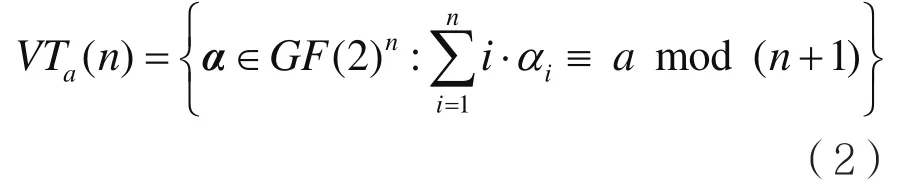
可以糾正單個刪除錯誤。

2 構造與譯碼方法

本節(jié)針對傳輸過程中發(fā)生的單個有序刪除和擦除錯誤，利用定義2的VT碼，提出一種新的構造方法，并在證明過程中給出了相應的譯碼方法。

構造：給定整數(shù)n≥2，0≤a1≤2和0≤a2≤n，二進制碼

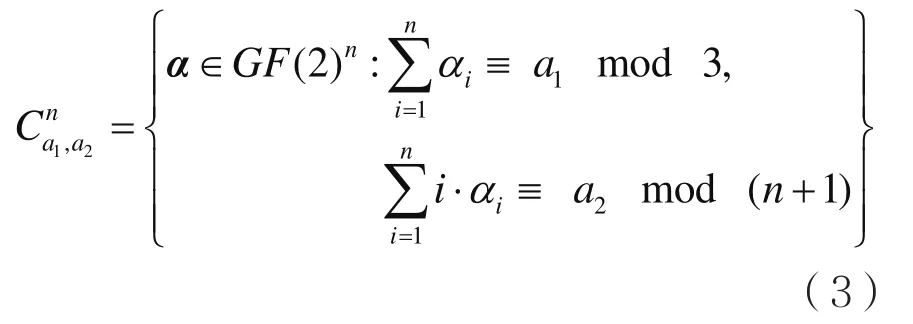
首先，分析刪除錯誤和擦除錯誤都發(fā)生的情況，隨后再分析僅發(fā)生刪除錯誤的情況。假定k∈[e］表示刪除位置d的可能值，為刪除和擦除值，其校驗和

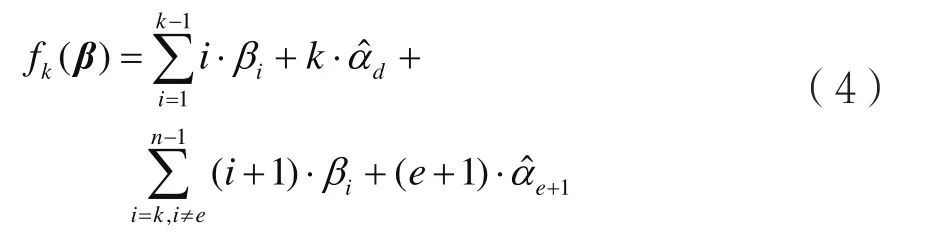
當且僅當如下兩個條件同時滿足：

（2）αk位于刪除值αd所處的游程中，即存在d1≤k，d≤d2，對任意j∈ [d1,d2］，有αk=αd=αj，αd1-1=αd2+1=1-αd1。

此時，和fk(β)之間的關系為：

fk(β)-a2≡ 0 mod (n+1)

下面，對fk(·)分情況討論。

（1）1≤k≤d

由式（1）可知，式（4）第一項求和式可表示為：

第二項求和式可表示為：

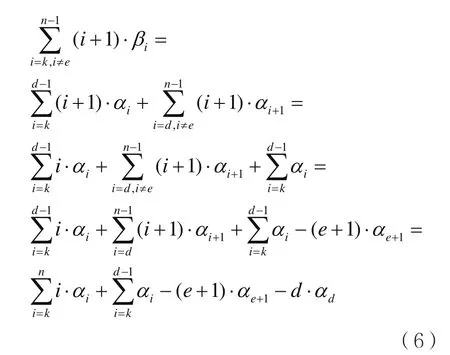
將式（5）和式（6）代入式（4）可得：

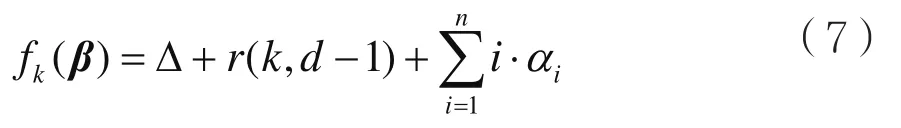
其中：

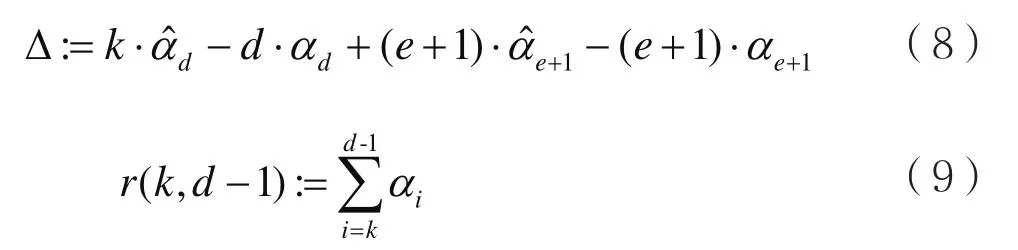
當a＜b時，

綜上，當1≤k≤d時：

（2）d+1≤k≤e

由式（1）可知，式（4）第一項求和式可表示為：

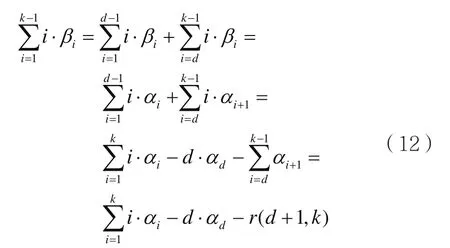
第二項求和式可表示為：

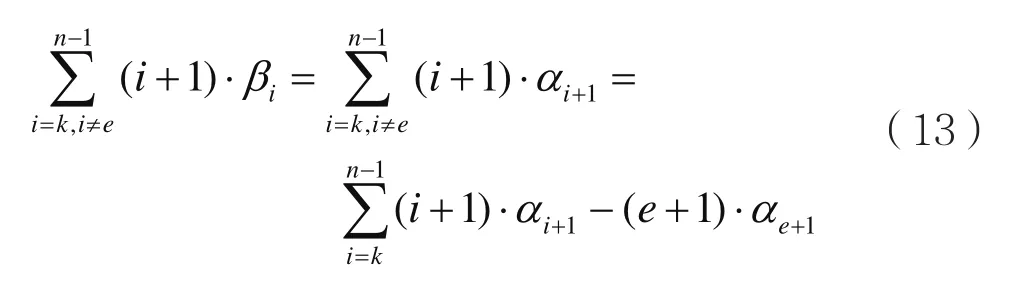
將式（12）和式（13）代入式（4）可得：

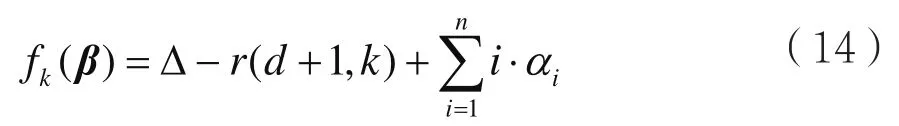
綜上，當d+1≤k≤e時，

為了恢復刪除值αd和擦除值αe+1，根據(jù)構造式（3）可得差值表達式為：

下面分別考慮D(β)存在的3種可能結果：

（1）D(β)=0

在這種情況下，刪除值αd和擦除值αe+1均為0，設定此時，式（8）中Δ=0。存在任意j(d1≤d,j≤d2)，有αj=0，αd1-1=αd2+1=1。也就是說(αd1,…,αd2)為一個0的游程，刪除位αd位于該游程中。

當1≤k≤d1-1時，在位置k和d-1之間至少存在一位值為1，使得1≤r(k,d-1)≤n，代入式（11）可得fk(β)-a20 mod (n+1)。

當d1≤k≤d時，有r(k,d-1)=0；當d+1≤k≤d2時，有r(d+1,k)=0。分別代入式（11）和式（15）均得fk(β)-a2≡ 0 mod (n+1)，其中d1≤k≤d2。

當d2+1≤k≤e時，在位置d+1和k之間至少存在一位值為1，使得-n≤-r(d+1,k)≤-1，代入式（15）可得fk(β)-a20 mod (n+1)。

（2）D(β)=2

在這種情況下，刪除值αd和擦除值αe+1均為1，設定，此時，Δ=k-d。存在任意j(d1≤d,j≤d2)，有αj=1，αd1-1=αd2+1=0。也就是說 (αd1,…,αd2)為一個1的游程，刪除位αd位于該游程中。

當1≤k≤d1-1時，在位置k和d-1之間至少存在一位值為0，使得：

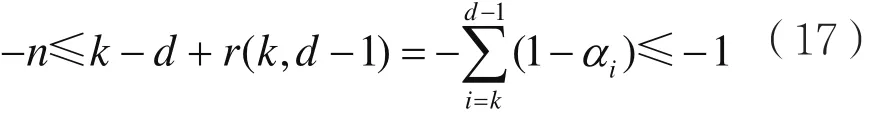
由式（11）可得fk(y)-a20 mod (n+1)。

當d1≤k≤d時， 有k-d+r(k,d-1)=0； 當d+1≤k≤d2時，分別代入式（11）和式（15）均得fk(β)-a2≡0 mod(n+1)，其中d1≤k≤d2。

當d2+1≤k≤e時，在位置d+1和k之間至少存在一位值為0，使得：

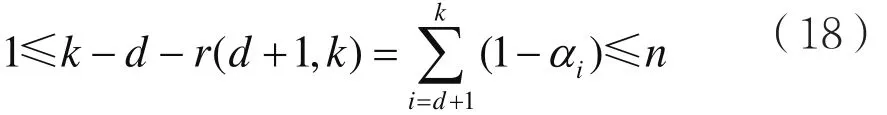
代入式（15）可得fk(β)-a20 mod (n+1)。

（3）D(β)=1

首先，假定刪除值αd=1，擦除值αe+1=0，在這種情況下：

當1≤k≤d時，由式（10）可得：

1≤-d+e+1≤-d+e+1+r(k,d-1)≤-k+e+1

代入式（11）得fk(β)-a20 mod (n+1)。

當d+1≤k≤e時，e≥-d+e+1-r(d+1,k)≥-d+e+1-(k-d)=e+1-k≥1，

代入式（15）得fk(β)-a20 mod (n+1)。

其次，假定刪除值αd=0，擦除值αe+1=1，在這種情況下：

當1≤k≤d時，-e≤k-e-1+r(k,d-1)≤k-e-1+(dk)=d-e-1≤-1，

代入式（11）得fk(β)-a20 mod (n+1)。

當d+1≤k≤e時，-1≥k-e-1-r(d+1,k)≥k-e-1-(k-d)=d-e-1≥ -e，

代入式（15）得fk(β)-a20 mod (n+1)。

最后，假定β=Fd,e(α)僅發(fā)生單個刪除錯誤，而未發(fā)生擦除錯誤。此時，設定則類 似地，當αd=0時，Δ=0，分析與情況①一致；當αd=1時，Δ=k-d，分析與情況②一致。這兩種情況都可得出，當且僅當d1≤k≤d2時，滿足fk(β)-a2≡ 0 mod (n+1)。

綜上，譯碼方法的完整步驟如算法1所示：

算法1：糾正單個有序刪除和擦除錯誤。

輸入：接收碼字β，擦除位置e（若未發(fā)生擦除錯誤，則e=n）。

輸出：恢復傳輸碼字?α。

譯碼過程：

1.初始化：k=0，F(xiàn)(0)=a2+1 mod (n+1)。

#尋找刪除位置d和擦除位置e+1

4.判斷F(k)-a20 mod (n+1)且k≤e是否成立，若成立則進入循環(huán)，重復執(zhí)行k=k+1，直到不滿足條件，跳出循環(huán)，進行下一步。

5.如果F(k)-a2≡0 mod (n+1)且k≤e，則輸出譯碼結束，不再執(zhí)行下述步驟。

6.如果fl ag=1，則輸出“譯碼錯誤”，不再執(zhí)行下述步驟。

7.如果步驟5和6均不滿足判斷條件，則重新進行初始化k=0，F(xiàn)(0)=a2+1 mod (n+1)，且設定標記fl ag=1，跳到步驟4重新開始尋找位置。

例2：令正整數(shù)n=9，d=5，e=6，假定傳輸碼字α=(0,1,1,0,0,0,1,0,1)，a1=1，a2=1，接收碼字β=(0,1,1,0,0,?,0,1)。

已知接收碼字β和擦除位置e=6，現(xiàn)根據(jù)算法1對其進行譯碼。初始化可得k=0，F(xiàn)(0)=2，由于發(fā)生擦除錯誤，且D=1，先假定標記fl ag=0。執(zhí)行步驟4，直到k=7＞6，跳出循環(huán)。由于步驟5和6均不滿足判斷條件，重新初始化k=0，F(xiàn)(0)=2，并設定標記fl ag=1，跳至步 驟 4重 新 尋 找。 當k=4＜6時，F(xiàn)(4)=21，F(xiàn)(4)-1≡0 mod 10，跳出循環(huán)。執(zhí)行步驟5，滿足判斷條件，輸出?=(0,1,1,0,0,0,1,0,1)，與原傳輸碼字α比對，譯碼正確。

3 結 語

本文結合可糾正一位刪除錯誤的VT碼，提出了一種可糾正有序刪除和擦除錯誤的二進制碼構造方法，同時給出了相應的譯碼方法。本文所提出的構造方法簡單直觀，譯碼方法具有較低的譯碼復雜度，編譯碼過程簡單，并通過實例驗證了所提出的譯碼方法的正確性。