利用遺傳BP神經網絡的調制識別新算法*

吳喜權，高 勇

（四川大學 電子信息學院，四川 成都 610065）

0 引 言

在通信技術高速發展的今天，無論是在軍事還是民用領域，通信信號的調制識別都一直是人們關注的焦點。對信號調制方式的準確識別是對信號正確解調、獲取通信信息的重要保證。因此對通信信號調制識別的研究具有十分重要的意義。

許多學者對通信信號調制方式的自動識別進行了大量的研究，其主要是基于星座圖重構[1-2］、壓縮感知理論與信號的非線性變換相結合[3-5］、相位編碼統計[6］、循環累計量[7］、二次方譜相關特征[8］、高階累積量[9］、小波變換[10］等方法提取信號特征以識別信號，對通信信號調制方式自動識別的發展做出了重要貢獻。但是這些方法也有進一步改進之處。比如，重構星座圖的減法聚類算法對不同調制階數信號要求的聚類半徑不同且難以預先確定。聚類半徑較大對高階調制信號的星座圖重構效果較差，較小則對低階調制信號星座圖重構效果較差；基于信號N次方非線性變換以及壓縮感知理論提取特征對信號進行識別，運算復雜度較高；采用相位編碼統計方法識別信號，雖然算法具有良好的抗頻偏性能，但是在實際應用中該算法相位差分的階數依賴于待識別信號的信噪比且階數越大運算量和工程實現的復雜度就會越大；利用信號循環累積量的特征對信號進行識別，需要信號載頻這一先驗信息且循環累積量運算量也較大；而基于信號的二次方譜相關特征識別信號，雖然不受信號幅度變化的影響且運算復雜度相對信號循環累積量的運算復雜度較低，但該算法也依賴于信號載頻這一先驗信息；此外只依賴于信號高階累計量的方法，在相同信號類型間識別時也不能有效區分信號。傳統的通信信號調制方式自動識別方法大多都采用二叉樹分類器結合信號特征區分信號，一般都會設定一個固定門限值。但是在低信噪比下采用傳統二叉樹分類器單靠設置固定門限去區分信號其效果不理想，且在低信噪比下判決門限也不易選取，門限設定恰當與否直接影響識別的性能。

為此，利用信號高階累積量、瞬時幅度譜以及信號N次方非線性變換后的特征提取新的參數并采用遺傳算法優化的BP神經網絡作為分類器識別信號。實驗結果表明在低信噪比下對2FSK、BPSK、QPSK、UQPSK、8PSK等5種通信中常用信號能有效識別。

1 特征提取

1.1 信號瞬時幅度譜

接收端含噪聲的數字調制信號經下變頻后可表示為[9］:

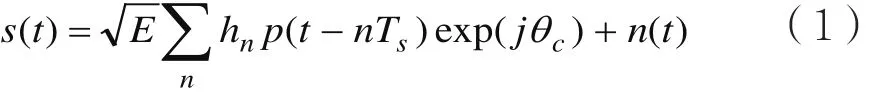
式中，p(t)是發送碼元波形，Ts為碼元寬度，θc為載波相位，hn為發送碼元序列，E為發送碼元波形的能量。n(t)為零均值的復高斯白噪聲。

定義信號的瞬時幅度譜為：

式中，I、Q為信號的同相和正交分量，FT(?)表示傅里葉變換。如圖1所示，BPSK、QPSK、UQPSK以及8PSK信號經過幅度歸一化后的瞬時幅度譜在±500 kHz（碼速率）處各具有一個很強的沖激。而FSK信號則沒有，其經過幅度歸一化后的瞬時幅度譜如圖2所示。本文根據這兩個沖激之間的寬度提取特征參數T1以區分2FSK信號與BPSK、QPSK、UQPSK、8PSK信號。

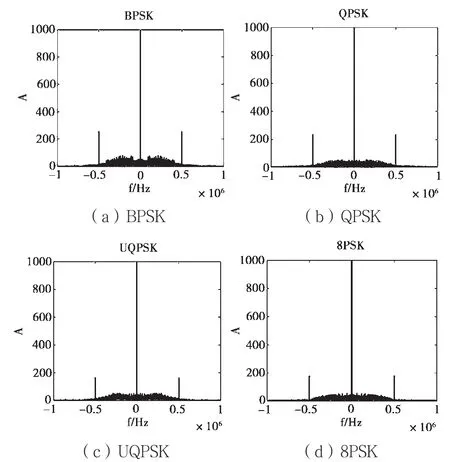
圖1 PSK信號經幅度歸一化后的瞬時幅度譜

圖2 2FSK信號經幅度歸一化后的瞬時幅度譜

1.2 基于信號高階累積量的非線性變換

信號的調制特點不僅反映在信號幅度譜，也反映在信號時域高階累積量上，且信號大于二階的高階累積量可以抑制高斯噪聲的影響[9］。

設復隨機過程s(k)的均值為零，其p階混合矩定義為[9,11］：

其中，s*(k)表示s(k)的共軛，E[?］表示期望。

則s(k)的高階累積量定義為[11］：

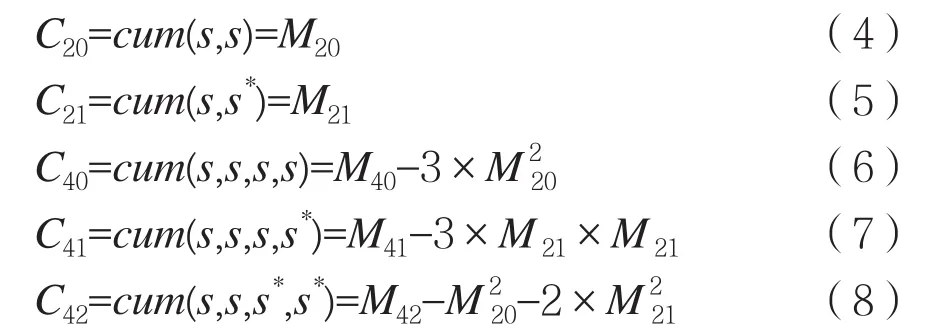
信號四階累積量的理論值如表1所示[11-12］，其中E表示信號能量。

表1 信號四階累積量理論值

在數字信號自動調制識別領域尤其是對MPSK信號的調制識別，信號N次方非線性變換是一種常用的方法[5］。本文根據信號高階累積量以及信號N次方非線性變換[5］提取特征參數：

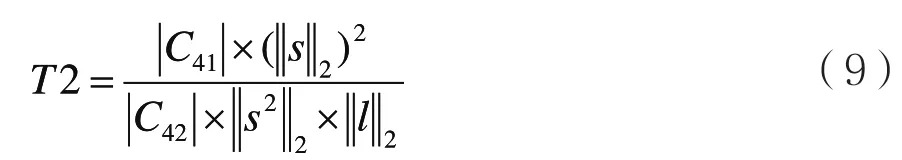
式中，s表示信號，l表示1行n列且元素全為1的向量，n為信號長度，||?||2表示2范數。

以BPSK信號為例對上述特征參數進行理論推導，初相為0的BPSK信號歸一化后的星座圖只有兩個點，（1,0）和（-1,0）且各自占1/2的概率[5］。則BPSK信號T2、T2的理論值計算如下：

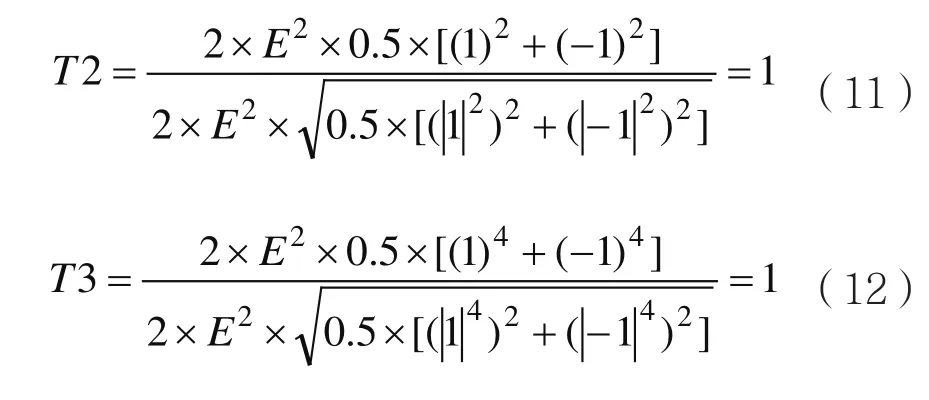
各信號特征參數的理論值如表2所示。其中UQPSK信號的非平衡因子[12］選取為0.3。

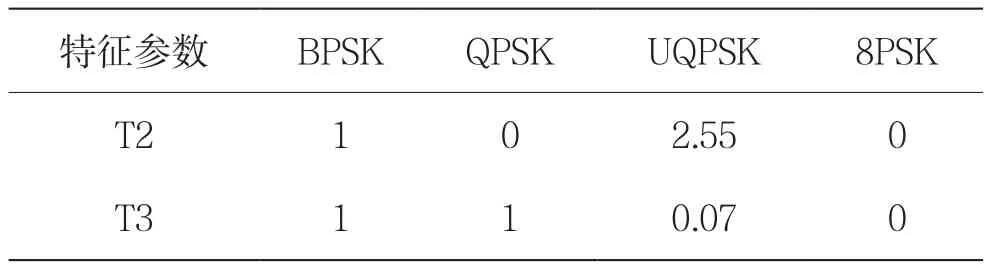
表2 信號特征參數的理論值

2 分類器設計

本文采用經過Sheffield遺傳算法優化的BP神經網絡作為調制識別分類器。BP神經網絡的初始連接權值和閾值對網絡訓練的影響很大，但又無法準確獲得。在使用BP神經網絡時，一般是通過初始化為[-0.5,0.5］區間的隨機數作為網絡的初始權值和閾值[13-14］。經實驗證明這種情況下網絡對于相同的樣本其輸出結果不穩定，因此可以用遺傳算法優化BP網絡的初始權值和閾值,使網絡能更好地進行樣本預測。

本文BP神經網絡采用三層網絡結構，包括輸入層、隱含層、輸出層[14-16］，其結構如圖3所示。網絡的輸入采用列向量輸入，即[T1T2T3］T。輸出采用列向量輸出，總共有5種輸出，每次輸出都是式（13）的一列。第一列代表2FSK信號，第二列代表BPSK信號，以此類推。實際輸出向量的每個元素都在0到1之間，判別信號時在每列中選出最大值置為1，其余元素置為0。

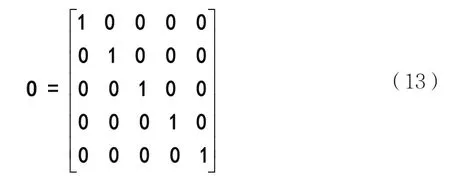
設輸入層神經元個數為n1，隱含層節點數目n2和n1之間有近似關系：

本文對信號提取三個特征參數，因此n1=3，n2=7。網絡輸出層節點數為5，分別對應五種待識別信號。網絡共有3×7+7×5=56個權值，7+5=12個閾值。所以遺傳算法優化的參數個數為68個，包含56個權值和12個閾值。

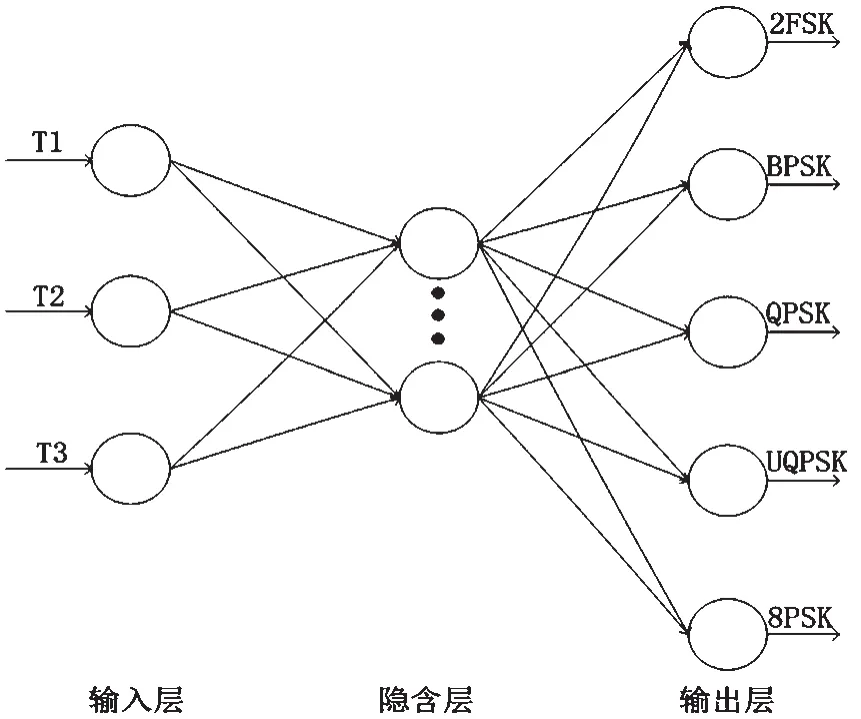
圖3 三層BP神經網絡結構

3 信號識別流程

信號識別算法流程如下：

（1）對信號進行幅度歸一化、中值濾波。

（2）提取特征T1、T2、T3，特征樣本采集。

（3）遺傳算法優化神經網絡。

（4）神經網絡識別信號。

信號識別流程如圖4所示。

4 仿真與結果分析

每個仿真信號長度為7 000個樣點，碼速率為400～600 KBaud，采樣率為4倍碼速率。每種信號在-3～16 dB共生成1 000個特征樣本來訓練BP神經網絡，然后每種信號再在-3～16 dB生成1 000個特征樣本進行測試。信號識別率如圖5所示。

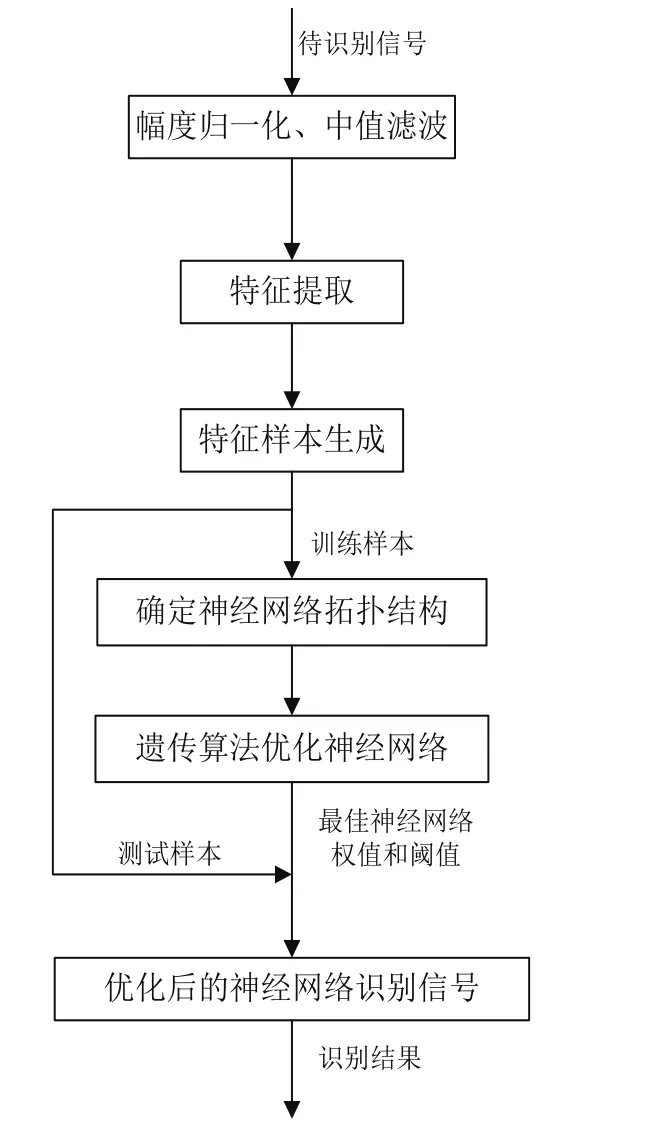
圖4 信號識別流程

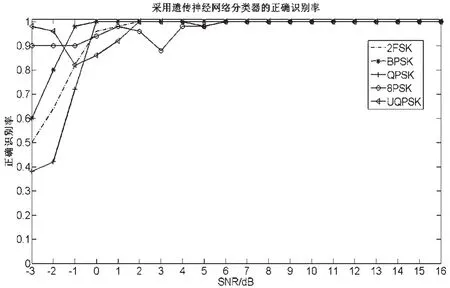
圖5 采用遺傳神經網絡分類器的信號識別率

可見采用本文的方法在低信噪比下對信號具有良好的識別效果。其中對于BPSK、QPSK信號在0 dB時識別率可達96%以上，其余信號在信噪比大于0 dB時信號識別率均能達到85%以上。

在與本文相同的實驗條件下，若采用傳統二叉樹分類器進行信號的識別，其識別率如圖6所示。

由圖6可以看出，采用傳統二叉樹分類器單靠設置的固定門限去區分信號在低信噪比下識別效果不理想。這是因為在低信噪比下，提取的信號特征往往區分不明顯，而本文采用的經遺傳算法優化的BP神經網絡分類器不需要設置固定門限，很好的改善了這一問題，其與采用傳統二叉樹分類器的平均識別率的對比如圖7所示。

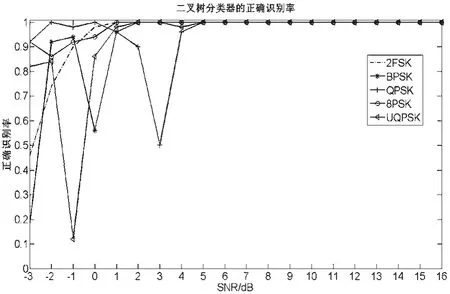
圖6 采用二叉樹分類器的信號識別率

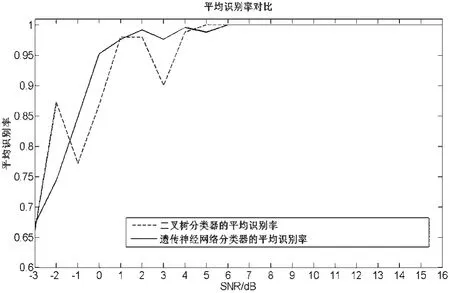
圖7 平均識別率對比

通過圖7可見在本文實驗中采用遺傳算法優化的神經網絡分類器比二叉樹分類器在低信噪比下識別效果更穩定，且在信噪比大于0 dB時平均識別率更高。

5 結 語

為了在低信噪比下有效識別通信信號，提出一種利用遺傳BP神經網絡的信號調制識別新算法。理論分析與實驗結果表明，該算法在低信噪比下對2FSK、BPSK、QPSK、UQPSK、8PSK五種通信中常用的調制信號具有良好的識別效果。且在相同的實驗條件下，采用遺傳算法優化的神經網絡分類器與二叉樹分類器相比在低信噪比下效果更穩定，當信噪比大于0 dB時平均識別率更高。此外，本文提取的特征相較于基于星座圖重構、信號循環譜、壓縮感知理論等提取的特征更易于計算。值得提出的是，采用遺傳算法優化的神經網絡分類器要獲得較好的性能需要大量的訓練樣本，且訓練時間較長，但一旦訓練完成，用于識別信號的速度能達到實時處理信號的要求。后續可通過深度神經網絡進一步改善識別性能。