純電動汽車再生制動控制策略的研究＊

昌誠程 鄭燕萍 王昕燦 馬哲樹

（南京林業大學，南京 210037）

主題詞：純電動汽車 再生制動 制動力分配 控制策略

1 前言

與內燃機汽車不同，純電動汽車可以將制動能量回收再生，從而增加汽車的續駛里程，提高整車性能[1]。目前，再生制動控制策略的研究主要針對理想制動力分配控制策略、制動力按固定比值分配控制策略、最優制動能量回收控制策略和并聯制動能量回收控制策略等4種。如文獻[2]采用理想制動力分配控制策略設計了一種以制動強度和電池SOC為輸入、電機制動比例為輸出的模糊控制器，但這種控制策略會造成驅動輪在低制動強度下獲得的制動力較小，能量回收效率不理想；文獻[3]以固定比值進行前、后輪制動力的分配，基于模糊控制得到機電復合制動下再生制動的比例，希望在保證汽車制動穩定性的基礎上高效地回收制動能量，但這種控制策略存在回收能量不能最大化，而且只能在小于同步附著系數的路面上保證汽車制動的穩定性；文獻[4]在保證驅動輪制動力最大化并滿足ECE法規的條件下完成了前、后輪制動力分配，然后將電池SOC、制動強度和預估的機械制動效能因數引入模糊控制器，得到再生制動分配比例，但這種控制策略同樣只能在部分附著系數路面上保證汽車制動的穩定性。

本文在前人研究的基礎上，提出以路面識別模塊為基礎，在滿足汽車制動法規的前提下，兼顧制動穩定性和制動能量回收效率，將f線（前輪抱死后輪不抱死時前、后輪地面制動力關系曲線）、ECE法規線和I曲線（理想的前后輪制動器制動力分配曲線）相結合，制定汽車前后輪制動力分配曲線，并設計一種三輸入的模糊控制器來分配再生制動的比例。這種再生制動控制策略可以根據不同的路面附著系數動態地調整控制策略，從而在保證汽車制動安全的前提下提高再生制動能量的回收效率。

2 再生制動控制策略

本文將再生制動控制策略分為前后輪制動力分配策略和再生制動分配策略。以高級車輛仿真器ADVISOR中某前輪驅動的純電動汽車為研究對象，其主要參數如表1所列。

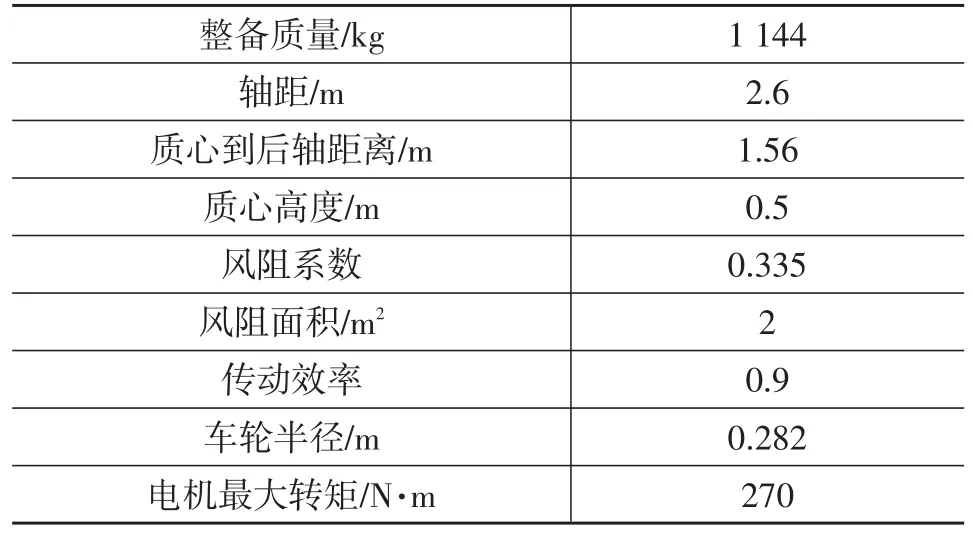
表1 某前輪驅動的純電動汽車主要參數

2.1 前后輪制動力分配策略

2.1.1 路面識別方法

輪胎模型采用Burckhardt等人建立的半經驗模型，該模型以大量的路面試驗數據為基礎[5]，路面附著系數模型表達式為：

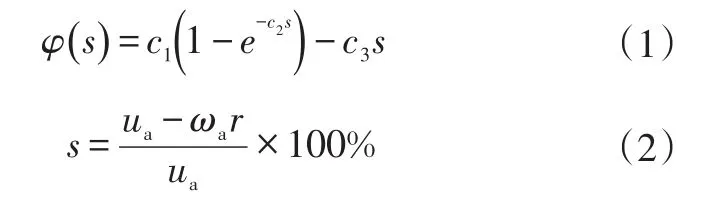
式中，c1、c2、c3為與路面類型相關的常數；s為滑移率；ua為車輪縱向速度；ωa為車輪角速度；r為車輪滾動半徑。

為了能正確地識別路面類型，采用路面狀態特征值τ的概念，并將其作為路面識別參數，其定義為[6]：

式中，φ(s)為制動過程中的制動力系數。

將Burckhardt的數學模型帶入式（3），令滑移率s的積分上限等于最佳滑移率sp，此時τ等于τm，并將τm作為各典型路面特征值的門限值。

由于水泥路面和干瀝青路面特征值的門限值差距較小，因此將這兩種路面合并，得出典型路面的特征值區間，如表2所列。

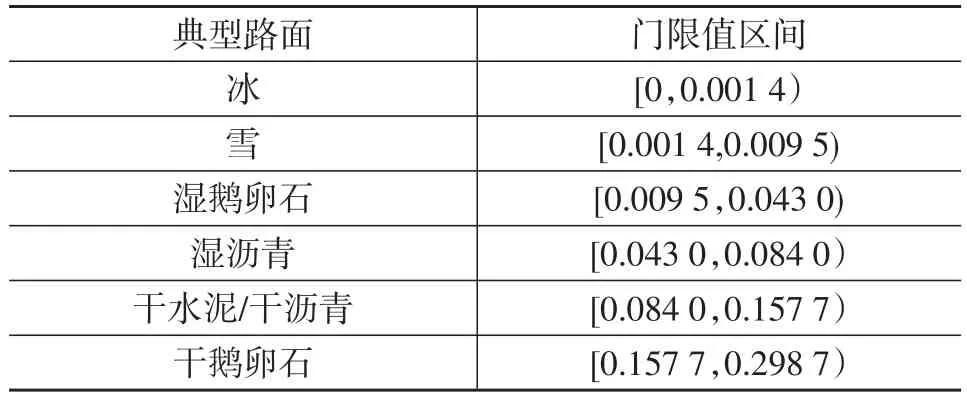
表2 典型路面特征值區間

2.1.2 前后輪制動力分配曲線設計

根據汽車理論，所設計的前、后輪制動力分配曲線由ECE制動安全法規線、f線和I曲線組合而成[7]，并根據當前路面的附著系數選擇不同的控制策略，使前輪在獲得較大制動力的同時確保制動的方向穩定性。

制動力分配策略方案如下：利用車型參數求出ECE法規與橫軸的交點，此點對應的汽車前輪制動力為2 412.72 N，后輪制動力為0，此刻對應的路面附著系數φ0=0.335 5。為保證制動時前輪不抱死，確定臨界的路面附著系數為φx，根據公式φx=φ0/0.85計算得φx=0.394 7，將φx對應的f線稱為fx線。

根據臨界附著系數，將路面附著情況分為小路面附著系數情況和大路面附著系數情況，并分別設計了前、后輪制動力分配曲線，分配策略如下。

a.小路面附著系數情況（φ≤φx）。圖1為路面附著系數φ＜φx時的制動力分配曲線（假設當前路面附著系數φ=0.3），曲線OABC為前、后輪制動力分配曲線，并且隨路面附著系數變化而變化，線段AB是將當前路面附著系數φ所對應的f線組左移后得到的，且線段AB的前輪制動力是f線制動力的85%，線段OC是I曲線。

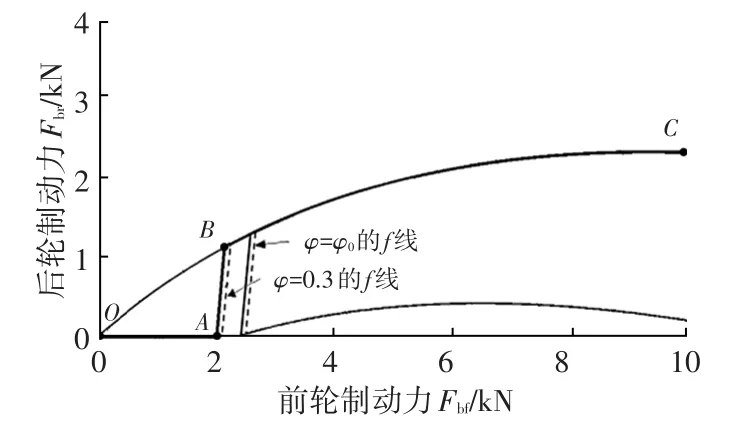
圖1 小路面附著系數下的的前后輪制動力分配曲線

路面附著系數φ≤φx時的前輪制動力分配曲線方程為：

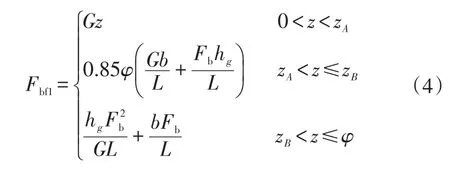
式中，Fbf1為φ≤φx時的前輪制動力；zA、zB分別為A、B點所對應的制動強度，z為當前制動狀態下的制動強度；G為整車整備質量；φ為路面附著系數；b為質心到后軸距離；hg為質心高度；L為軸距；Fb為總制動力。

b.大路面附著系數情況（φ＞φx）。圖2為路面附著系數φ＞φx時的制動力分配曲線（設當前路面附著系數φ=0.7），曲線ODEFG為前、后輪制動力分配曲線，線段DE是ECE法規線，線段EF同樣是當前路面附著系數φ所對應的f線左移后得到的，線段OG是I曲線。

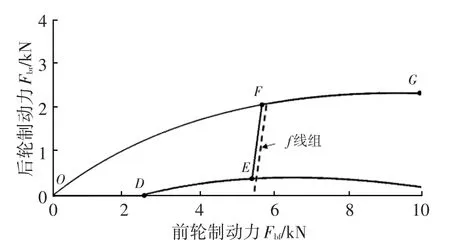
圖2 大附著系數情況前后輪制動力分配曲線

路面附著系數φ＞φx時的前輪制動力分配曲線方程為：

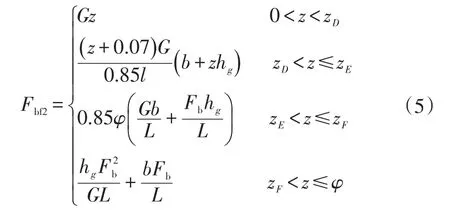
式中，Fbf2為φ＞φx時的前輪制動力；zD、zE、zF分別為D、E、F點對應的制動強度。

2.2 基于模糊控制的再生制動分配策略

將實時的制動強度z、電池SOC和車輛速度V作為模糊控制器的輸入，再生制動占前輪總制動力的比例k作為模糊控制器的輸出[8]。制動強度z的隸屬度函數如圖3所示，制動強度z的取值為[0,1],當z較低時，應盡量采取再生制動方式；當z較高時，汽車處于緊急制動狀態，此時應采用摩擦制動方式。隸屬度函數使用梯形函數，模糊語言變量為非常低、低、中等、高和非常高，制動強度z的模糊集設置為{VL,LO,MI,HI,VH}。

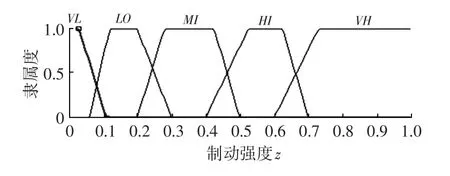
圖3 制動強度z隸屬度函數

電池SOC的取值為[0,1]，且SOC較小時應增加再生制動比例，保證車輛的正常行駛；當電池SOC較高時，為了延長電池壽命，應減小再生制動比例。電池SOC隸屬度函數取鐘型和高斯型，如圖4所示，其模糊語言變量為非常低、低、中等、高和非常高，故其模糊集為{VL,LO,MI,HI,VH}。

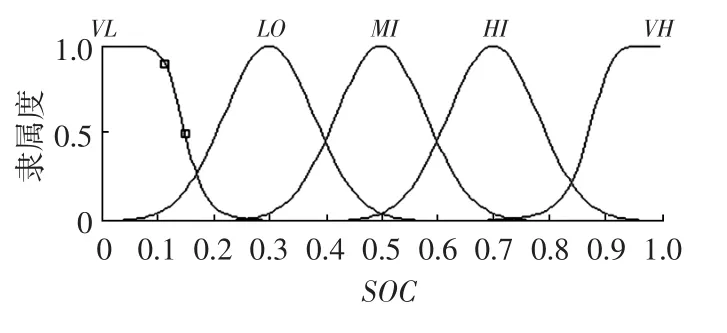
圖4 電池SOC隸屬度函數

本文采用的汽車最高車速為111 km/h，取值范圍為[0,111]。當車速小于10 km/h時，電機轉速較低，制動能量回收能力較弱，因此采用較低的再生制動比例[9]；當車速大于10 km/h時，再生制動比例由制動強度z和電池SOC決定。車速隸屬度函數取梯形函數，如圖5所示，其模糊語言變量為低和高，模糊集設置為{LO,HI}。

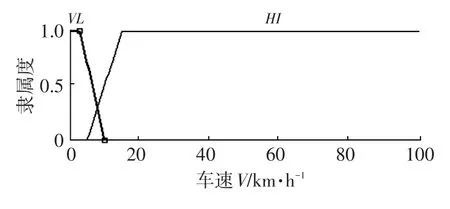
圖5 車速隸屬度函數

再生制動比例k隸屬度函數采用梯形函數，如圖6所示。k取值為[0,1]，其模糊語言變量為非常低、低、中等、高、非常高，將模糊集設置為{VL,LO,MI,HI,VH}。

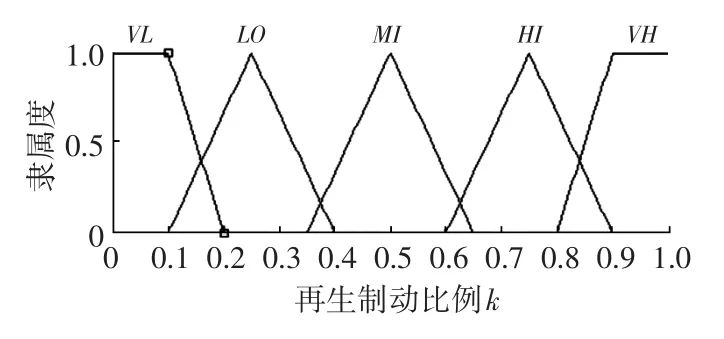
圖6 再生制動比例k隸屬度函數

根據隸屬度函數的分析和仿真研究，設計的模糊控制器規則庫如表3所列。

3 仿真分析

利用矩陣實驗室MATLAB中的Simulink工具搭建了控制策略模型，將其鑲嵌到ADVISOR中進行二次開發，選取日本CYC_1015和美國CYC_UDDS[10-11]兩種循環行駛工況進行模擬仿真，并與ADVISOR原控制策略進行對比。

3.1 仿真模型建立

在路面識別模塊中，輸入為地面制動力、車輪的垂直載荷和滑移率，輸出為典型路面的平均附著系數。圖7為再生制動控制策略的前、后輪制動力分配和再生制動分配仿真模塊，模塊的輸入是需求總制動力Fb，根據當前路面附著系數和制動強度，選取前、后輪制動力分配曲線，再根據輸入Fb計算前、后輪的總制動力Fbf和Fbr。因為車輛為前輪驅動，所以后輪總制動力即為后輪摩擦制動力，而前輪再生制動力需要由模糊控制器根據制動強度z、車速V和SOC計算出的前輪再生制動比例k與前輪總制動力相乘得出，再將前輪總制動力減去再生制動力得到前輪摩擦制動力，最后將前輪摩擦制動力和后輪摩擦制動力輸出給上層模塊。

表3 模糊控制規則

3.2 仿真結果分析

在CYC_1015和CYC_UDDS工況下，控制策略優化前、后電池SOC隨時間變化曲線如圖8所示。由圖8可看出，利用優化后控制策略仿真得到的電池SOC變化曲線相比原控制策略仿真得到的曲線下降緩慢，并且曲線數值較高，這表明所設計的控制策略能夠回收更多的能量。

在CYC_1015和CYC_UDDS工況下，控制策略優化前、后純電動汽車電機輸出轉矩如圖9所示。從圖9可以看出，當轉矩為正時（電動機處于驅動狀態，消耗電池能量），兩種控制策略下的仿真曲線重合，說明純電動汽車獲得的驅動力大小相等；當轉矩為負時（電機處在再生制動狀態，向電池輸入電能）,優化后控制策略所得仿真曲線峰值的絕對值較大，表明電機回收了更多的制動能量給電池。

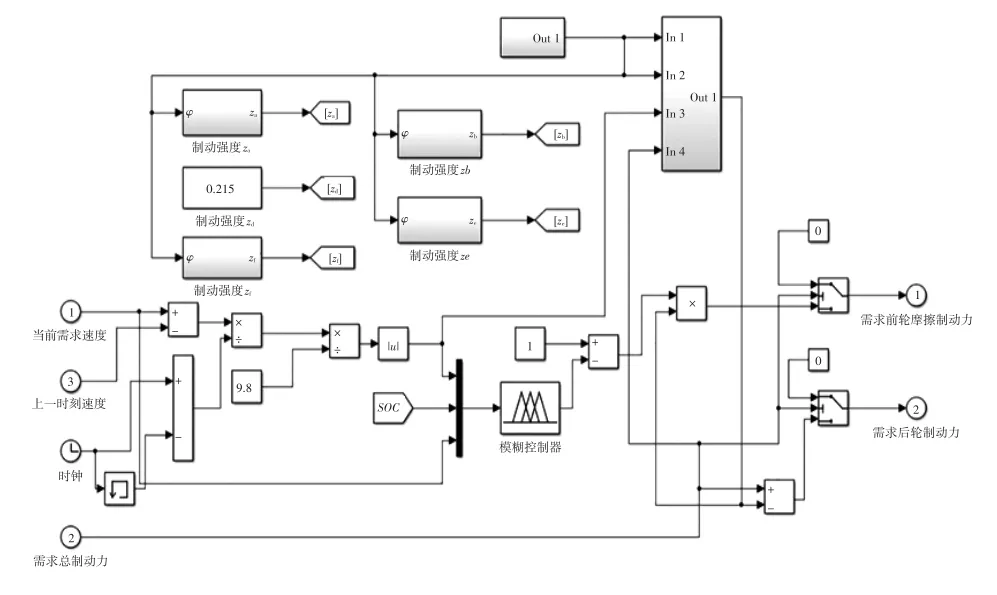
圖7 需求再生制動力模塊

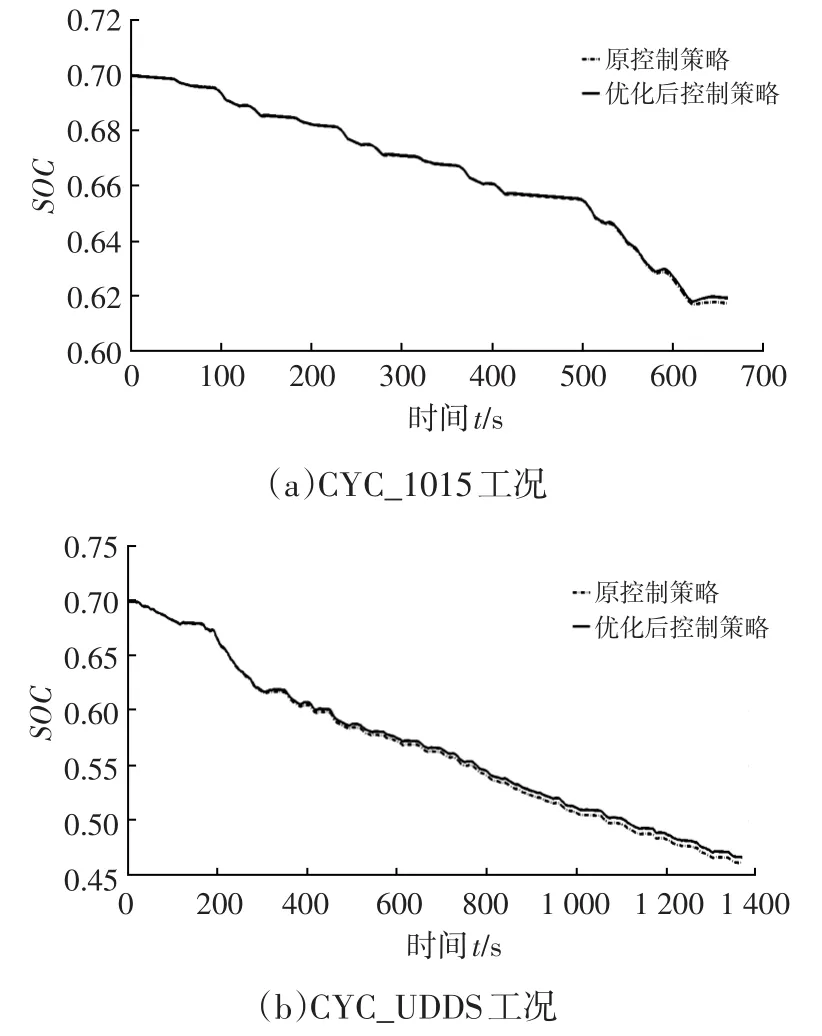
圖8 兩種工況下控制策略優化前、后電池SOC變化曲線

為客觀地評價所設計控制策略的能量回收效果，利用制動能量回收率ηb和有效制動能量回收率ηeb兩個評價指標進行分析：

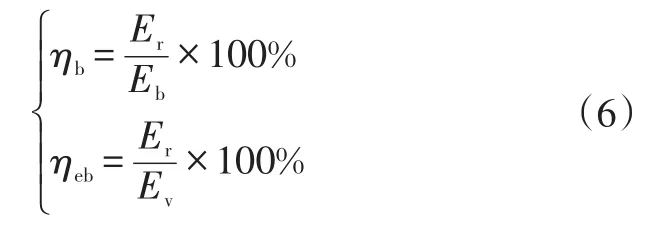
式中，Er為電池回收的能量；Eb為制動總能量；Ev為整車能量損耗。

ηb和ηeb的計算結果如表4和表5所示。由表4和表5可知，在CYC_1015工況和CYC_UDDS工況下，ADVISOR原控制策略的SOC值都小于優化后控制策略的SOC值，并且在優化后的控制策略下，電池通過再生制動回收的能量都大于原控制策略下回收的能量，有效制動能量回收率也相對較大，說明優化后控制策略比ADVISOR原控制策略能更好地回收制動能量，提高了純電動汽車的續駛里程。

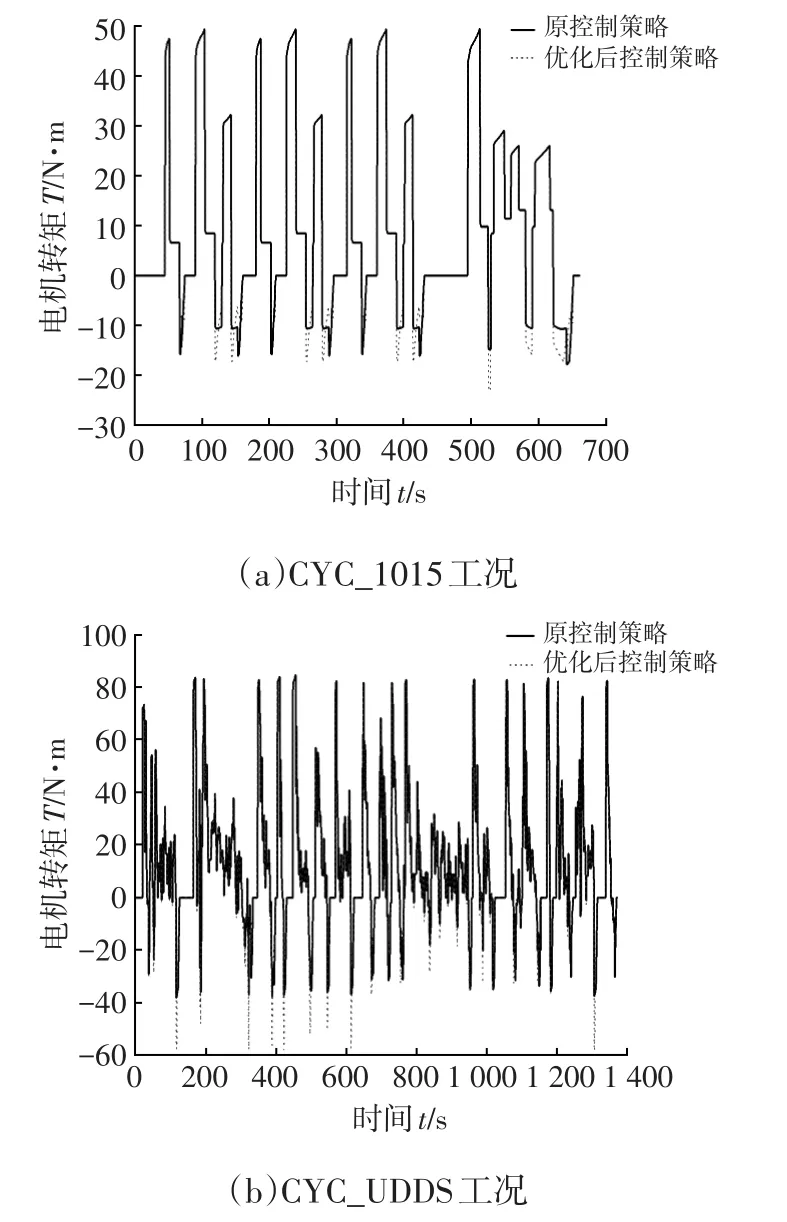
圖9 兩種工況下控制策略優化前、后電機轉矩

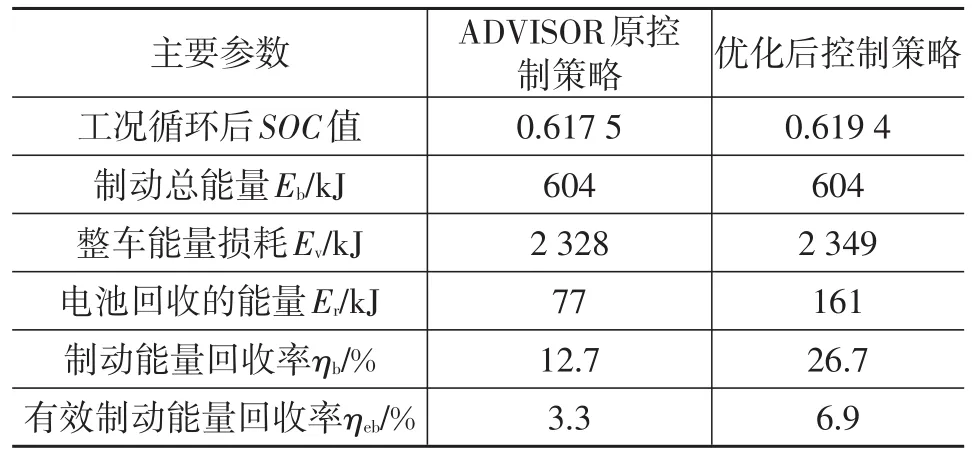
表4 CYC_1015工況下控制策略優化前、后制動能量對比

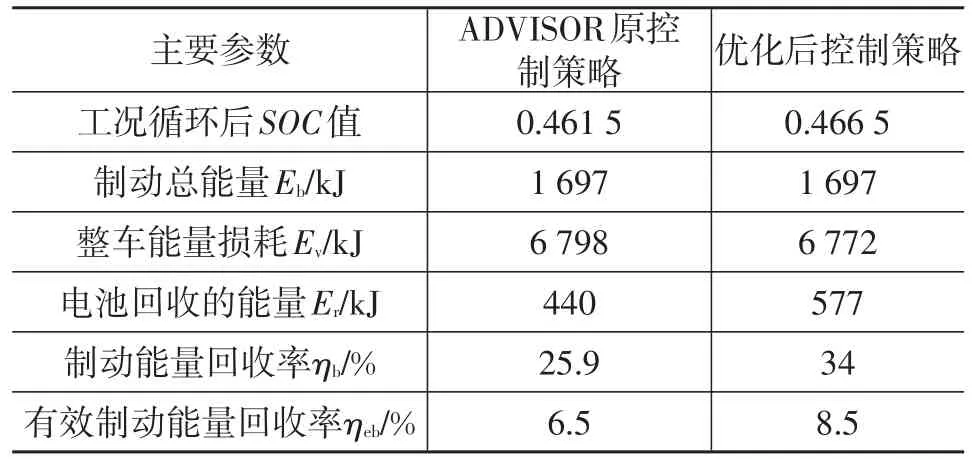
表5 CYC_UDDS工況下控制策略優化前、后制動能量對比

4 結束語

以某純電動汽車再生制動系統為研究對象，提出了基于模糊控制器的再生制動控制策略，這種控制策略是以路面識別為前提，實時地進行再生制動控制策略的調整，能夠在保證汽車行駛安全的前提下，提高制動能量的回收效率，從而提高純電動汽車的續駛里程。以ADVISOR為平臺，建立了控制策略的仿真模型，在日本CYC_1015和美國CYC_UDDS兩種循環行駛工況下進行了仿真測試，將仿真結果與ADVISOR原控制策略進行了對比，驗證了所設計控制策略的有效性。