一種改進的非支配排序遺傳算法

王青松，謝興生，周光臨

(中國科學技術大學 信息科學技術學院，安徽 合肥 230026)

0 引言

在實際生活以及工程應用中，經常要求在給定的資源下，同時滿足多個目標最優化，即多目標優化[1]。比如在部署虛擬機時，需要同時滿足高利用率、低延遲以及高吞吐量等[2]；在交通信號配時中，需同時使得延誤時間最小、通行能力最大以及停車次數最少[3]。對于多目標優化問題，傳統的處理方法大多是加權法，即通過對不同的優化目標分配不同的權重，把多目標優化問題轉化為單目標優化問題來求解。加權法的缺點主要有兩點，一方面權重的設置具有主觀性，需要對優化問題有充分的了解；另外一方面，優化目標之間通常不是線性相關的，因此求得的解通常來說不是全局最優解。對于多目標優化問題，由于幾乎不存在單個全局最優解，因此通常是求解一系列非支配解[4](Pareto解集)。

非支配排序遺傳算法[5](Non-dominated Sorting Genetic Algorithm II，NSGA-II)是DEB K等人提出的一種元啟發式算法，由于NSGA-II算法在低維優化問題中表現優良，并且算法實現相對容易，因此被廣泛使用。比如李曉青等人[6]針對發電功率，對風力發電子系統和光伏發電子系統一起使用NSGA-II算法進行協調控制，使得風能和太陽能更為合理地得到利用；AHMADI V等人[7]使用NSGA-II算法求解(Software Defined Network,SDN)體系結構中的控制器的部署位置，顯著提高了網絡的負載均衡能力、可靠性和容錯性。然而，NSGA-II算法在求解時更關注解集質量，求出的解集在分布性方面相對較差。針對NSGA-II算法的不足，本文提出了一種改進的非支配排序遺傳算法(INSGA-II)。

本文首先擴大了NSGA-II算法初始化種群規模，其目的是提高收斂性，然后為了提高解集的分布性，引入了概率選擇算子。同時為了增大算法的搜索空間，提出了混合交叉算子。最后使用公開的多目標測試函數，以世代距離(Generational Distance，GD)、分布性(Δ)和反世代距離(Inverted Generational Distance，IGD)作為性能指標[8]，與NSGA-II算法和改進的多目標粒子群算法[9](Optimized Multi-Objective Particle Swarm Optimization，OMOPSO)算法進行比較。

1 NSGA-II算法相關概念

NSGA-II算法主要有三大核心概念：快速非支配排序、擁擠距離以及精英策略。

1.1 快速非支配排序

快速非支配排序算法根據種群中個體的優劣程度來對種群分層，目的是使得下一步搜索方向往Pareto最優解集靠近。令nt為支配個體t的個體數目，st為被個體t支配的所有個體，則具體步驟如下：

(1)把種群中滿足nt=0的所有個體存入到當前非支配集合F1中。

(2)被F1中的個體i支配的個體集合記為Si。遍歷集合Si，對于其中的每個個體l，將其支配數nl更新為nl-1，若nl=0，則把個體l保存到新的集合H中。

(3)此時，F1集合為第一級非支配個體集合，里面所有個體的非支配序均相同，而集合H重新作為當前非支配集合，重復上述步驟，直到所有個體均被賦予了非支配序。

1.2 擁擠距離

擁擠距離刻畫了種群中個體的分散程度，令Ci為個體i的擁擠距離，則在邊緣上的個體的擁擠距離為∞，其余個體的擁擠距離計算公式如下：

(1)

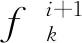
i>cj?irankCj

(2)

式中，irank表示個體i的非支配序。式(2)含義為個體i優于個體j，當且僅當個體i的非支配序小于個體j的非支配序或者個體i的非支配序等于個體j的非支配序且個體i的擁擠距離大于個體j的擁擠距離。

1.3 精英策略

精英策略的目的是避免優秀的Pareto解集丟失。首先將父代種群Pt和子代種群Qt組合成大小為2N的新種群Rt，然后對集合Rt進行快速非支配排序和擁擠距離計算，并按照非支配序從低到高排序，選擇個體進入新種群Pt+1中，如果某個相同非支配序集合中的個體全部加入Pt+1超過了種群上限值N，則此時按照擁擠距離從該集合中進行優選，直到種群數量為N。

2 改進的NSGA-II算法

為了提高NSGA-II算法的收斂性和分布性，以獲得更多和更好的解，提出以下三種改進策略。

2.1 新的初始化種群

在NSGA-II算法中，初始化種群P0是隨機產生的，且種群的大小為N，而子代種群Q0則是基于種群P0經過選擇、交叉和變異產生的。算法進行第一次迭代時，可以視為隨機搜索。對于隨機搜索，顯然種群個體越多，找到最優解的概率就越大，但是個體也不能無限增加，否則可能會影響算法的收斂時間。在不影響算法復雜度的前提下，若種群個體為N，初始化種群的個體數目可以設置為1.5N～2N之間，其目的是提高第一輪子代種群Q0的質量，加速整個種群往最優解靠近。

2.2 概率選擇算子

選擇算子是算法的核心算子之一，作用是從當前種群中選擇出優良的個體并用于后續交叉、變異以產生新的子代種群，它決定了當前種群的下一步走向。NSGA-II算法選擇算子常采用的策略是二元錦標賽選擇，即隨機從種群中選擇兩個個體，讓這兩個個體互相比較，選擇出最優個體，比較的策略是基于個體的非支配序和擁擠距離。由于選擇算子對于算法的性能至關重要，因此選擇算子的好壞會影響到所求的解集的質量。

NSGA-II的選擇算子更關注解的質量，為了讓選擇算子在保證解的質量前提下提高所求解集的分布性，在原有的選擇算子基礎之上引入了概率操作。在種群進化初期，以較大的概率拒絕當前選出的最優個體，選擇另外的個體，保證了算法初期的種群多樣性，在進化后期，由于種群趨向于收斂，因此以較小的概率拒絕當前選出的最優個體，但是仍然保留選擇另外個體的可能性。概率操作的計算公式為：

(3)

式中，w為概率選擇算子參數，g為進化代數。

2.3 混合交叉算子

基本的NSGA-II算法中對實數編碼采用了模擬二進制交叉(Simulated Binary Crossover，SBX)，SBX交叉算子實現起來比較簡單，但是移動空間的范圍比較小，因此搜索能力相對較弱，容易陷入局部最優解。針對SBX交叉算子存在的缺點，提出了混合交叉算子，即在SBX交叉算子基礎上引入高斯分布交叉算子(Normal Distribution Crossover，NDX)，并自適應地調整這兩種交叉算子權重。NDX交叉算子相對于SBX交叉算子的優勢在于搜索空間更大，因此更容易跳出局部最優[10]。在算法初期，由于種群中的個體不知道最優解位于何處，因此應該加大搜索空間范圍，讓NDX交叉算子的權重更大。在算法迭代的后期，由于整個種群已經趨向于穩定，大部分個體都在最優Pareto解周圍，因此可以縮小搜索空間，此時讓SBX交叉算子權重變大，以加速算法收斂。令u為區間(0,1)上均勻分布所產生的隨機數，r=|N(0,1)|為高斯分布隨機變量的值，則當u≤0.5時，個體在混合交叉算子下的更新公式為：

(4)

當u>0.5時，個體在混合交叉算子下的更新公式為：

(5)

式(5)、(6)中，x1,i和x2,i為混合交叉算子產生子代個體第i個變量的值；M=p1,i+p2,i，N=p1,i-p2,i，p1,i和p2,i為父代個體第i個變量的值；g為當前迭代次數，G為總的迭代次數，ηc為交叉算子參數。

2.4 INSGA-II算法步驟

INSGA-II算法步驟如下：

(1)設置算法參數:種群規模N，初始化種群P0的規模N0=1.5N～2N，迭代次數G，概率選擇算子參數w以及混合交叉算子參數ηc。

(2)隨機產生N0個個體作為父代種群P0。

(3)當前迭代次數g=0，對父代種群P0進行概率選擇、混合交叉和變異操作，生成子代種群Q0。

(4)合并父子代種群Pt和Qt為新種群Rt，對新種群Rt進行快速非支配排序。

(5)使用精英策略，從新種群Rt中選擇出N個優良個體作為新的父代種群Pt+1。

(6)對新種群Pt+1進行概率選擇、混合交叉和變異操作，生成新子代種群Qt+1。

(7)若當前迭代次數g不小于最大迭代次數G，則算法結束，否則g=g+1，并進入步驟(4)。

3 實驗與分析

3.1 測試函數和參數設置

為了評估INSGA-II優化算法的有效性，使用四個公開的標準多目標測試函數來進行測試，分別是ZDT1、ZDT2、ZDT3和ZDT4函數[11]，具體表達式如公式(6)～公式(9)所示。為了公平且合理比較不同的多目標優化算法，種群規模的大小均設置為100，最大迭代次數均設置為1 000；NSGA-II算法和INSGA-II算法的變異算子參數以及交叉算子參數均為20，INSGA-II概率選擇算子中的w參數設置為0.01；OMOPSO算法的變異概率為1/d，d為變量個數，存檔的大小為100，慣性量權重系數W的值為random(0.1,0.5)；真實Pareto前沿的采樣點個數為500。同時為了提高評價結果的穩定性，對每個測試函數使用優化算法重復求解50次，計算不同評價指標的平均值。

(6)

(7)

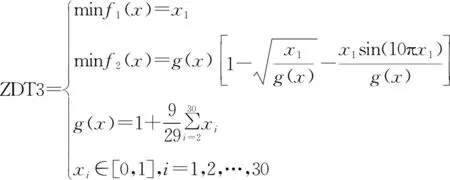
(8)

(9)

對于三個評價指標，收斂性評價指標GD的計算公式如下：

(10)

式中，di表示算法求解得到的Pareto前沿PF中的個體i和真實Pareto前沿集合的最短距離，值越小，表明解集質量越高。分布性評價指標SP的計算公式為：

(11)

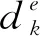
(12)

式中，d(x,y)表示點x與點y之間的距離，IGD值越小，表明所求的最優解集組成的Pareto前沿PF越逼近真實的Pareto前沿PF*，算法的綜合性能越好。

3.2 結果和分析

三種優化算法對四個測試函數求解得到的Pareto前沿的局部放大結果如圖1～圖4所示，其性能指標結果如表1所示。由圖1到圖4可以看出，INSGA-II算法能比較接近真實的Pareto前沿。從表1中的數據可知，INSGA-II算法在大多數情況下收斂性和分布性比NSGA-II算法要好，在ZDT1和ZDT3測試函數上，INSGA-II算法的GD略低于OMOPSO算法，但是INSGA-II算法的分布性卻大大優于OMOPSO算法。相比于OMOPSO算法，INSGA-II算法在保證Pareto解集質量的前提下，同時保證了Pareto解集的分布性。這表明新的初始化種群、概率選擇算子以及混合交叉算子有效地改善了NSGA-II算法的分布性和收斂性。

圖1 ZDT1函數實驗結果局部放大

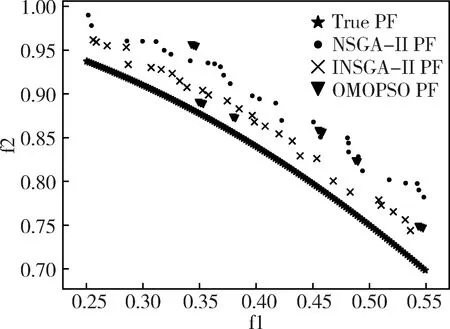
圖2 ZDT2函數實驗結果局部放大

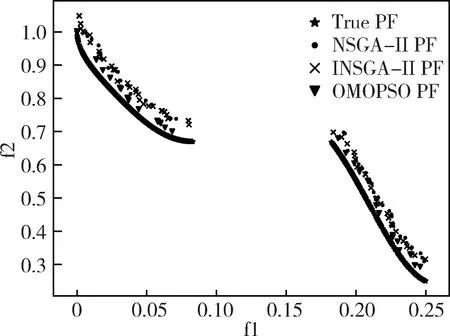
圖3 ZDT3函數實驗結果局部放大

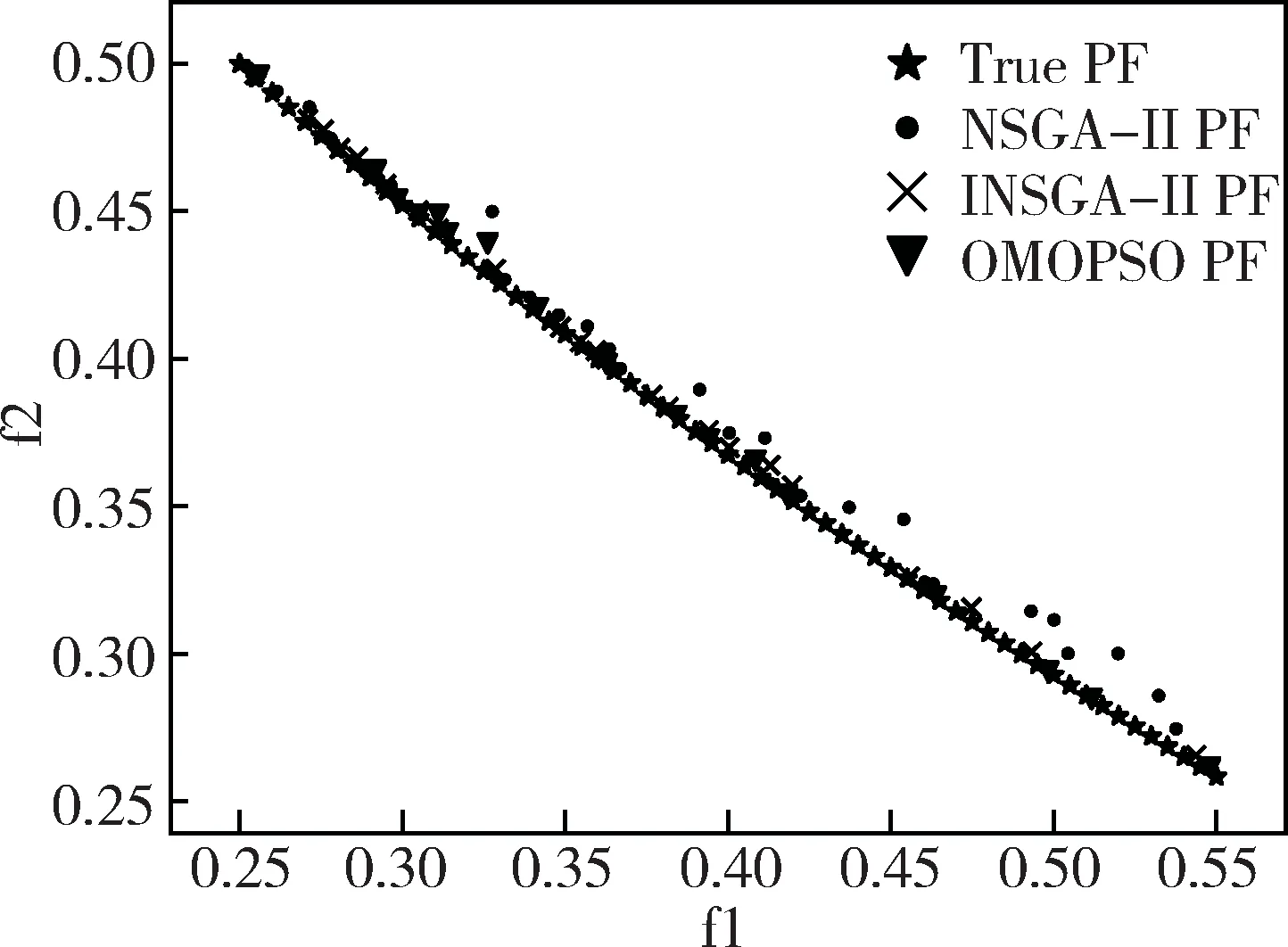
圖4 ZDT4函數實驗結果局部放大

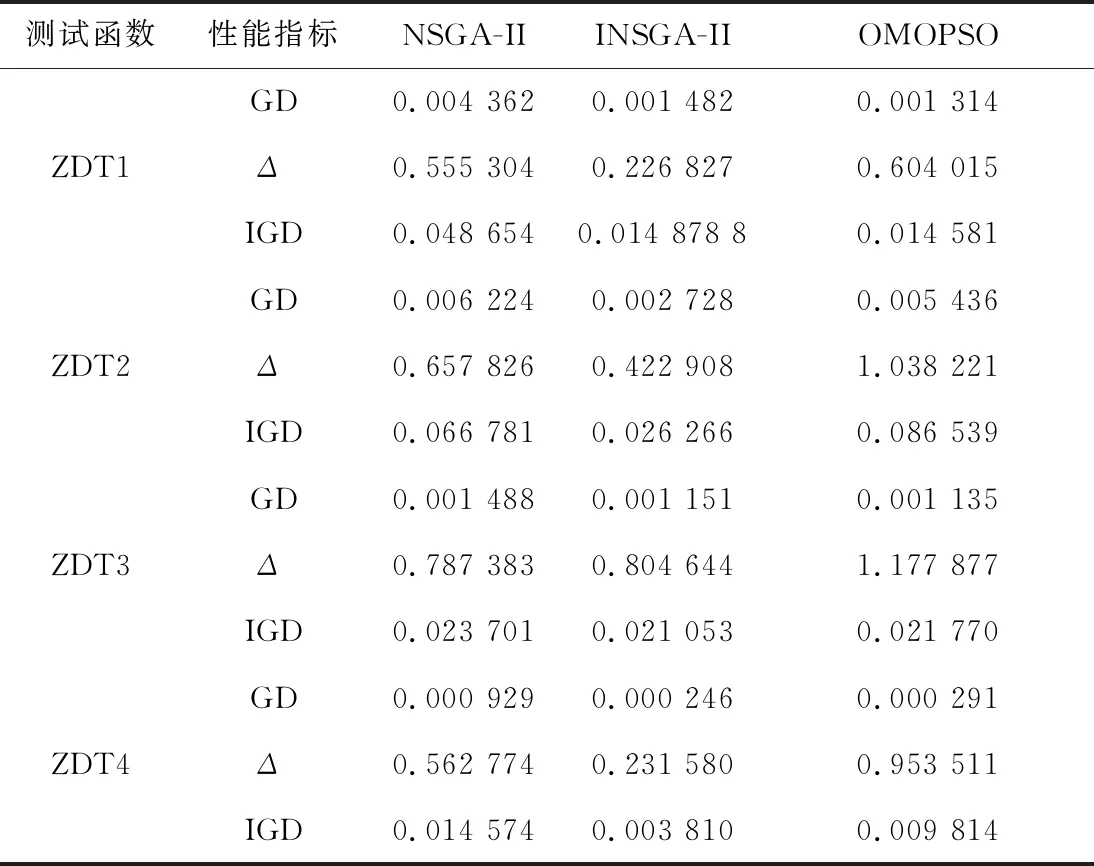
測試函數性能指標NSGA-IIINSGA-IIOMOPSOGD0.004 3620.001 4820.001 314ZDT1Δ0.555 3040.226 8270.604 015IGD0.048 6540.014 878 80.014 581GD0.006 2240.002 7280.005 436ZDT2Δ0.657 8260.422 9081.038 221IGD0.066 7810.026 2660.086 539GD0.001 4880.001 1510.001 135ZDT3Δ0.787 3830.804 6441.177 877IGD0.023 7010.021 0530.021 770GD0.000 9290.000 2460.000 291ZDT4Δ0.562 7740.231 5800.953 511IGD0.014 5740.003 8100.009 814

4 結論

本文提出了一種改進的非支配排序遺傳算法，通過擴大初始化種群規模，來加速算法收斂；對選擇算子引入概率操作，提高了種群的多樣性；同時為了擴大算法的搜索空間，引入了混合交叉算子。最后，使用公開的多目標基準函數進行測試，并和基本的NSGA-II算法以及OMOPSO算法進行對比，驗證了本文提出的INSGA-II算法能獲得分布性和收斂性更好的Pareto前沿。未來的工作將考慮使用更復雜的公開測試函數來對INSGA-II算法進行測試，并在交通信號配時優化等實際工程問題中檢驗INSGA-II算法的性能。