乘積G-空間的G-極小性、G-混合性和G-鏈回歸點

冀占江,張更容

(1.梧州學院大數據與軟件工程學院,廣西梧州 543002)

(2.梧州學院廣西高校圖像處理與智能信息系統重點實驗室,廣西梧州 543002)

(3.湖南第一師范學院數學與計算科學學院,湖南長沙 410205)

1 引言

極小性和混合性是拓撲動力系統中重要的概念,其核心是迭代所產生的系列軌道在拓撲空間中的漸進性和拓撲結構,近年來許多學者對其進行了研究,得到了很多有意義的成果(見文獻[1–7]).例如,文獻[1]證明了在緊致度量空間中極小性和拓撲混合可以被強一致收斂所保持;文獻[2]給出了圖上交錯系統中拓撲混合的等價條件;文獻[3]給出了樹映射是拓撲混合的等價條件;文獻[4]證明了乘積映射是極小映射和混合映射相應等價于分映射是極小映射和混合映射.文獻[1–4]是在整數加群Z作用下的拓撲空間上研究極小性和拓撲混合,也就是在經典離散動力系統中研究極小性和拓撲混合,隨著離散系統動力系統中理論的成熟,在一般群作用下的拓撲空間中的動力學性質逐漸受到學者的關注[8?11].文獻[8]在Amenable群作用下研究了極小性和拓撲混合的等價條件;文獻[9]在拓撲群中下證明了拓撲混合可以被強一致收斂所保持.我們知道整數加群Z一定是Amenable群和拓撲群,反之不一定成立,因此文獻[8–11]所研究的空間比離散動力系統更為廣泛,結論更具有實用性和普遍性.借鑒文獻[8–11]的研究思路,筆者在拓撲群作用下的乘積空間中進行研究,首先介紹了極小映射和混合映射的概念,其次證明了(1)乘積映射f×g是G-極小映射當且僅當是f是G1-極小映射,g是G2-極小映射;(2)乘積映射f×g是G-混合映射當且僅當是f是G1-混合映射,g是G2-混合映射.另外鏈回歸點也是動力系統中十分重要的概念,近年來也取得了有意義的研究成果[12?14].文獻[12]證明了在緊致度空間中,若映射f具有偽軌跟蹤性,則文獻[13]證明了在緊致度空間中,若映射f具有周期偽軌跟蹤性,則文獻[14]在拓撲群作用下的逆極限空間中研究了鏈回歸點,指出移位映射的鏈回歸點集等于自映射在其鏈回歸點集上形成的逆極限空間.筆者在拓撲群作用下的乘積空間中研究了鏈回歸點的拓撲結構,證明了CRG(f×g)=CRG1(f)×CRG2(g).這些結果彌補了拓撲群作用下乘積空間中極小映射、混合映射和鏈回歸點理論的缺失,為它們在今后的應用中提供了理論依據和科學基礎.

2 基本概念及記號

定義2.1[15]設X是度量空間,G是拓撲群.若映射?:G×X?→X滿足

(1)對任意的x∈X,有?(e,x)=x,其中e為G的單位元;

(2)對任意的x∈X 以及g1,g2∈G,有?(g1,?(g2,x))=?(g1g2,x),則稱(X,G,?)是度量G-空間,簡稱X 是度量G-空間.為了書寫方便,通常將?(gx)簡寫為gx.

下面給出乘積度量G-空間的概念.

定義2.2設(X,d1)是度量G1-空間,(Y,d2)是度量G2-空間,在乘積空間X×Y上定義d((x1,y1),(x2,y2))=max{d1(x1,x2),d2(y1,y2)},則稱d是乘積空間X×Y上的度量.

設f:X?→X 連續,g:Y?→Y連續,定義(f×g)(x,y)=(f(x),g(y)),則稱f×g是f與g的乘積映射.

取G=G1×G2,易知G是拓撲群,(X×Y,d,G)是度量G-空間,此時稱(X×Y,d,G)是(X,d1,G1)和(Y,d2,G2)的乘積度量G-空間.

定義2.3[14]設(X,d)是度量G-空間,f:X ?→X 連續,x∈X,稱x是f的G-鏈回歸點,如果?ε>0,?f作用下的(G,ε)鏈其中x0=xn=x.f的G-鏈回歸點集用CRG(f)表示．

定義2.4[9]設(X,d)是度量G-空間,f:X ?→X 連續,稱f是G-混合映射,如果對X 任意非空開集U和V,存在正整數m,存在p∈G,當n>m時,有pfn(U)TV 6=?.

定義2.5設(X,d)是度量G-空間,f:X ?→X 連續,x∈X,稱orbG(x,f)為f作用下的G-軌道,如果記orbG(x,f)≡{pfn(x):p∈G,n≥0}.

定義2.6設(X,d)是度量G-空間,f:X ?→X 連續,稱f是G-極小映射,如果對任意的x∈X,有

3 主要定理

定理3.1設(X,d1)是度量G1-空間,(Y,d2)是度量G2-空間,f:X ?→X 連續,g:Y?→Y連續,則f×g是G-極小映射當且僅當是f是G1-極小映射,g是G2-極小映射.

證? 假設f×g是G-極小映射.?x∈X，?y∈Y,取z=(x,y),則z∈X ×Y.由f×g是G-極小映射知

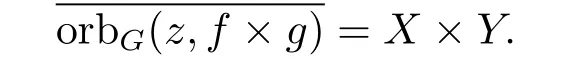
設U是X上的任意非空開集,V是Y上的任意非空開集,則U×V是X×Y上的非空開

集,故

又

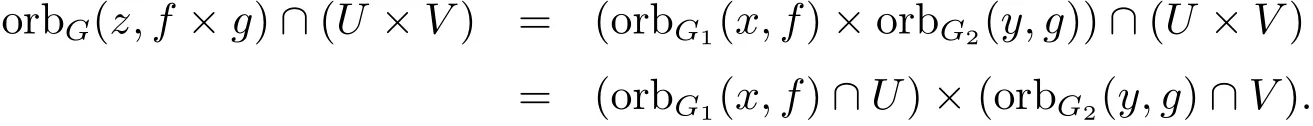
故

則

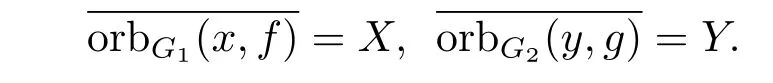
因此f是G1-極小映射,g是G2-極小映射.

? 假設f是G1-極小映射,g是G2-極小映射.設U0×V0是X×Y上的任意非空開集,則U0是X 上的非空開集,V0是Y 上的非空開集,?z0=(x0,y0)∈X×Y,則x0∈X,y0∈Y,由f是G1-極小映射和g是G2-極小映射知

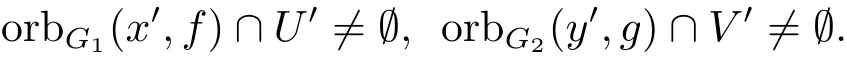
又

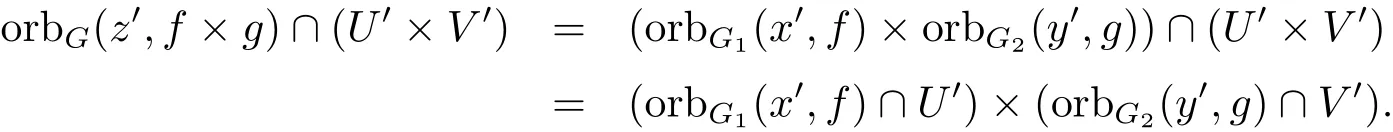
故

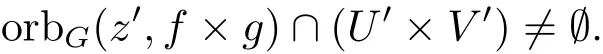
則

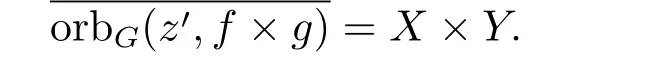
因此f×g是G-極小映射.

定理3.2設(X,d1)是度量G1-空間,(Y,d2)是度量G2-空間,f:X ?→X 連續,g:Y?→Y連續,則f×g是G-混合映射當且僅當是f是G1-混合映射,g是G2-混合映射.

證 ? 假設f×g是G-混合映射.?X 上的任意非空開集U1和V1,?Y上的任意非空開集U2和V2,易知U1×U2，V1×V2是X×Y上的非空開集.由f×g是G-混合映射知,?N1∈ N+,?(p1,p2)∈ G,當n>N1時,有

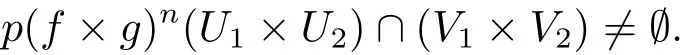
又

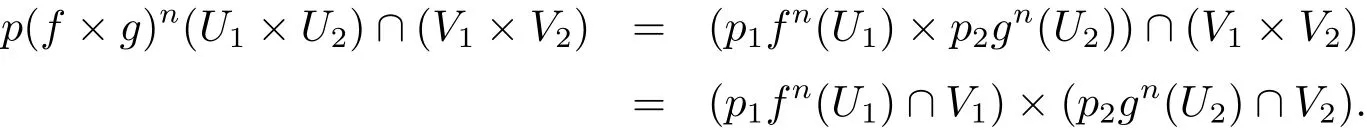
則

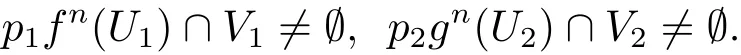
故f是G1-混合映射,g是G2-混合映射.

?假設f是G1-混合映射,g是G2-混合映射.?X×Y上的任意非空開集和易知是X 上的非空開集,是Y上的非空開集.由f是G1-混合映射知,?N2∈ N+，?t1∈G1,當n>N2時,有

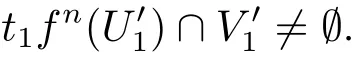
由g是G2-混合映射知,?N3∈N+，?t2∈G2,當n>N3時,有

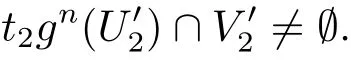
取N4=max{N2,N3},t=(t1,t2)∈G,當n>N4時,有

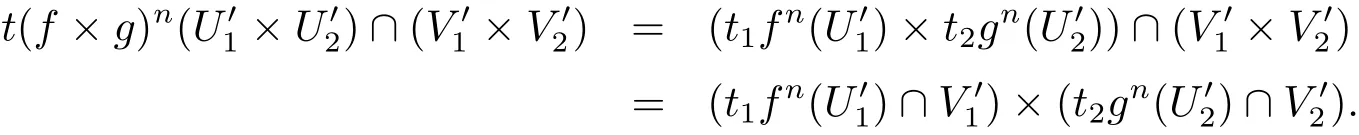
故

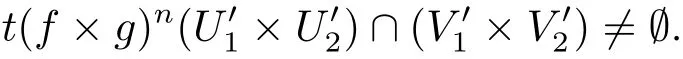
因此f×g是G-混合映射.

定理3.3設(X,d1)是度量G1-空間,(Y,d2)是度量G2-空間,f:X ?→X 連續,g:Y?→Y 連續,則CRG(f×g)=CRG1(f)×CRG2(g).

證 ? 先證CRG(f×g)?CRG1(f)×CRG2(g).設z=(x,y)∈CRG(f×g),?ε>0,則存在f×g作用下的(G,ε)鏈其中zi=(xi,yi),z0=zn=z.故對任意的

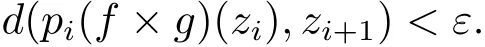
因此

又x0=xn=x,y0=yn=y,則x∈CRG1(f)，y∈CRG2(g),故z∈CRG1(f)×CRG2(g).

?下證CRG1(f)×CRG2(g)?CRG(f×g).設z=(x,y)∈CRG1(f)×CRG2(g),則x∈CRG1(f),y∈CRG2(g).?η>0,則存在f作用下的(G1,η)鏈,其中x0=xm=x,存在g作用下的(G2,η)鏈其中y0=yk=y.取

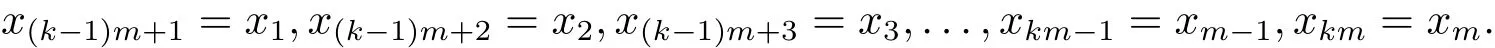
取

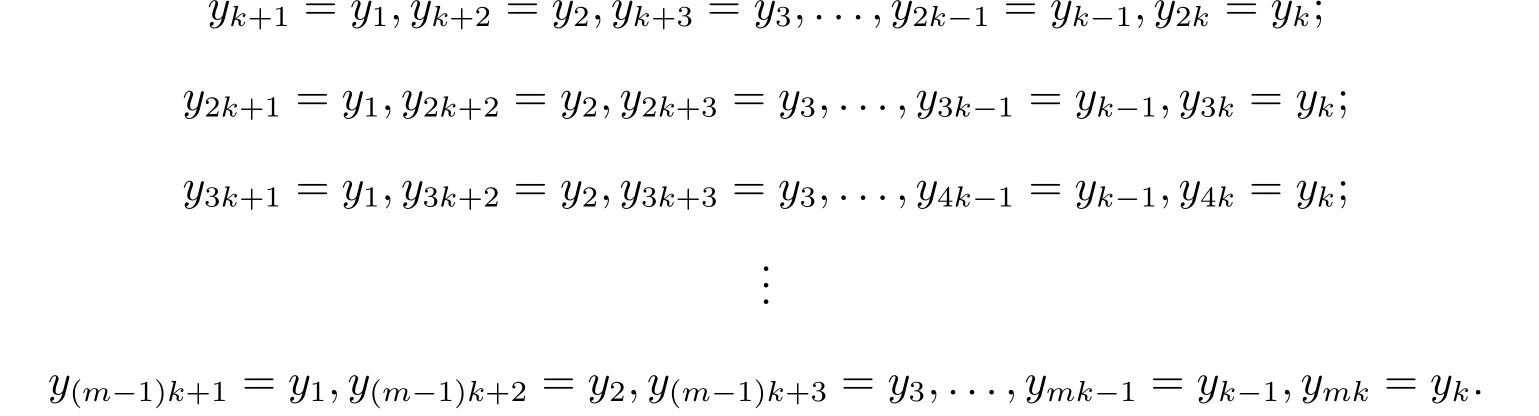
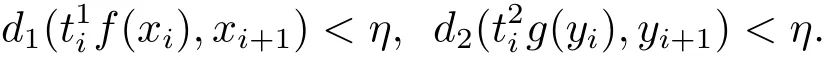
取zi=(xi,yi),ti=則有

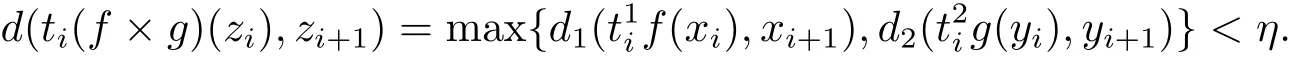
又z0=zmk=z,故z∈CRG(f×g).

4 總結

本文受文獻[8]和文獻[11]研究思路的啟發,在拓撲群作用下的乘積空間中介紹了G-極小映射、G-混合映射和G-鏈回歸點的概念,利用乘積映射的性質,研究了乘積映射f×g與分映射f和g在這些動力學性質方面的關系,得到了較好的結果,推廣和改進了整數加群Z作用下拓撲空間中有關極小映射、混合映射和鏈回歸點的結果,為其在今后實際的應用中提供了理論依據和科學基礎.