例談《橢圓標準方程的推導和化簡》的核心素養培養

☉安徽省臨泉第一中學 李云真

高中數學核心素養的養成方式呈現出多樣化的趨勢，但課堂仍然是主要場所，教師授課仍然是主要方式，因此如何在現有的教學條件下，通過新的技術、新的理念來優化和豐富課堂教學，并實現對學生數學運算核心素養的培養成為了當前高中數學教育的重點和難點.得益于信息化教學工具在高中校園的普及，以信息化教學工具為載體的微課教學憑借著知識點分布全面細致、教師講授便捷明了、學生學習興趣更加濃厚等優點，獲得了越來越多高中數學教師的歡迎.

一、課前學情分析

本文所選用的微課教學設計內容為北師大《高中數學·選修2-1第三章圓錐曲線與方程》第一節“橢圓及其標準方程”的內容.本節微課的教學設計旨在以下三個方面：其一，承上，以“圓”的定義和標準方程推導與化簡為基礎，啟發學生思考，在完成橢圓定義、標準方程推導與化簡的同時，實現對圓的相關內容的復習、應用和強化；其二，啟下，通過對橢圓定義、標準方程推導與化簡的學習進一步強化對圓錐曲線此類問題的分析和解決思路，為后續更多、更為復雜的圓錐曲線問題的分析和解決打下良好基礎；其三，數學運算核心素養，本節微課主要以平面直角坐標系上的橢圓的性質為主，嘗試用三種不同的方法對橢圓的標準方程進行推導和化簡，重點在于培養學生的數學邏輯思維，通過教師的引導與啟發來促使學生自主思考，積極運算，從而切實加強學生的數學運算核心素養的培養.

二、微課設計思路

本節微課教學設計以新課標中關于高中階段數學運算核心素養的具體要求為指導，旨在通過微課設計建立更加豐富的教學方式與更加有效的師生互動，通過講述、啟發、引導、評價和總結等方式充分調動學生自主分析、獨立思考的積極性，加強學生的參與性.基于此，本次微課設計為了實現拓展數學運算思維、培養學生程序化分析的習慣、養成嚴謹求實的數學精神這三大目標，將整個微課教學過程按照6個步驟逐一展開：1.理解運算對象；2.掌握運算方法；3.選擇運算法則；4.明確運算方向；5.設計運算程序；6.獲取運算結果.

三、微課教學實施過程

1.橢圓概念引發

師：同學們有沒有觀察過我們生活中各種各樣的圓形呢？生：圓形的鏡子、地球、雞蛋、車輪、太陽、月亮……師：同學們觀察的很仔細，那么大家能不能對這些不同的圓形進行一下分類呢？

生：鏡子是圓形的，雞蛋是橢圓的，行星的運轉軌跡也是橢圓的……

師：同學們總結的很好，那么我們今天學習的重點就是生活中最常見的幾種圓形中的典型代表之一：橢圓.

師：我知道同學們都能夠熟練地畫出橢圓的大致形狀，那么同學們能不能用我們的數學語言對橢圓下一個定義呢？讓我們先從這個問題入手：

已知存在圓O，點F在圓O內，點P在圓O上，直線l垂直平分PF，同時和PO相交于點M，那么隨著點P在圓O上的位置變化，點M的運動軌跡是什么呢？下面大家一起來看一下.

（教師播放事先準備好的點M運動軌跡的Flash動畫，最終用線將點M的運動軌跡標識出來，出現一個橢圓.如圖1所示.）

師：大家請仔細觀察點M的運動軌跡，然后認真歸納一下直線l

和PO的交點M在伴隨著點P的運動而運動的過程中有什么特征呢？

生：直線l是PF的垂直平分線，那么MP=MF；

師：說得很好！那么大家能不能發現線段MF和線段MO的長度之和有什么特征呢？

圖1

生：MF+MO=MP+MO=OP，所以線段MF和線段MO的長度之和剛好為圓O的半徑.

師：很好.同學們總結的非常正確.從上面的特征分析來看，我們可以得出關于橢圓的概念特征：（1）已知平面內的兩個點（如圖1中的F，O）；（2）橢圓可以理解為到上述兩點的距離之和為定值（如圖1中的圓O半徑）的點的集合.

2.橢圓標準方程推導

師：同學們不妨聯想一下我們學過的關于圓的定義，有哪位同學能夠主動表述一下？

生：平面內到定點的距離為定值的點的軌跡是圓.

師：很好，這位同學的表述很準確.那回過頭再來看橢圓，這里面都包含了“定點”和“定值（2a）”的概念，那么我們不妨以圓的標準方程為參考，找到橢圓方程的表達式.

師：請同學們思考一下，圓中的定值需要滿足大于0的條件，那么橢圓中的定值（2a）呢？

生：大于0！

師：沒錯，但是同學們能不能把這個范圍再做進一步的縮小呢？大家看點M隨點P運動的軌跡，當2a=FO時，會出現什么情況呢？

生：F、M、O三點共線，無法構成橢圓，所以2a還要大于FO！

師：很好.綜合上述同學們的思考，我們得出以下結論（為了便于表述，我們可以將圖1中的點F改為F1，點O

（1）橢圓屬于平面范疇內的幾何圖形；

（2）點F1、F2通常被稱為橢圓的焦點，同時要滿足2a＞F1F2＞0；

師：請同學們參照上述的分析過程，認真的默讀幾遍橢圓的定義，

師：很好.那么請同學們思考一下應該如何獲得橢圓方程的表達式呢？請參照圖2.

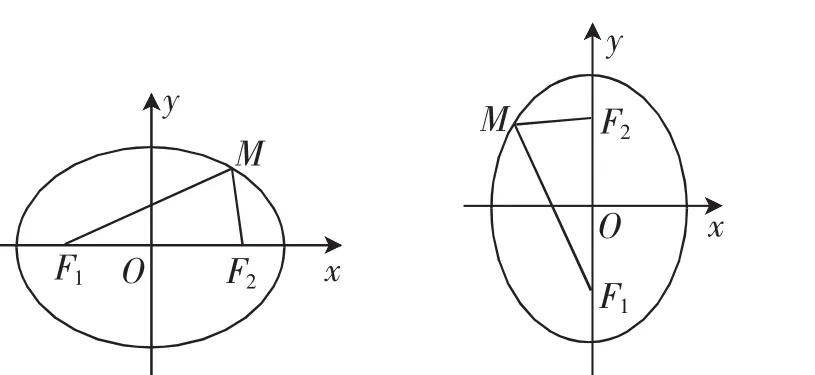
圖2 橢圓標準方程的推導

生：根據橢圓的對稱性！

師：很好，那么有沒有哪位同學想要來推導一下呢？

師：同學們可按照下述假定條件進行推導.（如圖3所示）

設橢圓O上的點M（x，y），由MF1+MF2=2a，得

其中兩名同學的實際推導過程（板書）如下表1所示：

表1 橢圓標準方程的推導和化簡學生推導板書

3.橢圓標準方程化簡

師：好，兩位同學的化簡過程都是一種可以采取的思路，但是我們來看生2同學化簡到最后發現項數變得越來越多了，很難繼續化簡下去了，那么有沒有其他同學想要嘗試化簡一下呢？

師：好，大家請注意老師的化簡過程.c

師：請同學們看一下上式的形式，等號左邊符合（m+n）（m-n）的形式，等號右邊則是（m-n）2的形式，所以繼續化簡如下：

也即：（a2-c2）x2+a2y2=a2（a2-c2）………（2）

化簡到這一步，是不是和生1同學的結果完全相同了.

生：沒錯，是的.

師：很好，為了進一步簡化橢圓方程，我們可以令a2-c2=b2（a＞b＞0），

師：通過今天的學習，我們主要掌握了橢圓標準方程以及推導化簡的方法.要完成一個推導化簡的過程，可采用的方法并不是單一的，不同方法在運算的難易程度上也有著較大的區別，所以老師想請同學們在后續的復習中思考如下幾個問題：

1.本節課所學習的兩種化簡方法哪個簡單，哪個復雜，為什么復雜？

2.通過橢圓標準方程我們能夠得出橢圓的哪些幾何性質？

3.在你發現的這些橢圓的幾何性質中，有哪些是可以通過表達式表述出來的？

在下節課的學習中，讓我們一起來回答上面幾個問題.

結語：數學是注重思維邏輯的學科，用符合不同年齡段的學生學習規律的學習方法才能更好地達成教學目標.課標中對高中段學生數學核心素養的界定，幫助教師明確了教學的基本要求，有助于教師在課堂——這一教學主要場所中更好地發揮教學的能動性；其次，有效提問是連接不同教學內容來啟發學生主動思考的有力工具.在上述微課的教學設計中，即采用了大量的啟發性提問，不斷地引導學生自主思考，一方面提高了學生的參與性，同時也有助于幫助學生加深認知，并逐步養成針對運算問題自主總結、積極歸納運算方法的好習慣.綜合來看，在本次的微課教學設計中，教師的主導性仍然過高，在很多結論的得出方式上仍然以教師總結為主，在后續的教學過程中可以進一步激發學生的自主性，讓學生一步步的自主探索、總結、歸納，通過讓學生全程參與到思考和問題分析的過程中，來幫助學生獲得更為明晰的學習成就感，并在此過程中更好地塑造和培養學生的數學運算核心素養.W