積極引導探究，讓數學教學更有效

☉江蘇省揚州市邗江區瓜洲中學 沈 亮

從某個角度來說，數學教學就是教會學生如何學數學.教師講學生聽的這種教學模式雖然由來已久，但已經不能適應當前的教學形勢.讓學生變被動學習為主動學習，把學習的權利交還給學生，讓學生主動探究，已經成為數學教學模式的主流.那么，教師應如何積極引導學生探究，讓數學教學變得更有效呢？在此，筆者談談在數學課堂教學中滲透探究性學習的一些體會，供同行參考.

一、在新授課的概念教學中引導探究性學習

數學學習一般是從概念與定義開始.在這些概念與定義的教學中，由數學概念與定義的產生，該如何得到概念與定義？又該如何理解這個概念與定義呢？這些都由教師一人承擔，而學生只是默默地聽，默默地記，長此以往的后果就是學生的思維能力不斷下降，甚至萎縮，學生學習的積極性蕩然無存.

如，在《雙曲線》教學中，部分教師這樣展開教學：

我們已經知道，與兩定點的距離的和為常數的點的軌跡通常是橢圓，那么與兩定點的距離的差為非零常數的點的軌跡是怎樣的曲線呢？我們一起做個實驗！（教師在黑板上演示）

工具：圖釘，筆，拉鏈.

方法：將拉鏈拉開一部分，在拉開的兩邊上各選取一點，分別固定在F1，F2上，點F1到點F2的長為2c（c＞0）.把筆尖放在M處，隨著拉鏈逐漸拉開或閉攏，筆尖就畫出一條曲線.

請大家想一想：這條曲線是滿足什么條件的點的集合？（引出下面問題）

平面上與兩定點的距離的差的絕對值為非零常數的動點的軌跡是什么？

教師講解：設這兩個定點分別為F1與F2，動點為P，非零常數為2a，則有||PF1|-|PF2||=2a，

（1）在0＜2a＜|F1F2|條件下：|PF1|-|PF2|=2a時為雙曲線的一支（含F2的一支）；|PF2|-|PF1|=2a時為雙曲線的另一支（含F1的一支）.

（2）當2a=|F1F2|時，||PF1|-|PF2||=2a表示兩條射線.

（3）當2a＞|F1F2|時，||PF1|-|PF2||=2a不表示任何圖形.

教師引導：在雙曲線的定義中應當注意2a=||MF1|-|MF2||＜|F1F2|=2c這一條件.例如：平面內一點M到兩定點F1（-4，0），F2（4，0）的距離差是6時，點M的軌跡是雙曲線的右支，當差等于8時，點M的軌跡是兩條射線，當差大于8時無軌跡，這幾種情形都不是雙曲線.理解雙曲線應注意理解定義中的條件.

上述教法，從數學知識的角度來看，無可挑剔，而從引導學生學習的角度來看，有待商榷.因為在這個教學過程中，教師充其量就是一個表演者和解說員，學生都成了看客，不能夠主動加入到探究雙曲線概念的活動中來.那么如何讓學生主動參與到探究活動中去呢？教師必須要創設探究情境.

例如在《雙曲線》這節概念課中，教師應該讓學生主動動手實驗，通過畫雙曲線的實驗活動，讓學生自己總結雙曲線的定義，并思考|PF1|，|PF2|與|F1F2|的數量關系.這樣把問題拋向學生，學生自然會通過主動探究，來獲知利用雙曲線定義時的幾個注意點.

筆者以為，要想讓學生學會探究，教師應該從概念教學開始，積極創設探究情境，并積極引導學生主動探究.

二、在習題教學中引導學生探究性學習

習題教學既是數學教學的重要組成部分，也是引導學生探究性學習的主要環節之一.在教學過程中，教師可以從不同角度引導學生進行思考，從而誘發新問題，發展新思維，進而把學生引向探究境地.因此可以是對問題的變式進行探究，以問題串的形式出現，由淺入深，由簡單到復雜，環環相扣，步步為營，讓學生探究起來欲罷不能，也可以是一題多解式探究，讓學生通過對多種解法的探究，感悟數學知識的內在聯系，欣賞數學世界的無限風光.尤其是在高三復習課上，要讓學生通過一題多解的方式來展現自我的探究能力.

如，在平面向量一輪復習中，筆者讓學生以下面一題為載體，探究多種解法.

例題給定兩個長度為1的平面向量，它們的夾角為120°.如圖1所示，點C在以點O為圓心的圓弧

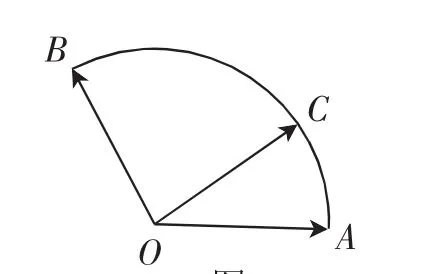
圖1

經過學生集思廣益，從多角度進行探究，竟然發現了7種解法，令人贊嘆.

學生分別從特殊值法，坐標法，函數法，不等式法，利用數量積轉化為方程問題等多個角度加以探究，最終獲得7種解法.限于篇幅，本文選摘其中的兩種思路來求解，以饗大家.

1.考慮向量的數量積的運算

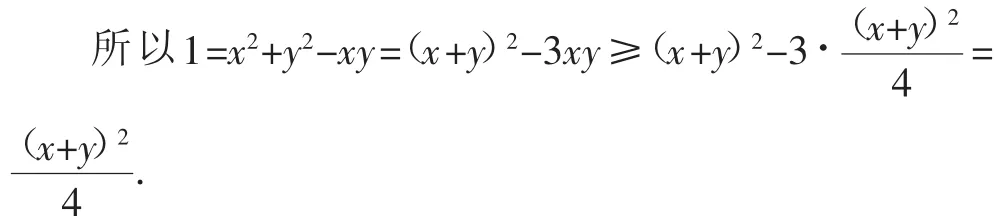
所以x+y=2［cosα+cos（120°-α)］=2sin（α+30°）.

所以當α=60°時，（x+y）max=2.

解法2：（兩邊平方法）因為

所以x+y≤2，當且僅當x=y=1時取等號.

所以（x+y）max=2.

2.考慮平行四邊形法則

解法3：過點C作CM∥OB交OA的延長線于點M，作CN∥OA交OB于點N，則四邊形OMCN是平行四邊形.由向量加法的平行四邊形法則得：△OMC中，設∠AOC=α，則∠BOC=120°-α，且|OM|=x，|MC|=y.

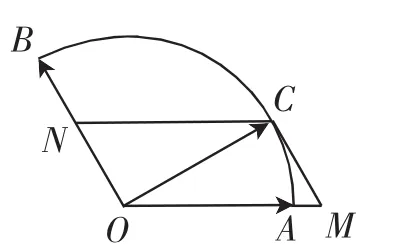
圖2

由正弦定理可得：

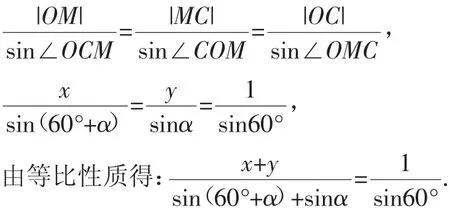
所以x+y=2sin（α+30°）.

所以當α=60°時，（x+y）max=2.

解法4：由余弦定理可得|MC|2-2|OM|·|MC|cos60°，

即1=x2+y2-xy=（x+y）2-3xy≥（x+y）2-3·

所以x+y≤2，當且僅當x=y=1時取等號.

所以（x+y）max=2.

從以上學生的探究過程中不難發現，只要教師因勢利導，學生的數學能力必將得到極致的發揮.常言道：群眾的力量是無窮的，讓學生合作學習，通過探究，往往能起到1+1＞2的效果，也更能體現出探究性學習的價值.

三、在開放式問題的解決中引導探究性學習

數學問題具有嚴謹性的特點，雖然可以訓練學生思維的嚴謹性，但數學問題更需要具有開放性的特點，因為開放式問題更能引導學生積極探究，主動創新.因此，在數學教學過程中，設計開放式問題，甚至答案不唯一，不確定的數學課題，是學生開展探究性學習的最有效的載體.在平時的教學中，可以讓學生總結解題規律，總結某知識點的用途，甚至可以讓學生研究歷年高考題的題型分布，讓學生從學習的初級階段向高層次的探究階段轉化.

比如，在學習了函數單調性之后，筆者給學生布置了這樣一道開放題：

函數單調性有哪些用途，試舉例說明.

這是一個開放式探究性問題，學生經過合作探究，得到了如下成果（例題解答略）：

1.利用函數單調性解方程，如：解方程2x3+x=18；

5.利用函數單調性證明不等式，如：已知a，b，c∈R+，c＜a+b且c＞a-b，求證：

在數學教學過程中，創設數學開放式問題，既是培養學生探究能力的需要，也是培養學生數學核心素養的體現.

總之，選擇適當的教學方法進行數學教學，引導學生進行探究性學習，是培養學生綜合能力的重要環節，是教學改革的必然趨勢，是培養學生數學核心素養的關鍵.