雙頻InSAR高程重建噪斑去除方法
藺祥楠, 禹衛東
(1.中國科學院電子學研究所, 北京 100190; 2.中國科學院大學, 北京 100049)
0 引言
干涉合成孔徑雷達(Interferometric Synthetic Aperture Radar, InSAR)是通過計算兩幅配準后的SAR復圖像的干涉相位差,結合地表高度和干涉相位差之間的關系,獲取地表三維信息的重要遙感技術[1]。傳統單頻率相位解纏前提是相鄰像素的絕對相位差小于π。實際就是要求待解纏的區域比較平緩,沒有陡變地形。此外,單頻率相位解纏算法計算方法復雜,且噪聲敏感性高,誤差傳遞現象嚴重。因而傳統單頻干涉SAR無法有效解決某些復雜地區的高程重建問題。為了實現復雜地形的DEM(Digital Elevation Model)反演,提出了多通道InSAR測量技術。
多通道InSAR測量技術[2]包括多頻率InSAR測量技術[3]和多基線InSAR測量技術[4]。多頻率InSAR通常選取互質的載頻波段來增大高度模糊數。多基線InSAR技術則是利用不同的基線來增大高度模糊數。模糊高度數的擴大,有利于得到更為精確的解纏相位信息。
多通道干涉SAR技術發展迅速,高度重建算法種類眾多。其中較為早期的一種方法是多通道最大似然估計(Maximum Likelihood Estimation, MLE)算法[5]。該算法利用干涉相位的概率統計特性直接進行高程重建,重建速度快,但受干涉通道數目、基線長度、工作頻率、相干系數的影響特別大,抗噪能力弱,在相干系數低的區域需要增加很多的通道數來保證精確度[6-7]。為了解決MLE中過高的通道數要求和重建精度的矛盾,基于Markov隨機模型的MRF-MAP(Markov Random Field Based Maximum a Posteriori Estimation)算法被提出來。該方法利用Markov模型作為先驗分布,通過估計每個像素的超參數實現高程重建。至今,有許多人提出了改進的MAP算法[8-9]。雖然MRF-MAP提高了反演精度,但該方法需估算每一點的超參數,運算時間過長,設備要求過高[10]。相比之下,ML算法在計算速度上擁有絕對的優勢,適合做大數據量的數據處理。但ML估計結果噪聲點和噪聲聚集成斑塊的現象嚴重,本文提出了ML估計結果噪聲斑塊去除方法。具體方法是:首先利用聚類分析[11](CA)思想去掉解纏結果中大量出錯區域對應的模糊類;再利用變長滑動加權窗口判定并去除噪斑,得到正確的解纏相位。
1 基于MLE的雙頻干涉高程重建方法
雙頻系統可以通過兩個互質的頻率增大高度模糊數,從而實現更復雜地形的高程反演。在基于MLE的高程重建算法中,高程重建問題被轉化成了找到高程值h(p)使似然函數達到最大化的問題。
在單通道InSAR中,對于圖像的每個像素點(i,j),纏繞的干涉相位φ′與地表高程信息之間的關系為
(1)
式中,λ為載頻波長,〈·〉2π為“模2π”處理操作,μ為一個比例系數,由InSAR系統收發模式以及飛行參數確定:
(2)
式中,B⊥為垂直斜距平面的基線分量,r0為該點斜距,θ為該點斜視角。
根據InSAR干涉相位的統計特性,得到干涉相位的概率密度統計特性:
f(φ|φ′)=
(3)
將式(1)代入式(3)可以得到測量干涉相位與高程信息之間的概率密度分布函數:
f(φ|h)=
(4)
式中,γ稱作干涉圖像的相關系數:
(5)

(6)
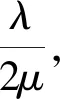
(7)
為了解決無數個最大似然解的問題,增加獨立的觀測相位,采用雙頻干涉技術,式(4)中的各個變量加上角標則得到了各個通道對應的似然函數。此時,總的似然函數變成

(8)
利用聯合最大似然估計方法進行高程重建,多頻率最大似然估計高程值如下:
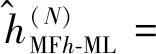
(9)
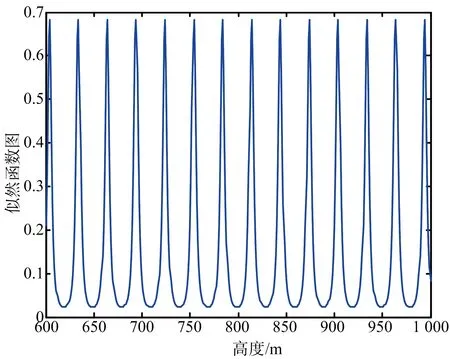
(a) 通道1似然函數
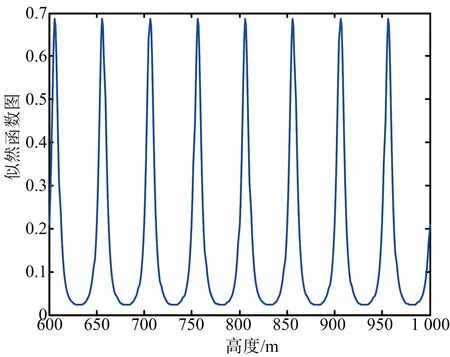
(b) 通道2似然函數
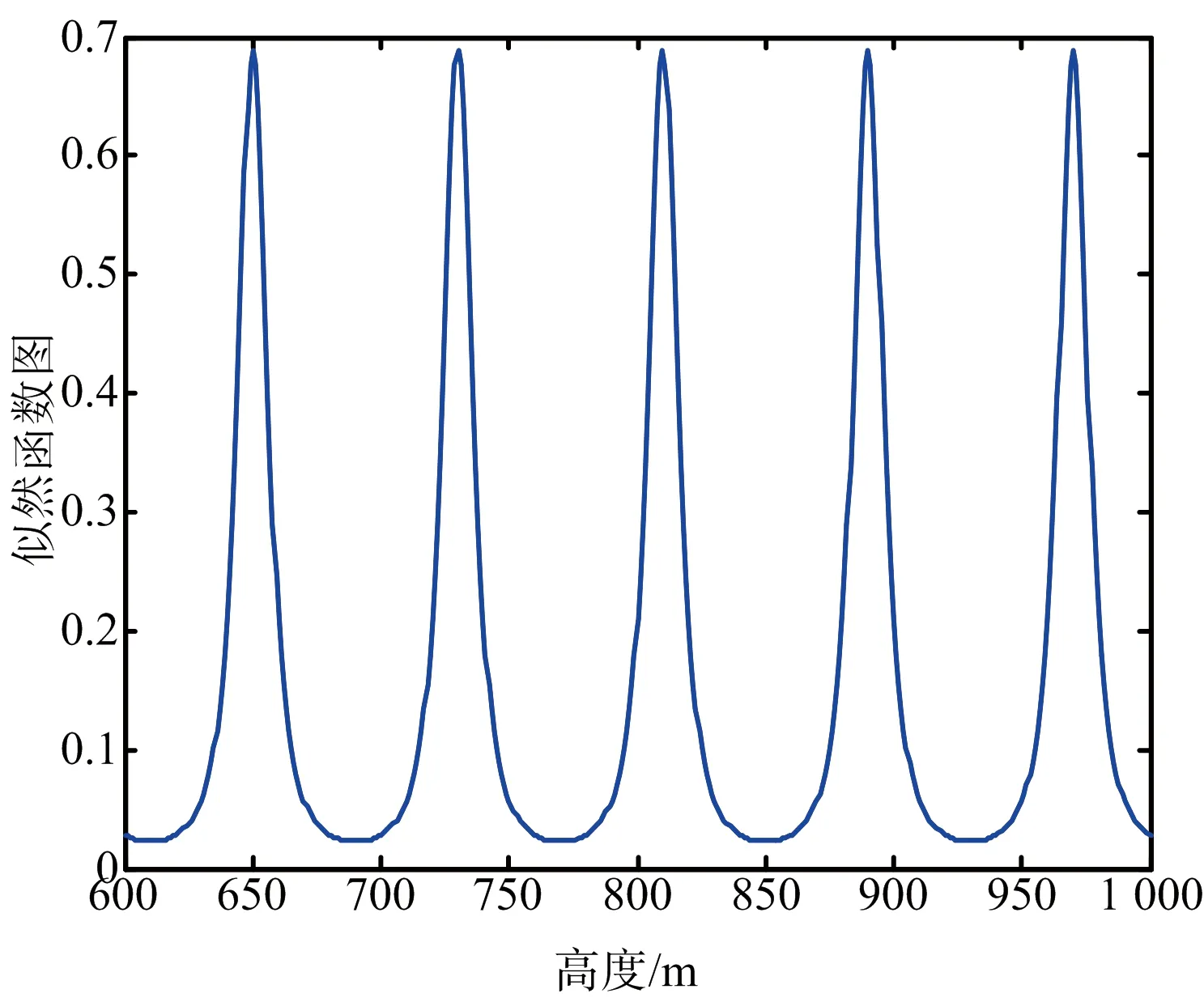
(c) 通道3似然函數
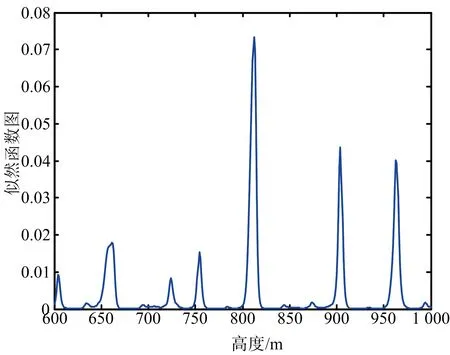
(d) 多頻干涉系統似然函數圖1 單頻似然函數和多頻似然函數示意圖
2 MLE重建結果噪斑去除方法
MLE的雙頻高程重建算法魯棒性不強,得到的結果中有單點噪聲和噪聲斑。由文獻[6]可知,這些噪點高程都與周圍點的高程相差很大。此外,若高程范圍選擇得當,MLE重建結果中噪聲像素所占比例較小。基于這兩點,本文提出了一種噪聲斑塊去除方法。能在保證處理效率的同時,能夠提高重建精度。具體去噪方法分為兩個部分。
2.1 變鄰域錯點標記
根據文獻[11],將像素的模糊矢量定義為該像素在各個干涉通道下的模糊數所組成的矢量。各個干涉通道下p像素的模糊數為
(10)
式中,?·」表示下取整運算。這樣,p像素所對應的模糊矢量即為
V(p)=[n1(p),n2(p),…,nk(p)]
(11)
根據聚類分析的思想,將高程值按高度模糊數進行聚類分組。通過執行以下幾個步驟來進行錯點標記:
1) 構建初始標記矩陣,大小與圖像大小相同,初始值均為1。
2) 根據目標地段高度范圍粗略計算出高度模糊區間,區間之外的點判定為錯點,標識符標記為0。標記出明顯出錯的解纏壞斑。
3) 若某一個模糊類所對應的像素個數低于預期比例閾值,判定為噪聲并將該分組內的像素標識符標記為0。
4) 通過目標點高程與3×3鄰域內重建正確點的高程均值的歸一化差值來判斷該點是否為噪聲點。將噪點像素的標記置為0。
當相鄰的一片像素點均為壞點時,3鄰域均值判定噪點的方法不再起作用。鑒于噪聲斑的大小不一,采用可變鄰域的判別器來判定突變噪聲斑,從而達到將連城小片的噪聲斑進行標記的目的。
2.2 非均勻加權濾波
前面的步驟已經將誤差較大的錯點標記出來。傳統均值濾波會將錯點帶入到加權中使得高程誤差變大。此外,MLE解纏結果中解纏錯誤的部分區域也含有變化的高程信息,解纏出錯的區域只是表現為該區域的整體抬高或者降低,不能將錯點的像素權值全部設為0,因而采用比例加權的方式計算錯點的加權系數。
假設U(p,k)是以p為中心,可調控值k作為寬度的方形鄰域。p′是在U(p,k)內除了p點之外的鄰域像素。
解纏正確的點的均值為
(12)
解纏錯誤的點的均值為
(13)
從而計算出錯點的歸一化加權系數為
(14)
得到錯點修正DEM為
(15)
1)wp′為領域內各點的第一個加權系數。在U(p,k)內,若被標記為解纏錯點,則其值為0,若被標記為正確的點,其值為1。
2)γN(p′)為鄰域各點的第二個加權系數,將其權值設定為U(p,k)鄰域內解纏正確的像素的高程均值和解纏出錯像素的高程均值之比。
綜合以上兩個部分,通過選取合適的模糊類閾值,調節合適的標記窗口和非均勻加權濾波窗口來去除噪聲。窗口選擇時可以利用小窗口方法去掉斑點噪聲,利用大窗口去除噪聲斑塊。而且由于本文方法不是將帶有高程信息的噪斑完全丟掉,如此便可以在保證解纏效率的同時提高重建精度。
3 實驗結果與分析
實驗分為兩個部分,分別是建模驗證(3.1節)和實測數據驗證(3.2節)。建立的仿真模型為一個城市地形和一個帶有懸崖的真實DEM模型,適合驗證雙頻重建算法。仿真模型中的干涉圖均為根據舍選法[12]生成的干涉圖。實測數據為機載C/X雙頻干涉SAR數據,比較適合驗證雙頻干涉算法。實驗主機平臺內存為8 GB,CPU主頻為 3.2 GHz。仿真代碼為Matlab代碼。
3.1 仿真數據處理
仿真數據的參數如表1所示。本節均采用該參數進行仿真。第一個模型最大高程差為250 m,兩個通道的相鄰像素的相位差分別可達到34.79π和19.58π,適合用雙頻干涉算法進行處理。第二個模型為美國Isolation Peak的真實地形仿真模型。峭壁的高度差可達137 m。對應的兩個通道相鄰像素的相位差可達19.07π和10.73π。對模擬數據的處理結果用誤差圖和歸一化均方誤差σ2來進行分析。σ2由如下公式給出:
(16)
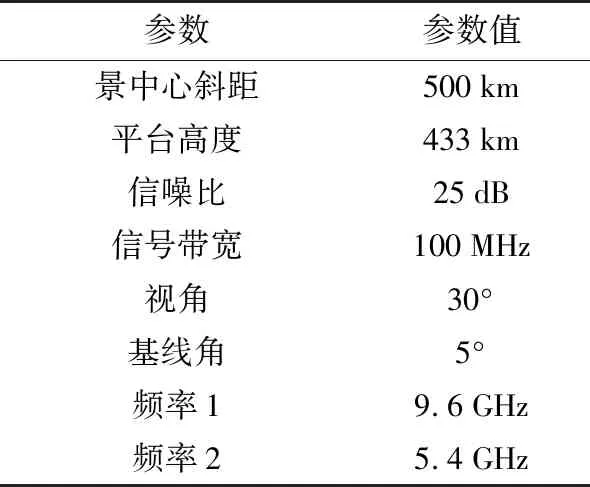
表1 仿真模型主要參數
3.1.1 仿真城市地形
建立的仿真地形DEM投影圖如圖2(a)所示。其中三棱柱形高度為250 m。舍選法所得的兩個通道的干涉圖形如圖2(b)、圖2(c)所示。
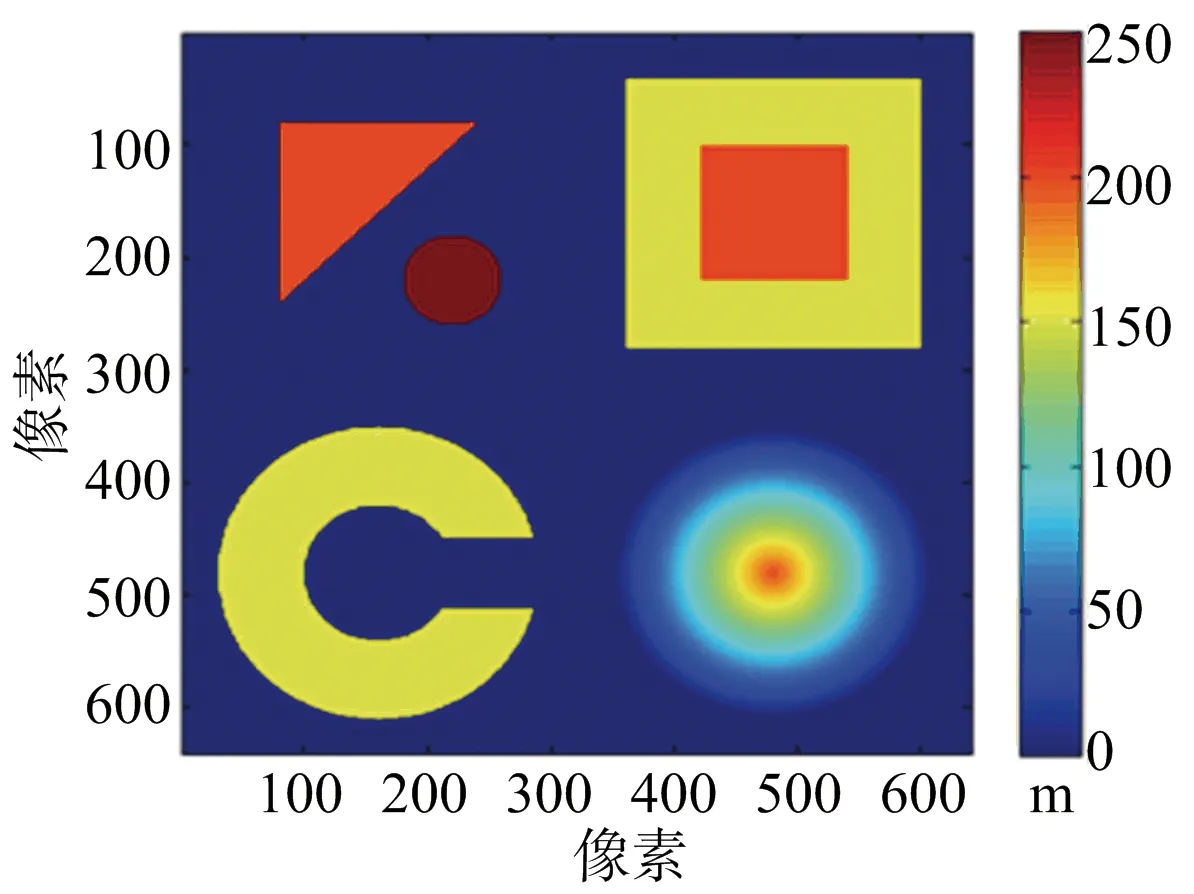
(a) 仿真地形投影圖
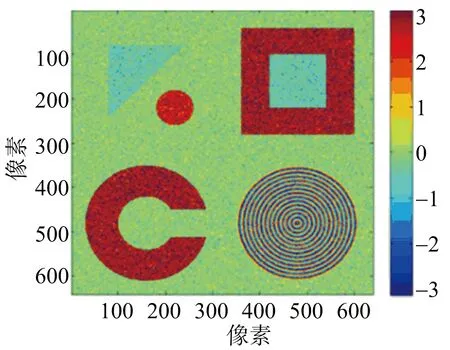
(b) f=9.6 GHz干涉圖
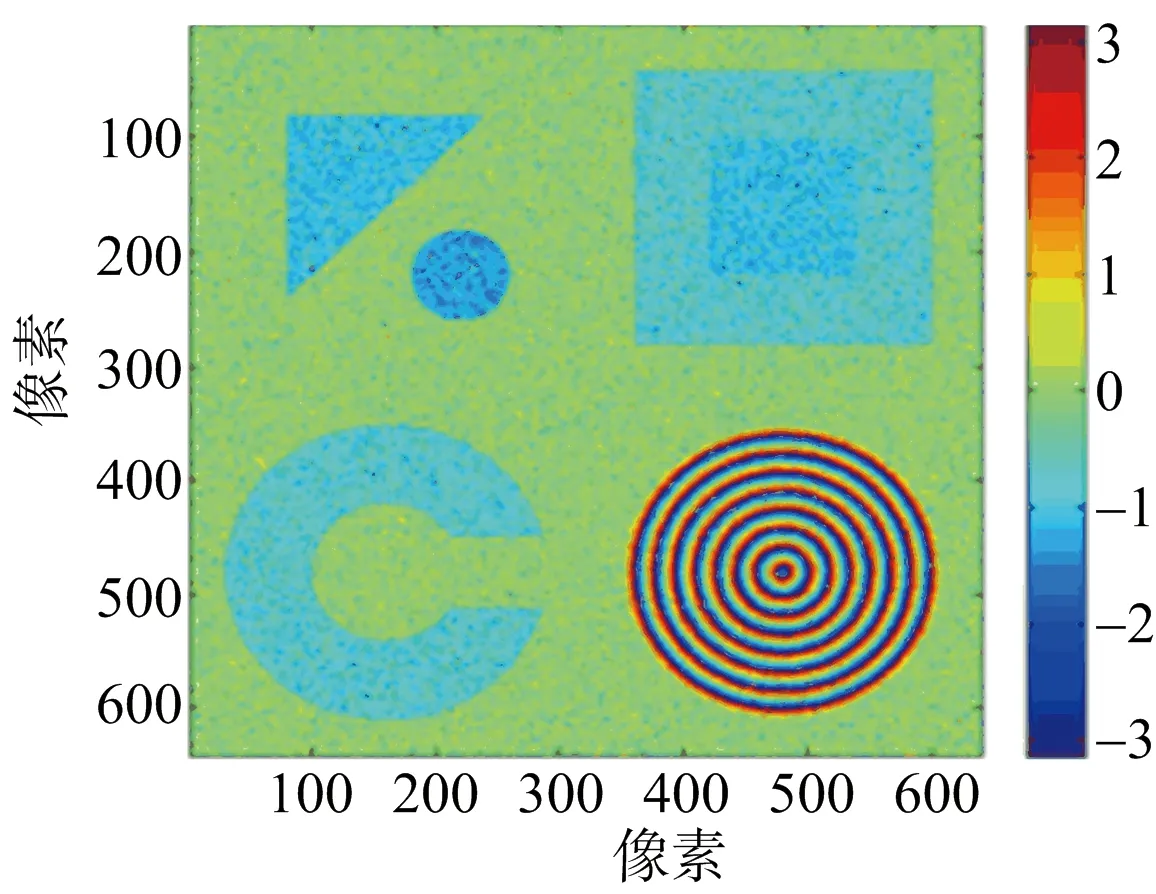
(c) f=5.4 GHz干涉圖圖2 仿真城市地形數據
反演所得MLE結果如圖3(a)所示,可知MLE結果中含有大量的噪斑。利用本文算法去噪點所得到的結果如圖3(b)所示,二次去噪斑結果如圖3(c)所示。從結果看出,重建的高程基本將MLE結果中的噪斑去掉。
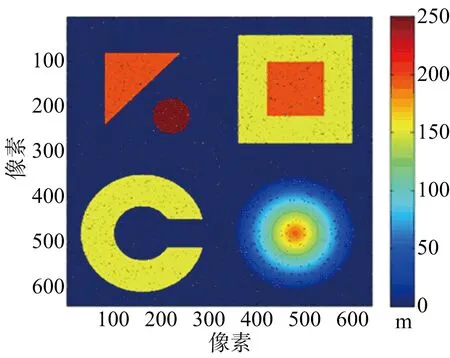
(a) MLE重建結果
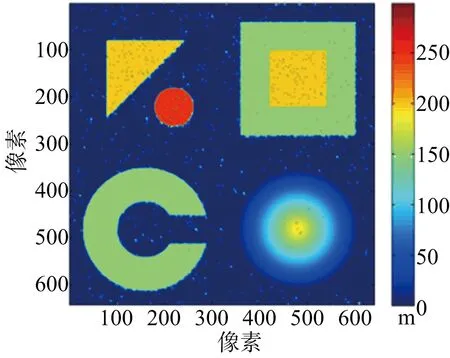
(b) 噪點去除結果
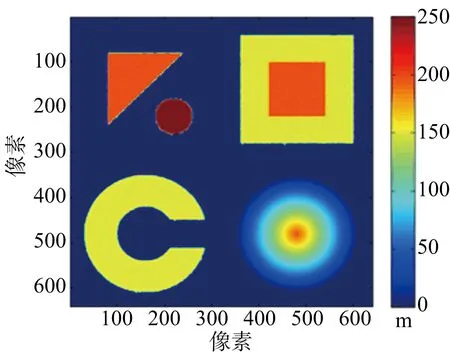
(c) 噪斑去除結果圖3 仿真城市地形去噪斑
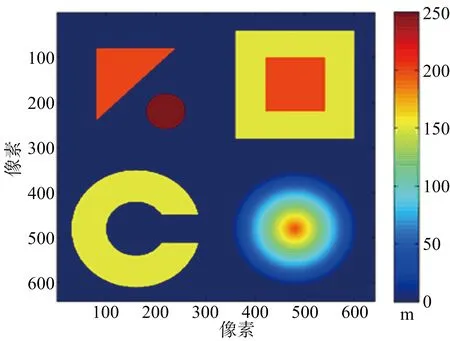
(a) 原始DEM投影
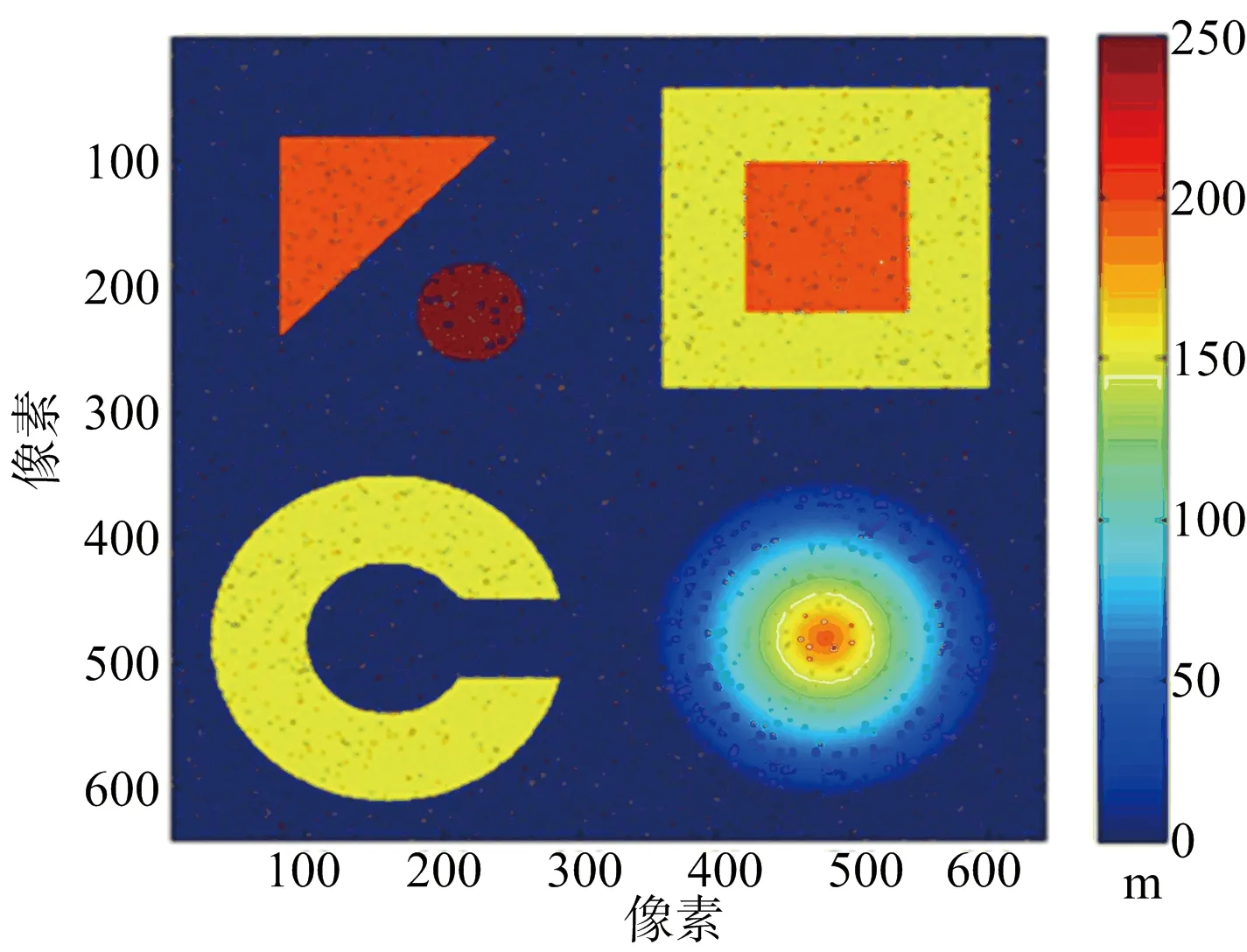
(b) MLE重建DEM投影
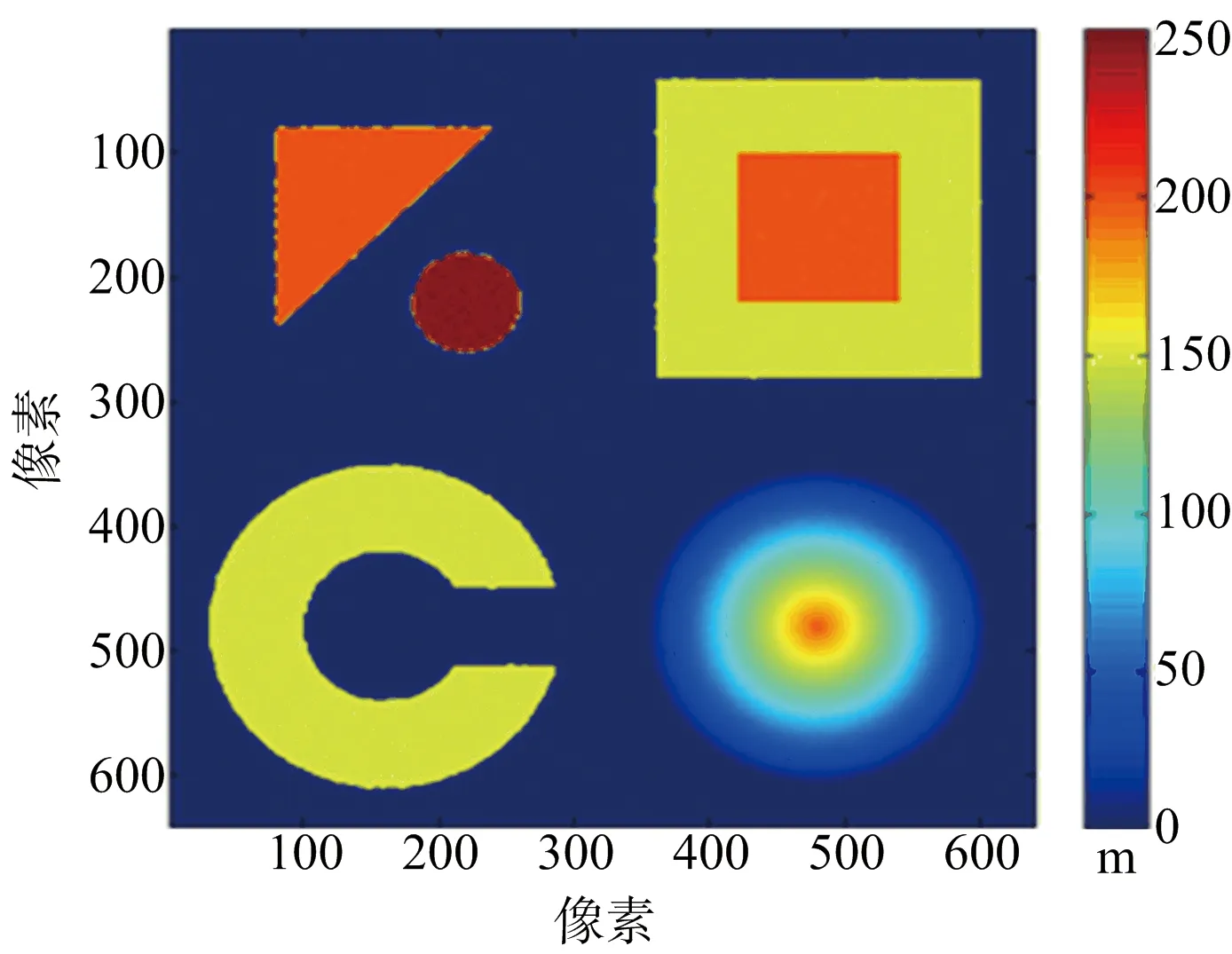
(c) MAP重建DEM投影
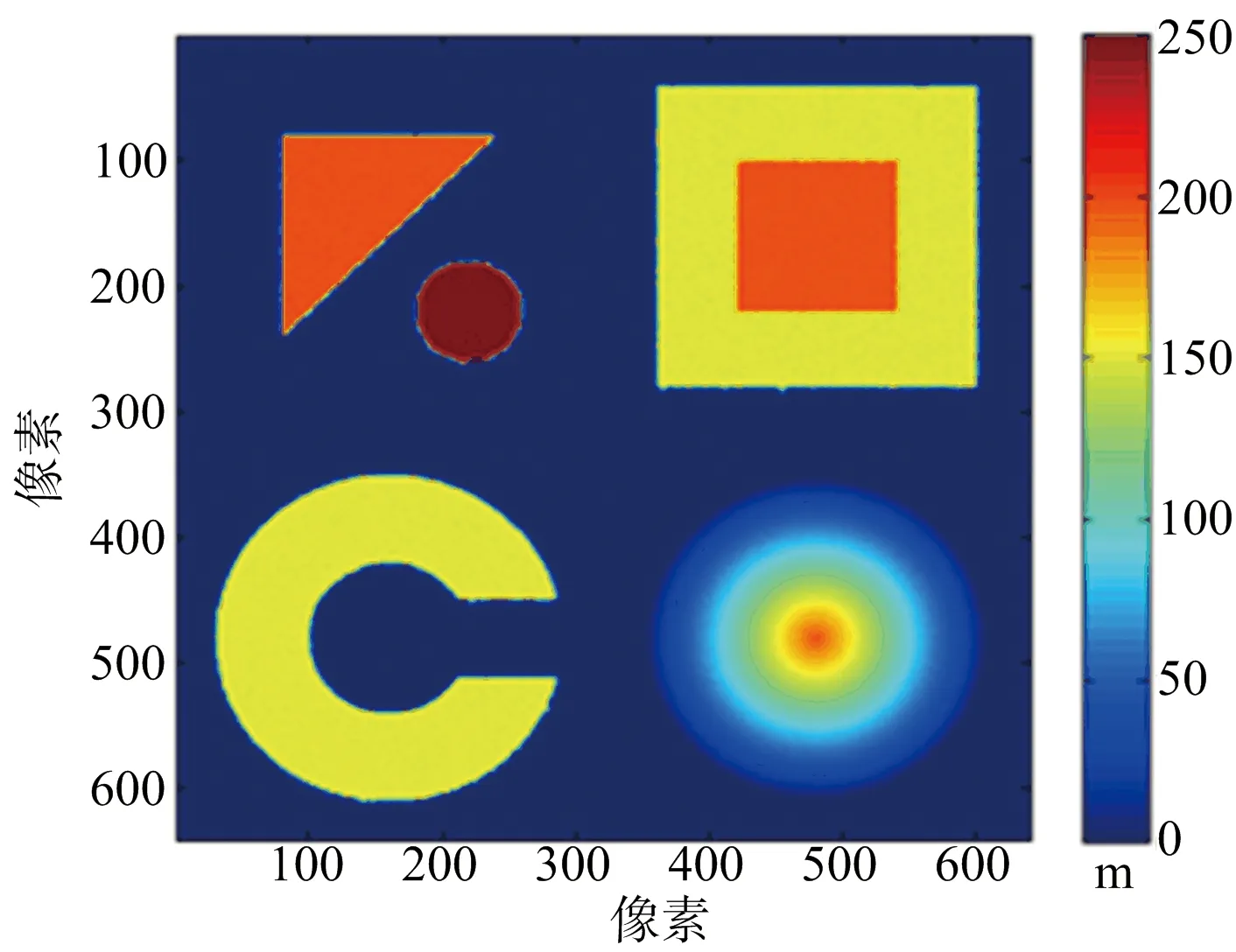
(d) 本文重建DEM投影圖4 仿真城市地形各種重建算法DEM與原始DEM對比
圖4分別列出原始DEM、MLE算法DEM、MAP估計DEM、本文算法DEM來進行對比。3種重建算法的誤差圖分別如圖5(a)、圖5(b)、圖 5(c)所示。統計的各種重建方法歸一化均方誤差如表2所示。重建耗時上:MLE約13.53 s,本文方法約15.61 s;MAP估計達到1 493.14 s,是本文算法的將近100倍。從歸一化誤差來看,MLE算法最差,本文方法和MAP估計相近。
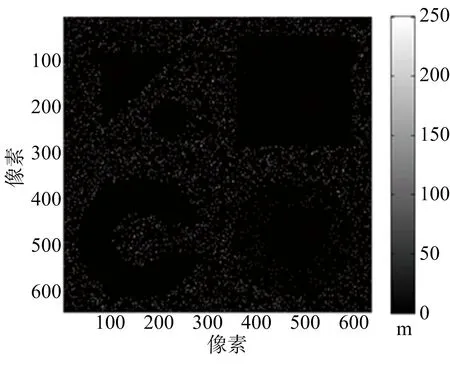
(a) MLE重建誤差圖
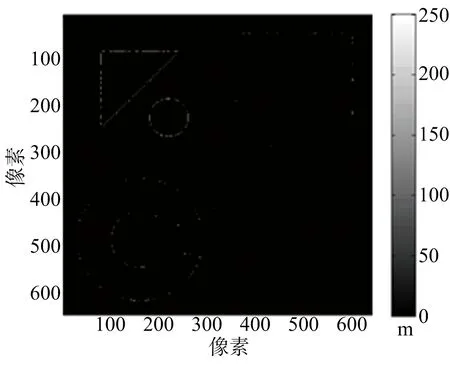
(b) MAP重建誤差圖
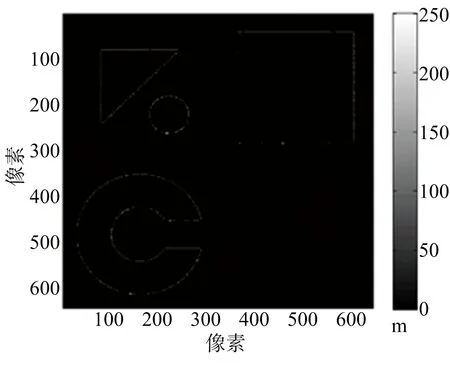
(c) 本文方法重建誤差圖圖5 仿真城市地形各種重建算法誤差圖

重建方法歸一化均方誤差MLE0.3268MAP0.0056本文方法0.0064
圖6給出各種算法重建結果與原始DEM三維對比。該圖證明本算法在精度上表現較為優異。
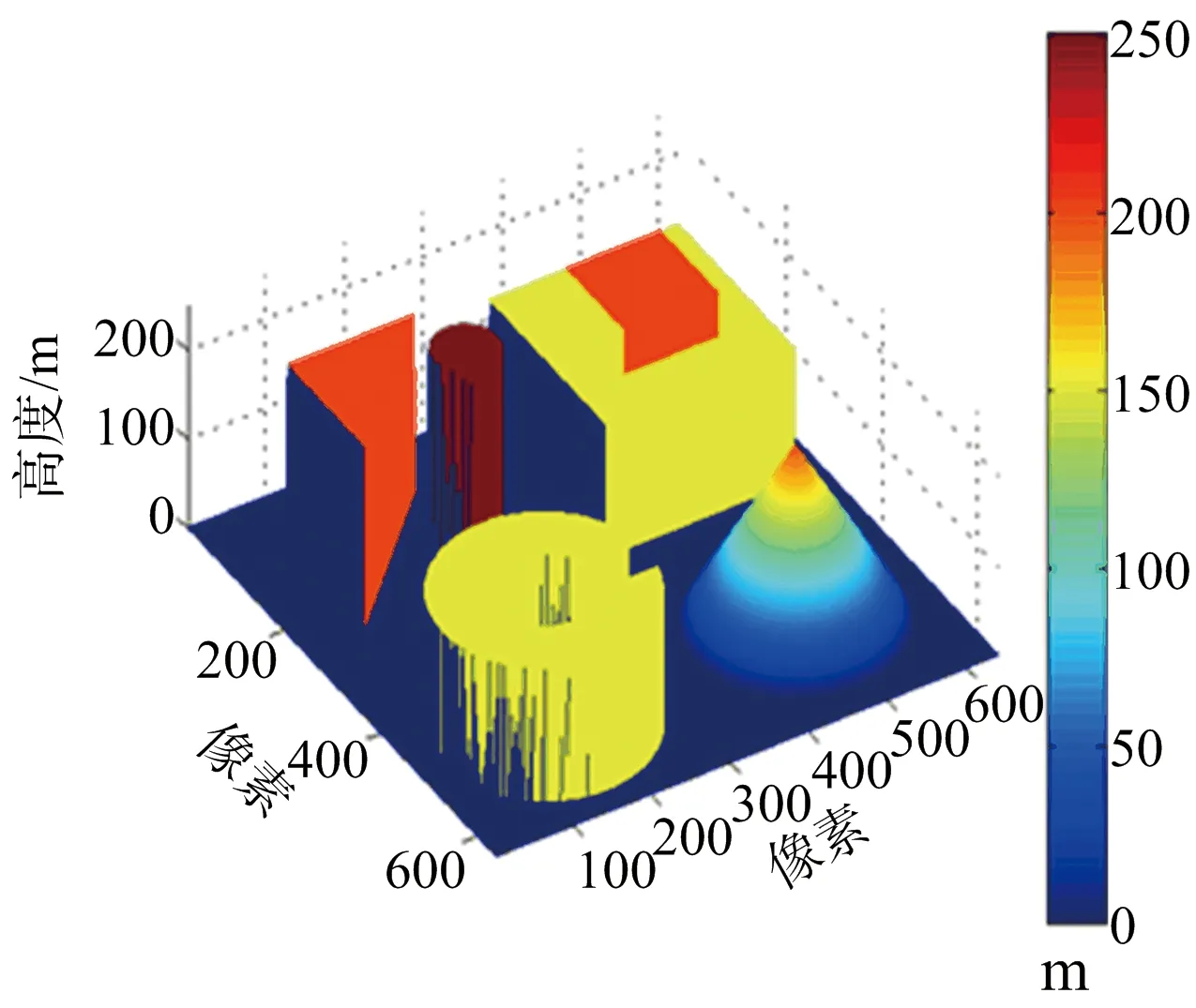
(a) 原始DEM

(b) MLE重建DEM
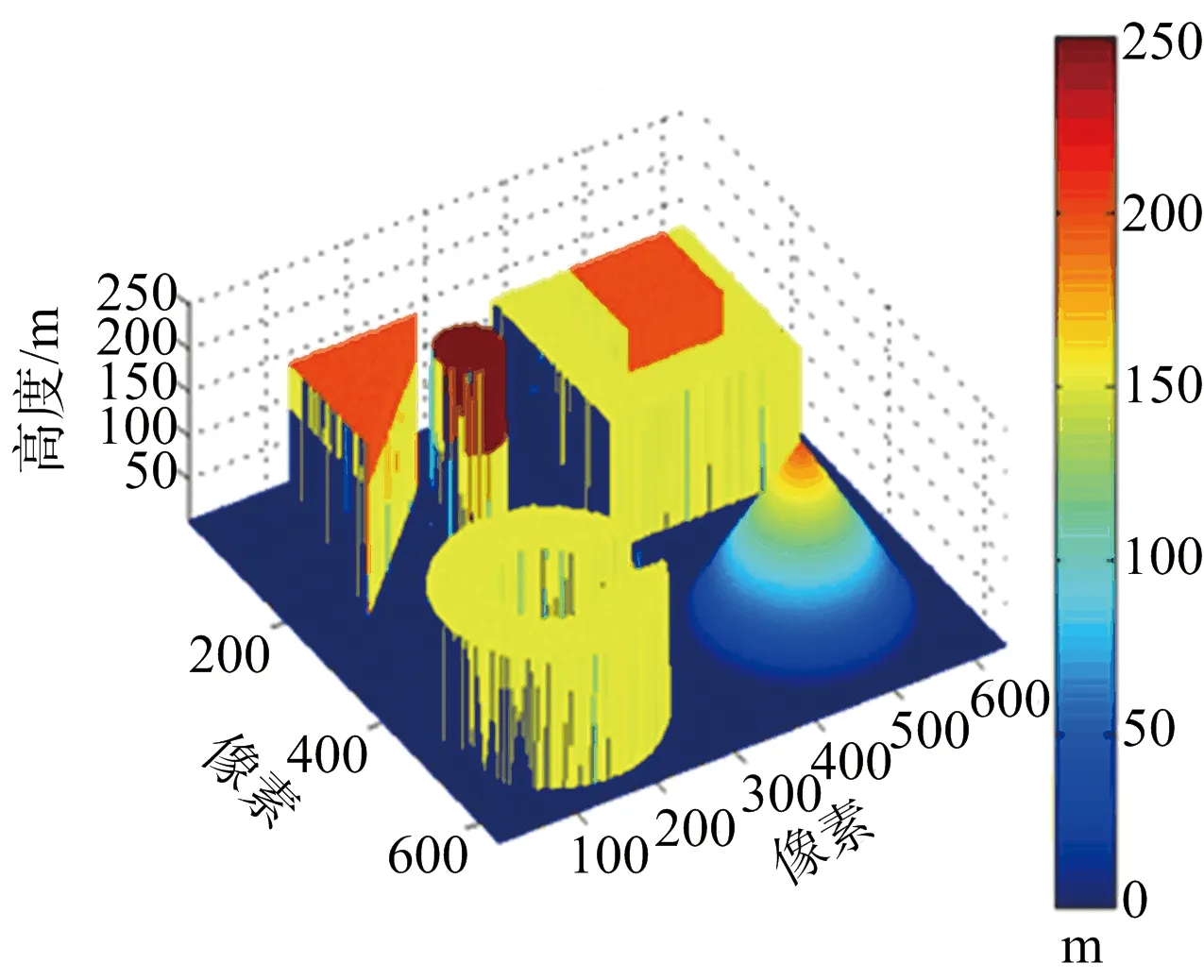
(c) MAP重建DEM
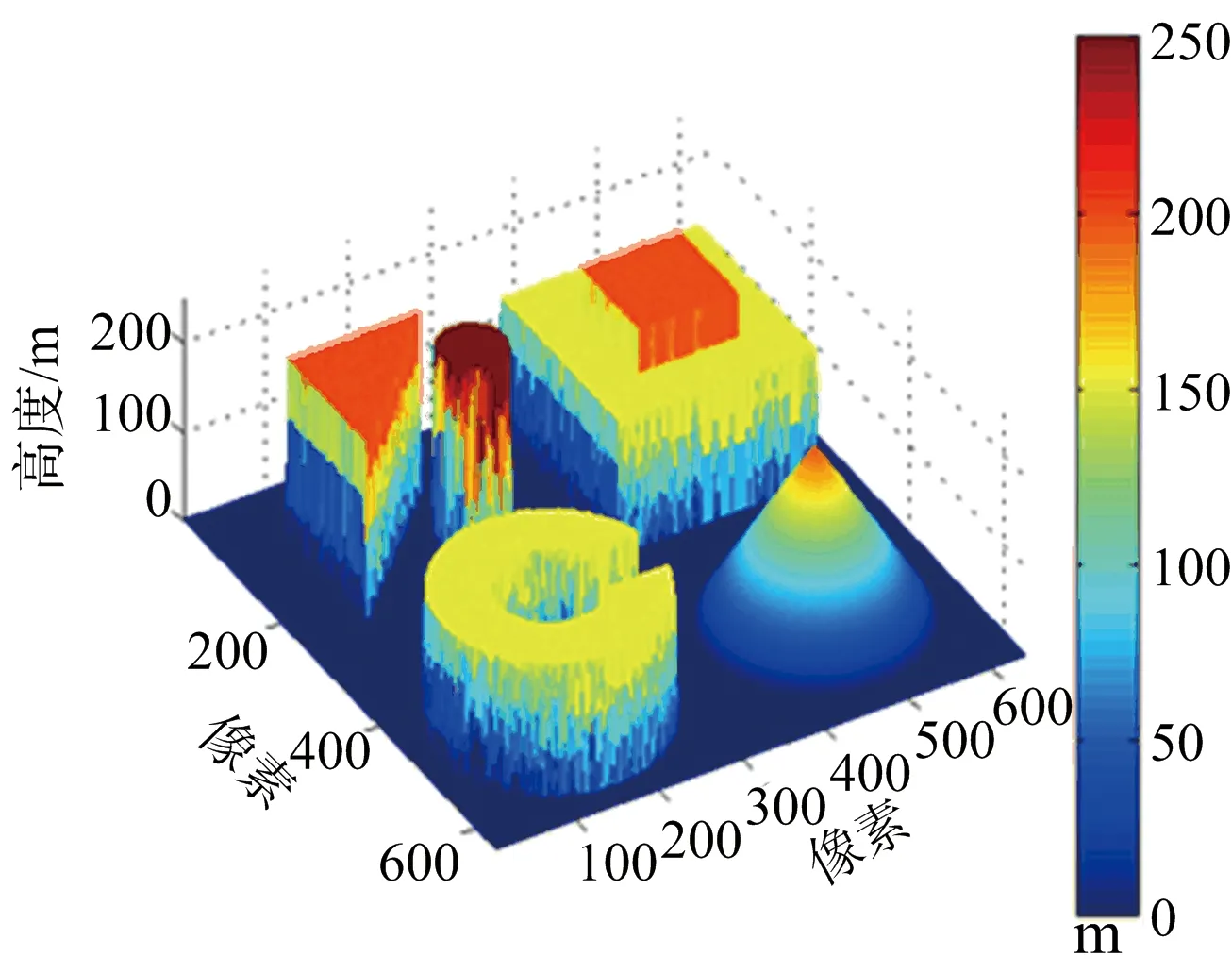
(d) 本文算法重建DEM圖6 各重建結果三維視圖
3.1.2 仿真真實地形
美國Isolation Peak國家公園DEM仿真參數如表1所示。圖7(a)為該場景的DEM投影圖。兩個通道的干涉圖如圖7(b)、圖7(c)所示。
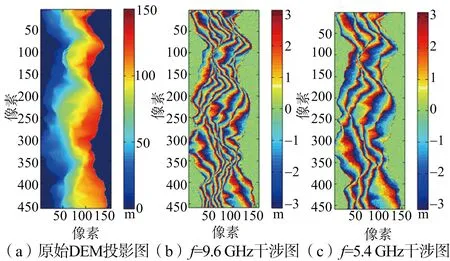
圖7 真實地形數據
進行高程反演所得的MLE結果如圖8(a)所示。對MLE結果進行噪點去除(結果如圖8(b)所示)和噪斑去除(結果如圖8(c)所示)。從結果中看出,重建的高程基本將MLE結果中的噪斑去掉。
圖9列出了各算法DEM與原始DEM。3種重建算法的誤差圖分別如圖10(a)、圖10(b)、圖10(c)所示。統計的誤差如表3所示。重建時間來看:MLE算法為2.14 s,本文方法為3.08 s,MAP估計法為258.14 s。說明本文方法可以保證重建精度和重建效率。
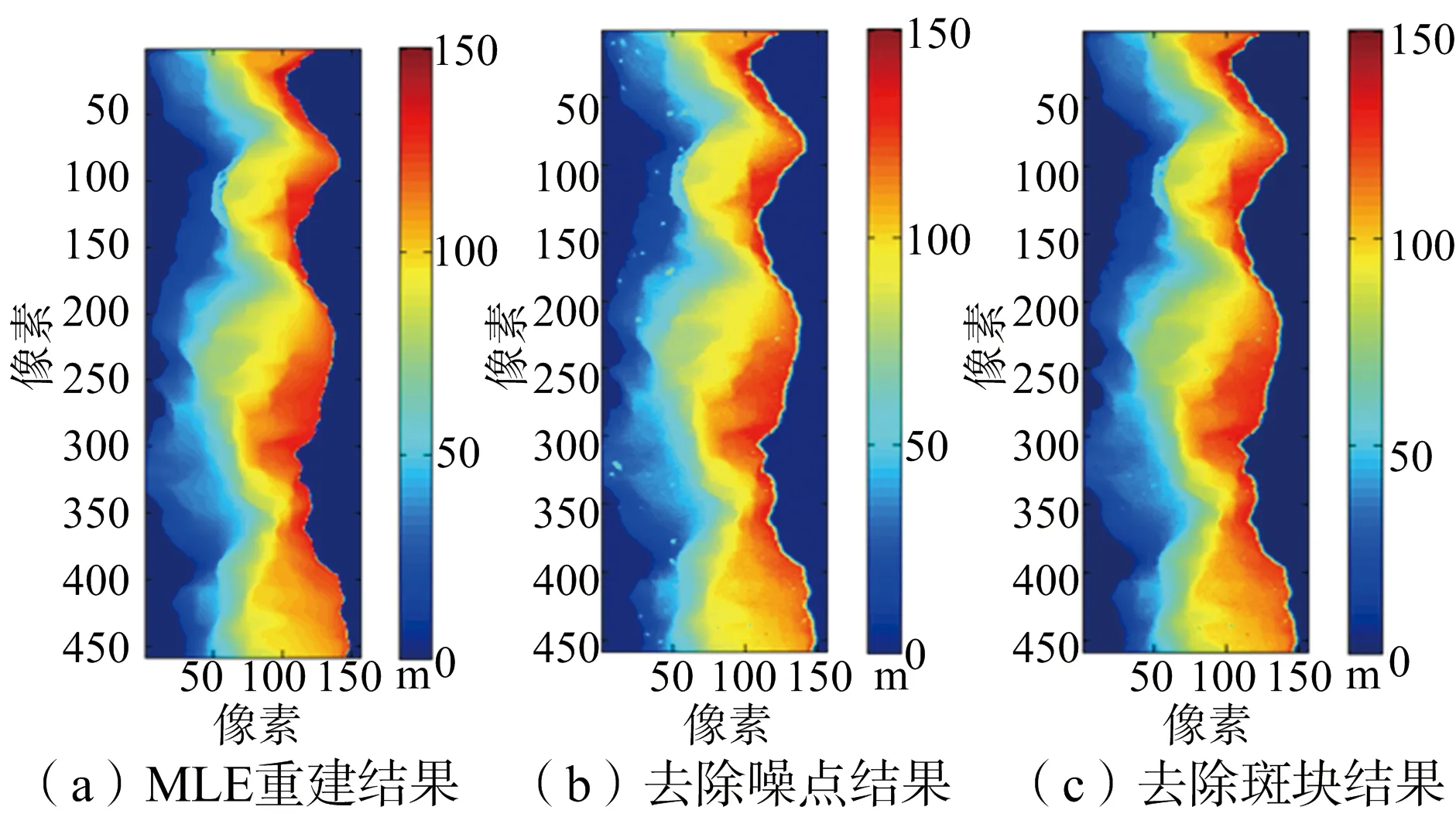
圖8 真實地形去噪
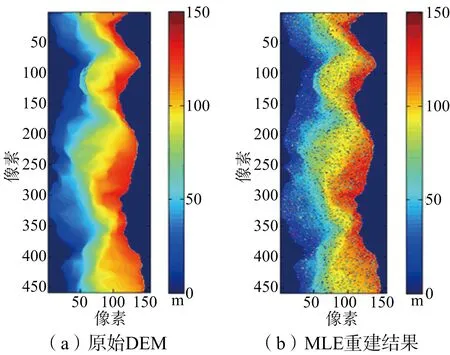
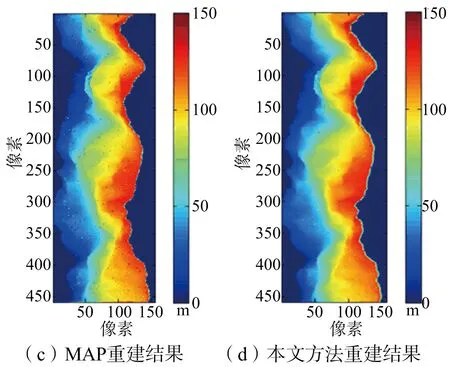
圖9 真實地形各重建結果與原始DEM對比
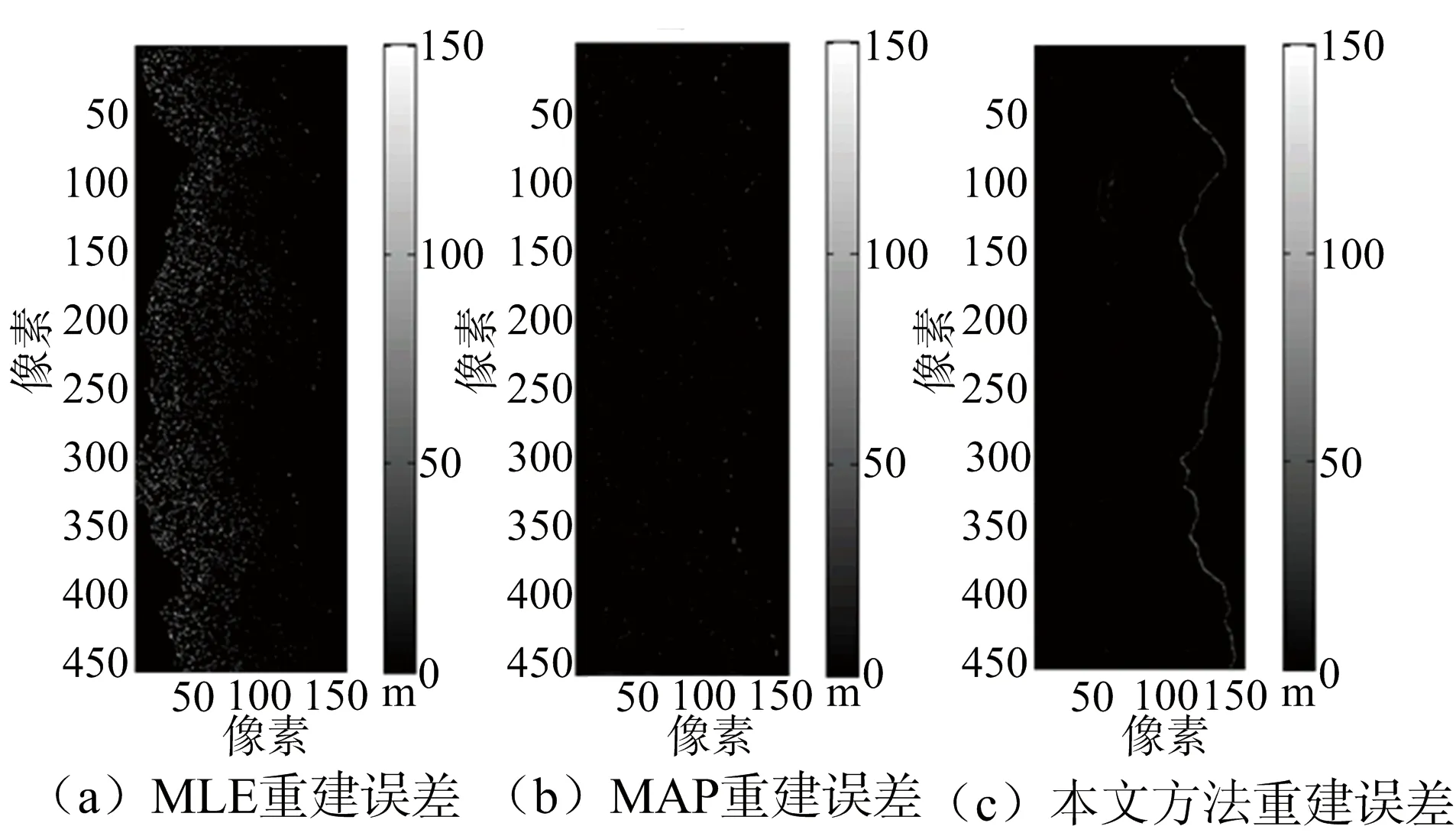
圖10 仿真城市地形各種重建算法誤差圖
圖11為各重建結果三維視圖。算法優劣此處不再贅述。

表3 真實地形重建算法歸一化均方誤差表
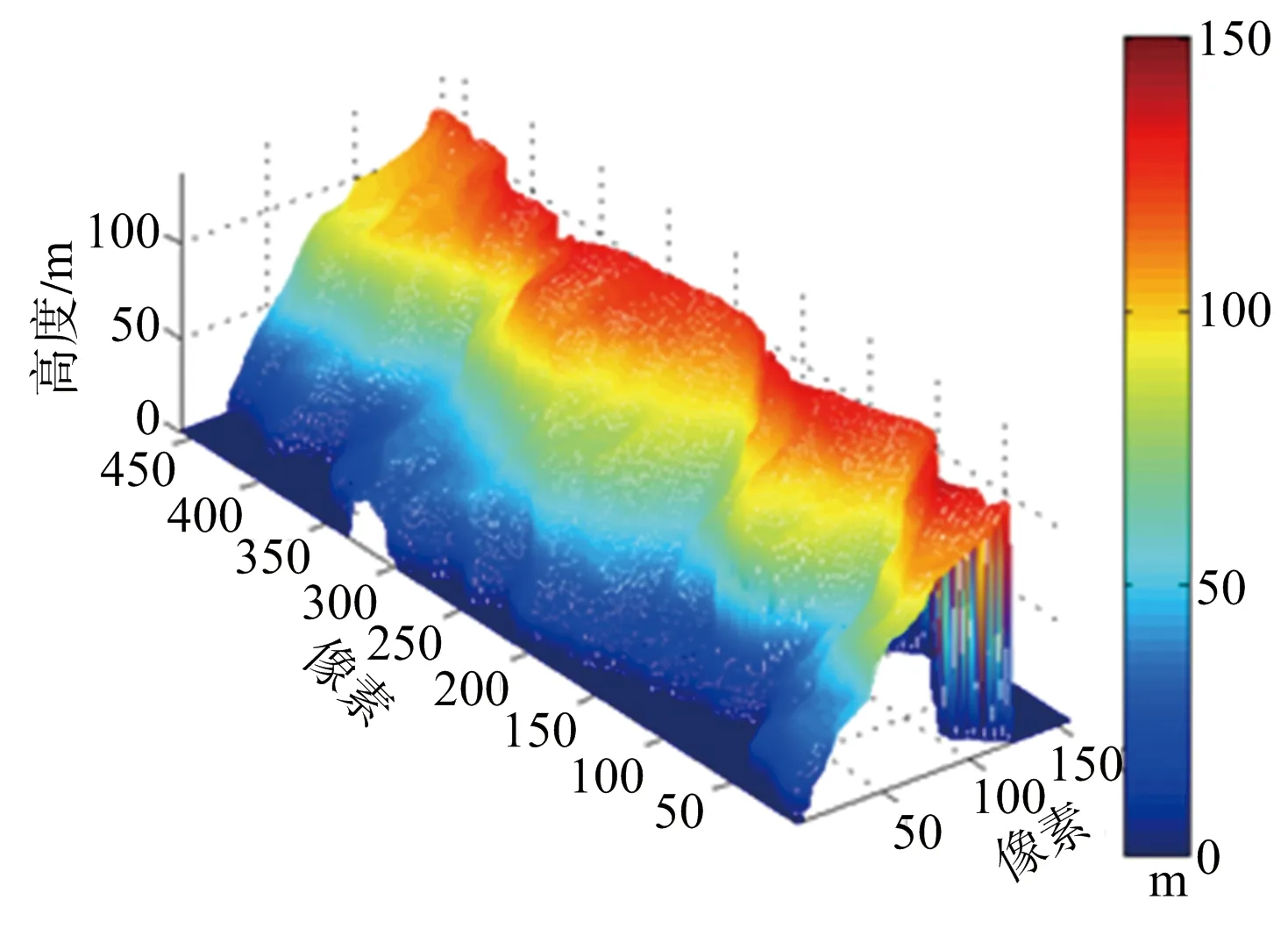
(a) 原始DEM
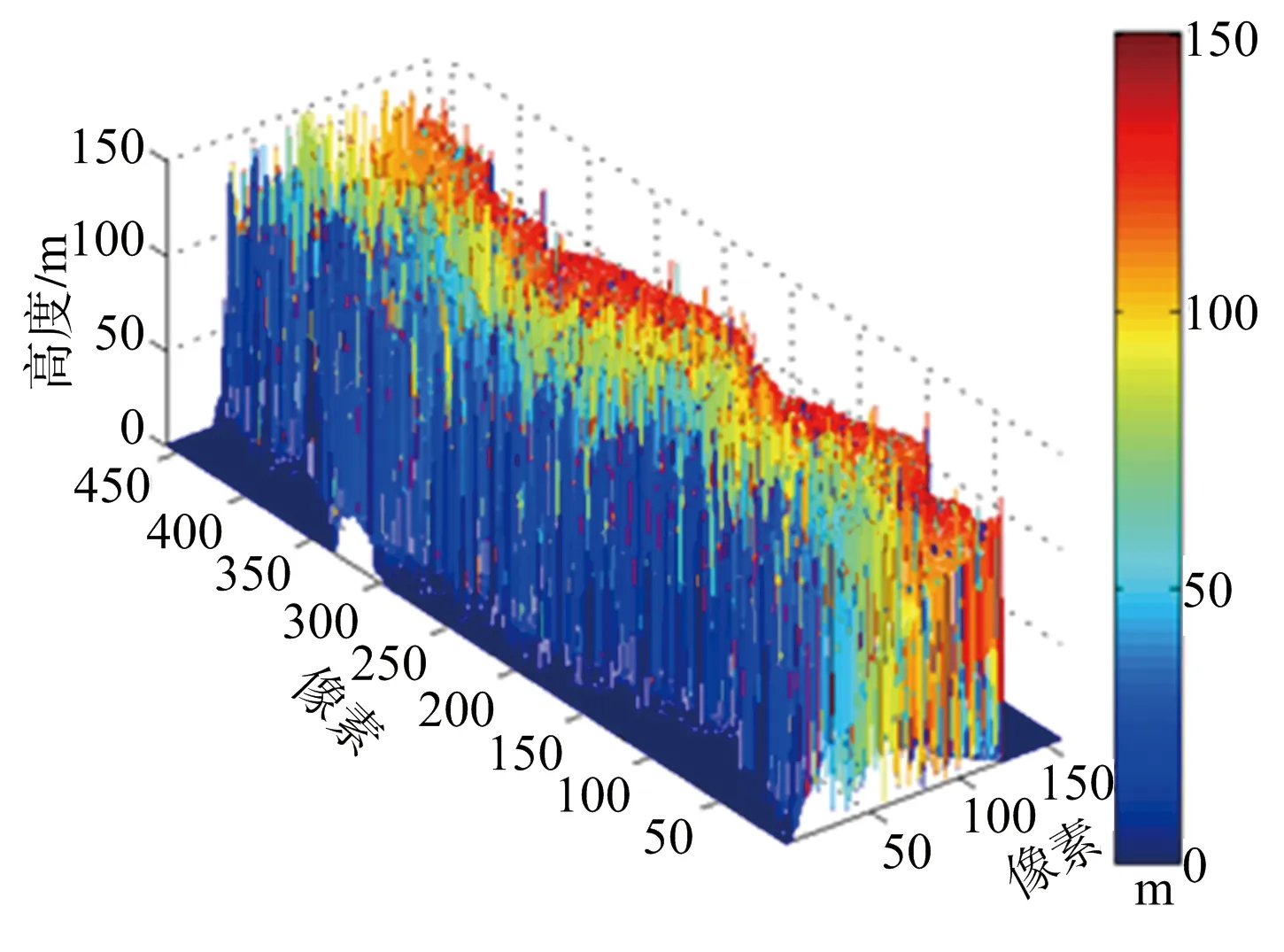
(b) MLE算法DEM
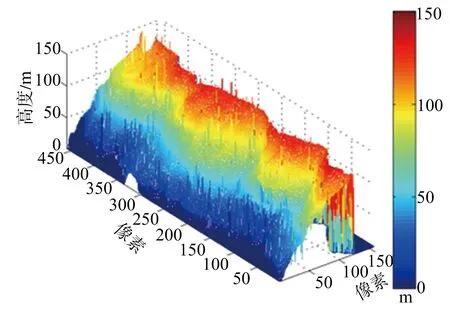
(c) MAP算法DEM

(d) 本文方法DEM圖11 各重建結果三維視圖
3.2 實測數據處理
實測數據采用了機載C/X雙頻干涉SAR測量數據,該機載平臺的具體參數如表4所示。第一塊實驗數據為澄城縣城的干涉SAR數據。縣城中高樓高度有90~100 m。兩個通道相鄰像素之間的干涉相位差分別可達3.2π和5.8π。第二塊數據為白水縣東坡村附近數據,該塊數據中有溝壑和高架橋,地形復雜多變。兩塊數據均適合驗證雙頻干涉處理算法。
表4 機載C/X雙頻系統主要參數
3.2.1 澄城縣實測數據處理
所選取的地域和對應的光學圖像如圖12所示。圖中黃色旗幟所示的點為選取的控制點。對澄城縣的兩幅C/X波段圖像分別進行配準,得到兩幅干涉條紋圖分別如圖13(a)、圖13(b)所示,利用軌道法[13]去除平地效應。再將C/X波段得到的干涉圖配準。得到配準的去平地干涉相位圖如圖13(c)、圖13(d)所示。MLE算法進行高程重建結果如圖14(a)所示,利用本文方法去噪所得結果如圖14(b)所示。圖15(a)、圖15(b)所示為重建結果的三維視圖,可以更清楚地看出本文方法的有效性。

圖12 澄城縣Google Earth光學圖像與干涉SAR數據圖像
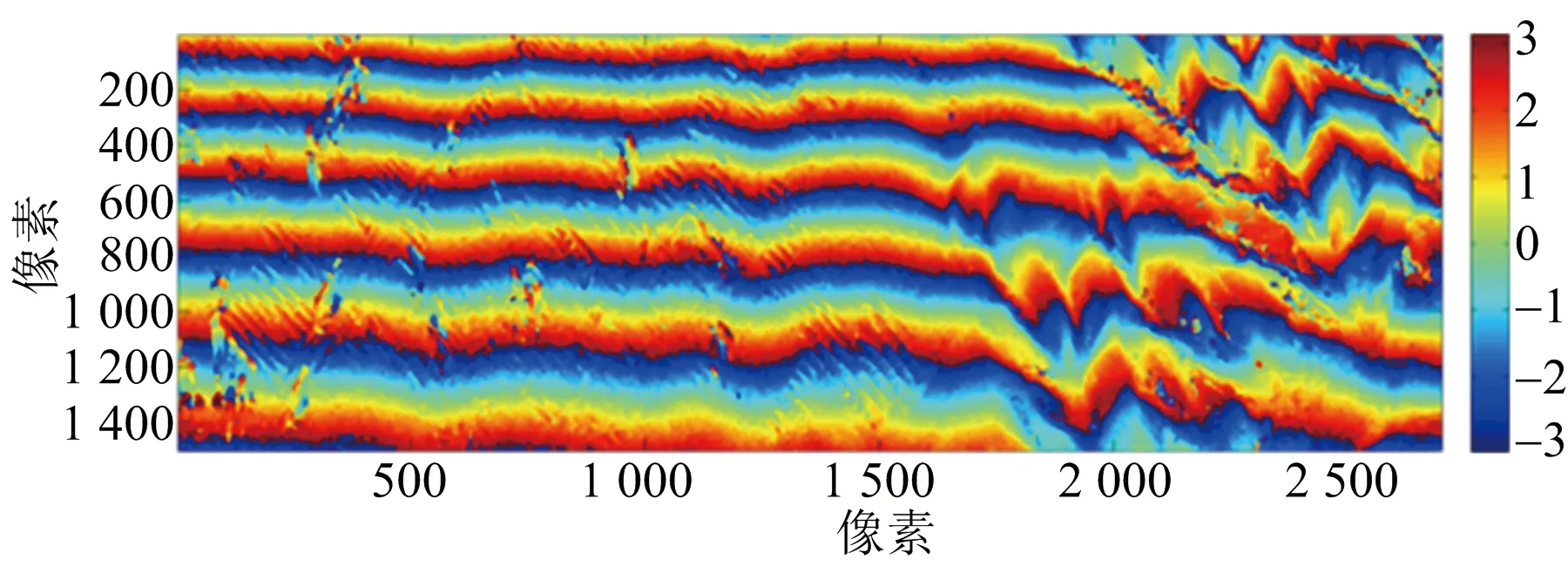
(a) C波段干涉相位圖
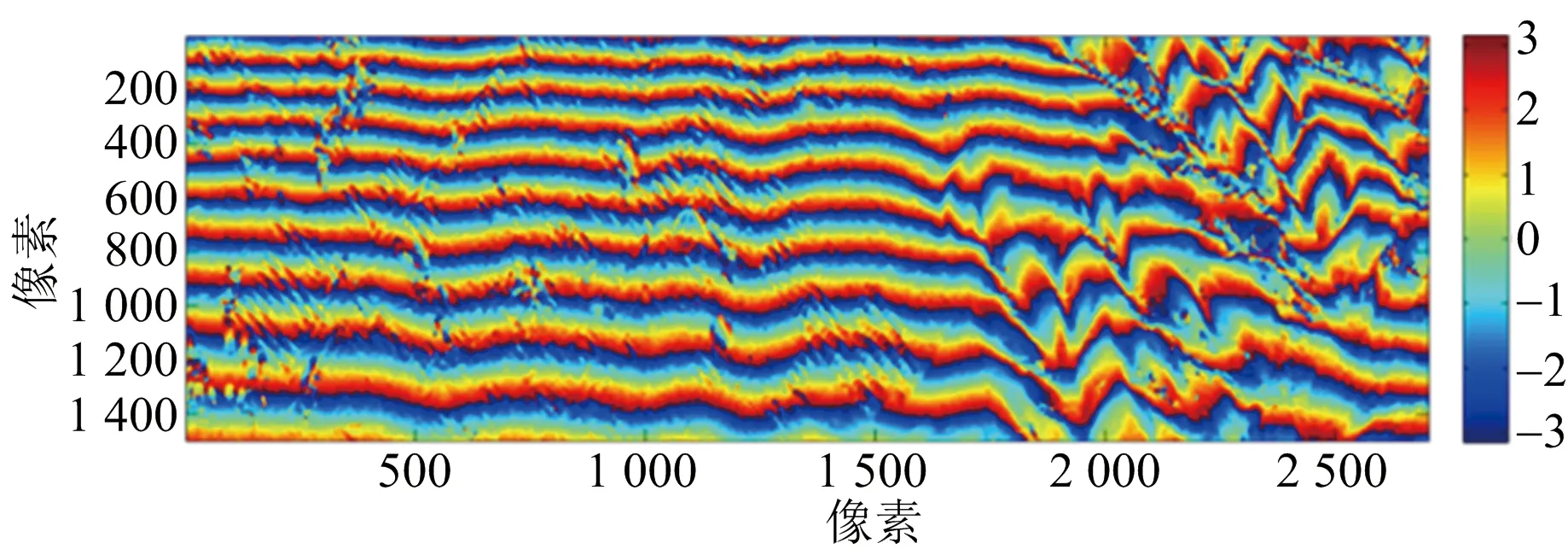
(b) X波段干涉相位圖

(c) C波段去平地干涉相位圖
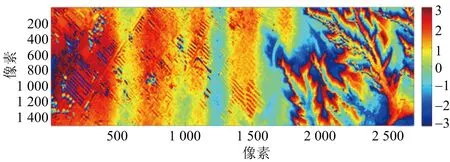
(d) X波段去平地干涉相位圖圖13 各個通道去平地前后干涉相位圖

(a) MLE重建結果
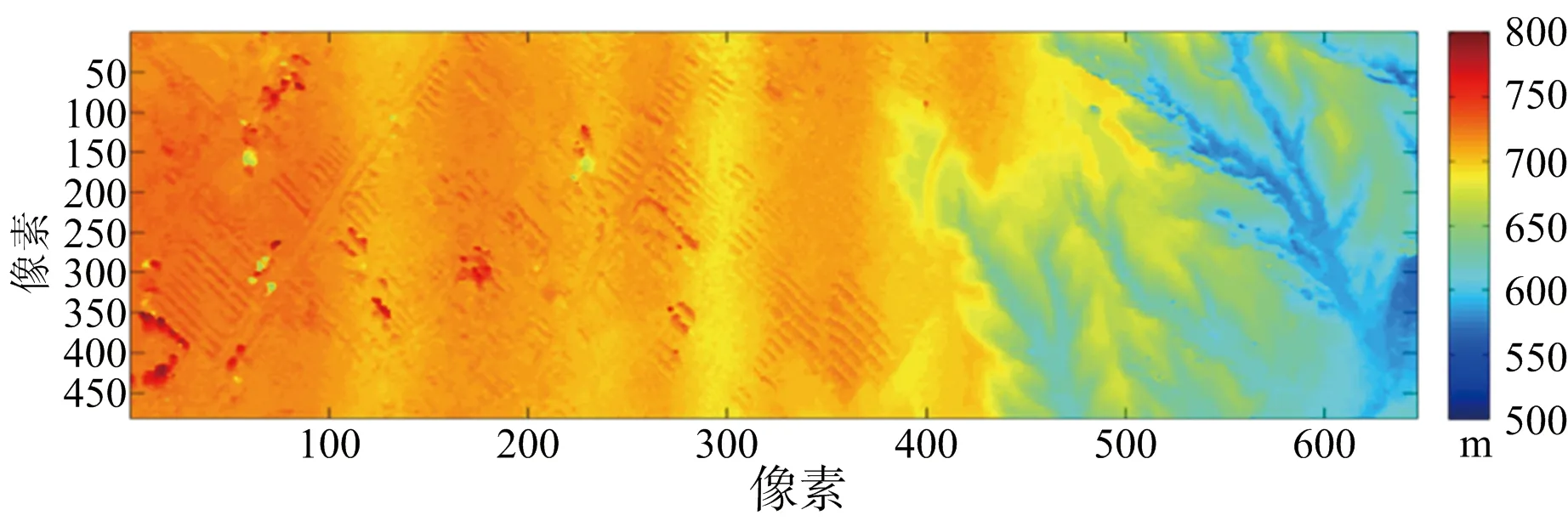
(b) 本文方法結果圖14 MLE算法重建結果與本文方法去噪結果
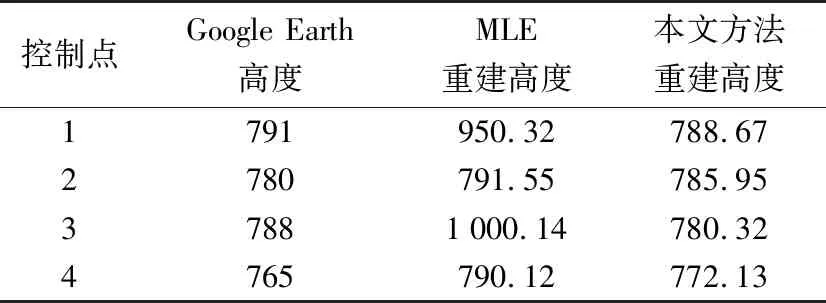
對圖12中所選取的控制點進行高程統計,統計結果如表5所示。從結果中可以看出,MLE算法噪聲過多,本文方法反演高度接近于真實高度。由于使用MAP耗時過長,這里沒有采用。
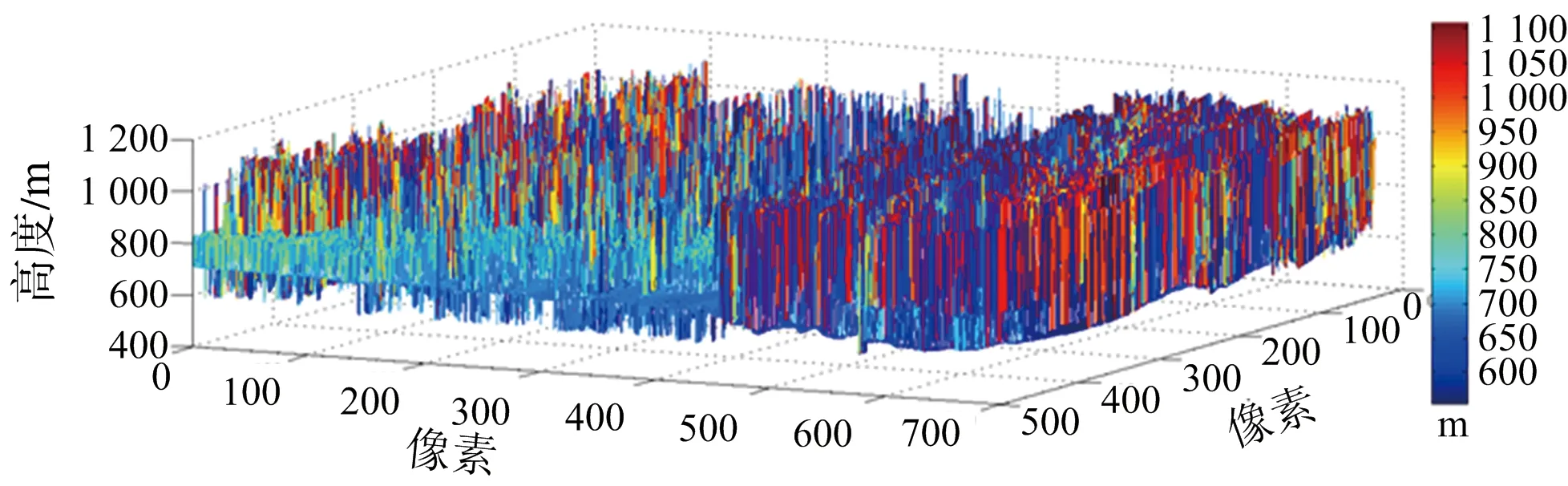
(a) MLE結果三維DEM
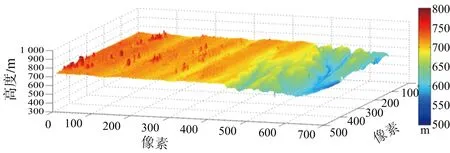
(b) 本文結果三維DEM圖15 MLE算法重建結果與本文方法去噪結果三維視圖
m
3.2.2 白水縣東坡村實測數據處理
首先給出的是光學圖像和SAR圖像如圖16所示。黃色旗幟為誤差分析控制點。其中1號點地區為溝壑,2號點白色條狀地形為高架橋的影像,3號點地區為平地上的河流。
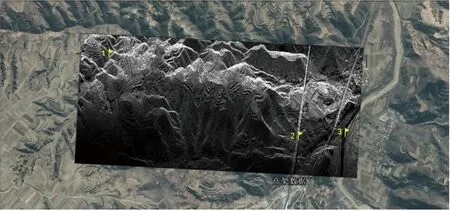
圖16 白水縣東坡村附近高架Google Earth光學圖像與干涉SAR數據圖像
兩幅干涉條紋圖分別如圖17(a)、圖17(b)所示,配準的去平地干涉相位圖如圖17(c)、圖17(d)所示。
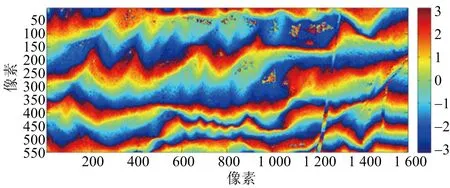
(a) C波段干涉條紋
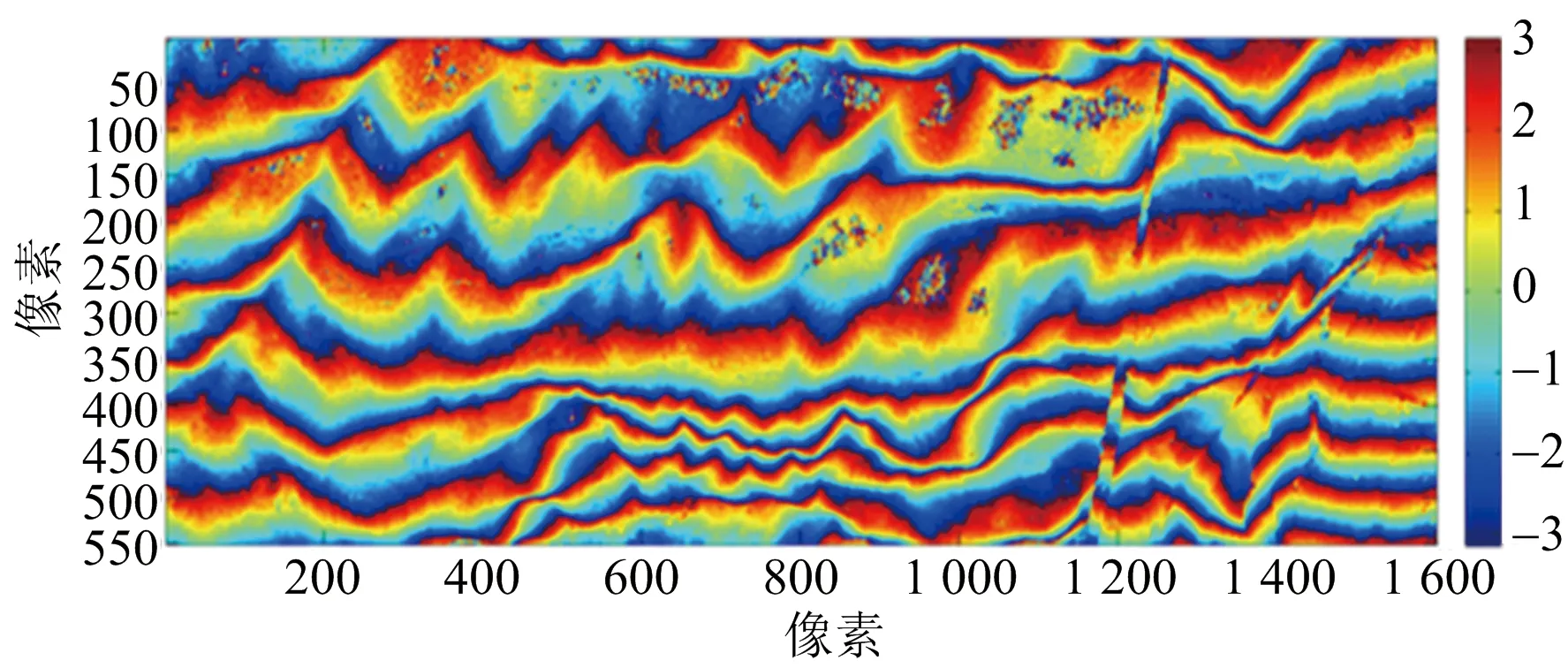
(b) X波段干涉條紋
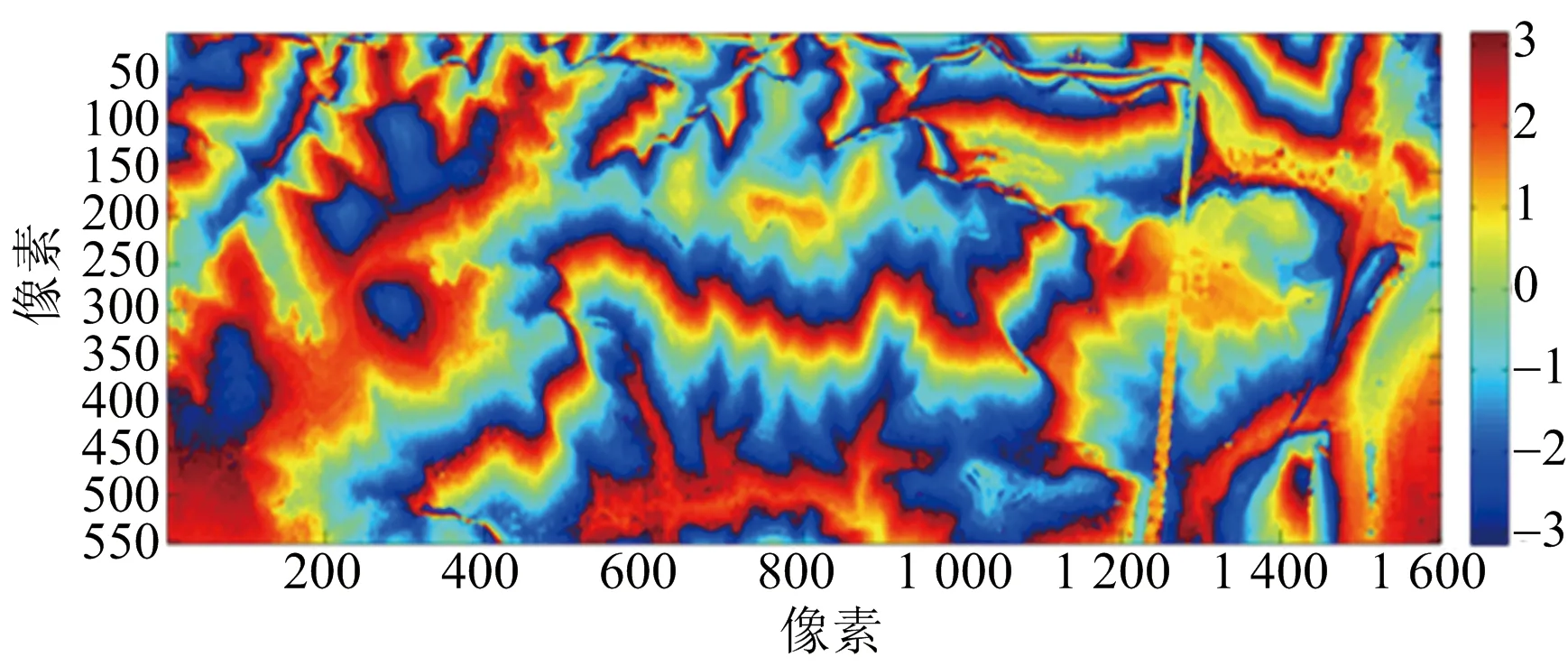
(c) C波段去平地干涉相位
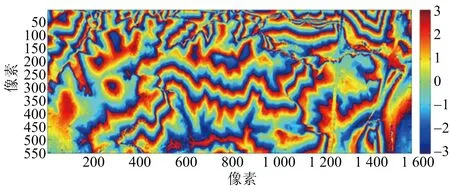
(d) X波段去平地干涉相位圖17 各個通道去平地前后干涉相位圖
MLE算法重建結果如圖18(a)所示,利用本文方法進行重建結果如圖18(b)所示。可見噪斑去除效果明顯,具有良好的重建性能。
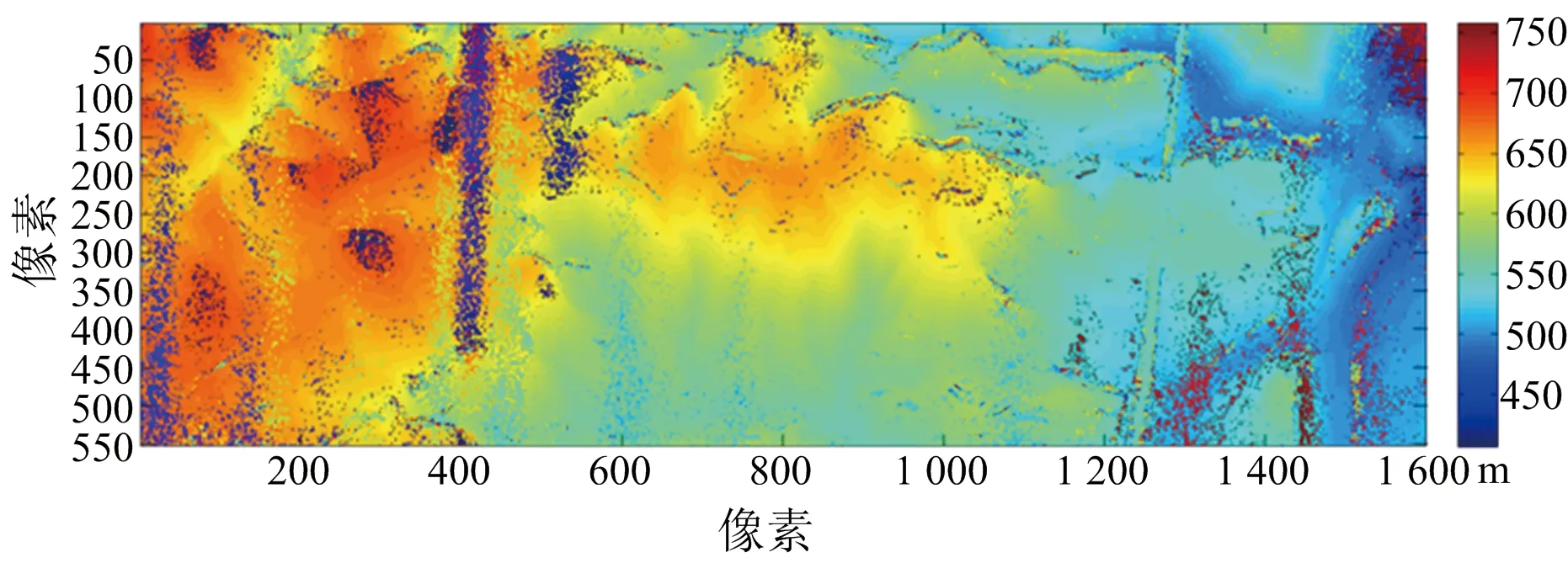
(a) MLE重建結果
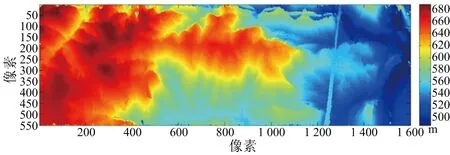
(b) 本文方法重建結果圖18 MLE算法重建結果與本文方法去噪結果
控制點高程統計結果如表6所示。在某些地帶MLE算法噪聲過大,例如本例中的3號控制點河流部分,高架邊緣部分。統計結果表明,本文方法有效提高了重建精度。
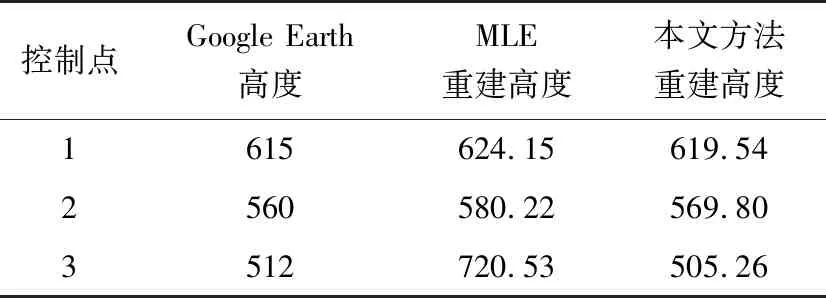
表6 控制點高度統計表 m
圖19(a)、圖19(b)列出了MLE和本文方法的重建結果三維視圖。為了減少內存消耗,在生成三維圖形時,在方位向作了降采樣處理,因而三維視圖中方位向點數變少。
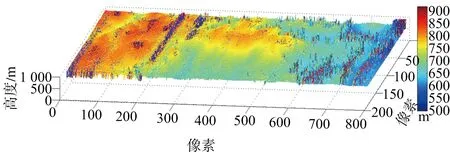
(a) MLE重建結果
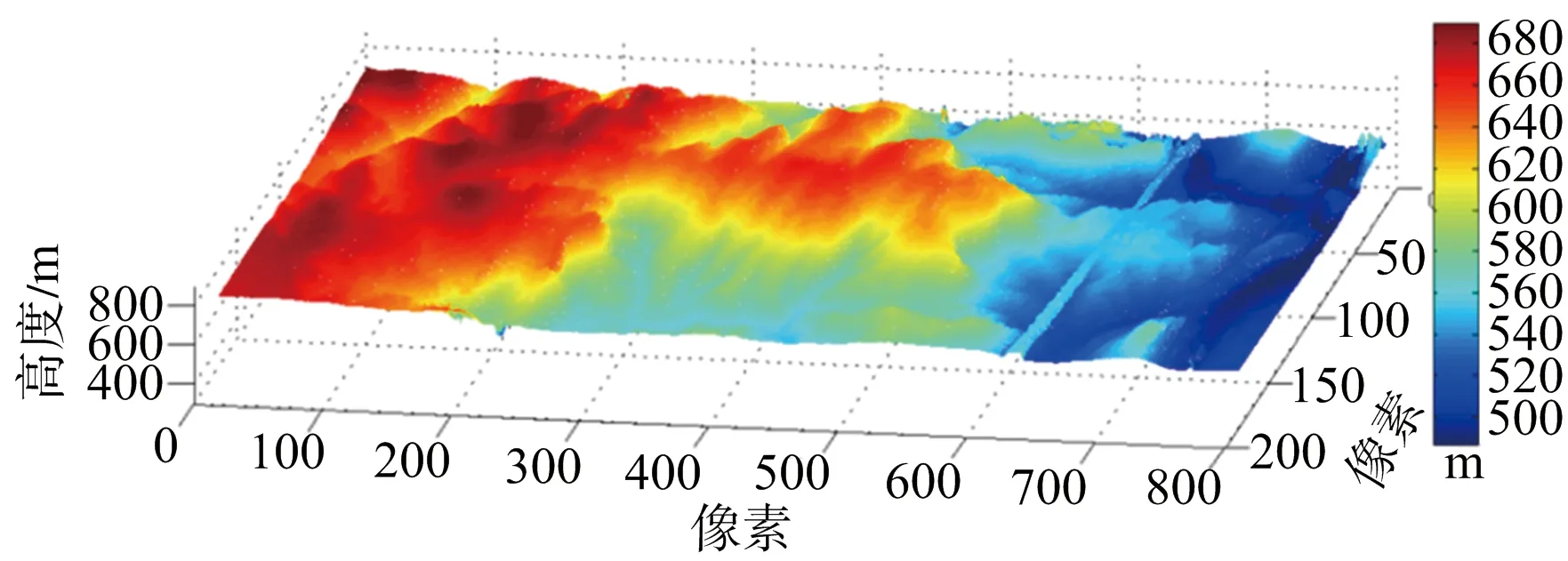
(b) 本文方法重建結果圖19 MLE算法重建結果與本文方法去噪結果三維視圖
4 結束語
本文對傳統的基于MLE的雙頻重建算法進行了改進,可以去除MLE重建結果中的噪點和噪聲斑塊,在保證重建效率的同時提高重建精度。基于上文模擬模型的論證分析,本文的方法在精度上與MAP估計相近,但是在重建效率上要遠遠優于MAP估計。上文中的實測數據處理結果表明,本文提出的方法可以用在大規模數據處理過程中,擁有較為良好的處理效果。但是本文方法也存在不足,例如閾值的選取和加權窗口的選取一般都是選取經驗值,后期需要添加自適應的閾值控制方法來降低后處理的難度。此外,更加合理的去噪權值應該為越臨近所求像素點的權值越大,越遠的像素點權值越小,這也是以后工作中一個要調整的方面。

