基于三維加速度橢球法的液貨艙內部壓力解析算法

付喜華

(中國船級社 規范與技術中心， 上海200135)

0 引 言

2016年生效的《國際散裝運輸液化氣體船舶構造與設備規則》(InternationalCodefortheConstructionandEquipmentofShipsCarryingLiquefiedGasesinBulk，下文簡稱IGC 規則)[1]在圍護系統載荷計算方法上作了重要修改，即考慮船舶縱向運動產生的縱向載荷的影響，用三維加速度橢球法替代了上一版IGC 規則中的二維加速度橢圓法。各船級社液化氣體船規范指南也根據新IGC 規則進行了更新[2-4]。使用三維加速度橢球法計算液貨艙內部壓力，增大了計算難度，但得到的載荷結果更加接近船舶實際情況，更趨于合理。

現行的迭代法計算液貨艙內部壓力基于對橢球法定義的任意空間角度(兩個維度)的迭代數值計算法開展[5-6]，需要完成兩個空間維度的反復迭代。運算次數與迭代步數的平方成正比，計算效率較低，且計算結果的精確度受設置兩個角度的迭代步長影響。

為了改善上述迭代法的不足，提升計算效率和精度，基于新IGC 規則中的加速度橢球分析法，通過構造三維坐標系，依據立體幾何和三維向量理論，推導任一計算點基于液貨艙邊界某一特定點的內部壓力的解析解表達式，并編制迭代法數值計算程序。通過實例計算比較上述兩種方法的計算結果。

1 新IGC 規則內部壓力計算規則

根據新IGC 規則[1]的描述，液貨艙內部壓力由設計蒸氣壓力P0和艙內液體貨物運動產生的壓力Pgd兩部分組成。Pgd的計算尤為關鍵，可由下式計算得到

(1)

式中：ρ為液貨的密度；aβ為在任意的β方向上，由重力和動載荷引起的無因次加速度；zβ為從計算點到液貨艙邊界上高于計算點的各點在方向β上的液貨高度，m。其中，β為加速度橢球內任意無因次加速度與重力加速度的合成加速度方向，動載荷引起的加速度由加速度橢圓或橢球決定。

aβ縱向、橫向和垂向的最大加速度分量axx、ayy和azz在IGC 規則中有明確的簡易計算方法。新IGC 規則給出了顯示最大加速度分量的三維加速度橢球示例[1]，如圖1所示。zβ計算示例如圖2所示。

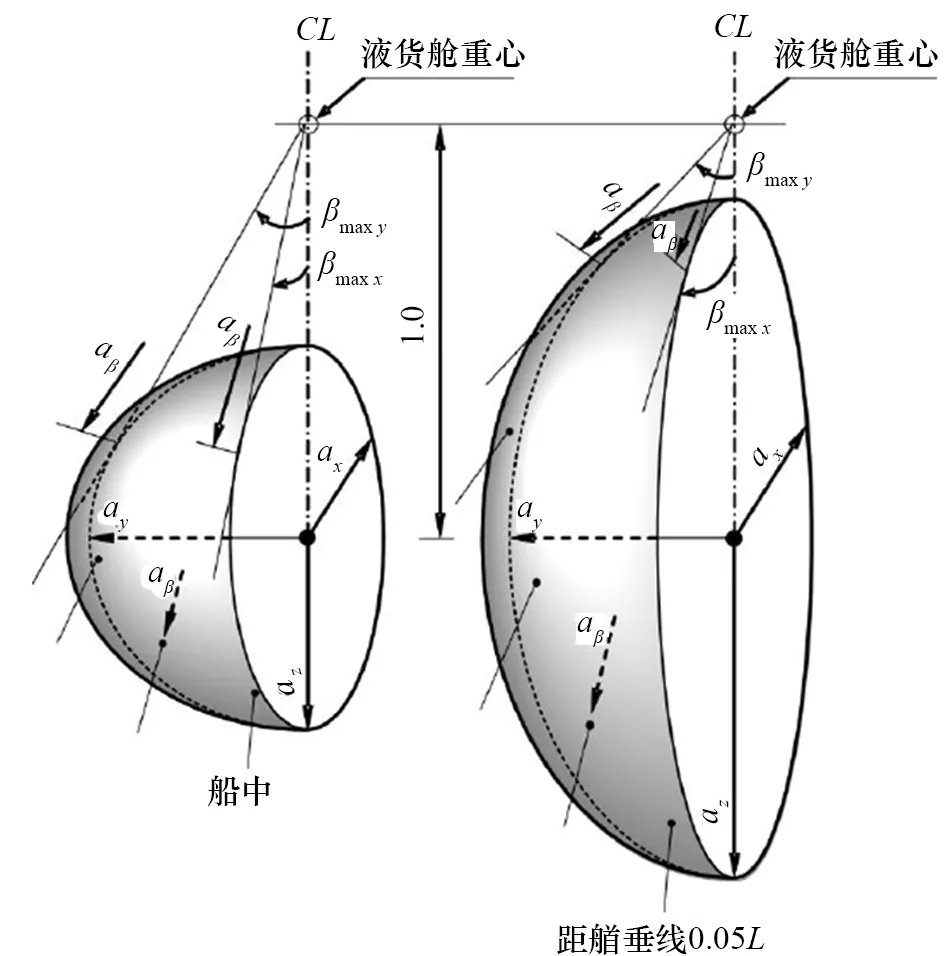
圖1 加速度橢球

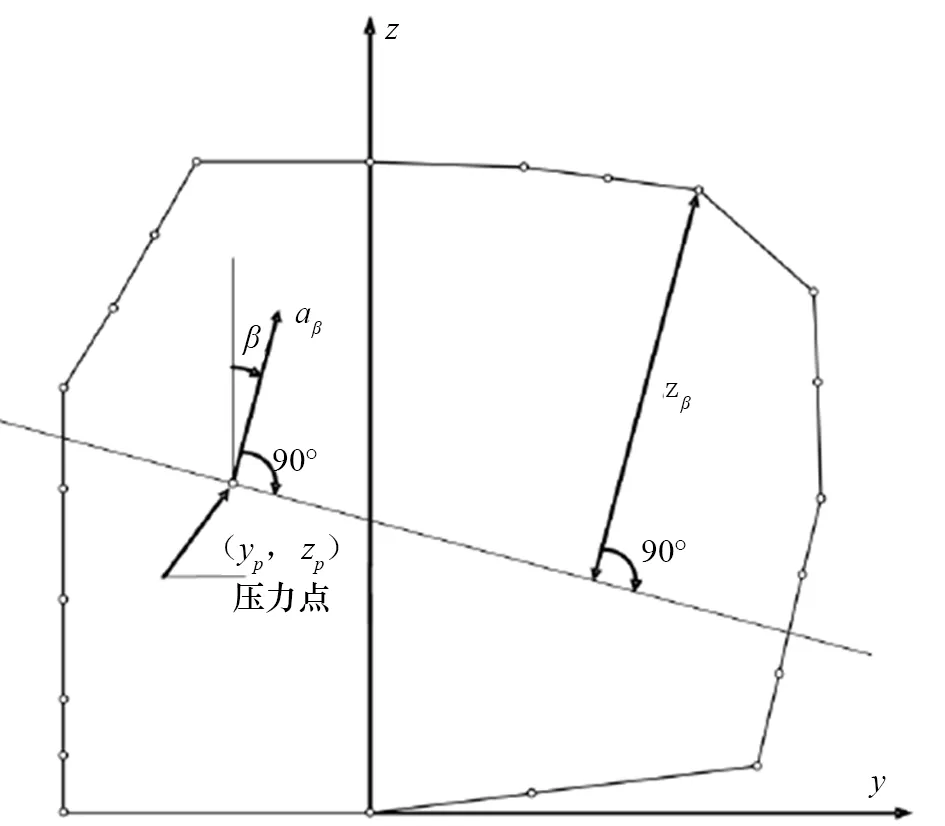
圖2 zβ計算示例

2 加速度橢球迭代計算法

采用基于新IGC 規則的加速度橢球迭代法計算的原理是：通過設定縱向和橫向兩個方向的迭代角度α(i)和γ(j)，在任意加速度方向上開展內部壓力的迭代計算，完成整個加速度橢球的搜索后確定內部壓力的極大值[5]。加速度橢球迭代法如圖3所示。

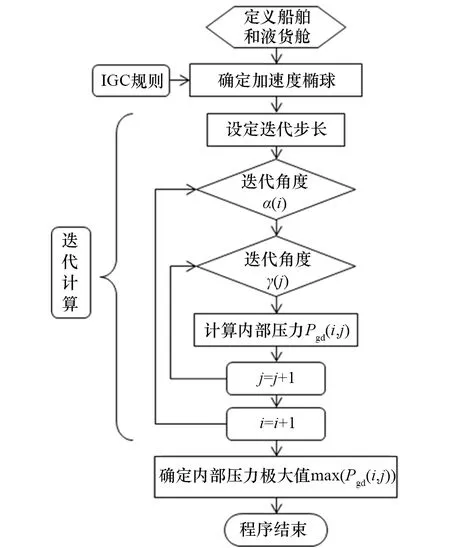
圖3 迭代計算法流程

迭代法需通過反復迭代完成基于任意加速度方向的內部壓力數值計算，過程繁冗，運算次數是解析解法的千倍，計算時間較長；不同的程序設計開發人員對迭代步長α(i)和γ(j)的設定不同，沒有統一的標準；設定較大迭代步長影響計算結果的精確度，而較小的步長將大幅增加計算時間，影響計算效率。

3 加速度橢球解析計算法

建立如圖4所示的坐標系：以液貨艙加速度橢球的中心為原點建立空間坐標系，船長方向為x坐標軸(船首方向為“+”)，船寬方向為y坐標軸(左舷為“+”)，型深方向為z坐標軸(向上為“+”)。

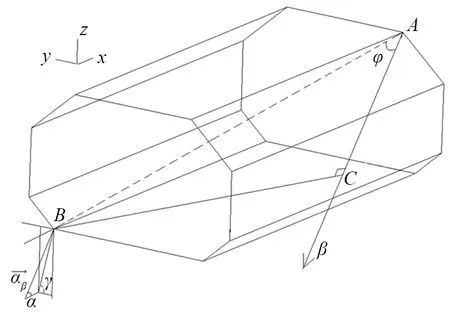
圖4 參考液貨艙邊界及坐標系

液貨艙邊界特定點A的坐標為(x0、y0、z0)，計算點B的坐標為(x1、y1、z1)，得到

AB=(x1-x0,y1-y0,z1-z0)

(2)

通過A點沿加速度β方向做1條直線，B點在該直線上的投影為C點，φ為AB與AC的夾角，可得|AC|即為A點到計算點C點在方向β上的液貨高度zβ：

zβ=|AC|=|AB|×cosφ

(3)

加速度橢圓參數方程可表示為

(4)

式中：α為加速度與x軸的夾角；γ為加速度在yOz面上的投影與y軸的夾角，如圖4所示。

上述加速度與重力加速度合成，即可得

aβ=(axxcosα,ayysinαcosγ，

-1+azzsinαsinγ)

(5)

加速度αβ與在方向β上液貨高度zβ的乘積可表示為

αβzβ=|aβ|×|AC|=|aβ|×|AB|×cosφ

(6)

根據向量的數量積理論可知

aβ·AB=|aβ|×|AB|×cosφ

(7)

由式(6)、式(7)可以得出：

αβzβ=aβ·AB

(8)

將式(2)、式(4)代入式(8)，依據向量數量積算法可得

αβzβ=ax×(x1-x0)+ay×(y1-y0)+

(-1+az)×(z1-z0)

(9)

將式(4)、式(5)代入上式(9)，得到

αβzβ=axx(x1-x0)cosα+ayy(y1-y0)·

sinαcosγ+azz(z1-z0)sinαsinγ-(z1-z0)

(10)

式(10)可以表達為

αβzβ+(z1-z0)=acosα+bsinαcosγ+csinαsinγ

(11)

式中：

(12)

將式(11)、式(12)定義的橢球參數方程轉換成標準方程，可以得到

αβzβ+(z1-z0)=x+y+z

(13)

(14)

顯然，αβzβ+(z1-z0)的極大值可以理解為式(14)表示的橢球與式(13)表示的空間平面相交或相切情況下形成的平面與原點之間距離的極大值。

通過三維立體幾何知識及運算可得到

(αβzβ)max=-(z1-z0)+

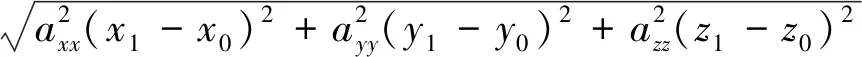
(15)

根據三角函數算法，式(15)達到極大值時，α、γ滿足以下條件

(16)

(17)

將式(15)代入式(1)中，即可得到基于某一特定點的內部壓力的解析計算公式為

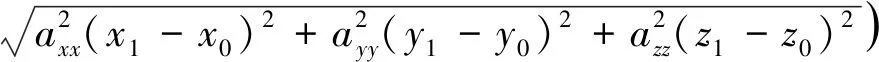
(18)

加速度橢球形解析法流程如圖5所示。

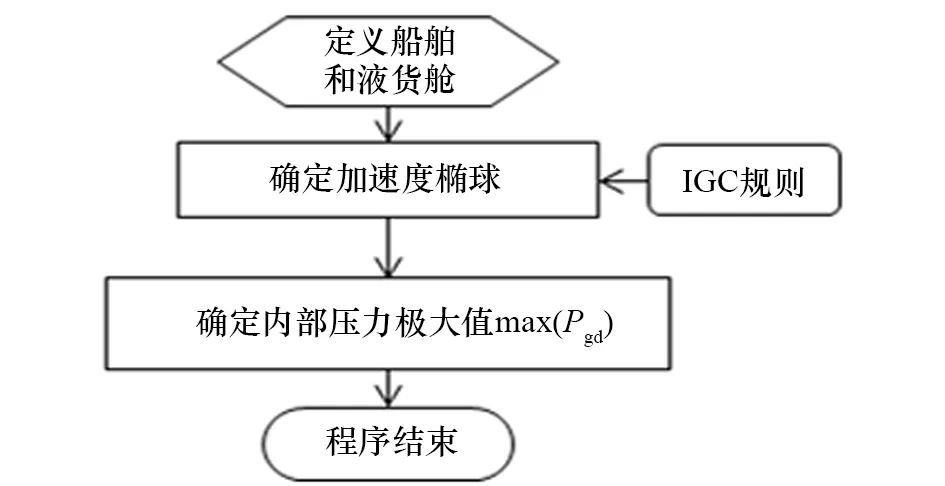
圖5 加速度橢球形解析法流程

4 算 例

為了驗證上述推導的準確性以及比較解析解法與迭代法的差異，編制迭代算法計算程序，對某薄膜型LNG運輸船某液貨艙進行Pgd的迭代計算，并將計算結果與基于加速度橢球解析法的計算結果進行比較。為了保證計算精度，加速度橢球角度迭代步數分別設定為40(縱向)和100(橫向)。圖6所示為薄膜型LNG船的液貨艙邊界及邊界上的10個計算點。

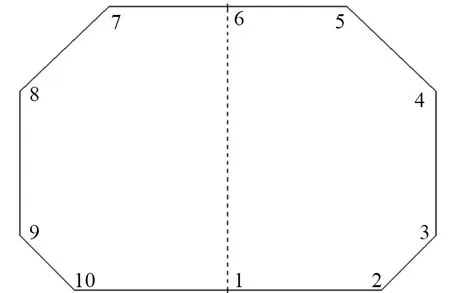
圖6 液貨艙邊界計算點

對圖6所示液貨艙分別采用解析法和迭代法得到圖示10個計算點的Pgd計算結果，如表1所示。

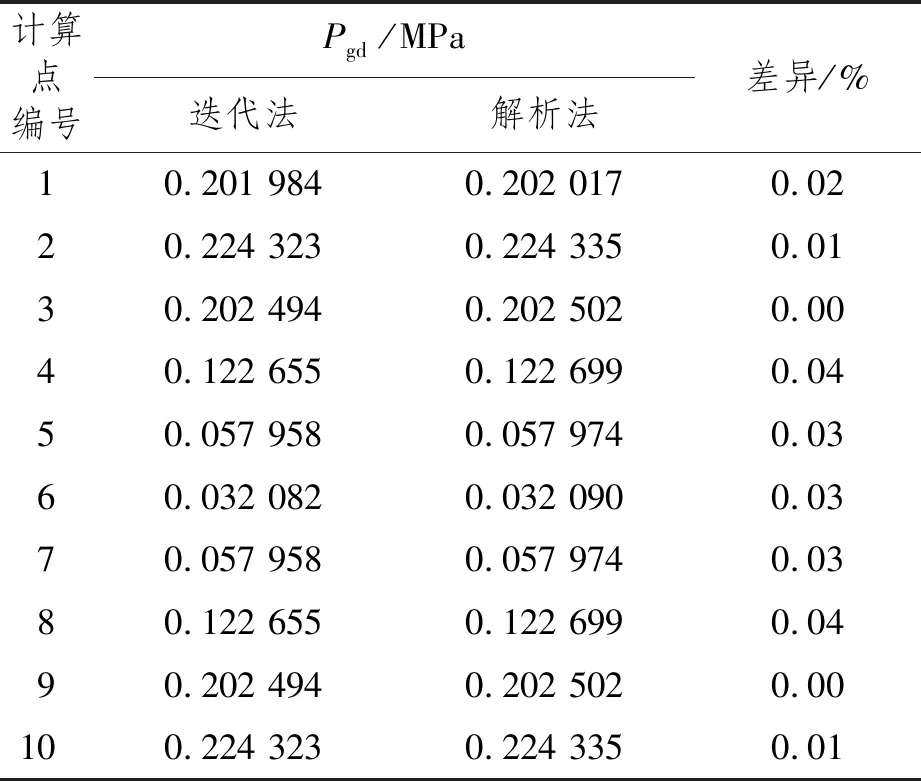
表1 解析法與迭代法(加速度橢球法)計算結果比較

從表1可以看出，解析法和迭代法的計算結果呈現以下特征：

(1) 解析計算的結果微大于迭代計算的結果，符合解析解為極大值的客觀實際；

(2) 由于選取的角度迭代步長較小，縱向和橫向迭代次數分別為40次和100次，迭代步長小于1°，精度得到了很好的控制，迭代計算結果與解析算法結果非常接近。

分別采用加速度橢球法和加速度橢圓法對圖5所示計算點進行Pgd計算。表2比較了計算結果差異，可以看出：

(1) 由于橢球法考慮了船舶縱向運動產生的載荷影響，計算結果略大于橢圓法的結果，除了內甲板外，相差最大處不大于4%；

(2) 由于內甲板位置處縱向運動產生的載荷在內部壓力中占比較其他位置大，所以在點6處兩種方法的計算結果差異較大。

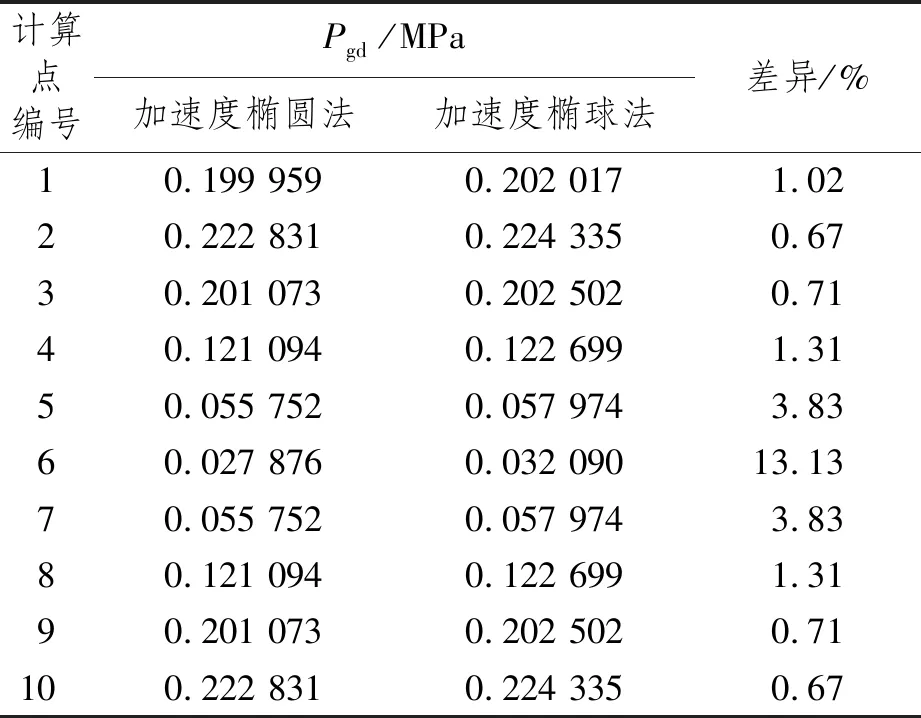
表2 加速度橢圓法與加速度橢球法(解析法)計算結果比較

最后，對基于上述3種方法完成的液貨艙10個計算點的Pgd計算所花費時間分別進行了統計，如表3所示。

表3 3種計算方法的計算時間 s

由表3可以看出：

(1) 解析法的計算效率遠遠高于迭代法，計算時間僅為迭代法計算時間的1/1 063；

(2) 三維加速度橢球法與二維加速度橢圓法計算效率相近，計算時間相近。

5 結 論

通過基于橢球法的內部壓力解析解的理論推導，

以及實例計算驗證，得出加速度橢球解析算法具有計算結果準確、運算效率高、簡單易用的優點，為設計人員開展內部壓力計算及其液貨艙結構尺寸設計提供重要幫助和依據。