探究幾類遞推數列的解題方法和技巧

貴州省畢節市赫章縣第一中學 顧開鵬

一階遞推數列定義：對于任意n∈N+，由遞推關系an+k=f（an+k-1，an+k-2，…an）確定的數列｛an｝稱為遞推數列（或遞歸數列），k為階數。若f是線性的，則稱此數列為線性遞推數列，否則稱為非線性遞推數列。

以下就介紹幾種一階遞推數列的種類，并分析了求相應遞推數列通項公式的方法。

一、一階線性遞推數列

本節闡述兩種常見的一階線性遞推數列：

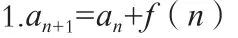
與等差數列求通項公式的方法相同，這類遞推數列通項公式求解方法依然沿用疊加法。

例1：數列{bn}中，b1=2，bn+1=bn+cn（c是常數），且b1，b2，b3成公比不為1的等比數列。

（1）求c的值；

（2）求{bn}的通項公式。

解：（1）由題可知：b1=2，b2=2+c，b3=2+3c，因為b1，b2，b3成公比不為1的等比數列，所以（2+c）2=2（2+3c），解得c=0或c=2。

當c=2時，b1=b2=b3，不合題意，舍去，所以c=2。

（2）當n≥2時，由于b2-b1=c，b3-b2=2c，……bn-bn-1=（n-1）c，所以

又b1=2，c=2，故bn=2+n（n+1）=n2-n+2（n=2，3，……）。

當n=1時，上式同樣成立，所以bn=n2-n+2（n=1，2，……）。

【類型評注】

求解這種類型的數列通項公式的方法叫作“疊加法”，這種方法是由高中數學教材中等差數列通項公式的求法演變而來的，將等差數列的遞推式 an-an-1=d 拓展到 an-an-1=f（n），只要 f（0）+f（2）+f（3）+…+ f（n-1）是可求的，就可以由恒等式an-an-1= f（n）以n=1，2，3，…，n-1代入，得到（n-1）個等式，再將其累加而求an。

2．an+1=pan+q（pq（p-1）≠ 0）

在高考數學考卷中，這是一種較為常見的遞推數列類型題，本節運用兩種方法解出典型例題的通項公式。

定理（1） 已知遞推數列a1=a，an+1=pan+q（pq（p-1）≠0），則通項公式為：an=[apn+（a-q）pn-1-q]/（p-1）。

以上定理的證明過程如下：

由an+1=pan+q（n≥1）得an=pan-1+q（n≥2），

所以an+1-an=p（an-an-1）（n≥2）。

所以數列{an+1-an}是首項為a（p-1）+q、公比為p的等比數列，由等比數列的通項公式可證。

我們可以利用初等代數中構造法的思想，通過設定一個待定系數來構造一個全新的等比數列，并求解出待定系數，從而借助等比數列的形式來求解出題目中原先的遞推數列的通項公式。

解：由題可知：

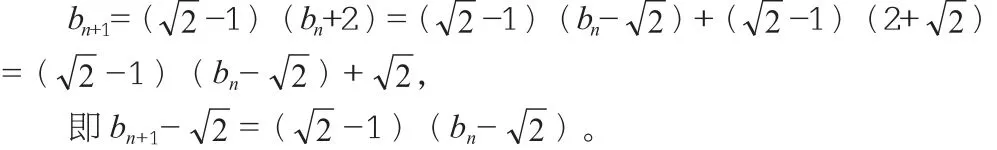
所以，數列{ bn-}是首項為2-，公比為-1的等比數列，所以bn-=（-1）2，即bn的通項公式為bn=[（-1）n+1]。

【類型評注】

本題將構造法簡化，我們就可以得出特征方程法，特征方程法將很多煩瑣的推導計算過程都省略掉了，在縮短解題時間的同時，在很大程度上也避免了解題過程中出現錯誤的幾率。

定理（2） 已知a1=a，an+1=pan+q，其中pq（p-1）≠0，稱方程x=q+px為數列{an}的特征方程，設特征方程的根為x'（x'稱為不動點），則有：

①當x'=a1時，數列{an}為常數列，an=a1；

②當x'≠a1時，數列{an-x'}是公比為p的等比數列，通項公式為：an=[apn+（a-q）pn-1-q]/（p-1）。

二、一階非線性遞推數列

一階非線性遞推數列主要包括以下幾種類型，本節通過對這幾種類型的典型例題進行求解來分析其通項公式。

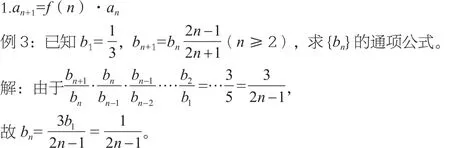
【類型評注】

求解這種類型的通項公式的方法叫作“乘積法”，這種方法是由高中數學教材中等比數列通項公式的求法演變而來的，將等差數列的遞推式拓展到，只要 f（0）·f（2）·f（3）·…·f（n-1）是可求的，就可以由恒等式以 n=1，2，3，…，n-1代入，得到（n-1）個等式，再將其乘積而求an。

2．an+1=f（n）+pan且 p（p-1）≠ 0，f（n）≠ c

bn，an2+bn+c（a≠0），kn+b（kb≠0）這三種形式是f（n）的常見形式。

例4：已知b1=1，bn+1=2an+3n-1，求{ bn}的通項公式。

解：首先構造出形式為{bn-αn-β}形式的等比數列，

使 bn+1-α（n+1）-β=2（bn-αn-β），

對應系數相等，所以α=-3，β=-2。

所以bn=5·2n-1-3n-2。

本文著重介紹了一階遞推數列求通項公式的方法，希望讀者可以通過本文提出的例題并加以聯系。相信在今后解題的過程中，可以準確快速地推導出相應遞推數列的通項公式，并且通過本文對特征方程法和構造法的介紹與比較，我們也可以了解到這兩種方法都是依托待定系數法推導出相應的通項公式。當然，當我們遇見不同類型的遞推數列時，仍然應該選用最適合的方法解答題目。另外，采用其他方法對結果進行驗證也是保證題目解答正確的有力措施。