基于盒粒子濾波的多擴展目標伯努利濾波算法

趙小龍

(安徽工業經濟職業技術學院計算機與藝術學院，安徽 合肥 230051)

0 引言

多目標跟蹤是指通過對傳感器得到的量測數據進行處理，以實現對目標個數和狀態的持續估計。作為一項關鍵技術，在諸如機器人、監控、自動駕駛、自動化和傳感器網絡中都有著廣泛的應用。

傳統的目標跟蹤均采用點目標模型，并且在大量的實際應用場景中，這種假設也是合理的。然而由于傳感器技術在近年來的快速發展，目標占據著越來越多的分辨單元，如在移動機器人和自動駕駛中，點目標的假設便難以適用。對此，我們將占據多個傳感器分辨單元的目標稱為擴展目標[1-2]，這類跟蹤問題便稱為擴展目標跟蹤(EOT，Extended Object Tracking)。擴展目標具有不同空間分布的多個量測源，也稱作反射點，這些點會產生多個測量值。如何更好地對目標進行位置估計，需要建立當前目標和其測量值得關聯，當目標數較多時，這便成了一個高度復雜的問題。首先在量測建模方面，Gilholm等人[1]提出了非齊次泊松點過程(PPP)，將目標數目建模為服從泊松分布模型，多個量測點分布在目標周圍，這種模型具有數學上的方便，可以避免顯式求解。在隨機集理論(RFS)和PPP模型的基礎上，Mahler在貝葉斯濾波的框架下推導并提出了擴展目標概率假設密度濾波器(Extended-Target PHD，ET-PHD)[2]。Karl等人在此基礎上，將運動轉移模型假設是線性的，同時假設觀測噪聲服從高斯分布，從而可以得到算法的閉合解，便可在已有的卡爾曼濾波理論框架下求得濾波器的快速迭代方程，進一步發展了概率假設密度濾波器在擴展目標跟蹤領域的應用[3]。

隨著RFS理論在EOT問題上的引入，相關研究成果便層出不窮[4-6]。基于RFS的PHD方法被認為是實現EOT問題的一種有效技術手段[7-9]，然而現有方法大多是基于線性高斯模型的，而實際中大部分情況都是非線性非高斯的。雖然將粒子濾波方法引入，提出的SMCPHD濾波器能夠很好地處理非線性問題，但是計算量也是算法應用的一大瓶頸。近年來，有研究人員將區間分析技術和粒子濾波進行結合，提出了一種被稱為盒粒子濾波(Box Particle Filter，BPF)的算法。與傳統的粒子濾波采用誤差統計模型不同，盒粒子濾波采用盒粒子和誤差界限模型對量測點進行建模表示，經過這樣處理后可以大幅降低所需要的粒子數，對粒子濾波固有的運算復雜度較高的問題具有較好的改善作用。近幾年，很多研究者已經將區間分析技術用于跟蹤問題并取得了很好的效果[10-11]，先后提出基于盒粒子的單目標Bernoulli算法[12-14]、基于盒粒子的單擴展目標Bernoulli算法[15-17]以及基于盒粒子的多目標PHD濾波算法[18]等。上述方法雖采用了區間分析理論，但是依然處理的是點量測數據而實際復雜場景下我們得到的數據一般都包含有較大的測量誤差，采用區間量測進行表示可以更好地容納這種不確定性。

對此，本文提出了一種基于BPF的多擴展目標伯努利濾波算法(ET-BP-MeMBer)。在區間量測的假設前提下，改進了偽似然函數，并針對存在的區間量測集劃分問題，將相互距離度量用于近鄰傳播聚類算法，提出了基于MD-AP聚類的區間量測集劃分方法。

1 盒粒子濾波

考慮如下非線性系統模型：

xk+1=f(xk,ωk)

(1)

zk=h(xk,vk)

(2)

式中，xk為擴展目標的狀態，ωk表示過程噪聲，vk表示量測噪聲，f(·)為非線性狀態轉移函數，h(·)為量測方程，zk為擴展目標的觀測值。

對于如上的非線性跟蹤系統，廣泛采用粒子濾波算法進行求解。但是粒子濾波算法并不是十全十美的，粒子退化、計算量大等問題仍然制約著該算法的發展。近年來一種被稱為盒粒子濾波的方法得到了廣泛地研究。

盒粒子濾波算法采用占據一定空間且面積可控的矩形區域來代替傳統的點粒子去描述目標的狀態分布。基本的算法過程如圖1所示，簡述如下：

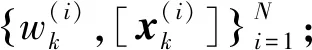
2)狀態預測：k+1刻目標的預測概率密度函數為：

(3)

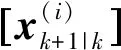
p(zk+1|xk+1)=U[zk+1](g(xk+1))

(4)

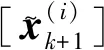
(5)

(6)

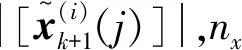
(7)

5)重采樣：為了保持盒粒子多樣性，必須進行重采樣，由于處理的是帶誤差的數據，傳統的適用于粒子濾波的重采樣算法無法適用，本文采用隨機子劃分進行處理。

由于觀測不確定性以及未知的各類偏差導致量測數據常常表現為區間的形式，如a=[a-,a+]。在這種條件下，傳統的算法難以適用，便迫切需要尋求合適的濾波算法。

2 本文算法

本章首先對擴展目標伯努利濾波算法的大致過程進行簡要介紹，接著詳細敘述本文所提算法的主要過程。

2.1 擴展目標MeMBer濾波

在線性高斯的條件下，文獻[13]對擴展目標MeMBer濾波算法進行了高斯混合實現。首先對傳統ET-MeMBer濾波算法的跟蹤過程簡述如下：

1)預測

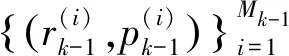
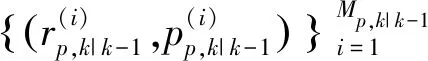
(8)

式(8)中，

(9)

(10)

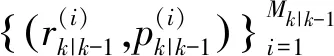
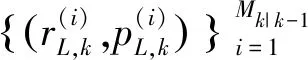
(11)

式(11)中，

(12)

(13)

(14)

(15)

2.2 基于盒粒子濾波的擴展目標MeMBer算法

上述2.1節給出了標準的ET-MeMBer濾波跟蹤算法，但是在實際應用中，各種復雜因素常常導致產生不確定性量測，上述算法便無法處理。除此之外，在利用粒子濾波實施該算法時，為保證濾波精度，需要大量的粒子來覆蓋目標的后驗概率密度，增加了算法的運算復雜度。針對上述問題，本文假設量測為區間的形式，將盒粒子濾波方法代替粒子濾波方法，提出了ET-BP-MeMBer濾波算法，具體算法步驟如下：

步驟1 預測

設k-1時刻的多擴展目標PDF可表示為：

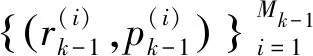
(16)

(17)

則預測PDF為：

8月28日，湖北省發改委已正式同意“東風汽車集團股份有限公司在武漢市建設乘用車擴建項目”，據了解，該項目將用于提升東風日產的在華產能，但是具體運營模式仍處在內部探討階段。新工廠位于武漢經濟技術開發區鳳凰工業園，分兩期建設，年產能30萬輛，能夠生產包括乘用車（含傳統燃油車和純電動車型）及其他類乘用車（含傳統燃油車和混合動力車型），建設期為2019年1月至2022年12月。該項目總投資為98.51億元，其中東風公司持有66.86%的股份。

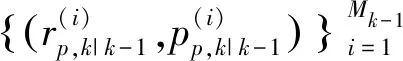
(18)

步驟2 更新

假設k時刻預測為：

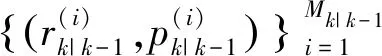
(19)

(20)

則更新的后驗密度為：

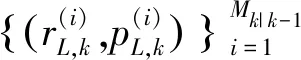
(21)

其中，

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

步驟3 約束傳播

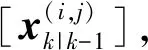
[x]=[x]×[xz]，[y]=[y]×[yz]

步驟4 重采樣

為了保證粒子的多樣性，以及區間粒子的特殊性，本文利用隨機子劃分的方法進行重采樣。

步驟5 修剪與合并

隨著迭代更新和目標數的增加，伯努利項數目將會越來越多，為了提高計算效率，同時避免虛假軌跡的干擾，需要對伯努利項進行刪減處理，一方面避免了干擾，另一方面也降低了計算量。

步驟6 狀態提取

僅提取概率大于0.5的伯努利分量，再利用傳統的Kmeans算法進行聚類，從而獲得目標的狀態估計，即：

(31)

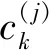
2.3 基于MD-AP的區間量測劃分

AP算法是一種被廣泛使用的聚類方法[19]。在區間量測的環境下，所有的數和矢量均以區間的形式給出，傳統的度量方法難以適用，為此，采用一種新的度量方法稱之為相互度量。

設a=[a-，a+]、b=[b-，b+]為兩個區間量測，則將a相對于b的相互距離：

(32)

而b相對于a的相互距離：

(33)

式(33)中，(a∧b)=Max(a+,b+)-Min(a-,b-)。

由于a相對于b的相互距離并非總等于b相對于a的相互距離，為了適用于AP算法，本節定義a和b的相似性度量為：

(34)

設A=[a1,a2,…,an]、B=[b1,b2,…,bn]為兩個區間矢量，則A相對于B的區間相似度為：

(35)

接著直接采用前文提過的AP算法，算法中要求的相似度矩陣采用相互距離來計算，這樣便得到了適用于區間量測的劃分算法，如下所示：

步驟1 采用相互距離構建所有量測點間的相似度矩陣，將代表矩陣和適選矩陣的元素都初始化為0：a(0)(i,k)=r(0)(i,k)=0；

步驟2 對建立的兩個矩陣進行交替更新，當滿足收斂條件時停止迭代，并通過對各個量測點進行計算尋找各自的中心點從而實現量測集劃分；

至此，給出了基于MD-AP的區間量測劃分主要步驟。與傳統點量測集劃分相比，區間量測集劃分主要在于對區間量測點相似度的定義以及準則函數的確定上有所不同。

3 算法分析及仿真實驗

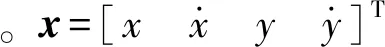
表1 目標初始狀態和運動信息Tab.1 Target initial states and moving information

其狀態轉移密度為：

πk|k+1(x|x′)=N(x;Fx′,Q)

(36)

式(36)中，

Q=diag(0.01×I9，Qk)，Qk=diag(Q1,Q1)，

其中，I9表示9維的單位對角陣，T表示采樣周期。

圓形目標半徑R=20 m，則目標狀態可表示為：

(37)

量測方程h(x)定義為：

(38)

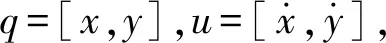
圖1給出了多擴展目標一次MC仿真的態勢圖，其中圓形表示目標，方塊表示雜波和量測。圖2給出了跟蹤過程中目標數目的估計比較。可以看出，本文算法在對目標進行數據估計時波動更小，估計更穩定。

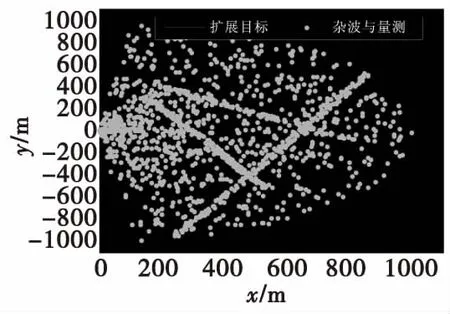
圖1 態勢圖Fig.1 The situation of targets

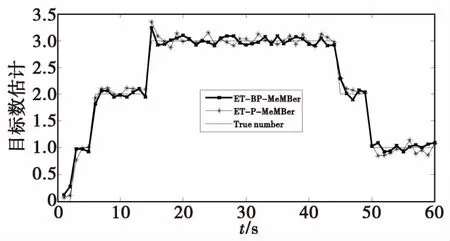
圖2 目標個數估計圖Fig.2 The estimated number of targets

為了對兩種算法的跟蹤性能表現情況進行充分比較，對算法進行了多次MCMC仿真實驗，如圖3-圖6所示。

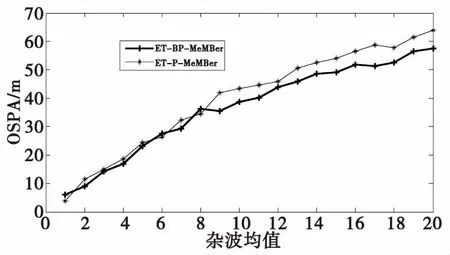
圖3 平均OSPA距離與雜波的關系Fig.3 The relationship between the mean OSPA distance and mean number of clutters

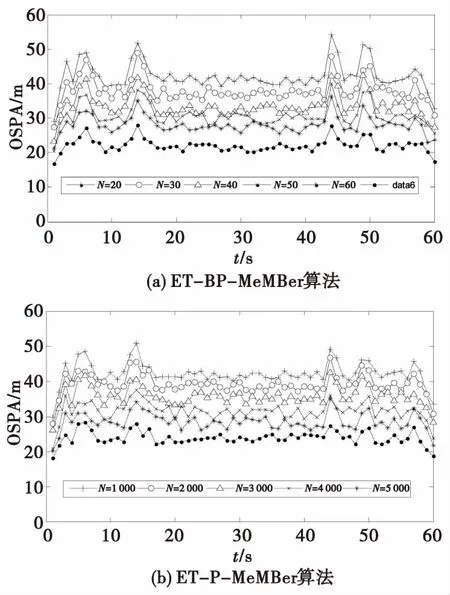
圖4 兩種算法OSPA距離與粒子數關系Fig.4 The relationship between OSPA distance and number of particles

圖3表示算法平均OSPA距離隨雜波的變化情況。從圖中可以很明顯地看出雜波對算法的性能有較大的影響，本文算法稍優于原始算法。但是值得注意的是，兩種算法均不能達到對雜波的良好抑制作用。

圖4對兩種算法在不同粒子數下的平均OSPA進行了比較試驗，其中圖4(a)為本文所提算法，N表示設置的粒子數目。隨著粒子數的增加，兩種算法濾波的OSPA值都有逐步減少的趨勢。但是可以看出，在近似的性能表現要求下，本文算法所需要的粒子數目遠遠小于基于點粒子濾波的方法。

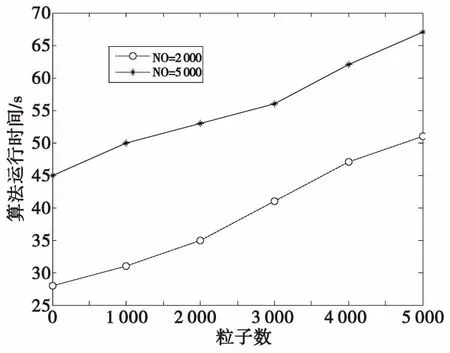
圖5 ET-P-MeMber算法平均運行時間Fig.5 The average operation time of ET-P-MeMBer

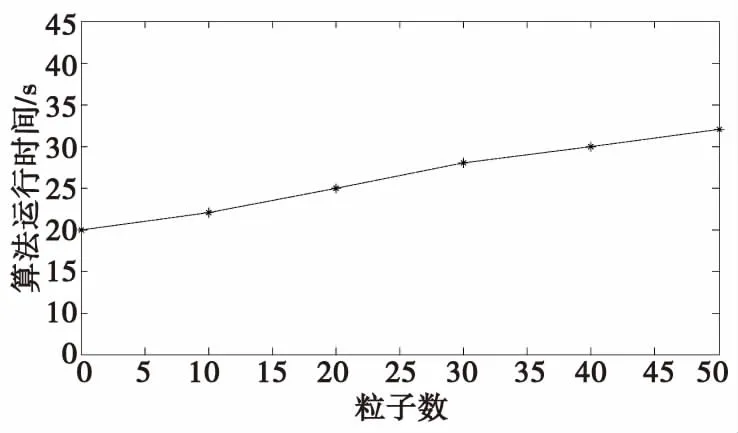
圖6 ET-BP-MeMber算法平均運行時間Fig.6 Theaverage operation time of ET-BP-MeMBer

圖5對算法的運行時間進行對比，主要通過在相同新生目標數的前提下，各自產生不同新生粒子數的情況。為了捕獲新生目標，ET-P-MeMBer算法需要產生大量的新生粒子，使得運算量有所增加，而ET-BP-MeMBer算法的主要時間消耗在盒粒子濾波的區間運算上。綜合來看，本文提出的ET-BP-MeMBer算法由于在運算效率和精度上有著良好的折中，使得可以更好地應用于實際場景中。

4 結論

針對不確定量測下的對擴展目標跟蹤問題，本文提出了基于MD-AP的ET-BP-MeMBer算法。當量測采用區間表示的時候，傳統的處理手段難以利用，本文將盒粒子濾波算法用于濾波求解過程，在建模了量測誤差的前提下，較大地提升了算法的運算效率，同時本文提出了基于相互距離的AP算法用于處理區間量測集劃分問題。實驗結果表明本文算法有著較好的跟蹤精度和計算效率。