基于前置反饋補償?shù)幕鸺袕椊怦罘椒?/h1>
2019-05-15 06:55:24魏志芳曹紅松
探測與控制學(xué)報 2019年2期
劉 偉,魏志芳,曹紅松
(1.中北大學(xué)機電工程學(xué)院,山西 太原,030051;2.重慶航天機電設(shè)計院,重慶 400039)
0 引言
由于旋轉(zhuǎn)火箭靶彈在飛行過程中以一定的滾轉(zhuǎn)角速度旋轉(zhuǎn),它獨特的動態(tài)特性使其控制方法具有一定的特殊性,導(dǎo)致不能直接應(yīng)用非旋轉(zhuǎn)式戰(zhàn)術(shù)導(dǎo)彈的現(xiàn)有研究成果,在技術(shù)層面提出了一些新的問題。火箭靶彈在飛行過程中以一定的滾轉(zhuǎn)角速度旋轉(zhuǎn),其動態(tài)特性的獨特性主要體現(xiàn)在俯仰和偏航通道之間的強耦合上,這些強耦合的主要原因包括Magnus效應(yīng)引起的氣動交聯(lián),陀螺效應(yīng)引起的慣性交聯(lián)以及運動學(xué)延遲誘導(dǎo)的控制交聯(lián)。由于這些交聯(lián)因素,旋轉(zhuǎn)靶彈的運動學(xué)與控制模型可視為一個存在俯仰和偏航通道強耦合的雙輸入-雙輸出的動態(tài)系統(tǒng)[1]。針對雙通道多輸入多輸出、強耦合、參數(shù)時變的特點,需要對靶彈的耦合特性和相應(yīng)的解耦控制方法進行分析。
目前工程中經(jīng)常使用基于插值的增益調(diào)度輔助解耦,由于需要預(yù)先計算大量的特征點,當(dāng)特征點較少并且滾動導(dǎo)彈氣動非線性較強時,基于插值法計算的反饋增益精度不高[2-4]。而一些非線性解耦算法,如動態(tài)逆解耦算法和H∞魯棒變增益算法,需要的模型精度高,計算量大,比線性解耦算法更為復(fù)雜[5]。為了簡化工程計算量,實現(xiàn)耦合矩陣的快速求解,本文提出了利用對角優(yōu)勢化特性設(shè)計動態(tài)預(yù)補償矩陣的前置反饋補償解耦方法。
1 前置反饋補償技術(shù)
前置反饋補償技術(shù)是采用一種動態(tài)預(yù)補償矩陣來實現(xiàn)解耦的一種技術(shù)。通過引入一個預(yù)補償器KP,使得KP·GP(s)是對角占優(yōu)的,便可以將補償后的俯仰、偏航通道進行單獨設(shè)計,而不必考慮彼此的耦合作用[6]。前置反饋補償解耦原理如圖1所示。
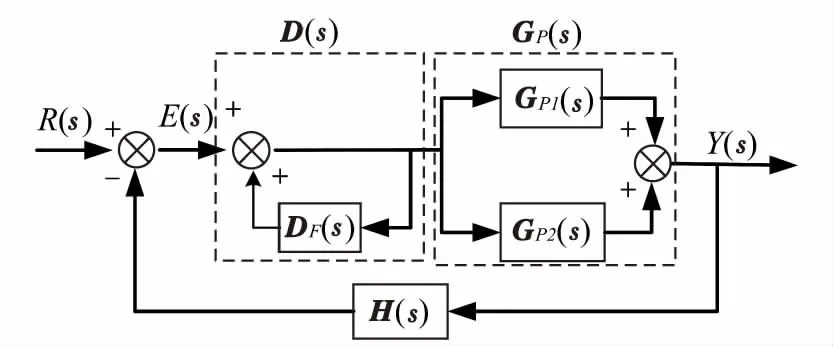
圖1 旋轉(zhuǎn)靶彈前置反饋補償解耦原理圖Fig.1 Decoupling principle diagram of pre-feedback compensation for target missile
圖1中,R(s),E(s),Y(s)分別表示輸入信號、偏差信號和輸出信號、H(s)為反饋通道傳遞函數(shù)矩陣,GP(s)由代表主對角線元素矩陣的GP1(s)和代表非對角線元素矩陣的GP2(s)組成,表示耦合對象傳遞函數(shù)矩陣,D(s)表示引入的“預(yù)補償器”矩陣。其完全解耦的補償矩陣DF(s)為:
(1)
2 火箭靶彈解耦方法
火箭靶彈解耦方法是在靶彈運動學(xué)和控制頻域模型基礎(chǔ)上,將開環(huán)傳遞函數(shù)矩陣分解為動力學(xué)耦合和控制耦合,基于前置反饋補償技術(shù)將補償后的俯仰、偏航通道進行單獨設(shè)計,進而實現(xiàn)靶彈姿態(tài)和過載解耦控制系統(tǒng)的設(shè)計。
2.1 運動學(xué)耦合特性分析

(2)
2.2 控制耦合特性分析
由文獻[9]可知:
(3)
式(3)中,W(s)為控制耦合傳遞函數(shù)矩陣,W12和W21項表示由靶彈主體的旋轉(zhuǎn)和轉(zhuǎn)向裝置延遲引起的交叉耦合,ωx為靶彈的滾轉(zhuǎn)角速度,τ為舵機的一階慣性常數(shù)。當(dāng)ωx=0,W12=W21=0表明方向舵系統(tǒng)僅具有輸入輸出轉(zhuǎn)換關(guān)系,沒有耦合。當(dāng)ωx≠0時,俯仰和偏航通道之間產(chǎn)生控制交叉作用,產(chǎn)生控制耦合。
2.3 火箭靶彈姿態(tài)解耦
2.3.1 控制耦合W(s)的解耦
由式(1),式(2)得到W(s)的前置反饋補償矩陣為:
(4)
2.3.2 運動學(xué)耦合G(s)的解耦
由于補償解耦矩陣為前置反饋補償矩陣,并設(shè)立在舵伺服系統(tǒng)之前,因此不能忽略控制耦合傳遞函數(shù)矩陣W(s)對反饋量的影響,因此由式(1),式(2),式(3)得到運動學(xué)耦合G(s)的前置反饋補償解耦矩陣為:
(5)
結(jié)合式(1)—式(5)用結(jié)構(gòu)圖的方式表示俯仰和偏航通道姿態(tài)控制系統(tǒng)的前置反饋解耦,如圖2所示。

圖2 姿態(tài)控制系統(tǒng)解耦結(jié)構(gòu)圖Fig.2 Decoupling structure diagram of attitude control system
2.4 火箭靶彈過載解耦
2.4.1 過載回路傳遞函數(shù)
由文獻[7]可知,前向通道傳遞函數(shù)矩陣Gd為:
(6)
反饋通道傳遞函數(shù)Hd為:
(7)
閉環(huán)傳遞函數(shù)Ωd為:
(8)
式中,CS表示由于靶彈姿態(tài)運動而引起的加速度,ka表示反饋回路增益,kg表示阻尼回路增益。
2.4.2 過載回路解耦矩陣
由式(1),式(8)得到過載回路前置反饋補償解耦矩陣DFG′為:
(9)
旋轉(zhuǎn)靶彈過載回路前置反饋補償解耦的基本結(jié)構(gòu)如圖3所示。

圖3 過載回路前置反饋補償解耦結(jié)構(gòu)圖Fig.3 Pre-feedback compensation decoupling structure diagram of overload circuit
由于反饋補償解耦矩陣DFG′含有速率陀螺和加速度計的反饋信息,因此,欲實現(xiàn)系統(tǒng)的完全解耦,需要得到ka,kg,C。
2.4.3 過載解耦控制系統(tǒng)參數(shù)設(shè)計
1)加速度計相對質(zhì)心位置C。本文假設(shè)加速度計于質(zhì)心位置重合,故取值為0。
2)反饋回路增益ka。考慮到靶彈的角運動微分量反饋和阻尼回路增益kg對自動駕駛儀增益的貢獻,初步將反饋回路增益ka定為0.8。
3)阻尼回路增益kg。以俯仰通道為例,過載自動駕駛儀的基本結(jié)構(gòu)如圖4所示。
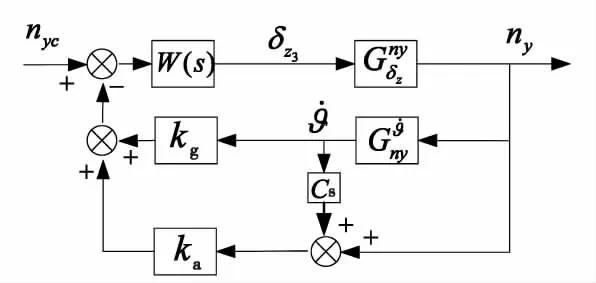
圖4 過載自動駕駛儀的基本結(jié)構(gòu)Fig.4 Basic structure of overloaded autopilot
得到模型的高階傳遞函數(shù)簡化為:
(10)
用比例增益kS代替舵機環(huán)節(jié)W(s),得到過載指令nyc到實際過載ny的閉環(huán)傳遞函數(shù)為:
(11)
式(11)中,
其中,V表示靶彈的速度,g表示靶彈的重力加速度,ξN表示自動駕駛儀控制回路在阻尼系數(shù),TN,KN表示系統(tǒng)增益,a22,a24,…,a35稱為動力系數(shù),它表征靶彈的運動學(xué)特征,其具體物理學(xué)意義可由文獻[7]給出。
由文獻[10]得知:在ξN=0.5,KN=10時,系統(tǒng)在調(diào)節(jié)時間、響應(yīng)速度以及超調(diào)量等方面較優(yōu)。將特征點1的動力系數(shù)以及其他相關(guān)參數(shù)代入,可得,ks=0.11,kg=13.3。
3 仿真驗證
3.1 姿態(tài)解耦控制性能仿真驗證

1)解耦前姿態(tài)控制系統(tǒng)的俯仰和偏航通道階躍輸入的耦合響應(yīng)分別如圖5和圖6所示。
從圖5和圖6的仿真曲線可以看出系統(tǒng)在未解耦前,偏航和俯仰通道存在明顯的耦合響應(yīng)。正向的俯仰引起正向的偏航以及正向的偏航引起負(fù)向的俯仰,而俯仰和偏航引起的交連部分的影響是使其自身不斷減小,故滾轉(zhuǎn)靶彈在無控飛行狀態(tài)下,彈體姿態(tài)角運動是呈滾轉(zhuǎn)穩(wěn)定的。由于階躍輸入中的δz_r、δy_r表示周期平均控制力的最大輸入,因此即使靶彈是旋轉(zhuǎn)穩(wěn)定的,在俯仰和偏航通道的輸出響應(yīng)仍會有震蕩并呈向上增加的趨勢。
2)解耦后姿態(tài)控制系統(tǒng)的俯仰和偏航通道階躍輸入的耦合響應(yīng)分別如圖7和圖8所示。
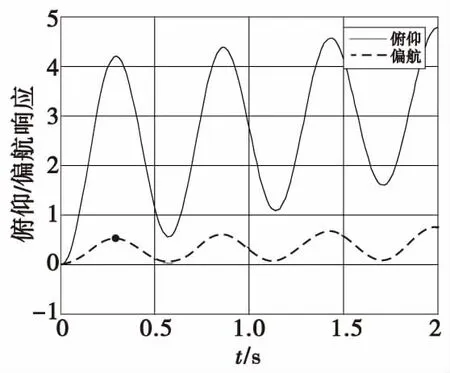
圖5 解耦前俯仰通道階躍輸入耦合響應(yīng)Fig.5 Coupling response of pitch channel step input before decoupling
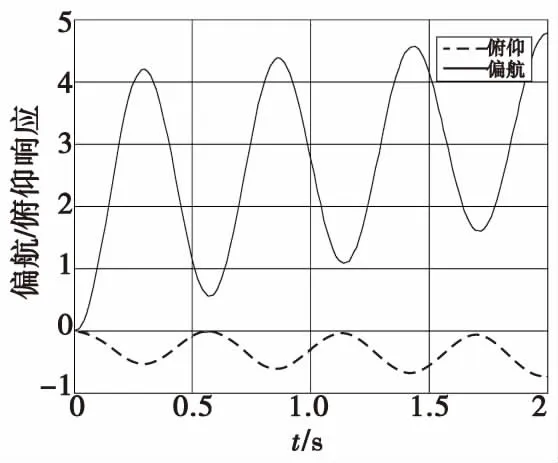
圖6 解耦前偏航通道階躍輸入耦合響應(yīng)Fig.6 Coupling response of yaw channel step input before decoupling
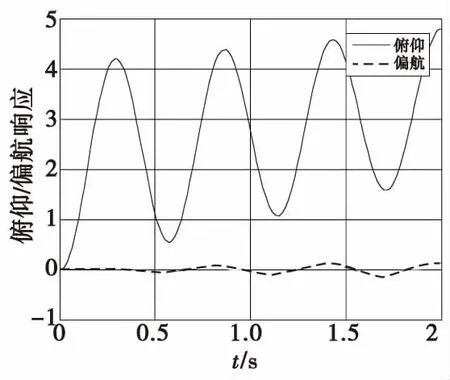
圖7 解耦后俯仰通道階躍輸入響應(yīng)Fig.7 Response of decoupled pitch channel step input
通過圖7,圖8可以得出,采用前置反饋補償解耦的方法有效的改善了系統(tǒng)的俯仰-偏航響應(yīng),并實現(xiàn)了系統(tǒng)的近似解耦。
3.2 過載解耦控制性能仿真驗證
以俯仰通道為例,前置反饋補償解耦前后,俯仰階躍輸入的俯仰、偏航通道響應(yīng)分別如圖9和圖10所示。
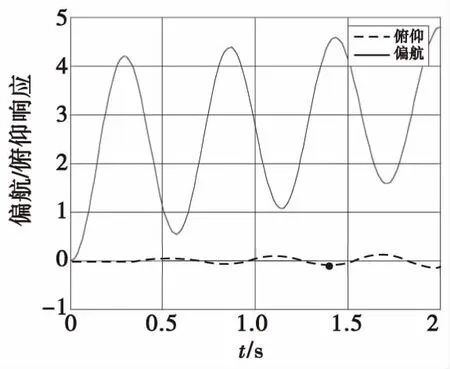
圖8 解耦后偏航通道階躍輸入響應(yīng)Fig.8 Response of decoupled yaw channel step input

圖9 解耦前俯仰階躍輸入響應(yīng)Fig.9 Response of pitch channel step input before decoupling
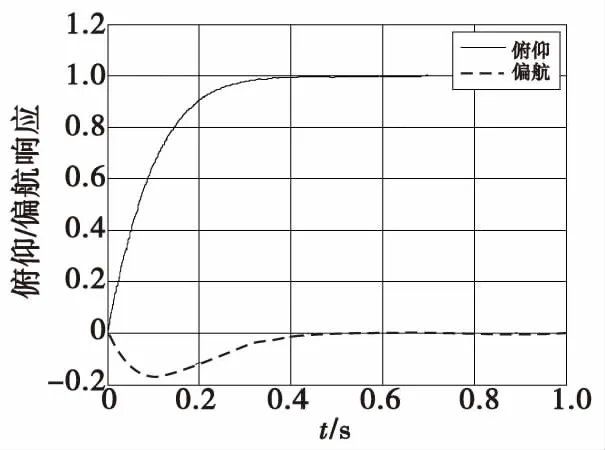
圖10 解耦后俯仰階躍輸入響應(yīng)Fig.10 Response of decoupled pitch step input
從圖9中我們可以得出系統(tǒng)在解耦前,俯仰和偏航通道均受到耦合的作用。其中,耦合使得俯仰通道在穩(wěn)態(tài)值增加了近4%,而俯仰通道的階躍輸入導(dǎo)致偏航通道產(chǎn)生負(fù)的交叉響應(yīng),使偏航通道引起的最大交叉響應(yīng)為-0.4,穩(wěn)態(tài)響應(yīng)為-0.18。在前置反饋補償解耦后,有效的消除了耦合對俯仰通道的影響,并且使偏航通道引起的最大交叉響應(yīng)為-0.17左右,穩(wěn)態(tài)響應(yīng)為0,解耦效果良好。
4 結(jié)論
本文提出了基于前置反饋補償?shù)幕鸺袕椊怦罘椒āT摲椒ㄔ诎袕椷\動學(xué)和控制頻域模型基礎(chǔ)上,將開環(huán)傳遞函數(shù)矩陣分解為運動學(xué)耦合和控制耦合,通過引入一個預(yù)補償器,使得運動/控制耦合的傳遞函數(shù)矩陣是對角占優(yōu)的,便可以將補償后的俯仰、偏航通道進行單獨設(shè)計,進而實現(xiàn)靶彈姿態(tài)和過載解耦控制系統(tǒng)的設(shè)計。仿真結(jié)果表明,采用前置反饋補償解耦方法有效地解決了旋轉(zhuǎn)靶彈俯仰和偏航通道之間的耦合效應(yīng),并且具有解耦器結(jié)構(gòu)簡單,動態(tài)響應(yīng)性能好等優(yōu)點,在工程上具有一定的指導(dǎo)意義。
劉 偉,魏志芳,曹紅松
(1.中北大學(xué)機電工程學(xué)院,山西 太原,030051;2.重慶航天機電設(shè)計院,重慶 400039)
0 引言
由于旋轉(zhuǎn)火箭靶彈在飛行過程中以一定的滾轉(zhuǎn)角速度旋轉(zhuǎn),它獨特的動態(tài)特性使其控制方法具有一定的特殊性,導(dǎo)致不能直接應(yīng)用非旋轉(zhuǎn)式戰(zhàn)術(shù)導(dǎo)彈的現(xiàn)有研究成果,在技術(shù)層面提出了一些新的問題。火箭靶彈在飛行過程中以一定的滾轉(zhuǎn)角速度旋轉(zhuǎn),其動態(tài)特性的獨特性主要體現(xiàn)在俯仰和偏航通道之間的強耦合上,這些強耦合的主要原因包括Magnus效應(yīng)引起的氣動交聯(lián),陀螺效應(yīng)引起的慣性交聯(lián)以及運動學(xué)延遲誘導(dǎo)的控制交聯(lián)。由于這些交聯(lián)因素,旋轉(zhuǎn)靶彈的運動學(xué)與控制模型可視為一個存在俯仰和偏航通道強耦合的雙輸入-雙輸出的動態(tài)系統(tǒng)[1]。針對雙通道多輸入多輸出、強耦合、參數(shù)時變的特點,需要對靶彈的耦合特性和相應(yīng)的解耦控制方法進行分析。
目前工程中經(jīng)常使用基于插值的增益調(diào)度輔助解耦,由于需要預(yù)先計算大量的特征點,當(dāng)特征點較少并且滾動導(dǎo)彈氣動非線性較強時,基于插值法計算的反饋增益精度不高[2-4]。而一些非線性解耦算法,如動態(tài)逆解耦算法和H∞魯棒變增益算法,需要的模型精度高,計算量大,比線性解耦算法更為復(fù)雜[5]。為了簡化工程計算量,實現(xiàn)耦合矩陣的快速求解,本文提出了利用對角優(yōu)勢化特性設(shè)計動態(tài)預(yù)補償矩陣的前置反饋補償解耦方法。
1 前置反饋補償技術(shù)
前置反饋補償技術(shù)是采用一種動態(tài)預(yù)補償矩陣來實現(xiàn)解耦的一種技術(shù)。通過引入一個預(yù)補償器KP,使得KP·GP(s)是對角占優(yōu)的,便可以將補償后的俯仰、偏航通道進行單獨設(shè)計,而不必考慮彼此的耦合作用[6]。前置反饋補償解耦原理如圖1所示。

圖1 旋轉(zhuǎn)靶彈前置反饋補償解耦原理圖Fig.1 Decoupling principle diagram of pre-feedback compensation for target missile
圖1中,R(s),E(s),Y(s)分別表示輸入信號、偏差信號和輸出信號、H(s)為反饋通道傳遞函數(shù)矩陣,GP(s)由代表主對角線元素矩陣的GP1(s)和代表非對角線元素矩陣的GP2(s)組成,表示耦合對象傳遞函數(shù)矩陣,D(s)表示引入的“預(yù)補償器”矩陣。其完全解耦的補償矩陣DF(s)為:
(1)
2 火箭靶彈解耦方法
火箭靶彈解耦方法是在靶彈運動學(xué)和控制頻域模型基礎(chǔ)上,將開環(huán)傳遞函數(shù)矩陣分解為動力學(xué)耦合和控制耦合,基于前置反饋補償技術(shù)將補償后的俯仰、偏航通道進行單獨設(shè)計,進而實現(xiàn)靶彈姿態(tài)和過載解耦控制系統(tǒng)的設(shè)計。
2.1 運動學(xué)耦合特性分析

(2)
2.2 控制耦合特性分析
由文獻[9]可知:
(3)
式(3)中,W(s)為控制耦合傳遞函數(shù)矩陣,W12和W21項表示由靶彈主體的旋轉(zhuǎn)和轉(zhuǎn)向裝置延遲引起的交叉耦合,ωx為靶彈的滾轉(zhuǎn)角速度,τ為舵機的一階慣性常數(shù)。當(dāng)ωx=0,W12=W21=0表明方向舵系統(tǒng)僅具有輸入輸出轉(zhuǎn)換關(guān)系,沒有耦合。當(dāng)ωx≠0時,俯仰和偏航通道之間產(chǎn)生控制交叉作用,產(chǎn)生控制耦合。
2.3 火箭靶彈姿態(tài)解耦
2.3.1 控制耦合W(s)的解耦
由式(1),式(2)得到W(s)的前置反饋補償矩陣為:
(4)
2.3.2 運動學(xué)耦合G(s)的解耦
由于補償解耦矩陣為前置反饋補償矩陣,并設(shè)立在舵伺服系統(tǒng)之前,因此不能忽略控制耦合傳遞函數(shù)矩陣W(s)對反饋量的影響,因此由式(1),式(2),式(3)得到運動學(xué)耦合G(s)的前置反饋補償解耦矩陣為:
(5)
結(jié)合式(1)—式(5)用結(jié)構(gòu)圖的方式表示俯仰和偏航通道姿態(tài)控制系統(tǒng)的前置反饋解耦,如圖2所示。

圖2 姿態(tài)控制系統(tǒng)解耦結(jié)構(gòu)圖Fig.2 Decoupling structure diagram of attitude control system
2.4 火箭靶彈過載解耦
2.4.1 過載回路傳遞函數(shù)
由文獻[7]可知,前向通道傳遞函數(shù)矩陣Gd為:
(6)
反饋通道傳遞函數(shù)Hd為:
(7)
閉環(huán)傳遞函數(shù)Ωd為:
(8)
式中,CS表示由于靶彈姿態(tài)運動而引起的加速度,ka表示反饋回路增益,kg表示阻尼回路增益。
2.4.2 過載回路解耦矩陣
由式(1),式(8)得到過載回路前置反饋補償解耦矩陣DFG′為:
(9)
旋轉(zhuǎn)靶彈過載回路前置反饋補償解耦的基本結(jié)構(gòu)如圖3所示。

圖3 過載回路前置反饋補償解耦結(jié)構(gòu)圖Fig.3 Pre-feedback compensation decoupling structure diagram of overload circuit
由于反饋補償解耦矩陣DFG′含有速率陀螺和加速度計的反饋信息,因此,欲實現(xiàn)系統(tǒng)的完全解耦,需要得到ka,kg,C。
2.4.3 過載解耦控制系統(tǒng)參數(shù)設(shè)計
1)加速度計相對質(zhì)心位置C。本文假設(shè)加速度計于質(zhì)心位置重合,故取值為0。
2)反饋回路增益ka。考慮到靶彈的角運動微分量反饋和阻尼回路增益kg對自動駕駛儀增益的貢獻,初步將反饋回路增益ka定為0.8。
3)阻尼回路增益kg。以俯仰通道為例,過載自動駕駛儀的基本結(jié)構(gòu)如圖4所示。

圖4 過載自動駕駛儀的基本結(jié)構(gòu)Fig.4 Basic structure of overloaded autopilot
得到模型的高階傳遞函數(shù)簡化為:
(10)
用比例增益kS代替舵機環(huán)節(jié)W(s),得到過載指令nyc到實際過載ny的閉環(huán)傳遞函數(shù)為:
(11)
式(11)中,
其中,V表示靶彈的速度,g表示靶彈的重力加速度,ξN表示自動駕駛儀控制回路在阻尼系數(shù),TN,KN表示系統(tǒng)增益,a22,a24,…,a35稱為動力系數(shù),它表征靶彈的運動學(xué)特征,其具體物理學(xué)意義可由文獻[7]給出。
由文獻[10]得知:在ξN=0.5,KN=10時,系統(tǒng)在調(diào)節(jié)時間、響應(yīng)速度以及超調(diào)量等方面較優(yōu)。將特征點1的動力系數(shù)以及其他相關(guān)參數(shù)代入,可得,ks=0.11,kg=13.3。
3 仿真驗證
3.1 姿態(tài)解耦控制性能仿真驗證

1)解耦前姿態(tài)控制系統(tǒng)的俯仰和偏航通道階躍輸入的耦合響應(yīng)分別如圖5和圖6所示。
從圖5和圖6的仿真曲線可以看出系統(tǒng)在未解耦前,偏航和俯仰通道存在明顯的耦合響應(yīng)。正向的俯仰引起正向的偏航以及正向的偏航引起負(fù)向的俯仰,而俯仰和偏航引起的交連部分的影響是使其自身不斷減小,故滾轉(zhuǎn)靶彈在無控飛行狀態(tài)下,彈體姿態(tài)角運動是呈滾轉(zhuǎn)穩(wěn)定的。由于階躍輸入中的δz_r、δy_r表示周期平均控制力的最大輸入,因此即使靶彈是旋轉(zhuǎn)穩(wěn)定的,在俯仰和偏航通道的輸出響應(yīng)仍會有震蕩并呈向上增加的趨勢。
2)解耦后姿態(tài)控制系統(tǒng)的俯仰和偏航通道階躍輸入的耦合響應(yīng)分別如圖7和圖8所示。

圖5 解耦前俯仰通道階躍輸入耦合響應(yīng)Fig.5 Coupling response of pitch channel step input before decoupling

圖6 解耦前偏航通道階躍輸入耦合響應(yīng)Fig.6 Coupling response of yaw channel step input before decoupling

圖7 解耦后俯仰通道階躍輸入響應(yīng)Fig.7 Response of decoupled pitch channel step input
通過圖7,圖8可以得出,采用前置反饋補償解耦的方法有效的改善了系統(tǒng)的俯仰-偏航響應(yīng),并實現(xiàn)了系統(tǒng)的近似解耦。
3.2 過載解耦控制性能仿真驗證
以俯仰通道為例,前置反饋補償解耦前后,俯仰階躍輸入的俯仰、偏航通道響應(yīng)分別如圖9和圖10所示。

圖8 解耦后偏航通道階躍輸入響應(yīng)Fig.8 Response of decoupled yaw channel step input

圖9 解耦前俯仰階躍輸入響應(yīng)Fig.9 Response of pitch channel step input before decoupling

圖10 解耦后俯仰階躍輸入響應(yīng)Fig.10 Response of decoupled pitch step input
從圖9中我們可以得出系統(tǒng)在解耦前,俯仰和偏航通道均受到耦合的作用。其中,耦合使得俯仰通道在穩(wěn)態(tài)值增加了近4%,而俯仰通道的階躍輸入導(dǎo)致偏航通道產(chǎn)生負(fù)的交叉響應(yīng),使偏航通道引起的最大交叉響應(yīng)為-0.4,穩(wěn)態(tài)響應(yīng)為-0.18。在前置反饋補償解耦后,有效的消除了耦合對俯仰通道的影響,并且使偏航通道引起的最大交叉響應(yīng)為-0.17左右,穩(wěn)態(tài)響應(yīng)為0,解耦效果良好。
4 結(jié)論
本文提出了基于前置反饋補償?shù)幕鸺袕椊怦罘椒āT摲椒ㄔ诎袕椷\動學(xué)和控制頻域模型基礎(chǔ)上,將開環(huán)傳遞函數(shù)矩陣分解為運動學(xué)耦合和控制耦合,通過引入一個預(yù)補償器,使得運動/控制耦合的傳遞函數(shù)矩陣是對角占優(yōu)的,便可以將補償后的俯仰、偏航通道進行單獨設(shè)計,進而實現(xiàn)靶彈姿態(tài)和過載解耦控制系統(tǒng)的設(shè)計。仿真結(jié)果表明,采用前置反饋補償解耦方法有效地解決了旋轉(zhuǎn)靶彈俯仰和偏航通道之間的耦合效應(yīng),并且具有解耦器結(jié)構(gòu)簡單,動態(tài)響應(yīng)性能好等優(yōu)點,在工程上具有一定的指導(dǎo)意義。

