壓電引信大著角發火性數值仿真方法

周 浪，王雨時，聞 泉，王光宇，張志彪

(南京理工大學機械工程學院，江蘇 南京 210094)

0 引言

壓電引信是現代彈藥中廣泛使用的觸發式引信之一，其特點是具有極高的瞬發度，能夠減少彈藥因著速不同造成的炸高散布[1]。為了確保壓電引信在實戰時能夠可靠作用，研制時需要對其作用可靠性進行考核。對于壓電引信工作性能的考核，傳統的方法是采用靶場試驗的方法，但是該方法需要消耗大量的人力和財力，并且難以深入分析試驗過程出現的故障原因和引信的具體失效過程。對于壓電引信的研究，現有文獻都是基于理論和試驗兩方面，通過數值仿真手段對其進行研究的文獻較少，僅有文獻[2]應用Autodyn仿真軟件對某空氣炮彈碰目標過程進行模擬，再現了其彈頭受力、變形過程，獲得了彈頭中壓力、應力、速度等各種力學參數的分布和時程圖，從而間接獲知壓電陶瓷輸出電能性能，但未從彈頭結構差異方面對彈頭中壓力、應力、速度等各種力學參數的影響進行深入研究。文獻[3]根據應力波的基本理論近似地分析計算了彈丸碰擊鋼甲時，頭部碰擊式壓電引信壓電機構中應力波的傳播過程，得出了不同結構中壓電陶瓷軸向應力的近似值，在計算過程中將引信頭部結構簡化成平頭，與實際引信頭結構差別較大，計算結果精度不高。文獻[4]以壓電引信電-1和電-2為例，討論了壓電引信發火和瞬發度的影響因素，并以大量的試驗數據為支撐，得出影響壓電引信瞬發度的因素主要包括彈速、目標、著角、彈頭部即引信頭部結構等，同時得出壓電晶體老化不會影響引信發火可靠性，但是對電雷管的起爆時間會產生1～2 μs的延遲。文獻[5]經推導壓電陶瓷壓電方程，得出影響壓電陶瓷壓電效應的應力包括三種正應力和兩種剪應力，其中與壓電陶瓷壓電效應直接相關的應力是與壓電晶體極化方向一致的正應力。文獻[6]對裝有壓電引信的低速破甲彈破甲不穩定的問題進行研究，分析得出影響破甲彈破甲不穩定的主要原因是目標(或靶板)接地電阻不同，降低了壓電引信瞬發度。本文針對試驗過程中壓電引信大著角對靶射擊試驗過程中瞎火原因難以分析的問題，采用ANSYS/LS-DYNA仿真軟件對引信頭采用不同結構和不同材料以不同著角碰擊均質鋼靶板時引信頭部變形對壓電晶體所產生的應力進行數值模擬，得出不同引信結構以及同種結構不同引信頭材料以不同著角碰擊均質鋼板時壓電晶體上的應力變化規律，藉此對引信頭部結構和參數設計進行優化，從而為提高引信大著角發火正確性探討可行途徑。

1 碰擊式壓電機構結構形式和壓電陶瓷壓電方程

根據配用彈種的不同，為了解決大著角發火與低靈敏度的矛盾，碰擊式壓電機構有各種不同的結構形式[5]。其中較為典型的碰擊式壓電機構包括帶環形槽的壓電機構、帶半球形壓電塊和防潮帽的壓電機構、整體塑封的壓電機構、帶碰擊開關的壓電機構、帶介質的壓電機構、帶球殼形陶瓷的壓電機構、用火帽沖力壓電的壓電機構和壓電陶瓷配置在彈體圓柱部的壓電機構8種[5]。某單兵火箭彈采用的碰擊式壓電機構屬于帶環形槽的壓電機構，其結構如圖1所示。

該壓電機構在引信頭上車制有環形槽，形成厚度為h的薄弱環節，以調節引信頭變形的難易程度[5]。陶瓷盒與引信頭之間有一間隙e，引信頭的軸向變形大于e時，才能向陶瓷施壓。在大著角時為了避免壓電陶瓷側壁局部受力使其提前破碎，陶瓷盒側面與引信頭之間也留有適當的徑向間隙，此徑向間隙一般為2 mm左右[5]。也可以在陶瓷盒里支承壓電陶瓷的陶瓷座上部做成錐孔(如圖1所示)，以保證有一定的徑向間隙，這樣對大著角發火也有利[5]。

在彈種、電雷管和壓電陶瓷參數確定以后，主要是通過改變引信頭薄弱部厚度h、間隙e、引信頭的材料和頂部形狀等來同時滿足大著角發火和低靈敏度的要求[5]。

對于壓電引信來說，壓電陶瓷性能和引信頭結構是決定引信發火正確性的關鍵。圖2為從壓電陶瓷中分離出來的單元立方體。圖3為壓電陶瓷受力和極化方向示意圖。

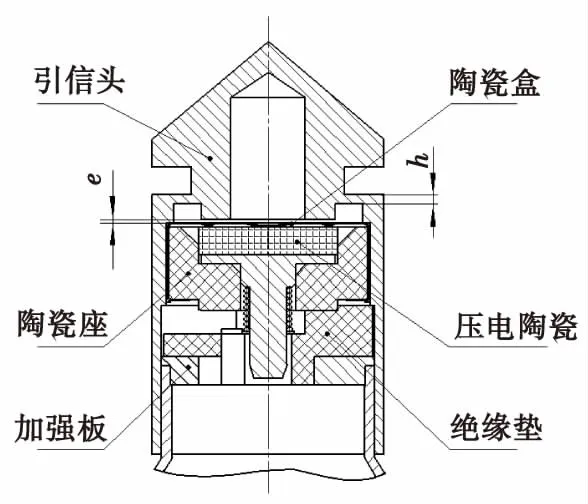
圖1 帶環形槽的引信壓電機構Fig.1 The piezoelectric structure with ring-shaped groove within fuze

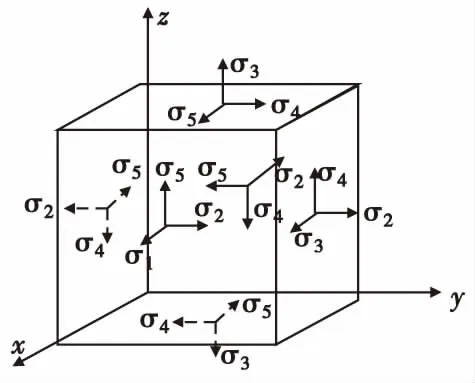
圖2 壓電陶瓷單元三維應力分布示意圖Fig.2 The scheme of three-dimensional stress

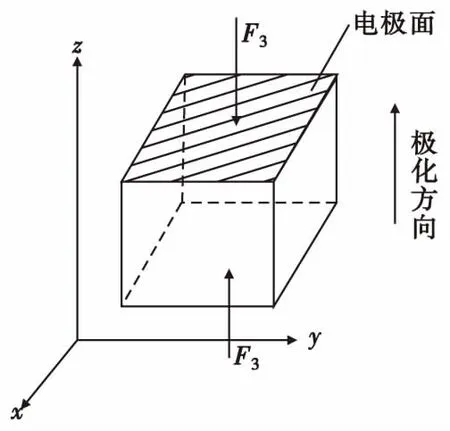
圖3 壓電陶瓷受力和極化方向示意圖Fig.3 The scheme of external force and polari-distribution onpiezoelectric ceramics element zation direction of piezoelectric ceramics

從圖2可看出，作用在壓電陶瓷立方體單元各個面上的應力共有六個，其中包括三個正應力σ1，σ2，σ3和三個剪應力σ4，σ5，σ6。從文獻[5]對壓電陶瓷壓電方程的推導可得出：在壓電陶瓷中，壓電效應與陶瓷中極化狀態的改變有關，而不是在任何力的作用下在任何方向都能產生壓電效應，只有在某些力的作用下在某些特定方向上才能產生壓電效應。具體地說，就是在正應力σ1，σ2，σ3的作用下，只有z方向，即原來的極化方向才有壓電效應；而在剪應力σ4，σ5的作用下，只在與極化方向垂直的方向上才有壓電效應[5]。

2 數值仿真方法

2.1 數值模擬研究思路

采用ANSYS/LS-DYNA軟件，對該單兵火箭彈以不同著角碰擊均質鋼靶板時引信頭部變形對壓電晶體作用過程進行數值仿真，得到不同結構、不同材料狀態下的引信頭以不同著角碰擊均質鋼靶板時引信壓電晶體表面法向最大應力峰值平均值和等效綜合最大應力峰值平均值。通過比較兩種應力峰值在不同碰擊著角情況下平均應力值，得出火箭彈以不同著角碰擊均質鋼靶板時壓電晶體表面應力的變化規律。由于不同引信結構、不同結構材料在碰擊過程中所產生的應力不同，傳到壓電晶體中的應力也就不同，所以對所測得的壓電晶體表面應力值進行對比，就可以對引信頭部結構進行優化并對最佳結構材料進行優選，使得引信頭部結構所產生的應力能夠更好地傳遞到壓電晶體上。

2.2 仿真模型建立

已知某單兵火箭彈參數：彈重2.25 kg；初速120±10 m/s，發動機工作后，在70 m處著靶速度295 m/s；彈丸最大直徑Dmax=80 mm；彈丸長度924.43～929.5 mm，飛行時彈丸長度920.57～929.5 mm；彈丸重心距彈底409 mm。

該火箭彈主要由引信彈頭壓電部分、藥柱、彈體、尾翼和引信彈底起爆部分組成。由于主要研究對象為引信彈頭壓電部分，所以為了三維建模和重心位置調整方便，把藥柱、彈體、尾翼和引信彈底起爆部分簡化成一個整體——彈體，而引信彈頭壓電部分則按產品具體結構簡化為引信頭、壓電陶瓷、陶瓷盒、絕緣座、絕緣墊、加強板、電極板，共七部分。仿真火箭彈垂直碰擊靶板過程簡化后的彈丸整體模型和引信彈頭壓電部分結構模型如圖4所示。

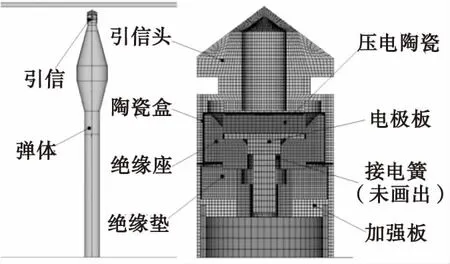
圖4 火箭彈垂直碰擊靶板三維簡化模型Fig.4 The simplified three-dimensional finite element model of rocket hitting target at verticality

為了簡化有限元模型，提高計算效率，作如下假設[2]：

1)對引信零件做簡化處理，保留其外形特征，去掉倒角。絕緣墊簡化為一形狀規則的階梯形空心柱體；

2)對簡化后的整體彈丸模型進行配重處理，使其與實體質量一致；

3)彈丸和靶板均為連續介質；

4)彈丸碰擊靶板的過程為絕熱過程，不考慮熱效應；

5)忽略重力加速度、空氣阻力以及靶板的整體運動；

6)忽略尾翼碰擊靶板時產生的沖擊；

7)彈丸和靶板初始應力均為零。

建模時，為了節省計算時間，對彈丸和靶板取1/2模型，靶板厚度按實際靶板厚度(180 mm)進行建模，在模型對稱面施加反對稱約束，在靶板周圍定義無反射邊界，模型單元類型選用八節點六面體單元，網格劃分采用映射網格法，模型計算采用拉格朗日法，引信頭與靶板之間采用面-面侵蝕算法，其余各零件之間的接觸采用面-面自動接觸，模型計算單位為g·cm·μs。火箭彈大著角碰擊靶板的有限元模型如圖5所示。

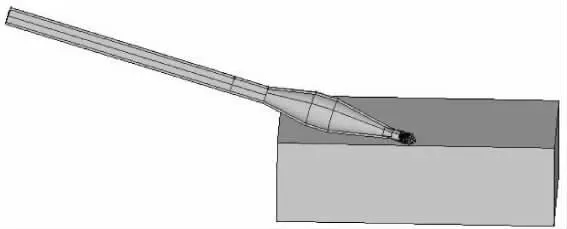
圖5 火箭彈大著角碰擊靶板的有限元模型Fig.5 The finite element model of rocket hitting target at large impact angle

2.3 材料模型

彈體材料采用30CrMnSiA鋼(按質量等效原則確定等效密度ρ)；引信頭、加強板和電極板材料為2A12鋁合金；陶瓷盒材料為T2；壓電陶瓷材料為GTQ-3；絕緣座材料為FX505壓塑料；絕緣墊材料為ABS樹脂；靶板材料為均質鋼。絕緣座和絕緣墊采用PLASTIC_KINEMATIC材料模型；壓電晶體采用JOHNSON_HOLMQUIST_CERAMICS材料模型；彈體、引信頭、電極板、加強板、晶體盒和靶板采用Johnson-Cook材料模型。各材料模型主要仿真參數如表1、表2和表3所列。

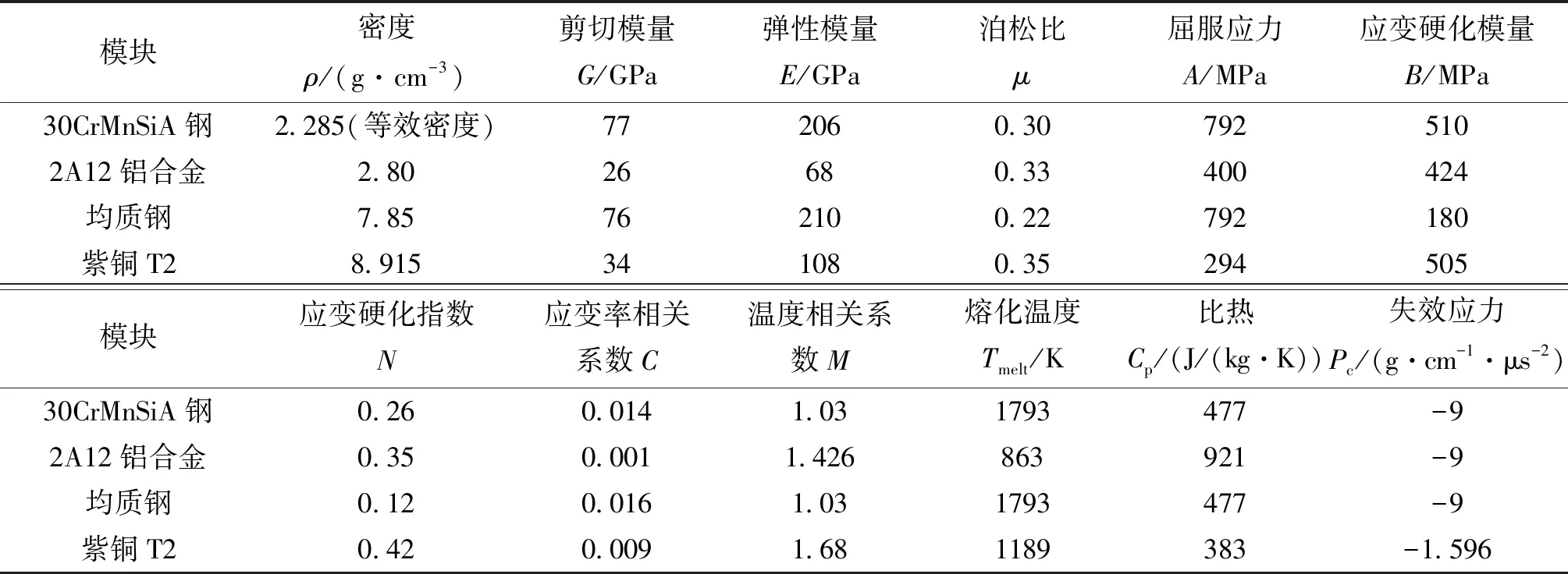
表1 Johnson-Cook材料模型主要參數[2, 7-9]Tab.1 The parameters of Johnson-Cook constitutive model

表2 PLASTIC_KINEMATIC材料模型主要參數[8]Tab.2 The parameters of PLASTIC_KINEMATIC material model

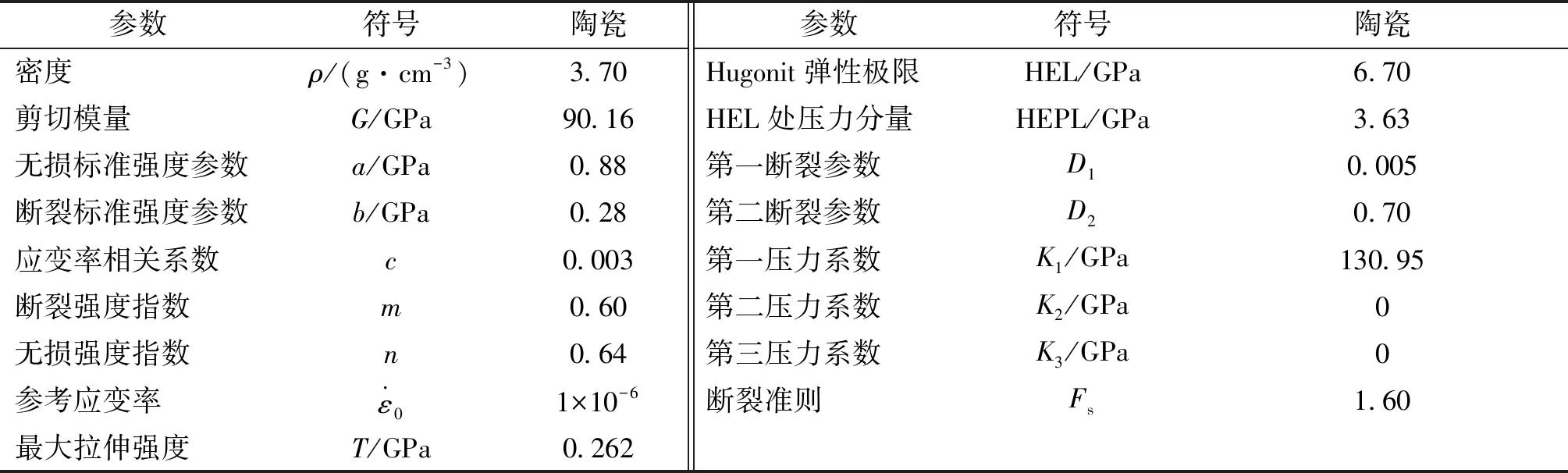
表3 JOHNSON_HOLMQUIST_CERAMICS材料模型主要參數[10]Tab.3 The parameters of JOHNSON_HOLMQUIST_CERAMICS material model

3 仿真結果及分析

3.1 引信頭結構對壓電晶體應力的影響分析

火箭彈以100 m/s，200 m/s，295 m/s三種不同的初速分別以55°，63°，68°，73°著角碰擊180 mm厚均質鋼靶板。為獲得不同引信頭結構作用于壓電晶體上壓電晶體應力的變化情況，擬定了圖6所示的四種不同引信頭結構方案，四種不同引信頭結構方案在仿真時所用材料都為2A12鋁合金。

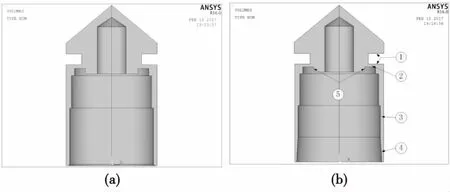
圖6 四種不同結構的引信頭有限元結構模型Fig.6 The finite element models of fuze head with different structures

方案一為目前制式單兵火箭彈所采用的結構，其引信頭頭部錐角為100°，見圖6(a)。

方案二在方案一基礎上修改，減小位置1處環形槽的寬度(由原3.2 mm減小為3.0 mm)，在位置2處加厚(由原0.6 mm增大到0.8 mm)，在位置3處減薄壁厚(由原0.95 mm減小到0.90 mm)，在位置4處加錐角，在位置5處減小凸臺直徑(由原14.4 mm減小到14.0 mm)并對位置5處凸臺圓弧加倒角(C0.5)，見圖6(b)。

方案三在方案二的基礎上修改，在圖中標識部位加圓弧過渡處理(過渡圓弧R2)，見圖6(c)。

方案四在方案一的基礎上修改，在圖中標識部位加圓角或倒角(R0.5 mm或C0.5)，見圖6(d)。

為了避免仿真過程中計測壓電晶體應力時所選壓電晶體單元數量對仿真結果的影響，以圖6(a)所示的方案一引信頭結構為研究對象、引信頭材料選用2A12鋁合金，彈丸以295 m/s的碰靶速度分別以55°，63°，68°，73°著角碰擊180 mm厚均質鋼靶板。仿真計測應力時所選壓電晶體單元方案分別如圖7(a)、圖7(b)和圖7(c)所示，所選壓電晶體單元為緊靠引信頭部壓電晶體表面上的單元，對應的壓電晶體單元數量分別為11個、25個和38個。仿真所得三種方案中計測應力所選壓電晶體單元上法向應力峰值平均值和等效綜合應力峰值平均值如表4所列。

圖7 仿真計測應力時所選壓電晶體單元Fig.7 The chosen piezoelectric ceramics elements for stress measurement

表4 仿真計測應力時所選不同壓電晶體單元上應力峰值平均值Tab.4 The average of stress peak calculated for different piezoelectric ceramics elements

從表4可看出：三種方案的計測壓電晶體單元上的應力平均值雖然在數值上存在一定差異，但都隨著角的增大而減小，仿真結果規律性一致。所選計測單元數量增多，雖然更能體現整個壓電晶體表面的應力值，但是數據處理所耗時間長，因此在對結論不會產生影響的前提下，應該選擇合適的單元數量對仿真結果進行處理。

影響計測應力所選壓電晶體單元上應力峰值準確性的主要因素是數據采樣時間間隔，而與仿真數據采樣時間間隔密切相關的是仿真計算結果輸出文件d3plot的輸出時間間隔，對應的關鍵字為“DATABASE_BINARY_D3PLOT”。為了避免所設置的仿真計算結果輸出文件d3plot的輸出時間間隔參數影響仿真結果，分別取時間間隔0.01 μs，0.02 μs，0.05 μs，0.2 μs，0.4 μs，0.6 μs，0.8 μs和1.0 μs進行仿真。仿真模型采用圖6(a)所示的方案一引信頭結構、材料選用2A12鋁合金，彈丸以295 m/s速度分別以55°，63°，68°，73°著角碰擊180 mm厚均質鋼靶板。仿真中計測應力所選壓電晶體單元選擇圖7(a)中方案，仿真所得計測應力所選壓電晶體單元上法向應力峰值平均值和等效綜合應力峰值平均值如表5所列。

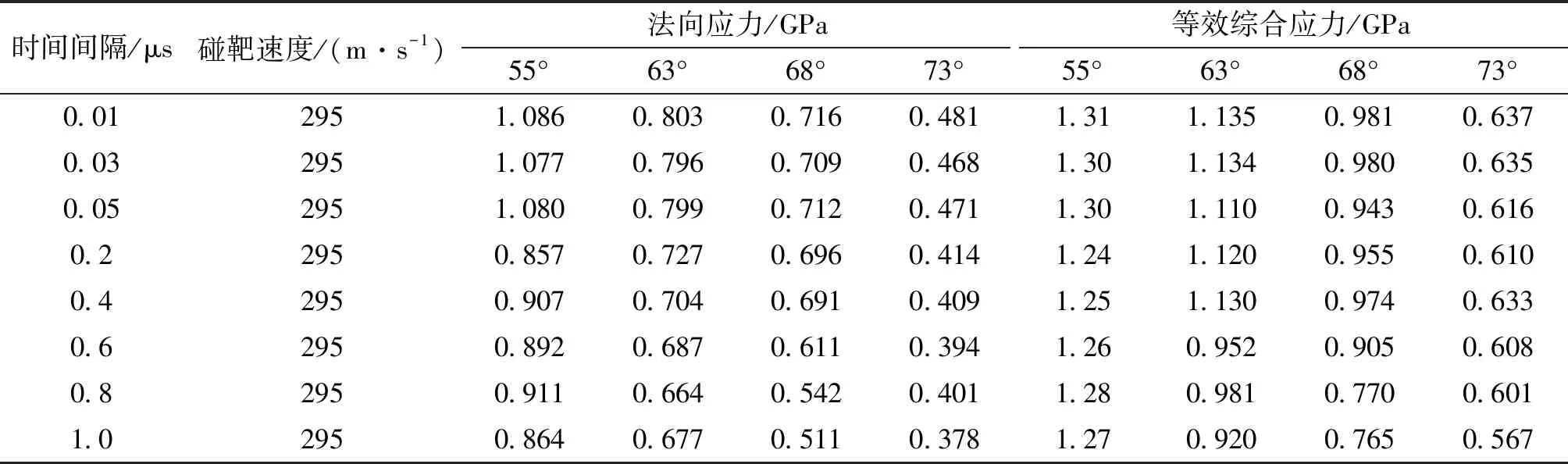
表5 不同時間間隔下仿真所得計測應力時所選不同壓電晶體單元上應力峰值平均值Tab.5 The average of stress peak of piezoelectric ceramics elements using different output frequency

從表5可看出：在相同速度、不同著角情況下，隨著數據采樣時間間隔的縮小，計測應力時所選壓電晶體單元上的法向應力平均值和等效綜合應力平均值總體上呈現增大趨勢，當所取時間間隔精度達到一定時，時間間隔精度不再影響仿真結果。在數據采樣時間間隔相同情況下，隨著著角的增大，計測應力時所選壓電晶體單元上的法向應力平均值和等效綜合應力平均值逐漸減小。當數據采樣時間間隔從0.05 μs，0.03 μs，0.01 μs變化過程中，所得仿真結果已經趨于穩定，其中0.05 μs與0.01 μs計算結果誤差在4%以內，說明所取數據采樣時間間隔基本不會影響仿真結果，所取時間間隔為0.05 μs時能夠滿足計算精度要求。因此以下仿真中計測應力時所選壓電晶體單元采用圖7(a)所示方案、數據采樣時間間隔為0.05 μs。

表6為上述四種不同引信頭結構分別以55°，63°，68°，73°著角碰擊180 mm厚均質鋼靶板時仿真得到的壓電晶體上各壓電晶體單元(對應圖7(a)所示壓電晶體上所選的壓電晶體單元)的應力峰值平均值。其中法向應力峰值對應壓電晶體單元上的正應力σ3，而等效綜合應力即Von Mises應力是基于剪切應變能的一種等效應力。

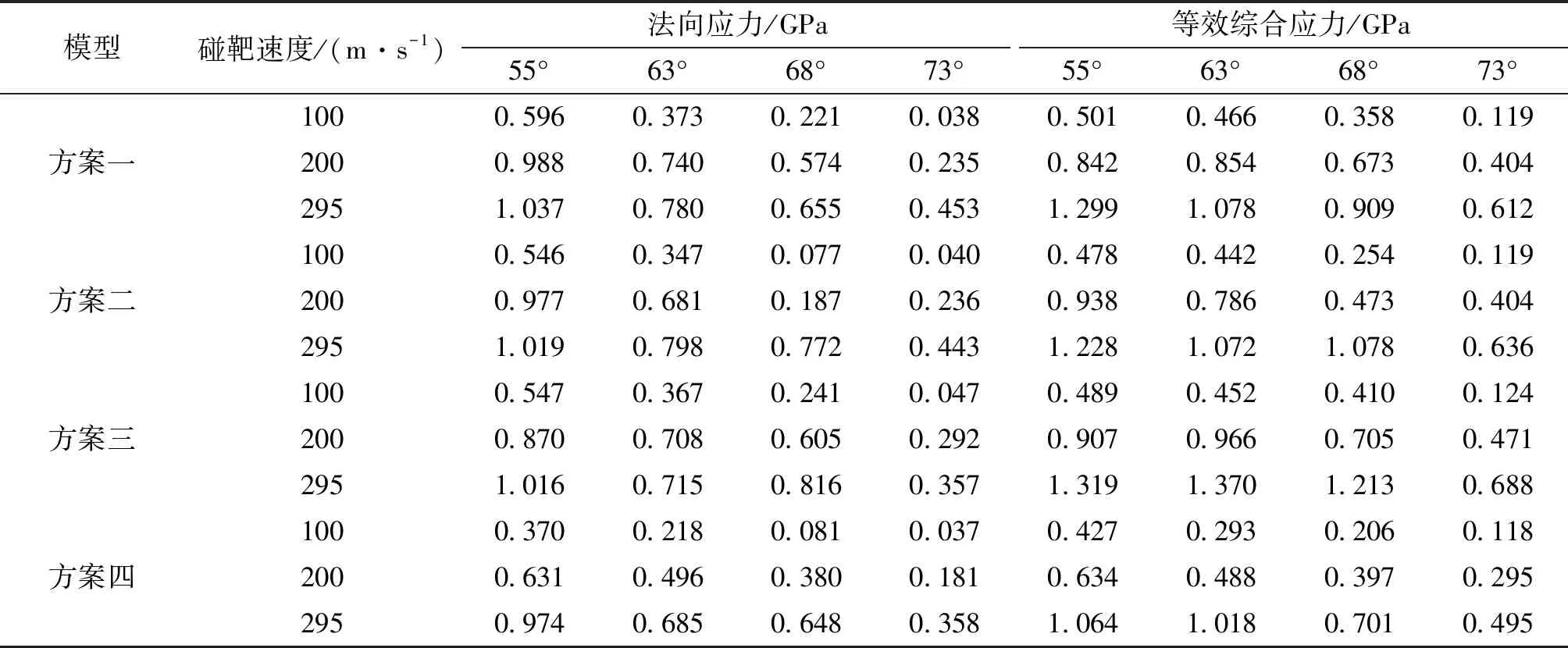
表6 不同結構方案以55°，63°，68°，73°著角碰擊均質鋼時壓電晶體單元上的應力峰值平均值Tab.6 The average of stress peak value of piezoelectric ceramics elements in different structural designs with various impact angles

由表6可看出：

1)在上述四種方案中，同種結構的引信頭在相同速度下分別以55°，63°，68°，73°著角撞擊均質鋼靶板時，壓電晶體單元上的法向應力值和等效綜合應力值都隨著角的增大而減小，與文獻[5]中結論一致，說明仿真是可信的。

2)同種結構的引信頭結構在相同著角下分別以100 m/s，200 m/s，295 m/s初速撞擊均質鋼靶板時，壓電晶體單元上的法向應力值和等效綜合應力值都隨著角的增大而減小。

3)對比三種改進方案即方案二、方案三和方案四中的法向應力值和等效綜合應力值可以得出：三種改進方案在碰擊著角大于55°時壓電晶體單元法向應力和等效綜合應力值均比原結構的要小，也就是說，通過改變引信頭部結構難以有效改善在大著角情況下引信頭作用于壓電晶體上的應力值，原結構及其參數設計已經處于優化狀態。

4)在數值仿真中，壓電晶體單元法向應力值和壓電晶體等效綜合應力值都可以反映出壓電晶體所受應力的變化規律。

3.2 引信頭錐角對壓電晶體應力的影響分析

為驗證引信頭部錐角變化對壓電晶體單元應力的影響，本次仿真在方案一結構基礎上改變引信頭頭部錐角大小，分別以80°，90°，98°，99°，100°，101°，102°和110°共八種不同錐角進行數值仿真，仿真結果如表7所列。

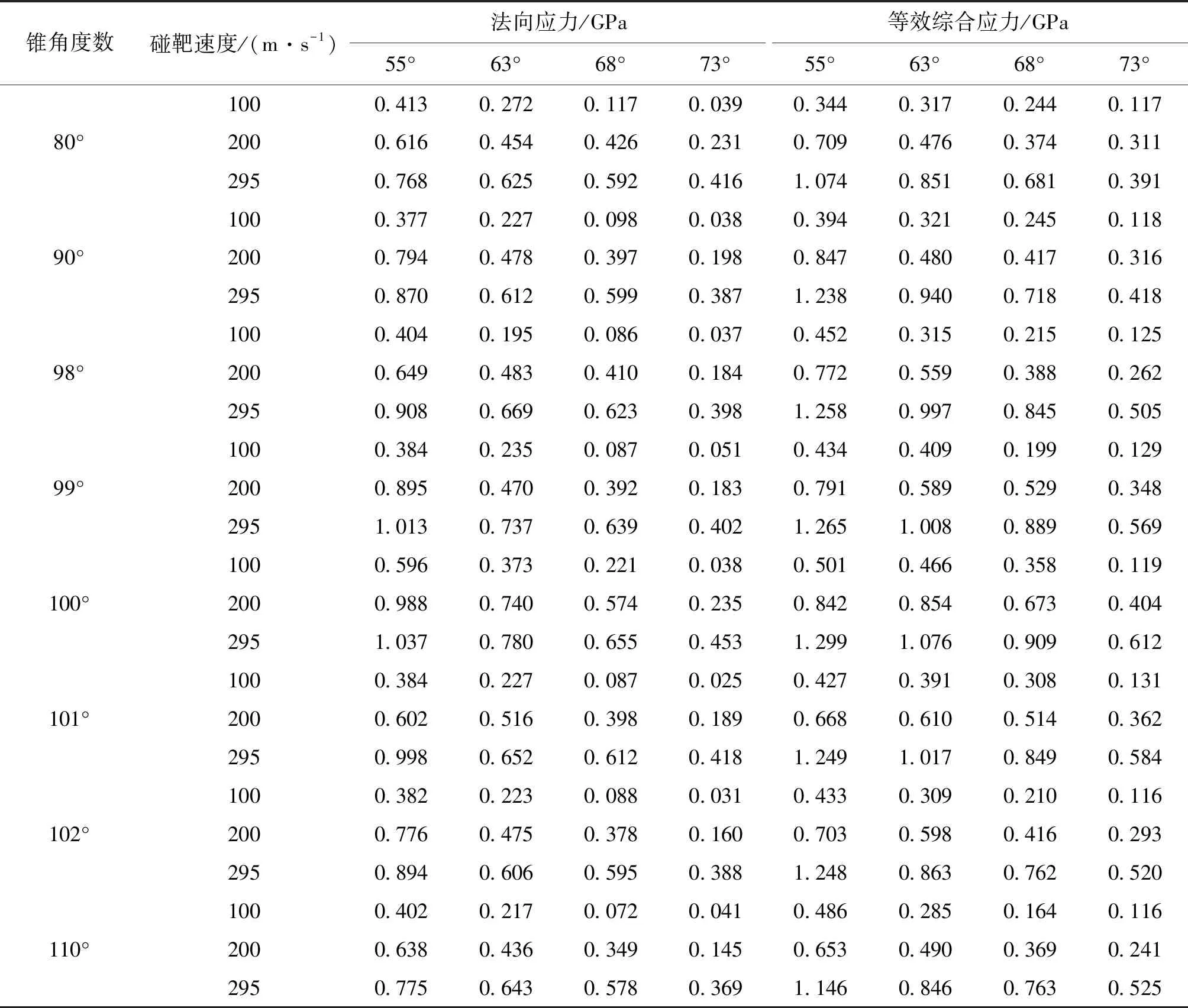
表7 不同頭部錐角以55°，63°，68°，73°著角碰擊時壓電晶體單元上的應力峰值平均值Tab.7 The average of stress peak value of piezoelectric ceramics elements in different head cones with various impact angles

從表7可看出，在大著角工況下，彈丸以相同著角、相同速度撞擊均質鋼靶板時壓電晶體單元法向應力以及等效綜合應力均隨引信頭部錐角的增大而出現先增大后減小的趨勢；彈丸以相同頭部錐角、相同初速撞擊均質鋼靶板時，壓電晶體單元法向應力以及等效綜合應力隨碰擊角度的增大而減小；在頭部錐角為100°時壓電晶體單元法向應力及等效綜合應力相對于其他錐角時的要大，也就是說引信頭部錐角存在最優錐角值，使得彈以不同碰擊角撞擊目標時壓電晶體單元的應力值達到最大。該頭部錐角即為原有結構設計參數，即100°。火箭彈以295 m/s初速大傾角撞擊均質鋼靶板時壓電晶體的應力隨撞擊角度的變化曲線如圖8和圖9所示。

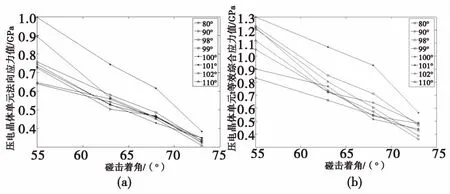
圖8 碰擊著角與壓電晶體單元法向應力和等效綜合應力值曲線Fig.8 The relationship between impact angle and normal stress and equivalent stress of piezoelectric ceramics elements

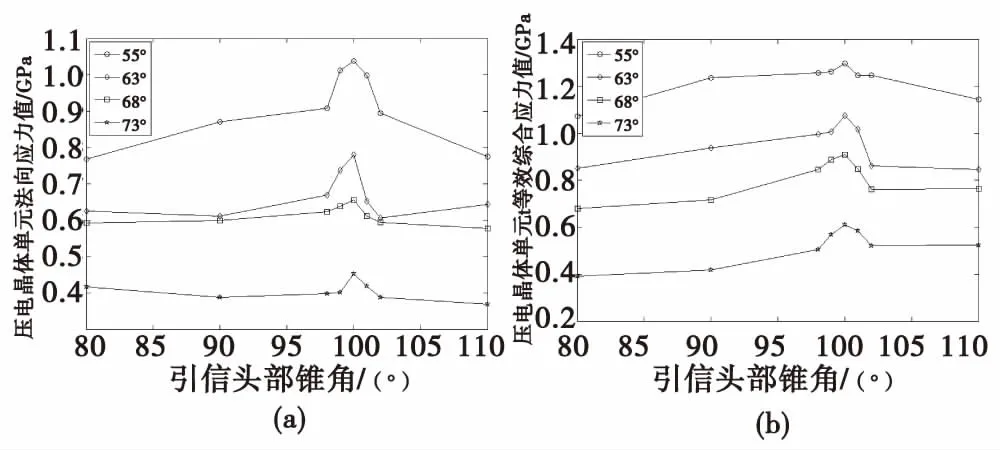
圖9 引信頭部錐角與壓電晶體單元法向應力和等效綜合應力值曲線Fig.9 The relationship between head cone angle and normal stress and equivalent stress of piezoelectric ceramics elements

3.3 引信頭材料對壓電晶體應力的影響分析

為驗證引信頭部材料對壓電晶體應力的影響，在方案一所示引信頭結構基礎上(引信頭部錐角為100°)，對頭部材料選用7種不同材料進行數值仿真，其中2A12鋁合金材料模型參數如表1所列，其余材料模型仿真參數如表8所列，仿真結果如表9所列。

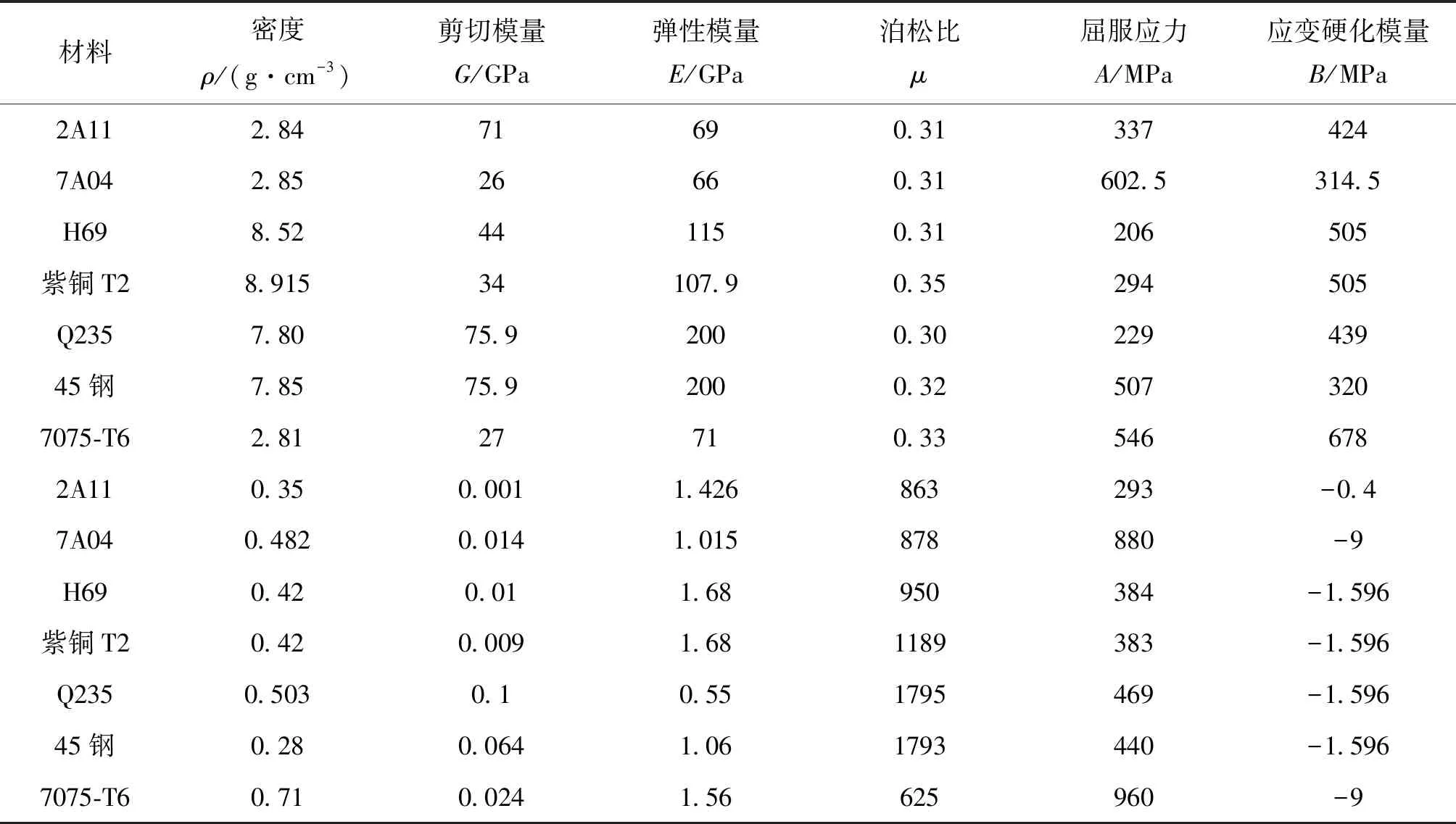
表8 Johnson-Cook材料模型主要參數[2, 7, 8, 11-15]Tab.8 The parameters of Johnson-Cook constitutive model

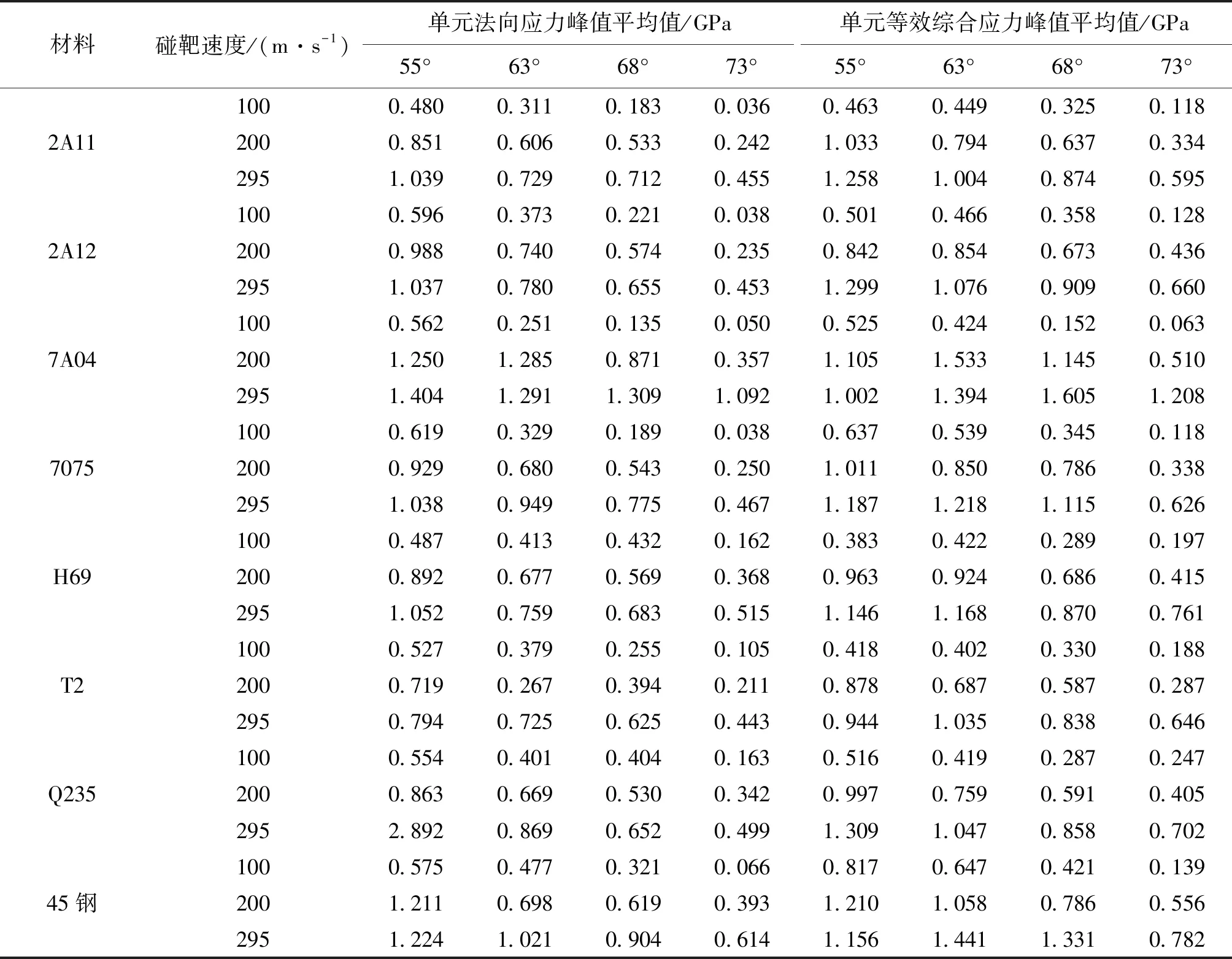
表9 不同引信頭材料時壓電晶體單元應力峰值平均值Tab.9 The average of stress peak of piezoelectric ceramics elements on fuze head with different materials

仿真結果表明，引信頭部材料為7A04時，在火箭彈初速為295 m/s并以不小于63°的碰擊著角碰擊均質鋼靶板時，引信壓電晶體上的應力值相比于其他幾種材料時的都要顯著偏大；同種材料的引信頭，碰擊速度對壓電晶體表面上的應力衰減影響較大，碰靶初速越大，在大著角工況下，壓電晶體表面上應力衰減量越小；不同材料的引信頭在相同速度下，2A11，2A12和7075材料引信頭對壓電晶體作用效果接近，但2A11和7075不如2A12；45鋼、Q235材料引信頭對壓電晶體的作用效果優于2A12但不如7A04，且45鋼及Q235密度較大，不太適用于輕武器；鉛黃銅H69對壓電晶體的作用效果優于紫銅T2，但兩者作用效果都不如2A12。從表9可看出，當7A04引信頭以63°，68°，73°法向著角碰擊均質鋼靶板時，壓電晶體上的應力值衰減較小。而對于其他幾種材料，隨著著角逐漸增大壓電晶體上應力值衰減較快，顯然對于大著角碰擊情形而言，7A04是壓電引信頭材料的最佳選擇。與原2A12相比，壓電晶體上的應力至少增大了30%。

4 結論

本文提出了壓電引信大著角發火性數值仿真方法。該方法通過比較仿真得到的壓電晶體上不同位置處壓電晶體單元的法向應力峰值平均值和等效綜合應力峰值平均值來對各種狀態、各種工況下的大著角發火正確性進行比較和判斷。仿真結果表明，隨著著角的增大，壓電晶體表面應力值呈現減小趨勢。在相同著角時，壓電晶體單元的應力值隨著碰擊初速的增大而增大，與理論分析結果一致，說明該方法可行。另外，改變引信頭部結構可以改變壓電晶體表面上的應力值，其中頭部錐角的變化對壓電晶體應力的影響較大；相同材料的引信頭，其頭部錐角在100°時壓電晶體單元應力值相對于其他角度錐角的壓電晶體上的應力值要大，也就是說，錐形壓電引信頭的頭部錐角最優值是100°(既有設計即取此值，說明已經優化，同時也說明本文仿真工作基本可信)，使得壓電引信在以大著角碰擊目標時，壓電晶體上的應力值達到最大；在相同速度下，引信頭材料2A11，2A12，7075和H69對壓電晶體作用效果接近，但2A12略優于2A11，7075和H69；Q235，45鋼對壓電晶體作用效果優于2A12，但不如7A04。但Q235，45鋼密度較大，不太適用于輕武器；采用7A04鋁合金代替原有的2A12作為引信頭材料可以使大著角碰擊目標時壓電晶體表面的碰靶應力至少增大30%以上，這對引信保證大著角發火作用正確性、降低瞎火率具有一定的參考作用。