基于高度的阻力系數(shù)實時修正方法

楊小會，張 英，何江楊，于 良

(1.機電動態(tài)控制重點實驗室，陜西 西安 710065；2.山東特種工業(yè)集團有限公司，山東 淄博 255200)

0 引言

彈道修正是彈藥實現(xiàn)精確打擊的重要途徑，快速準確地預測彈丸落點是實施彈道修正的前提。采用衛(wèi)星定位進行彈道測量，利用當前彈道參數(shù)結(jié)合理想的彈道模型外推實際落點是一種常用的落點預測方法[1]，空氣動力參數(shù)是彈道解算中的關(guān)鍵參數(shù)，其中阻力系數(shù)又尤其關(guān)鍵，其準確度直接影響落點預測精度。

實測數(shù)據(jù)表明，高空與地面的空氣密度和黏性系數(shù)差別很大，導致雷諾數(shù)的變化很大，如30 km高空上的雷諾數(shù)大約只有地面值的15%[2-3]，這使得彈丸的阻力系數(shù)增大，并且隨著高度的增加阻力系數(shù)增量也越大[4-5]。過去由于彈丸射程小，飛行高度不大，因此彈道解算中直接應(yīng)用在地面測得的阻力系數(shù)，不考慮隨飛行高度不同雷諾數(shù)變化的影響，解算誤差一般不大。然而現(xiàn)代彈丸的飛行距離和高度大為增加，例如155 mm復合增程彈飛行高度可達25～30 km，若不考慮雷諾數(shù)對阻力系數(shù)的影響則彈道解算誤差較大，射程誤差可達1%，已不能忽視[6]。

通常雷諾數(shù)對于阻力系數(shù)的影響采用風洞試驗獲得，但是只有在可變雷諾數(shù)、較高水平的風洞中才能實現(xiàn)，因此不容易獲取到不同雷諾數(shù)對應(yīng)的阻力系數(shù)。通過空氣動力計算軟件可以比較容易地獲取到不同彈道高度條件下雷諾數(shù)對應(yīng)的阻力系數(shù)，可以將雷諾數(shù)對阻力系數(shù)的修正轉(zhuǎn)換為高度對阻力系數(shù)的修正。針對不同彈道高度的氣象不同引起雷諾數(shù)不同，進而導致阻力系數(shù)不準確的問題，本文提出了基于高度的阻力系數(shù)實時修正方法。

1 雷諾數(shù)對阻力系數(shù)的影響

1.1 阻力系數(shù)計算方法

彈箭的阻力系數(shù)由零升阻力系數(shù)和誘導阻力系數(shù)組成，零升阻力系數(shù)Cx0主要由摩阻系數(shù)Cxf、渦阻系數(shù)Cxb和波阻系數(shù)Cxw組成[7]，見式(1)：

cx0=cxf+cxb+cxw

(1)

在紊流附面層條件下，彈丸的摩阻系數(shù)見式(2)：

(2)

式(2)中，Ss為彈丸側(cè)表面積，S為彈丸特征面積，ηλ為形狀修正系數(shù)，ηm為考慮到空氣的壓縮性后采用的修正系數(shù)。

Re為雷諾數(shù)，見式(3)：

(3)

式(3)中，ρ為空氣密度，μ為空氣的黏性系數(shù)，v為彈丸速度，l為彈體長度。

由于目前還沒有一個準確的計算渦阻的理論方法，因此采用工程算法[4]，將摩阻和渦阻合在一起計算，見式(4)：

cxf+cxb=Acxf+cxd

(4)

式(4)中，系數(shù)A與飛行馬赫數(shù)和彈丸長細比相關(guān)，Cxd為彈丸底阻，其計算方法見式(5)：

(5)

式(5)中，ξ為尾椎收縮比，λB為彈丸長細比，Ma為飛行馬赫數(shù)。

亞音速時波阻系數(shù)為零，超音速時，對于卵形頭部和截錐尾部彈丸波阻系數(shù)可采用式(6)估算：

(6)

式(6)中，φ0為彈頭半頂角，αk為尾錐角。

1.2 雷諾數(shù)對阻力系數(shù)的影響

由式(1)、式(2)、式(5)和式(6)可知，對于某一彈丸，在同一飛行速度時，不同的彈道高度對應(yīng)的空氣密度和空氣黏性系數(shù)不同，因此雷諾數(shù)不同，相應(yīng)的阻力系數(shù)就不同。圖1為不同高度對應(yīng)的空氣密度，圖2為不同高度對應(yīng)的雷諾數(shù)，圖3為不同雷諾數(shù)對應(yīng)的阻力系數(shù)，圖4為155 mm榴彈彈丸速度1.2Ma時不同高度對應(yīng)的阻力系數(shù)增量。由圖可以看出，高度增加20 km時，空氣密度和雷諾數(shù)約只有地面的10%，相應(yīng)的阻力系數(shù)增加了10%。

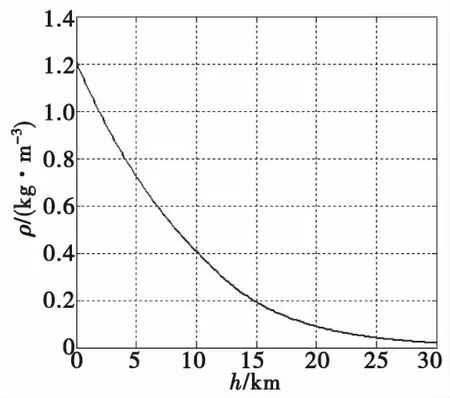
圖1 不同高度對應(yīng)的空氣密度Fig.1 Relation between air density and altitude

圖2 不同高度對應(yīng)的雷諾數(shù)Fig.2 Relation between Reynolds number and altitude

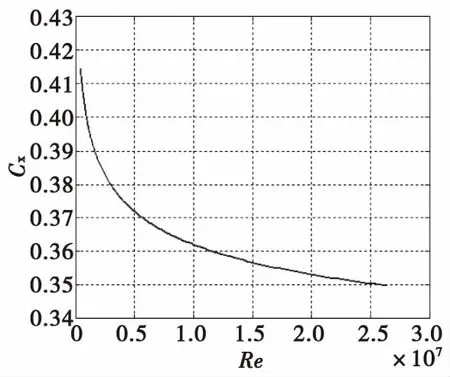
圖3 不同雷諾數(shù)對應(yīng)的阻力系數(shù)(Ma=1.2)Fig.3 Relation between Reynolds number and drag coefficient

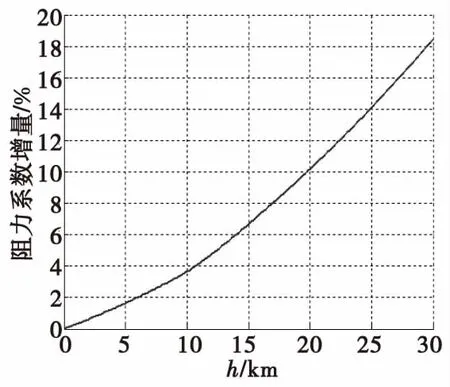
圖4 不同高度對應(yīng)的阻力系數(shù)增量(Ma=1.2)Fig.4 Relation between altitude and drag coefficient increment

2 基于高度的阻力系數(shù)實時修正方法

2.1 阻力系數(shù)與高度的關(guān)系

由式(2)和圖3可以看出，同一馬赫數(shù)下，阻力系數(shù)隨著雷諾數(shù)的增大而單調(diào)減小，阻力系數(shù)是雷諾數(shù)的反比例函數(shù)，如式(7)：

cx|Ma=g(Re)

(7)

由式(3)可以看出，雷諾數(shù)是氣象參數(shù)即空氣密度和黏度的函數(shù)，由圖1可以看出氣象參數(shù)是高度的函數(shù)，因此，雷諾數(shù)也是高度的函數(shù)，見式(8)。由圖2可以看出，同一馬赫數(shù)下，雷諾數(shù)是高度的反比例函數(shù)，即雷諾數(shù)隨著高度的增加而單調(diào)減小。

Re=f(h)

(8)

因此，根據(jù)式(7)和式(8)，可以將阻力系數(shù)與雷諾數(shù)的關(guān)系轉(zhuǎn)換為阻力系數(shù)與高度的關(guān)系，見式(9)。由如圖4可以看出，同一馬赫數(shù)下，阻力系數(shù)與高度成正比例關(guān)系，高度越高阻力系數(shù)越大。

cx|Ma=g(f(h))=k(h)

(9)

2.2 基于高度的阻力系數(shù)實時修正方法

圖5為155 mm榴彈不同馬赫數(shù)不同彈道高度對應(yīng)的阻力系數(shù)增量曲線。

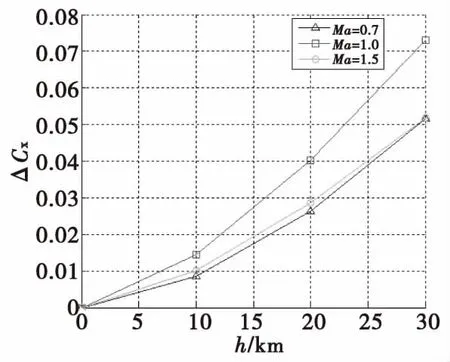
圖5 不同馬赫數(shù)不同彈道高度阻力系數(shù)增量Fig.5 Drag coefficient increment of different Ma and altitude

由圖5可以看出，同一高度下不同的馬赫數(shù)彈丸阻力系數(shù)增量并不相同，因此不同彈道高度下的阻力系數(shù)增量為彈丸飛行馬赫數(shù)和彈道高度的二元函數(shù)，見式(10)：

Δcx(Ma,h)=φ(Ma,h)

(10)

由圖5可以看出，同一馬赫數(shù)下，阻力系數(shù)增量與高度近似呈線性關(guān)系，因此將同一馬赫數(shù)下不同高度對應(yīng)的阻力系數(shù)增量進行擬合，可以得到高度與阻力系數(shù)增量關(guān)系，則式(10)可以變?yōu)槭?11)：

Δcx(Ma,h)=Kh(Ma)·h

(11)

式(11)中，Kh為相應(yīng)馬赫數(shù)對應(yīng)的高度對阻力系數(shù)的修正系數(shù)。

通過空氣動力計算軟件可以計算出地面不同馬赫數(shù)對應(yīng)的阻力系數(shù)Cx0(Ma)，則不同飛行馬赫數(shù)不同彈道高度對應(yīng)的阻力系數(shù)見式(12)：

cx(Ma,h)=cx0(Ma)+Δcx(Ma,h)

(12)

3 試驗驗證

以155 mm底排彈為平臺，采用仿真數(shù)據(jù)驗證基于高度的阻力系數(shù)修正方法的有效性。

3.1 高度對阻力系數(shù)的修正系數(shù)獲取

采用空氣動力計算軟件，通過設(shè)置不同馬赫數(shù)、不同高度對應(yīng)的氣象條件計算得到的阻力系數(shù)見圖6。將地面阻力系數(shù)作為基準，計算的不同高度對應(yīng)的阻力系數(shù)增量，進而得到高度對阻力系數(shù)的修正系數(shù)。修正系數(shù)的擬合采用萬米為單位，公式如下：

Δcx(Ma,h)=Kh(Ma)·h/10 000

(13)

擬合結(jié)果見表1。

表1 高度對阻力系數(shù)的修正系數(shù)Tab.1 Drag coefficient modified coefficient of altitude

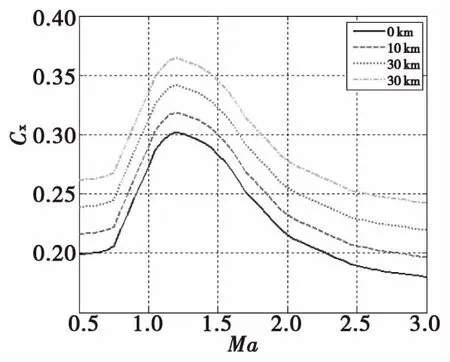
圖6 不同馬赫數(shù)不同彈道高度阻力系數(shù)Fig.6 Drag coefficient of different Ma and altitude

3.2 仿真驗證

以155 mm底排彈為平臺，在初速933 m/s，射角52°，4 500 m海拔氣象條件下(射程約55 km)，分別采用地面阻力系數(shù)和基于高度實時修正的阻力系數(shù)解算彈道，彈道曲線見圖7。由圖可以看出，基于高度實時修正的阻力系數(shù)解算的射距較采用地面阻力系數(shù)解算的射距近1 198 m，約2.14%，橫偏近43 m，約1.97%。

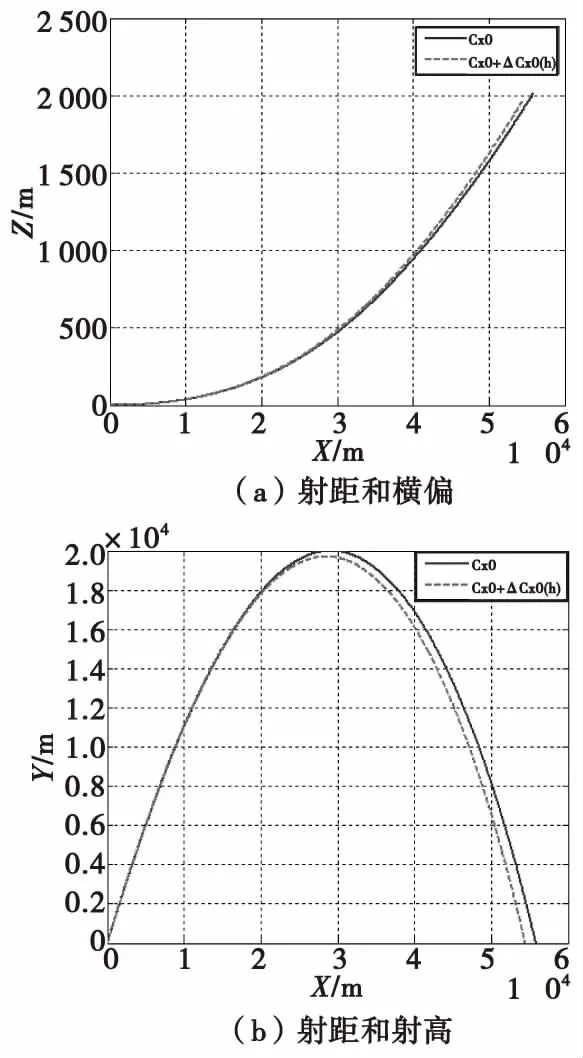
圖7 不同阻力系數(shù)解算的彈道曲線Fig.7 Trajectory of different drag coefficient

3.3 試驗驗證

基于155 mm底排彈全裝藥最大射程角外場試驗雷達跟蹤數(shù)據(jù)和實測氣象數(shù)據(jù)，分別采用地面阻力系數(shù)和基于高度實時修正的阻力系數(shù)，從彈道頂點時刻開始預測彈丸的落點坐標，將預測的落點坐標與實測的落點坐標進行比較，計算預測誤差，評估基于高度的阻力系數(shù)修正方法的有效性。彈丸的落點坐標見圖8。

由圖8可以看出，從彈道頂點時刻開始彈丸落點預測，采用地面阻力系數(shù)預測的落點誤差較大，5發(fā)彈丸射距誤差均值為87.2 m，橫偏誤差均值為62.0 m；基于高度實時修正的阻力系數(shù)預測的落點誤差較小，射距誤差均值為31.4 m，橫偏誤差均值為19.6 m，預測精度約提高了一倍。

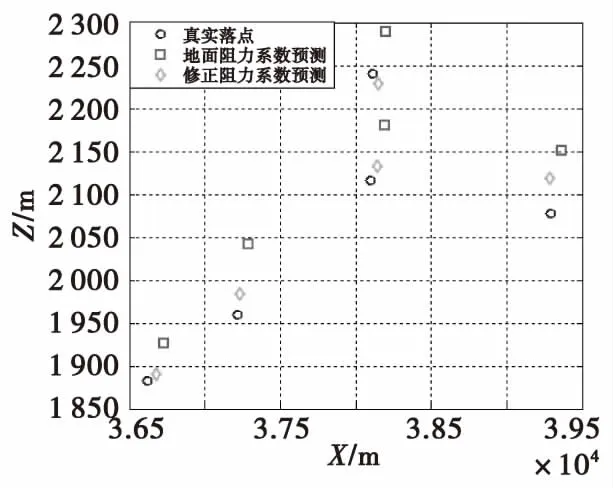
圖8 彈丸落點坐標Fig.8 Impact point of projectile

4 結(jié)論

本文提出了基于高度的阻力系數(shù)實時修正方法。該方法通過空氣動力計算軟件獲取到同一馬赫數(shù)不同高度氣象條件對應(yīng)的彈丸阻力系數(shù)變化量與高度的對應(yīng)關(guān)系，在彈道解算中，采用彈丸實際彈道高度插值該關(guān)系，實現(xiàn)了彈丸阻力系數(shù)的實時修正。155 mm榴彈底排彈最大射程角驗證結(jié)果表明：4500 m海拔時，高度修正的阻力系數(shù)對彈丸的射距和橫偏影響可達2%；從彈道頂點時刻開始彈丸落點預測，采用修正后的阻力系數(shù)較采用地面阻力系數(shù)的落點預測精度約提高了一倍。