基于張量投票的線性判別分析算法研究

李 姣，張成毅，羅雙華

(西安工程大學 理學院，西安 710048)

隨著大數據爆發式的增長趨勢，如何從復雜、冗余的數據中提取有效信息成為現階段的一個研究熱點。人臉識別、姿態識別、指紋識別等生物識別技術對圖像數據中的生物特征數據進行處理，涉及對高維圖像數據的處理技術。在此過程中“維數災難”成為分析圖像數據的一個巨大挑戰。為了解決這一問題，就需要選擇和提取數據中的顯著特征，即剔除不相關和冗余的信息降低數據維數以提取有價值的特征數據。線性判別分析對處理由單個因素引起變化的數據效果明顯，卻無法滿足越來越復雜數據的處理需求。因此，多重線性代數的應用逐步彌補了這方面的缺陷。

線性判別分析在處理多類數據的分類及降維問題中取得了一定的顯著效果，但針對此過程中可能存在的小樣本問題，不同改進算法處理的核心思想也不同，如溫浩等人將LDA擴展到張量子空間下，提出了用張量線性判別分析(Tensor Linear Discriminant Analysis, Tensor-LDA)來進行人臉識別算法的研究[1]，但算法中存在低維特征提取不充分的問題。因此，本文在此基礎上提出了基于張量投票的線性判別分析算法，即首先使用張量投票對樣本數據即點、曲線和曲面等結構特征的提取，再利用線性判別分析進行分類和降維處理，以解決圖像數據中可能存在的小樣本問題。

1 張量投票方法

張量投票[2]是一種推斷圖像顯著結構的算法。計算流程可概括為三大步驟：(1)將輸入圖像數據的像素點轉換為張量表示；(2)每一個像素點的張量在其鄰域內傳播信息并收集傳播到自身的信息,計算的方式主要為兩次張量投票：第一次為稀疏投票，一般選擇球形投票域，只在輸入的數據點之間進行，投票結果會形成新的張量表示；新的張量再選擇合適的投票域進行第二次張量投票——稠密投票，即向圖像中的所有像素點投票,投票結果形成特征顯著圖；(3)根據數據的特征顯著度對投票結果進行特征提取，主要包含基于矩陣特征值計算的投票解釋和基于極值搜索的特征提取。[3]

如圖1所示，像素點的張量表示即在取向估計的基礎上根據各點的取向特征生成投票域；張量投票后對所有投票疊加，使各數據點形成新的張量表示；在投票形成新張量后需要對投票進行解釋即特征值的分解過程；特征提取即對點、曲線等顯著圖的搜索過程。[3-5]在張量投票算法的計算步驟中進行的兩次投票及最后的輸出均為張量形式，這可能會造成維數災難等問題，由于高維數據之間的運算雖然會避免數據結構信息的丟失，但需要花費大量的時間。

近幾年，張量投票算法逐漸與其他算法相結合用于解決涉及圖像處理方面的問題。例如，林洪彬等人針對張量投票理論無法進行解析求解的難題，提出了基于解析張量投票的散點云特征提取算法。[6]李慧嫻等人為了檢測物體表面裂痕，在檢測算法主體過程中為了得到完整的裂紋區域，使用張量投票得到了裂紋的中心線并以此作為連接裂紋片段的曲線，通過實驗驗證張量投票算法對裂紋片段進行了有效的連接和噪聲去除。[7]

2 線性判別分析

線性判別分析方法(LDA)在處理數據時需要預先知道樣本的類別并通過提取最有利于分類的特征，從而使得同類樣本聚合度好而不同類樣本離散度大。LDA以分離不同類別為目的，充分利用訓練樣本的已知類別信息尋找最有助于分類的最佳投影子空間，使得不同類別的數據樣本在這個子空間內彼此互相分離。LDA通過Fisher準則找到一個最優線性投影(轉換)矩陣，然后利用最優線性投影矩陣獲得最佳投影子空間。[8]

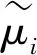
其中：Ni表示屬于第i類的樣本個數。

這一過程往往存在由于訓練樣本不足而引起的類內散度矩陣奇異的小樣本問題。Zhu M等人提出的子類判別分析(Subclass discriminant analysis)[9]和Gkalelis N等人提出的混合子類判別分析(Mixture subclass discriminant analysis)[10]，分別針對小樣本作了相應的改進并均取得了顯著的效果。而這些基于子空間的改進算法主要是通過在分類階段更加細化的表示樣本均值，但容易出現融合技術選擇的難題。

3 改進線性判別分析算法

基于上述兩種算法在處理具體問題時存在的不足，本文提出的基于張量投票的改進線性判別分析算法主要特點就是將張量投票對數據結構特征的魯棒性優勢融入線性判別分析中，從而取得較好的融合處理結果。算法的優勢主要是融合了兩者在處理圖像數據時各自具備的優點從而采取較好的處理方式：張量投票采用非線性的方法處理圖像數據中的顯著點、曲線和曲面等[11]；線性判別分析則采用線性原則對數據進行降維、分類處理[12-14]。因此，改進算法的提出將線性方法和非線性方法相結合，既解決了非線性方法在處理數據時存在的缺點,又解決了線性方法存在的不足。

改進算法的實現過程包括兩個階段：輸入待處理的數據到張量投票方法流程中進行處理，得到投票結果；將投票結果代入線性判別分析的判別準則函數中進行分類、降維處理，并輸出最終結果。

3.1 張量投票階段

張量投票方法的最大特點是輸入特征和輸出特征均使用張量表示，能夠從稀疏或噪聲掩蓋下的數據中推斷出結構信息。通過兩次投票將輸入數據的顯著性特征提取出來并用張量表示，實現數據模型的張量表示、投票域的計算以及數據通信的線性投票。[15]

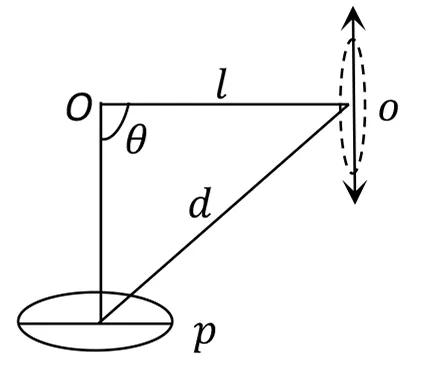
圖2 張量投票域示意圖

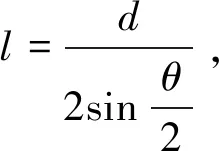
點P與周圍所有可能發生作用的點之間的連接曲線及其取向構成投票域的形狀及取向，投票的大小代表強度，二階對稱張量投票的投票強度衰減函數為：

其中：DF為投票域的投票強度,σ為投票尺度,s為弧長,κ為曲率,c為投票尺度σ的函數，用于調整距離和曲率對投票大小影響的比例關系，同時控制著投票域的橫向張度。

投票強度衰減函數表明了投票大小會隨平滑路徑的長度增加而衰減，并且傾向于保持直線方向的連續性。投票的尺度參數作為投票域的投票強度計算框架中唯一關鍵的參數，定義了投票鄰域的大小，并且是對曲線平滑程度的一種度量。[15]投票域的影響范圍介于小尺度和大尺度之間：小尺度范圍下的投票，過程更加局部化并且有利于保持圖像細節，但存在受外部干擾影響大的缺陷；大尺度范圍下的投票，過程可以連通一些斷點,抗噪能力強，不足之處在于圖像的平滑性容易受到影響。

如圖3所示，對邊界點作張量投票處理后得到了近乎封閉的曲線。這說明張量投票方法對邊界點鄰域之間的相關性作出投票，從而連接相關性較大的邊界點得到顯著曲線即圖像的大致形狀。在張量投票過程中主要使用了棒形投票域獲得最終的結果圖。從圖3中可以看出張量投票過程將lemon的邊界特征點提取出來并進行了光滑曲線的連接，較明顯地突出了張量投票對于顯著圖提取的魯棒性。第一張是輸入的邊界點圖像，在進行了張量投票處理后，從第二張可以看出算法連通了相關性大的斷點并形成了較為光滑的曲線圖像，但存在一定的噪聲數據。因此，接下來要做的就是將得到的結果張量代入線性判別分析中，以實現對于圖像數據的最后處理。

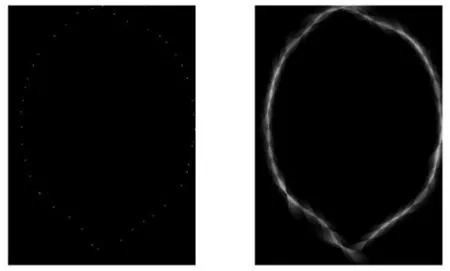
(a)dot-edge圖像 (b)TV圖像

3.2 線性判別分析階段

由于張量投票的最終結果是張量，具有較高維數，但最終的結果張量中包含著從輸入數據中提取的顯著特征，保存了輸入數據一定的結構信息。因此，在不破壞這種結構特征的基礎上將得到的結果張量代入線性判別分析中，求解降維處理后的張量子空間。待測樣本數據經過投影后在張量子空間中構成與待測樣本具有投影關系的新樣本數據，并且新樣本數據之間存在不同類的數據點之間相互分離、同類的數據點之間彼此靠近的關系。

張量線性判別分析方法是傳統線性判別分析方法在張量子空間上的擴展。它在張量域對樣本進行處理并提取樣本的特征。相比于向量，有效保留了樣本的結構信息，并且更充分地利用了收集到的信息，同時還避免了線性判別分析中存在的小樣本問題，提高了學習性能。[12]因此，改進的線性判別分析算法在運算過程中更加精確地保證了類間散度矩陣和類內散度矩陣之間的關系。相比與傳統LDA算法中通過求解判別準則函數尋求最優的投影向量的差異，本文則是尋求一系列投影矩陣(張量)ui(i=1,2,…，N)從而實現將高維的張量樣本轉化為低維的張量數據，同時滿足類間散度矩陣最大化、類內散度矩陣最小化。[16]其中，類內散度矩陣SW、類間散度矩陣SB和構成的判別準則函數描述分別如下：

(1)

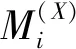
溫鳳文等人結合相似度量的概率學習方法，將兩個矩陣的相似度用屬于同一個集合的概率值來度量。并由條件概率公式定義兩個矩陣之間的差異集屬于同一集合的概率，文中用條件概率的高斯分布函數，即

估計條件概率

為樣本均值。[16]

對于投影后的樣本集UTXiV∈Rl1×l2，趙越等人針對投影矩陣U和V不能同時計算的問題，定義了兩個優化函數來確定U和V。[17]以其中的一個優化函數為例具體操作如下：對于一個固定的V，U通過優化函數J(U)來實現：

(2)

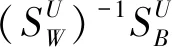
本文在兩者處理投影矩陣的方法中得到啟示，即針對投影矩陣不能同時計算的問題，引入貝葉斯定理實現對該問題的處理。通過對兩個投影矩陣之間先驗概率的學習，從而實現對相應后驗概率的表示。

(3)

雖然投影矩陣U和V不能同時計算，但貝葉斯定理將兩個投影矩陣之間通過先驗概率與后驗概率存在的關系表示出來。使用貝葉斯定理進行兩個投影矩陣之間關系的表示，主要是考慮到貝葉斯定理將兩個相關因素用已知概率表示，避免了在運算過程中丟失某些數據，同時也避免了小樣本問題的出現。

3.3 算法流程

提出的改進算法的主要流程為：

Step 1:輸入待處理圖像到張量投票流程中，進行初步處理，即將像素點張量表示后代入T=λ1e1e1T+λ2e2e2T,其中T為二維空間的二階對稱張量，λ1≥λ2≥0為T的特征值，e1和e2為對應的特征向量。通過相關的運算得到相應的特征值對應的特征向量構成的張量，然后輸出得到結果張量。

Step 2:通過將結果張量代入改進線性判別分析算法中，即代入式(1)中對類內散度矩陣與類間散度矩陣兩者之間在結果張量條件下構成的關系進行運算，從而得到相應的最優解。

Step 3:將投影矩陣U和V通過貝葉斯定理進行處理，即代入到式(3)，得到兩者之間的關系。

Step 4:對相應的優化函數作最優化處理，得到最終的最優解，即將U和V代入式(2)中，在不斷迭代的過程中尋求滿足迭代次數而獲取的最優解。

通過上述流程為改進算法的實現提供了理論支撐。在進行整個算法的過程中，存在的難點主要在于流程的第二步，即張量投票與線性判別分析的融合階段，在這個階段出現的問題可能會直接影響整個算法的效果。因此，在保證整個算法流程的流暢性的同時，本文著重改進了在張量投票過程中形成的結果張量代入線性判別分析流程后作為投影矩陣而產生的問題，即將投影矩陣存在的問題通過貝葉斯定理進行了處理。

在整個算法流程運行的過程中，通過規避每一步中可能存在的不足，將兩種方法各自處理圖像數據的優勢放大，在不足處作出相應的改進。如對于張量投票過程中產生的結構張量在代入線性判別分析過程中容易出現維數不匹配的問題，將貝葉斯定理代入其中作出改進，從而實現兩者之間的過渡。

4 實驗結果與分析

對于算法效果的實驗驗證主要選擇了簡單圖像的邊界點，即通過離散的邊界點獲取圖像的邊界形狀，依據離散點間存在的關系獲取預期的顯著曲線。實驗主要是在Matlab R 2016a環境下進行的。

實驗取得的結果如圖4所示。

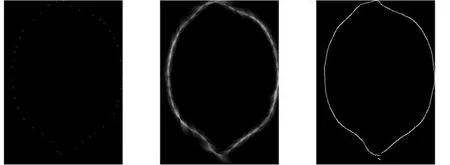
(a)dot-edge圖像 (b)TV圖像 (c)改進的邊界提取圖像

從圖4(c)可以看出，改進后的LDA算法融合了張量投票對于顯著點或曲線等特征提取的魯棒性，剔除了原本在張量投票過程中圖像數據中含有的噪聲數據，得到了比較好的圖像輪廓曲線。其中，圖4(a)為輸入圖像lemon的點邊界圖像，圖像中的點邊界提供了原圖像的全局形狀；圖4(b)為經過張量投票(Tensor Voting, TV)處理后的圖像，輸出的結果可以清楚地看出原圖像lemon的大致形狀，但邊緣存在一定的噪聲數據；圖4(c)為最終的輸出結果，本文提出的改進算法將原圖像lemon中含噪數據剔除后，在對圖像數據的進一步處理中保證了算法的穩定性，即保留了圖像的連續性。

以下幾種圖像在采用提取圖像邊界點來獲取邊緣圖像的算法與文中研究的改進算法之間的清晰度對比分析如表1所示。

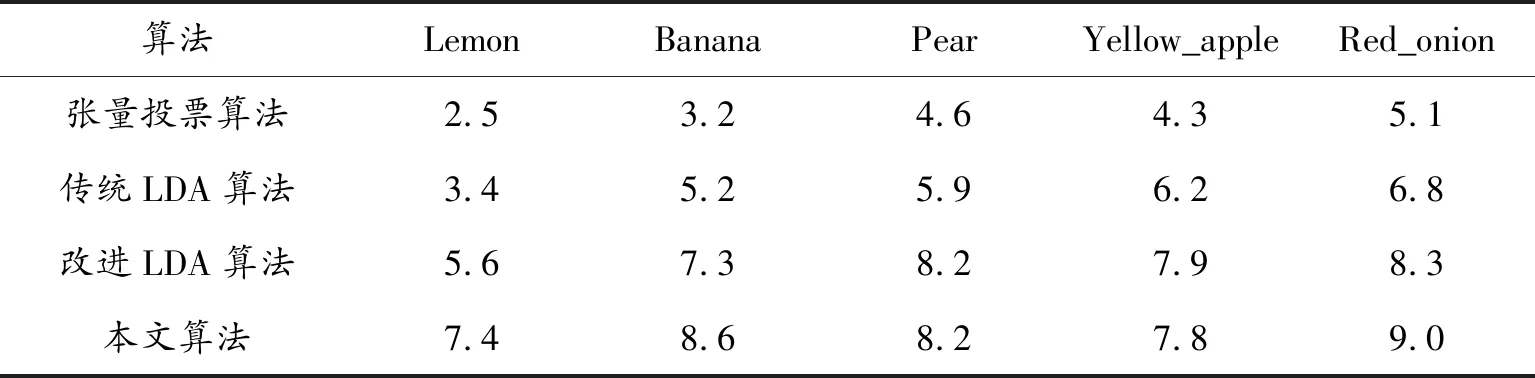
表1 幾種獲取邊緣圖像算法的對比

注：本文中指定識別圖像的邊緣圖像的清晰度分為：模糊[0,3]；較清晰(3,7]；清晰(7,10]

由表1的對比分析可知，對圖像的邊界點提取并形成近似封閉邊緣的處理中，對較為簡單的圖像邊界點的處理幾種算法都得到了較為清晰的邊緣圖像；對復雜及邊界點離散程度大的圖像提取的邊緣圖像效果較為模糊。

從實驗結果可以看出，與傳統LDA相比，本文提出的改進算法避免了將張量代入判別函數中存在的不能同時計算等問題。在算法實現的第一步就對待處理圖像進行了顯著特征的提取，在這一步主要是利用了張量投票對于圖像顯著性的魯棒性；對在下一步的線性判別分析階段只需要對處理后的圖像進行相應的降維和去噪處理。將這一系列處理流程中可能出現的問題也作出了相應的解決，實驗的最終結果表明改進的算法得到了對于圖像數據處理的預期目標。

5 結語

本文將改進的算法對簡單圖像的邊界點進行處理作為實驗驗證的基礎，取得的效果也比較理想。圖像數據的邊界點坐標在算法流程的實驗中得到了圖像的邊界曲線，主要在張量投票過程中逐步實現對點鄰域之間相關性的投票并得到了近似光滑的曲線圖像，圖像的整體特征曲線逐步顯現；將處理后得到的結果代入下一個階段即線性判別分析的算法流程中，經過相應的運算得到了含噪小、圖像邊界曲線近乎完整的實驗結果。

接下來的研究課題是不斷完善算法對于圖像數據處理的泛化性，使得算法對于復雜指紋圖像的識別也可以提取作為識別依據的顯著圖，并可以在指紋數據庫中作出一定的分類。在對簡單圖像的處理過程中，改進算法對于指紋圖像的處理可能存在的困難主要有指紋圖像具有紋理復雜、差異細微等特點，同時亟待處理的指紋圖像數據樣本也有二維或三維之分。因此，研究的課題為最終解決指紋數據的分類及識別的穩定性和高速率，就要求不斷改善提出算法的泛化能力，不僅對簡單圖像的處理具有很好的穩定性，也對復雜圖像數據具有較好的魯棒性。