擾流片式推力矢量噴管氣動特性數值模擬研究

叢戎飛, 吳軍強, 張長豐, 葉友達

(1. 中國空氣動力研究與發展中心 高速空氣動力研究所, 綿陽 621000;2. 中國空氣動力研究與發展中心 空氣動力學國家重點實驗室, 綿陽 621000;3. 國家計算流體力學實驗室, 北京 100191)

0 引 言

擾流片式推力矢量控制技術是通過將擾流片插入發動機尾噴流，利用擾流片上游的邊界層分離以及激波邊界層干擾等復雜的流動現象，使噴流相對噴管軸線發生偏轉來實現推力矢量控制。擾流片在未工作時位于尾噴流外緣，不接觸高溫燃氣，從而可以避免產生推力損失，減輕擾流片燒蝕。擾流片式推力矢量控制技術較為獨特，目前僅有俄羅斯的R-73導彈(圖1)及其衍生型號采用了這種控制方式。與目前先進空空導彈普遍采用的燃氣舵相比，擾流片具有非作用時無附加推力損失、響應快、控制力較大等突出優點，推力矢量角最大可達14°，在空空導彈、垂直發射導彈、以及彈射座椅等領域都具有廣闊的應用潛力[2-4]。 20世紀60年代起，Hollstein H J、Eatough R G等人針對擾流片式推力矢量控制技術進行了一系列冷噴流和燃氣噴流試驗，研究了擾流片形狀、安裝位置以及擾流片與噴管出口間隙對于側向力和推力 損失等參數的影響，為擾流片的工程應用奠定了理論基礎[5-9]。國內對于擾流片式推力矢量控制技術的研究起步較晚，研究手段以數值模擬為主，并進行了部分靜態及動態試驗研究[10-13]。

圖1 R-73導彈推力矢量控制系統Fig.1 Thrust vector control system of R-73 missile

目前國內針對該技術的研究尚停留在原理驗證以及有效性評估階段，與工程實用之間還有一定距離。為了滿足工程應用中對推力矢量噴管控制率建模以及優化設計的需求，本文將通過數值模擬手段，針對圓形、弧頂矩形以及扇形這三種擾流片外形，系統性的研究擾流片幾何形狀對噴管推力矢量特性的影響規律，建立氣動數據庫，為該項技術的工程化提供參考，為擾流片氣動優化設計做鋪墊。

1 擾流片式推力矢量控制技術原理

擾流片上游流場結構如圖2所示。當擾流片伸入噴管出口流場時，將會阻塞部分出口面積，直接導致在噴管的擴張段內產生斜激波，并伴隨有邊界層分離，而激波后分離區的壓力遠遠大于擾動前的壓力，將會在噴管內壁面產生非對稱壓力分布，從而產生側向力[14]。而斜激波與弓形激波在擾流片迎風面形成高壓區，使擾流片受到了與噴管推力方向相反的作用力，從而引起了噴管的推力損失。

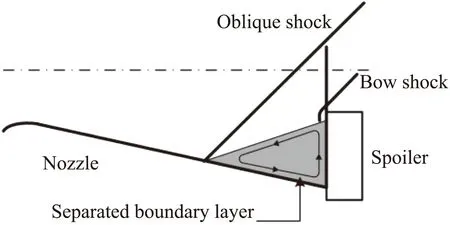
圖2 流場結構示意圖Fig.2 Shock profile

推力矢量分析如圖3所示。FAO為擾流片未插入時的初始軸向推力。FR為擾流片插入后的總推力，FA為軸向推力，FS為側向力。將總推力FR與噴管軸線的夾角θ定義為推力矢量角，可表示為：

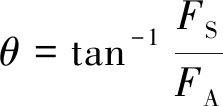
同時，為了評估擾流片引起的推力損失，定義推力損失系數η：

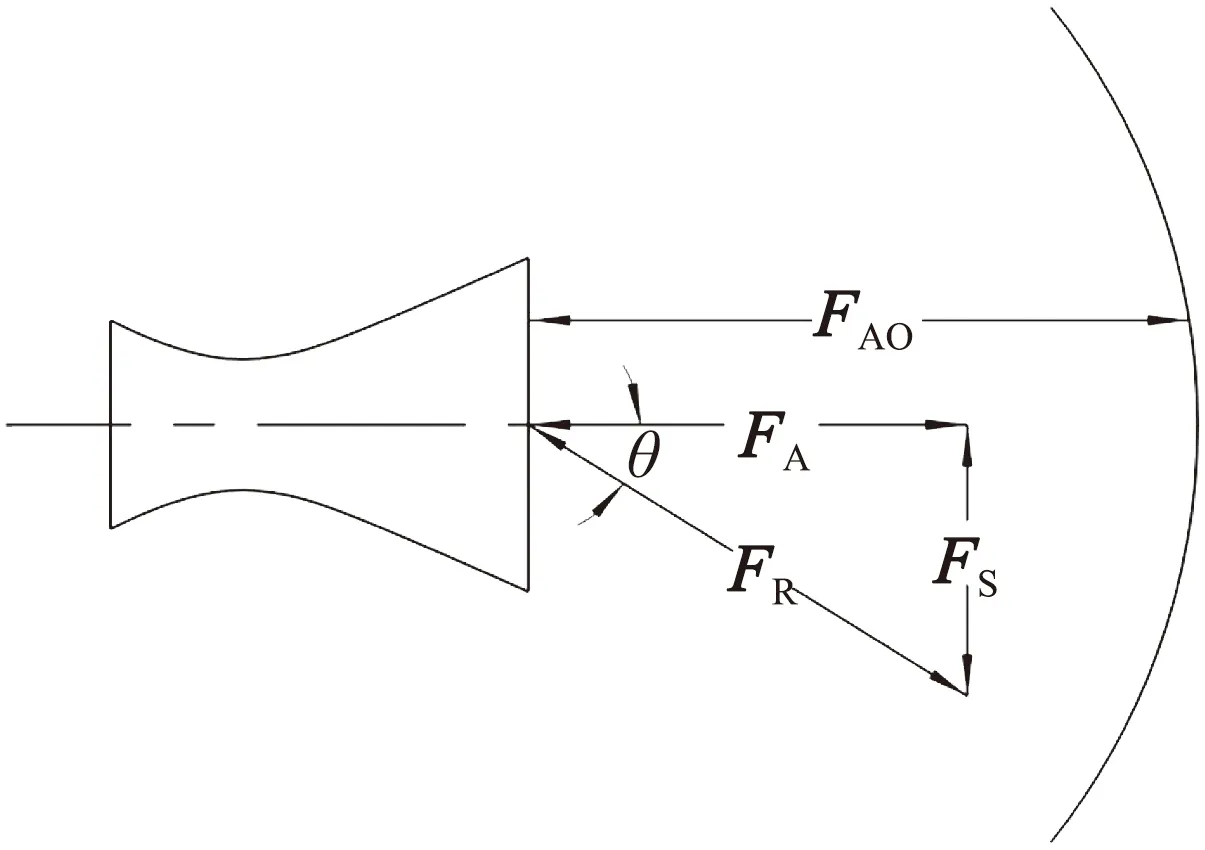
圖3 推力矢量分析Fig.3 Force relationship

推力矢量角描述了擾流片產生的側向控制力的大小，推力損失系數描述了擾流片工作時引起的推力損失的大小。本文將選取推力矢量角及推力損失系數作為衡量推力矢量特性的主要參數，對數值模擬結果進行分析和評估。在進行擾流片設計時，應使這兩個參數滿足側向控制力以及及推力的需求。

噴管的推力矢量通過公式(3)進行計算。

F=∑[ρv(v·N)+(p-p∞)N]ΔA(3)

其中:v為出口截面微元處燃氣的平均速度，p為出口截面微元的平均壓強，p∞為環境大氣壓強，N為出口截面微元的單位矢量。

2 數值模擬方法與驗證

2.1 數值模擬方法

使用計算流體力學商業軟件Fluent進行數值模擬，選用求解雷諾平均Navier-Stockes方程的求解器；空間離散方法為有限體積法，無粘通量采用Roe格式進行離散，粘性通量采用中心差分格式離散，時間推進方法采用LU-SGS(Low Upper Symmetric Gauss Seidel)隱式方法。湍流模型采用了二方程的Realizablek-ε模型，壁面附近采用標準壁面處理[15]。

2.2 數值模擬方法驗證

論文為了驗證本文數值模擬方法的準確性和有效性，選取美國推進實驗室的某軸對稱噴管進行數值模擬。噴管膨脹面積比為6.60。入口總溫為 294.3 K，落壓比為10，出口為大氣環境[16]。

數值模擬結果與文獻[16]中試驗結果的對比如圖4所示。圖中：p0為噴管入口總壓，p為當地靜壓，X為橫坐標，XL為噴管擴張段長度。從圖中可以看出，數值模擬結果與試驗結果吻合較好。

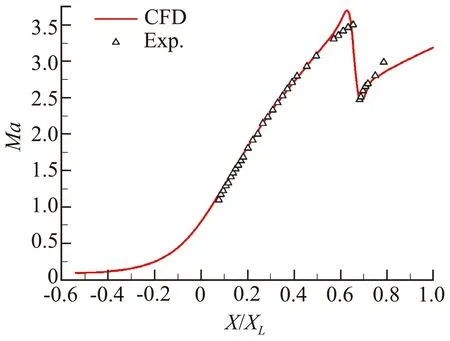
(a) 噴管軸線馬赫數

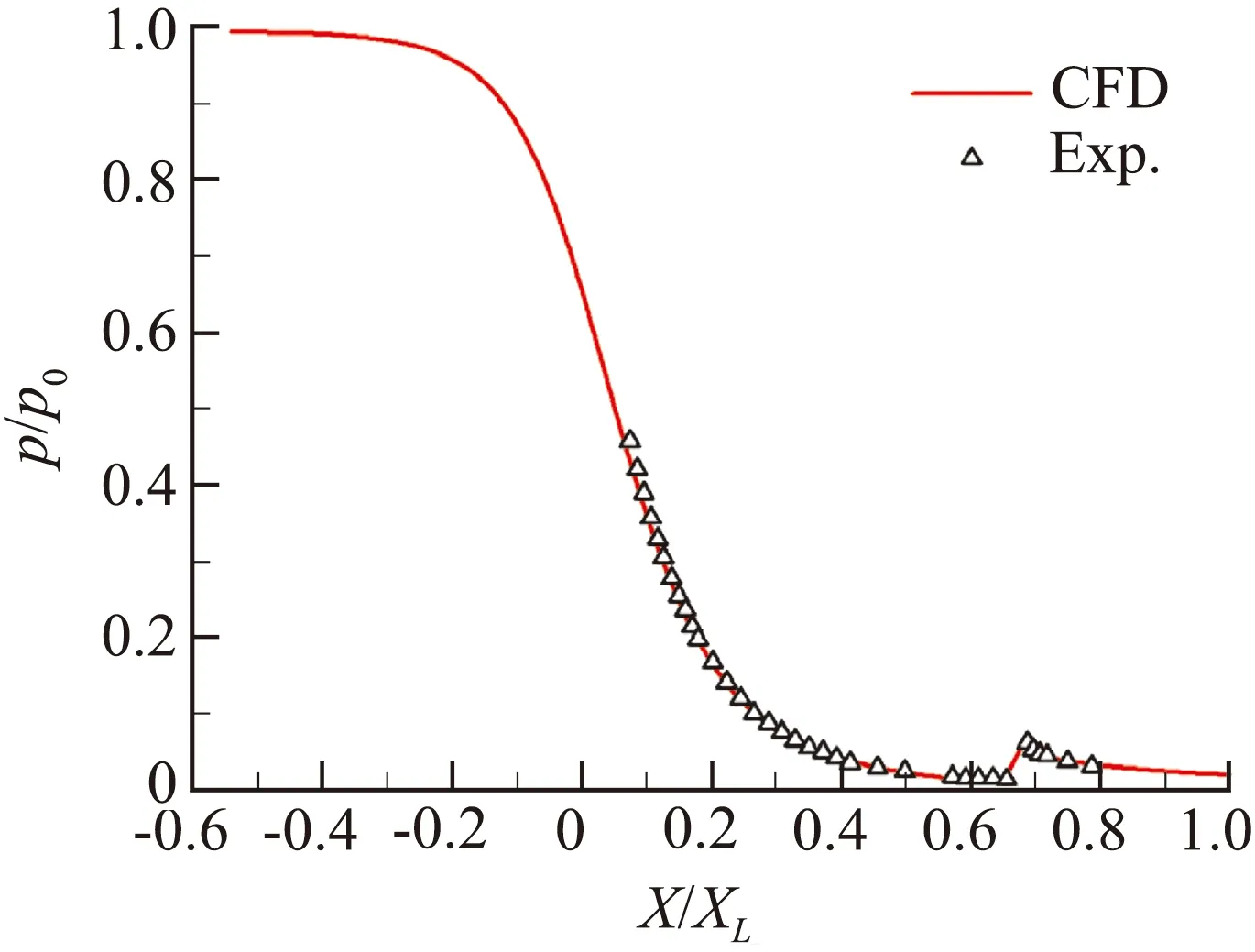
(b) 噴管軸線壓力

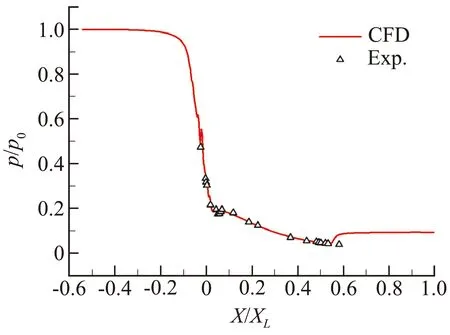
(c) 噴管壁面壓力

2.3 計算模型及邊界條件

數值模擬采用的基準軸對稱噴管的母線形狀如圖5所示。噴管膨脹面積比為6.25，設計落壓比NPRD=67.2。在噴管出口處添加不同形狀的擾流片，即構成了簡化后的擾流片式推力矢量裝置幾何模型。

圓形擾流片幾何模型如圖6所示。h為擾流片插入高度，選取h=0、2、4、6、8 mm五個狀態進行數值模擬，分析擾流片插入高度h對噴管內流特性的影響。

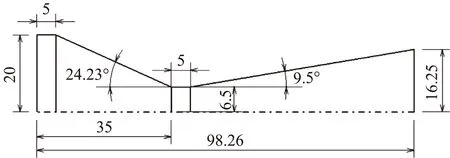
圖5 噴管母線(單位：mm)Fig.5 Sketch of the nozzle(unit: mm)

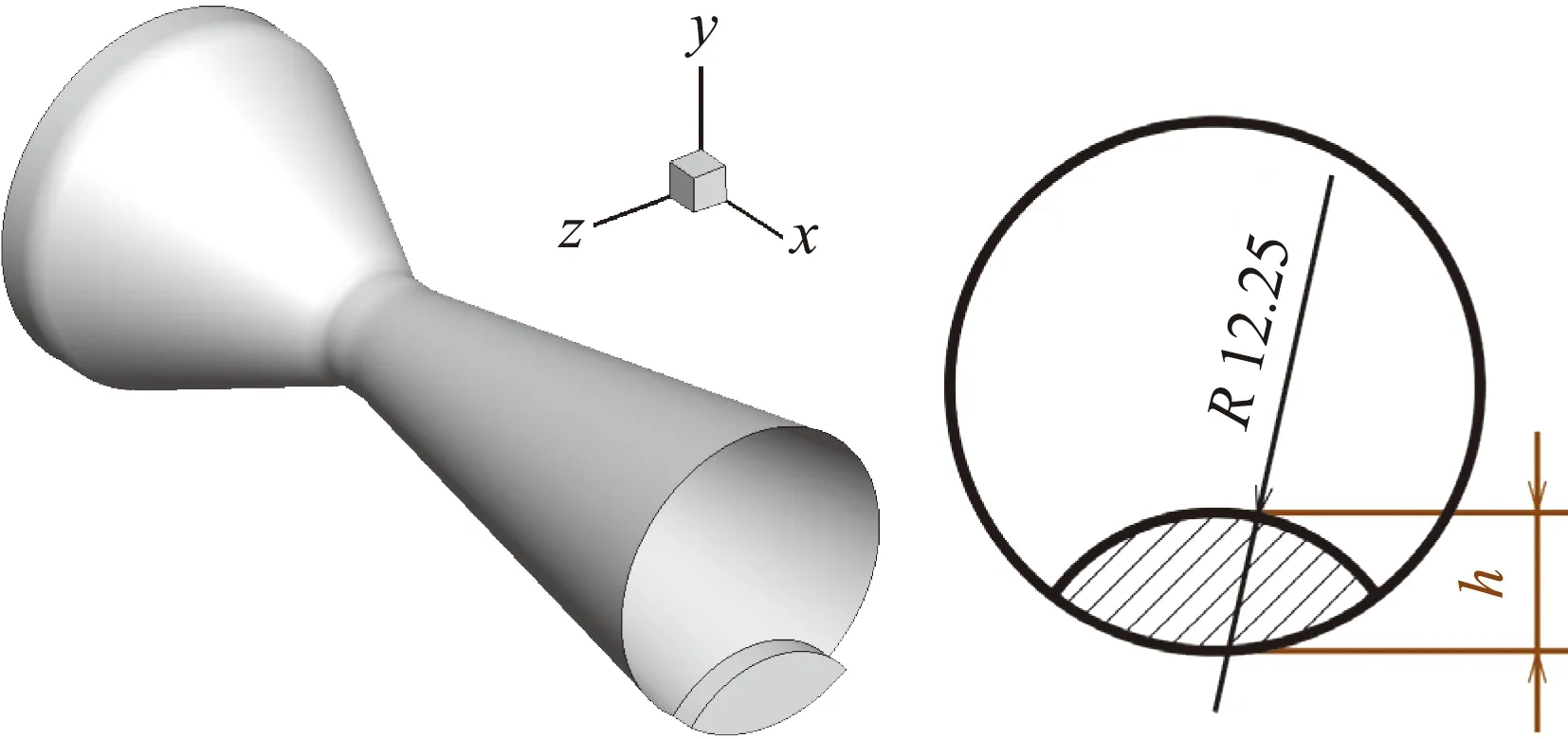
圖6 圓形擾流片幾何模型(單位：mm)Fig.6 Round spoiler (unit: mm)

弧頂矩形擾流片的幾何模型如圖7所示。擾流片的寬度d為設計變量，本文將針對不同寬度的弧頂矩形擾流片進行數值模擬。數值模擬狀態見表1。

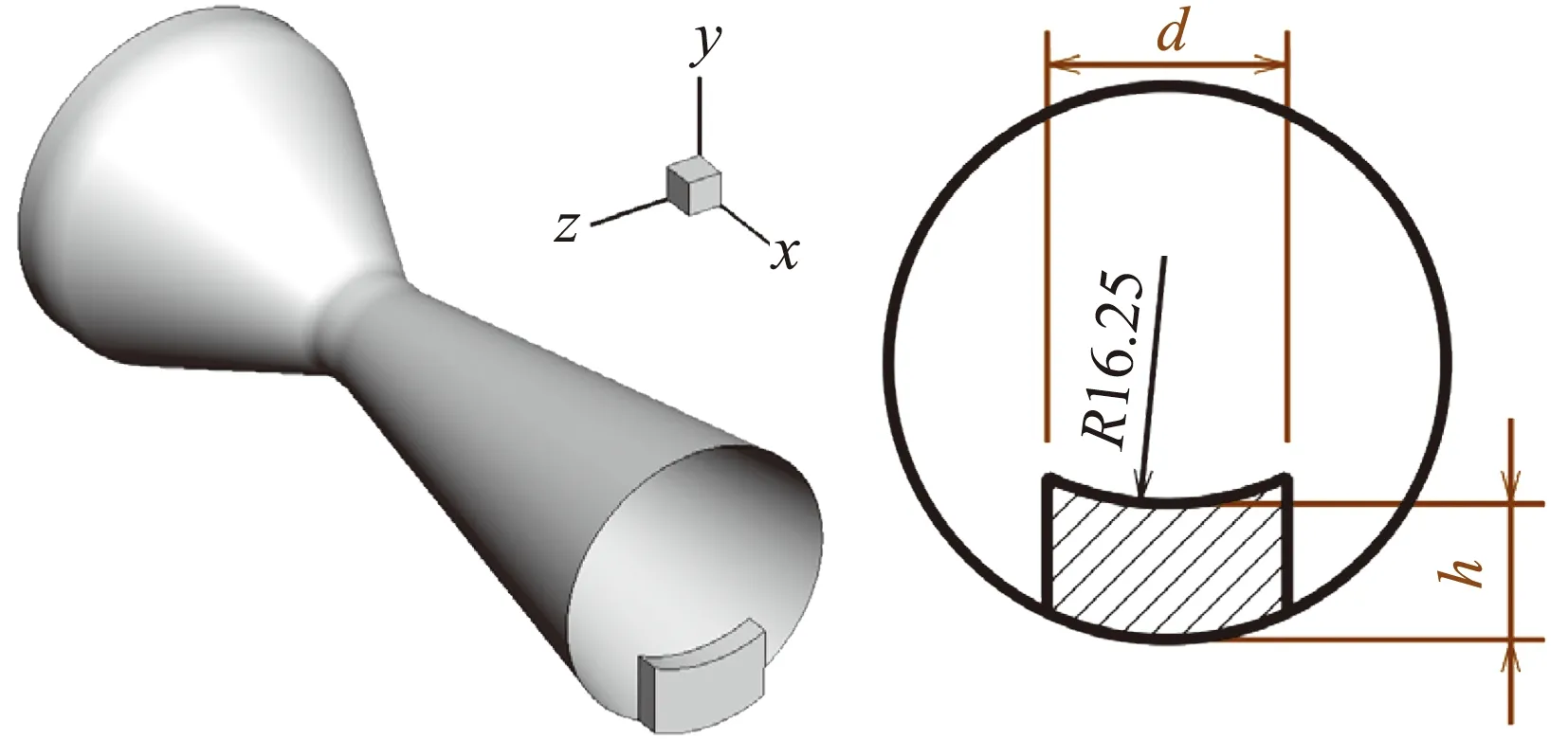
圖7 弧頂矩形擾流片幾何模型(單位：mm)Fig.7 Rectangle spoiler (unit: mm)

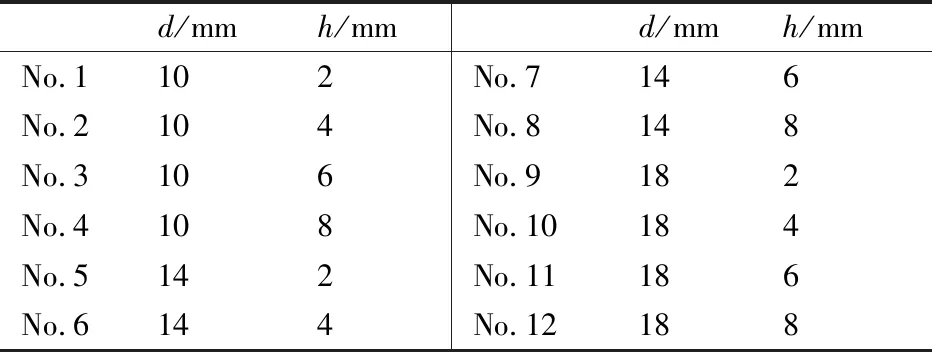
d/mmh/mmd/mmh/mmNo.1102No.7146No.2104No.8148No.3106No.9182No.4108No.10184No.5142No.11186No.6144No.12188

扇形擾流片的幾何模型如圖8所示。扇環形對應的弧心角為90°。扇形擾流片底部圓弧和頂部圓弧半徑相同，頂部圓弧圓心到扇形頂點的距離l為設計參數，通過改變l獲得不同形狀的擾流片。數值模擬狀態見表2。

邊界條件設置如圖9所示，噴管入口燃氣假設為理想可壓縮氣體，入口邊界條件為壓力入口，總壓p0=7.2 MPa，總溫T0=2.2×103K；噴管壁面為絕熱無滑移壁面；遠場邊界條件為壓力遠場，外流來流馬赫數Ma∞=2.96，環境大氣壓p∞=101 325 Pa，環境溫度T∞=300 K。

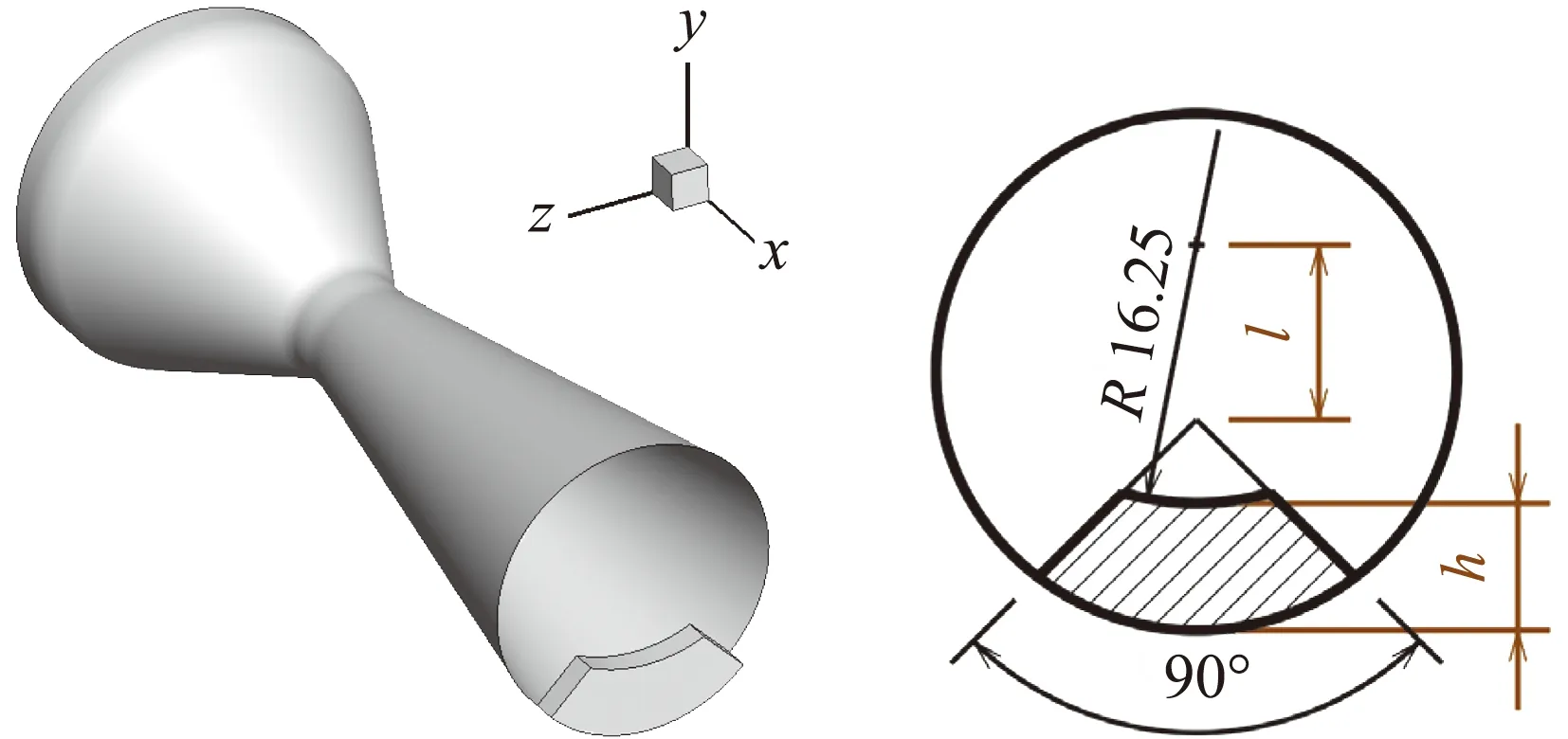
圖8 扇形擾流片幾何模型(單位: mm)Fig.8 Sector spoiler (unit: mm)

l/mmh/mml/mmh/mmNo.162No.788No.264No.8102No.366No.9104No.482No.10106No.584No.11108No.686No.121010

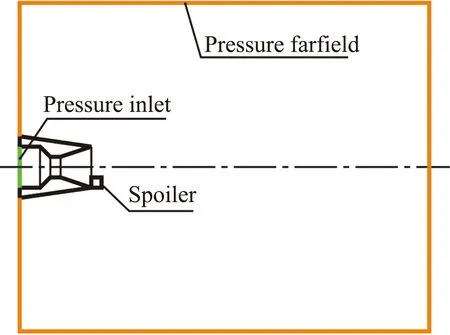
圖9 邊界條件Fig.9 Boundary conditions

3 計算結果分析

3.1 圓形擾流片

圓形擾流片上游噴管壁面靜壓分布如圖10所示。壁面靜壓在邊界層分離點受激波邊界層干擾的作用發生躍升，然后在主流的膨脹作用下逐漸下降，最后由于擾流片頂部弓形激波的作用再次上升。

噴管對稱面馬赫數云圖如圖11所示，選取h=4 mm、6 mm、8 mm三個狀態進行對比。由于擾流片阻礙了流體的流動，在擾流片上游出現了邊界層分離，并在分離點誘導出了一道斜激波，分離區的高壓在噴管擴散段壁面上的積分量就是擾流片式推力矢量裝置側向控制力的來源。同時在擾流片頂部有一道弓形激波，使位于激波后的擾流片迎風面存在高壓區，使擾流片受到了與噴管推力方向相反的作用力，從而引起了噴管的推力損失。隨著插入高度的增加，擾流片對噴流的阻礙作用增強，邊界層分離點前移，同時擾流片頂部弓形激波的強度增加。

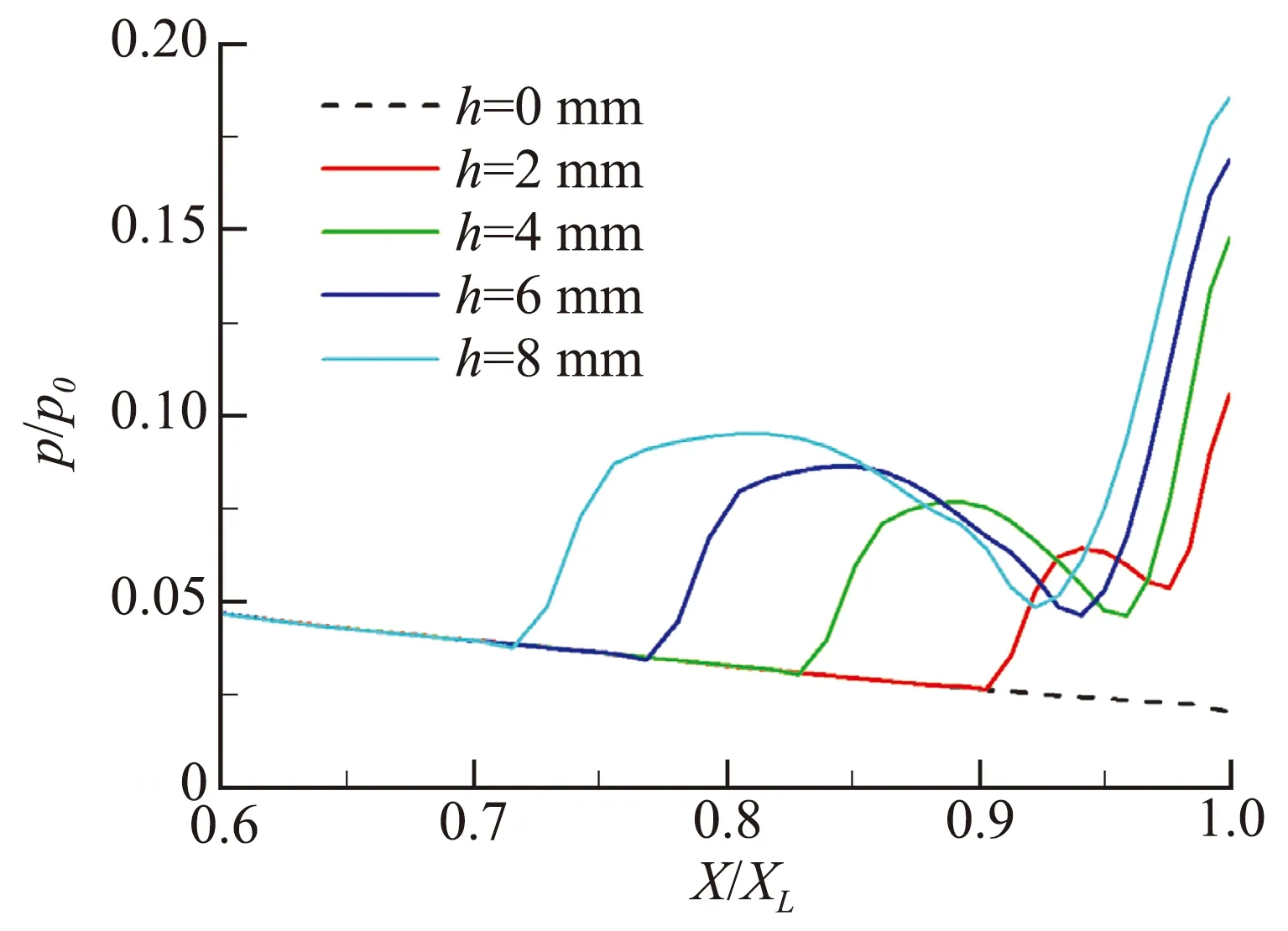
圖10 噴管壁面靜壓分布Fig.10 Pressure distribution at the nozzle wall

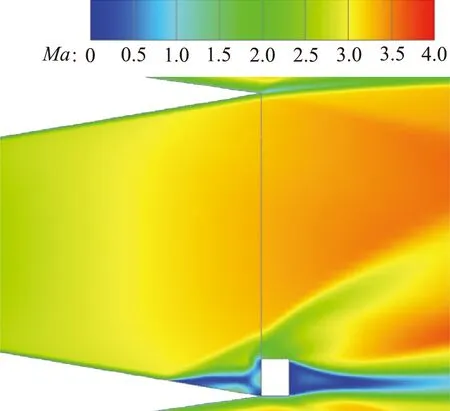
(a) h=4 mm

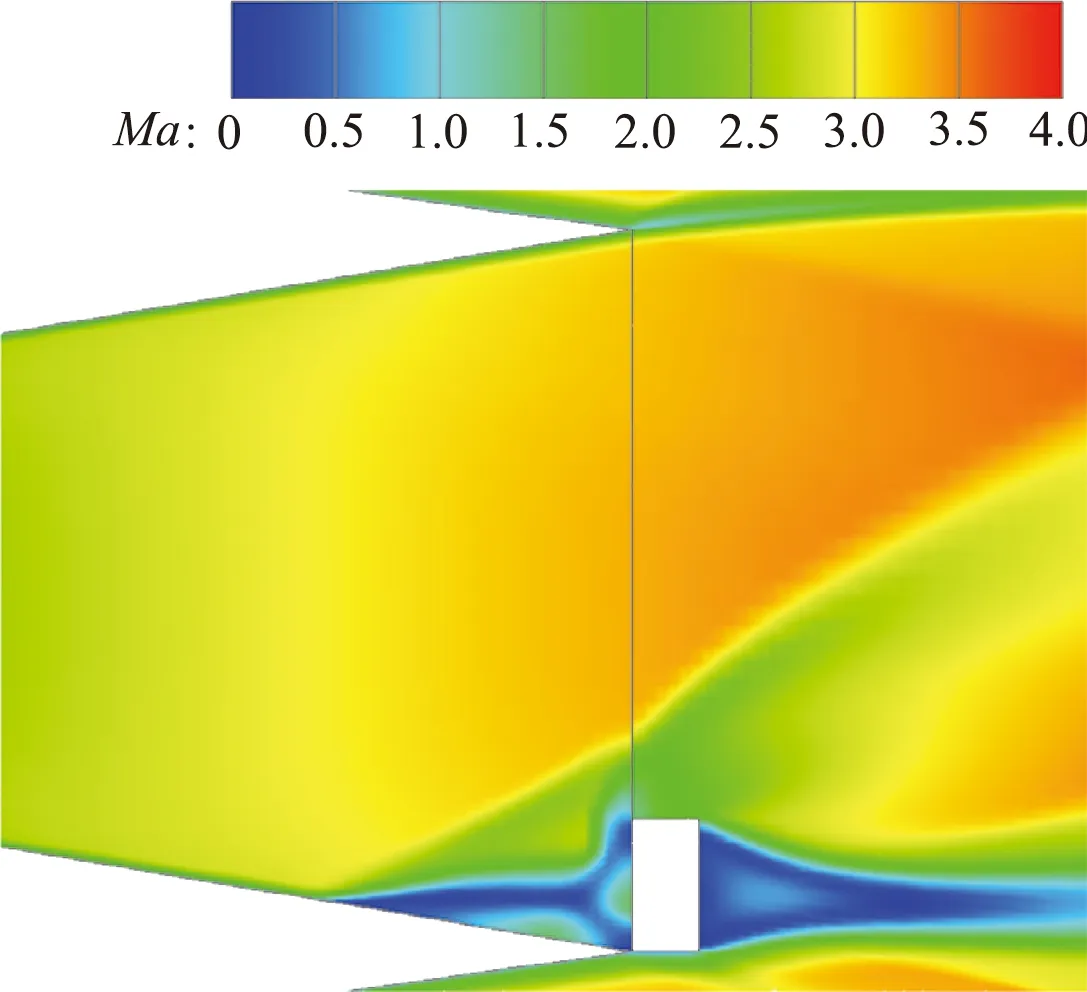
(b) h=6 mm

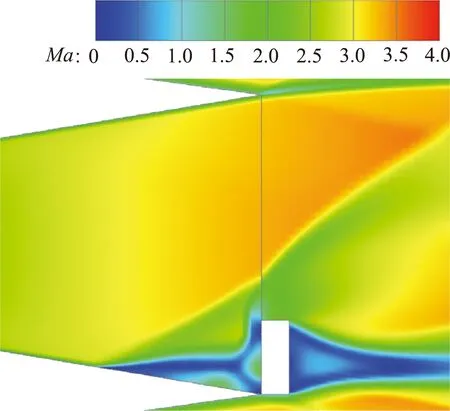
(c) h=8 mm

圖12給出了圓形擾流片產生的推力矢量角及推力損失隨插入高度的變化曲線。推力矢量角與推力損失都隨著擾流片插入高度的增加而增加，但呈非線性關系。這是由于擾流片形狀為圓形，其堵塞噴管的有效面積隨插入高度增加而呈非線性增長。

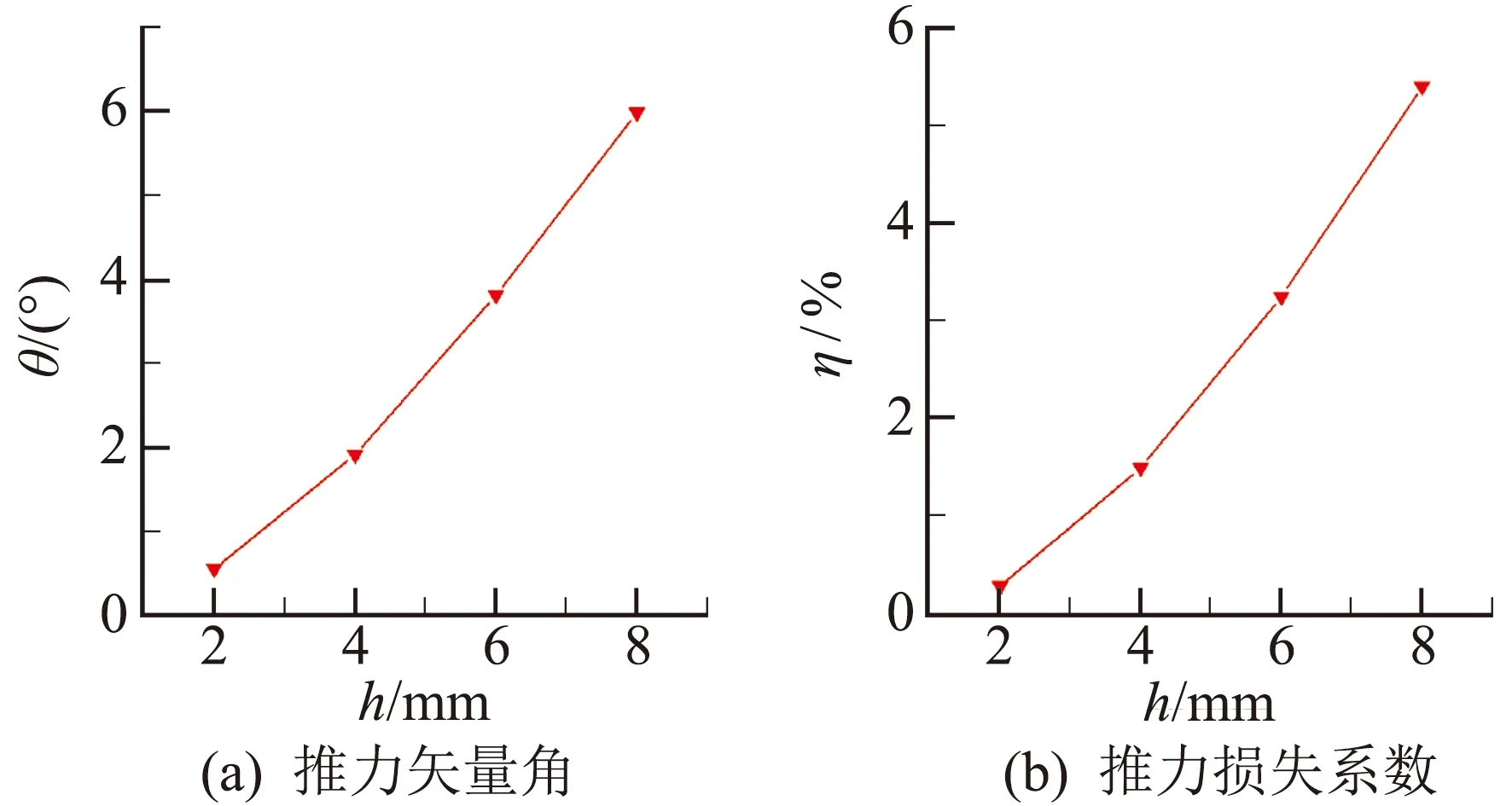
圖12 圓形擾流片推力矢量特性曲線Fig.12 Thrust vector performance of round spoiler

3.2 弧頂矩形擾流片

圖13給出了三組插入高度相同但寬度不同的弧頂矩形擾流片上游噴管壁面靜壓分布對比曲線圖。在擾流片插入高度相同的情況下，擾流片越寬，邊界層分離點就越靠前。這是由于隨著擾流片變寬，其堵塞噴管的有效面積增大，使擾流片上游的逆壓梯度增高。同時，隨著擾流片變寬，噴管出口處壁面壓力的峰值逐漸降低。這是由于分離點前移，分離區范圍越大，擾流片頂部距離主流區越遠，而擾流片頂部弓形激波強度越低。

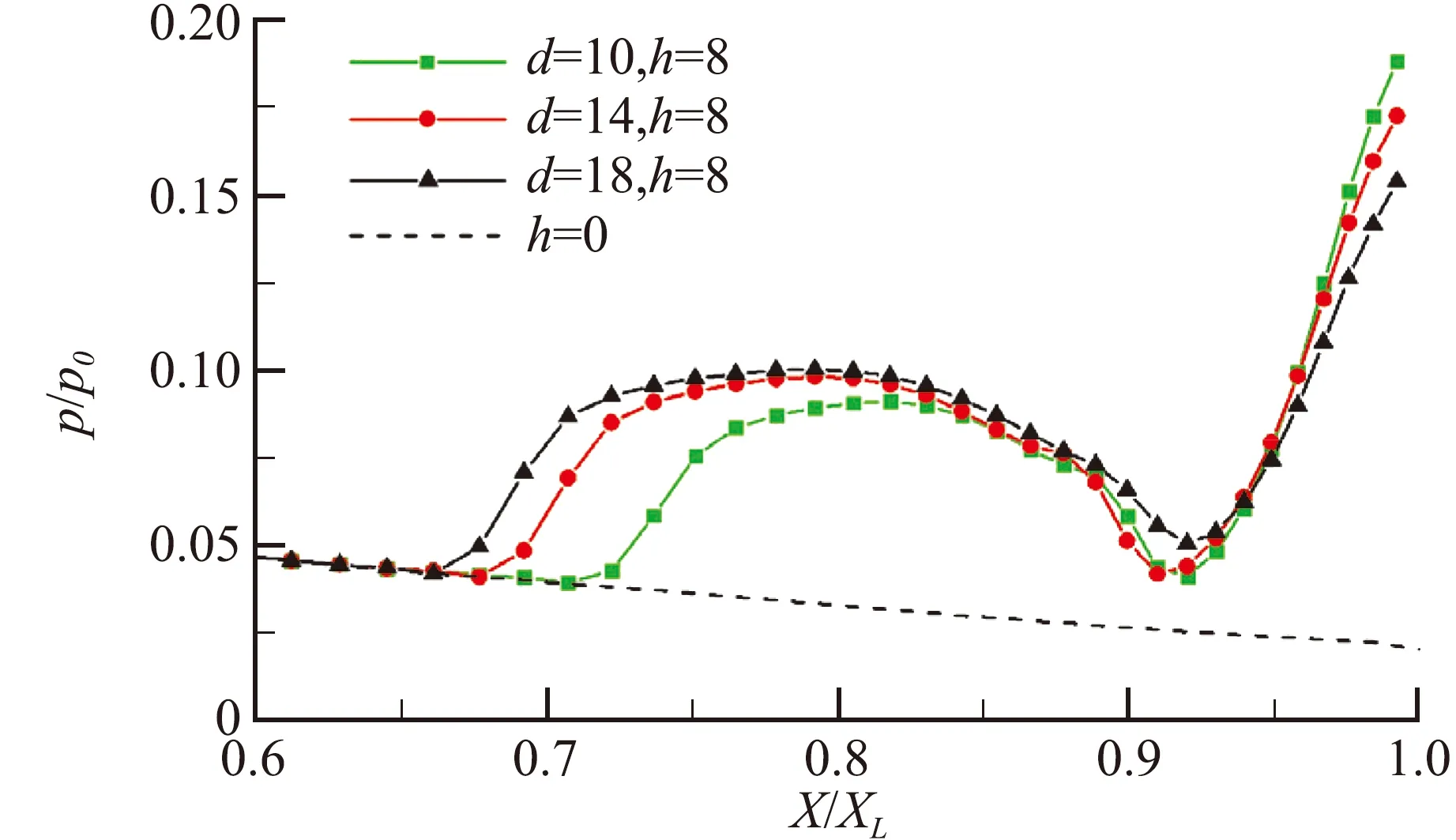
圖13 弧頂矩形擾流片上游噴管壁面靜壓分布Fig.13 Pressure distribution at the nozzle wall

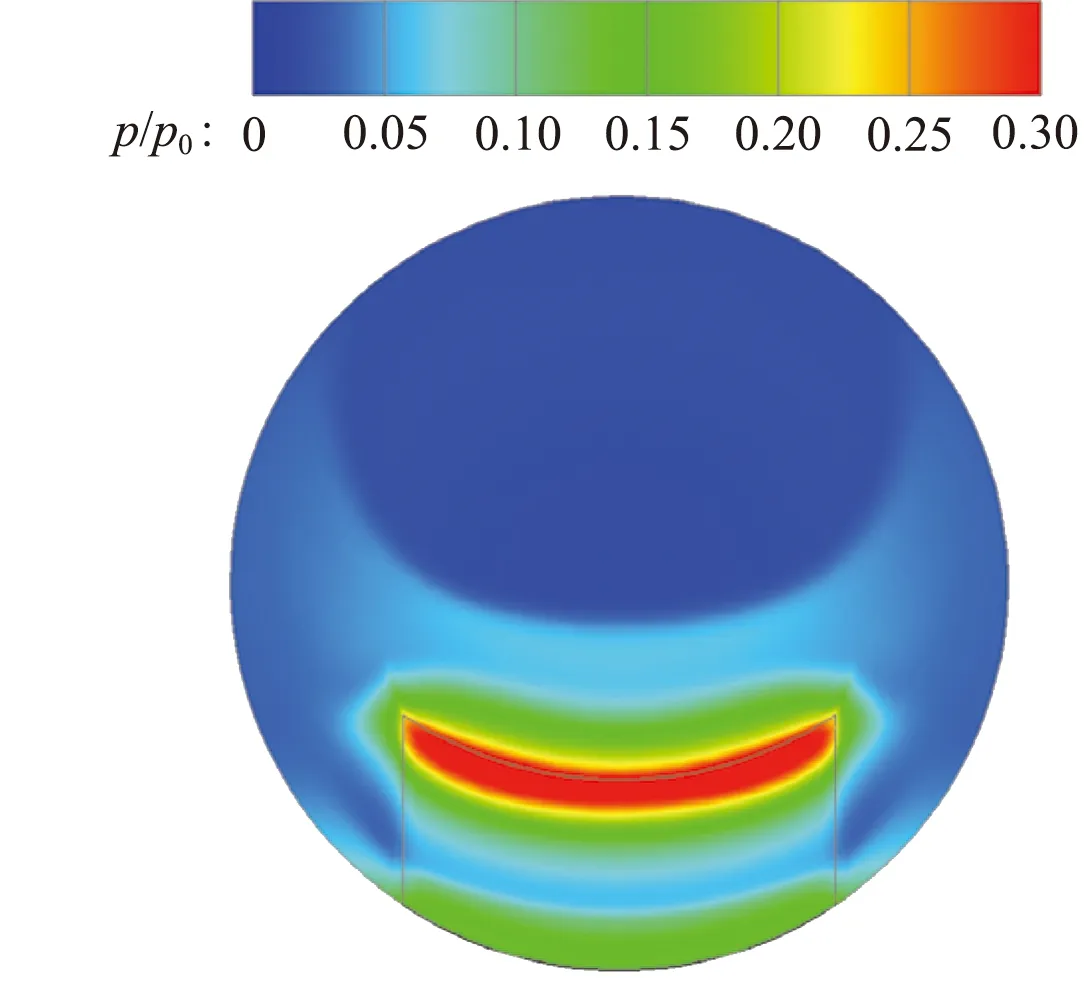
噴管出口截面靜壓分布如圖14所示。擾流片迎風面頂部由于斜激波及弓形激波后氣流的作用而產生一個高壓區，即圖中紅色區域。隨著擾流片寬度增加，頂部高壓區的周向(寬度方向)范圍增加，而徑向(高度方向)范圍減小，故高壓區面積隨擾流片寬度變化較小。由于擾流片高壓區是產生推力損失的主要原因，推力損失的值與高壓區面積相關，因而可以推斷推力損失隨擾流片寬度變化較小。

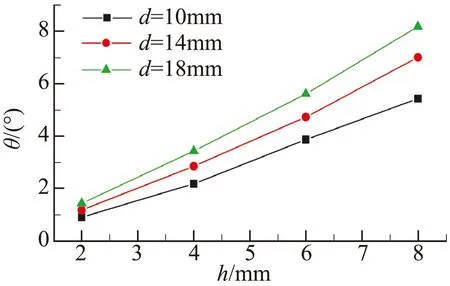
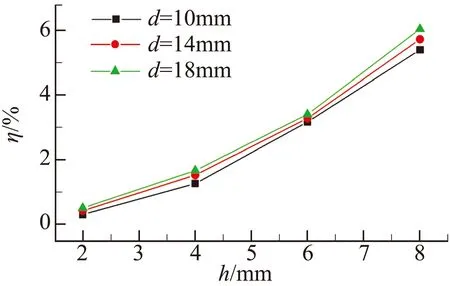
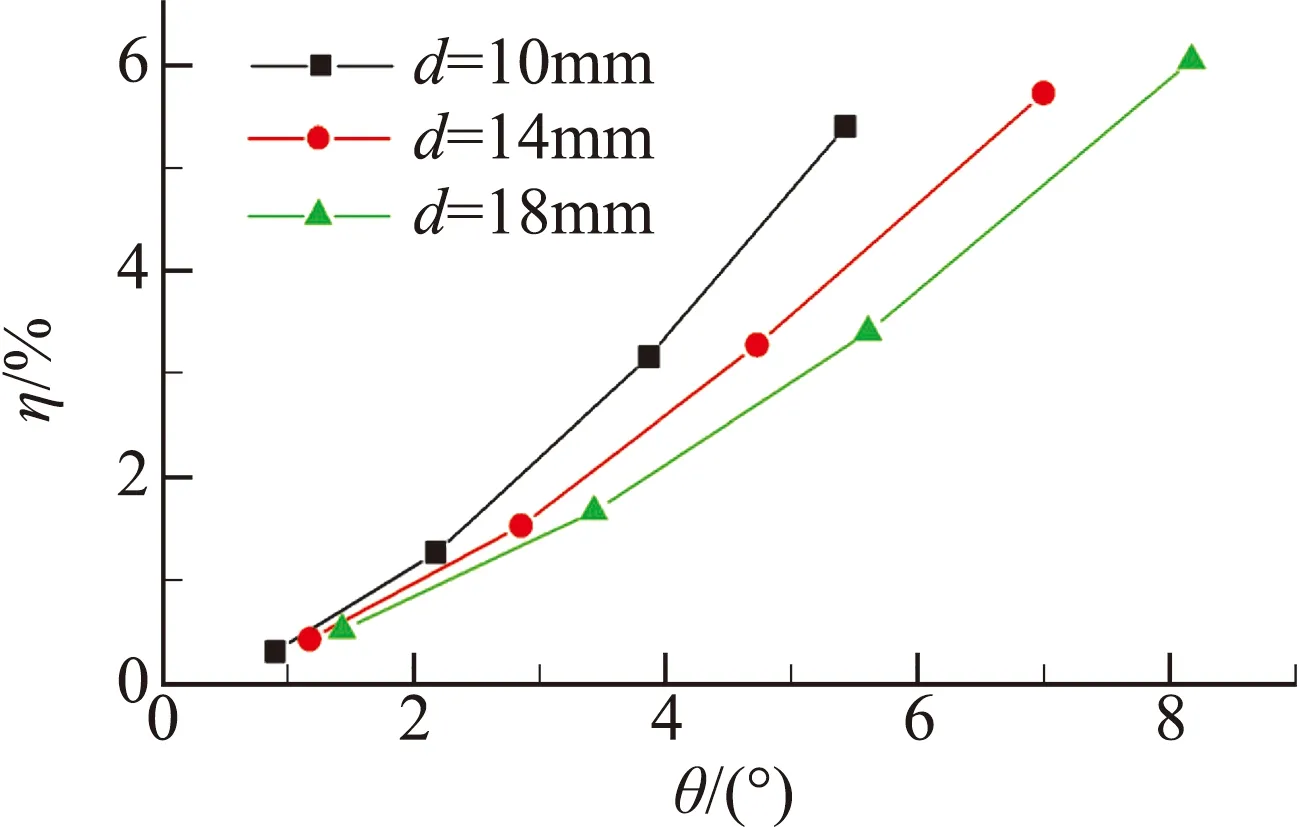
圖15給出了三組不同寬度的弧頂矩形擾流片的推力矢量特性曲線。由圖15(a)可知，隨擾流片插入高度增加，推力矢量角增大。而在插入高度一定時，隨著擾流片寬度增加，推力矢量角也隨之增大。因而對于弧頂矩形擾流片而言，推力矢量角受擾流片高度及寬度的共同影響。而由圖15(b)可知，推力損失系數對擾流片寬度變化不敏感，其大小主要取決于擾流片插入高度。由圖15(c)可知，在產生的推力矢量角相同時，越寬的擾流片產生的推力損失越小，其中d=18 mm的弧頂矩形擾流片推力損失最小。對于同樣產生推力矢量角約為5.5°的工況，增大擾流片寬度可以使推力損失從5.4%降至3.4%。因此，對于矩形擾流片而言，可以通過增大擾流片寬度的方式減小推力損失，提高控制效率。

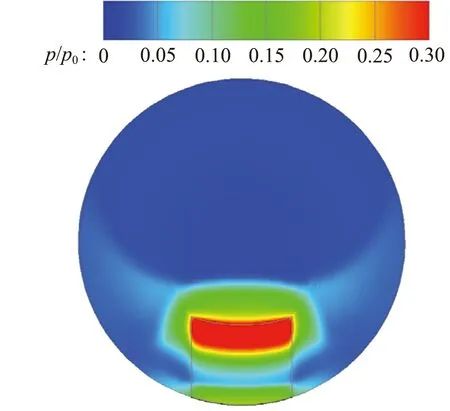
(a) d=10 mm，h=8 mm

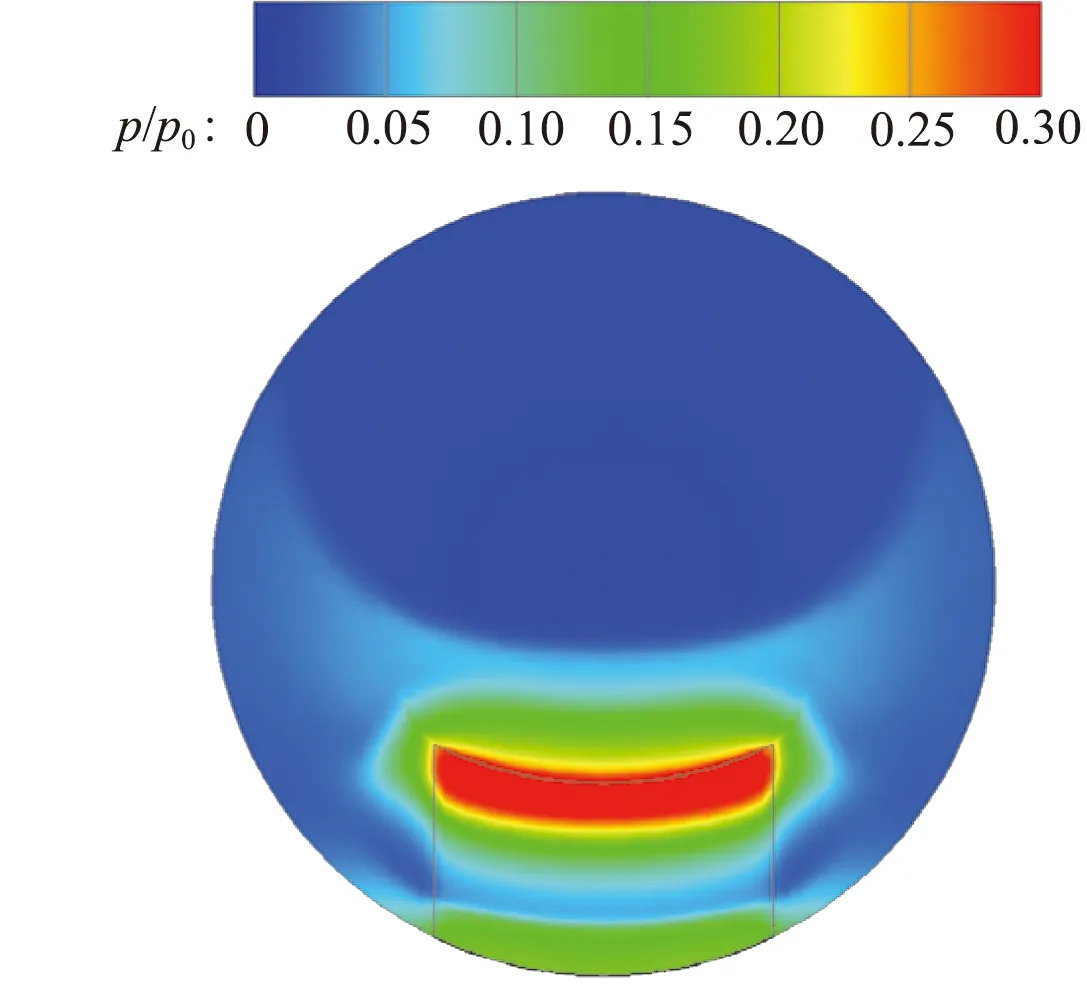
(b) d=14 mm，h=8 mm

(c) d=18 mm，h=8 mm

3.3 扇形擾流片

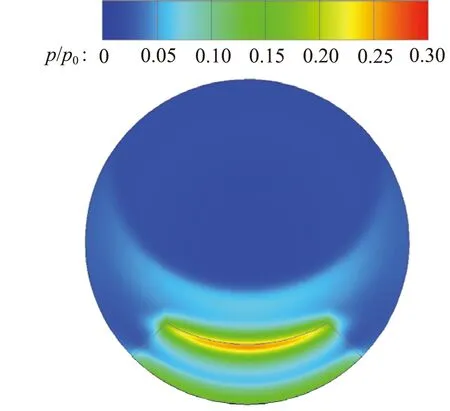
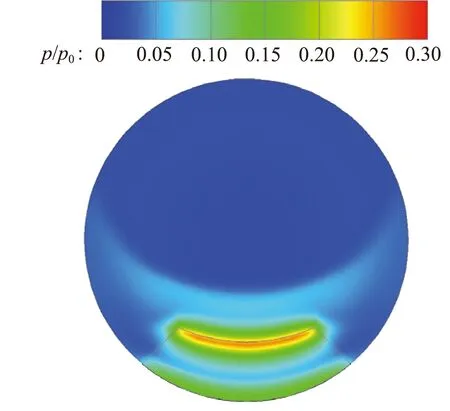
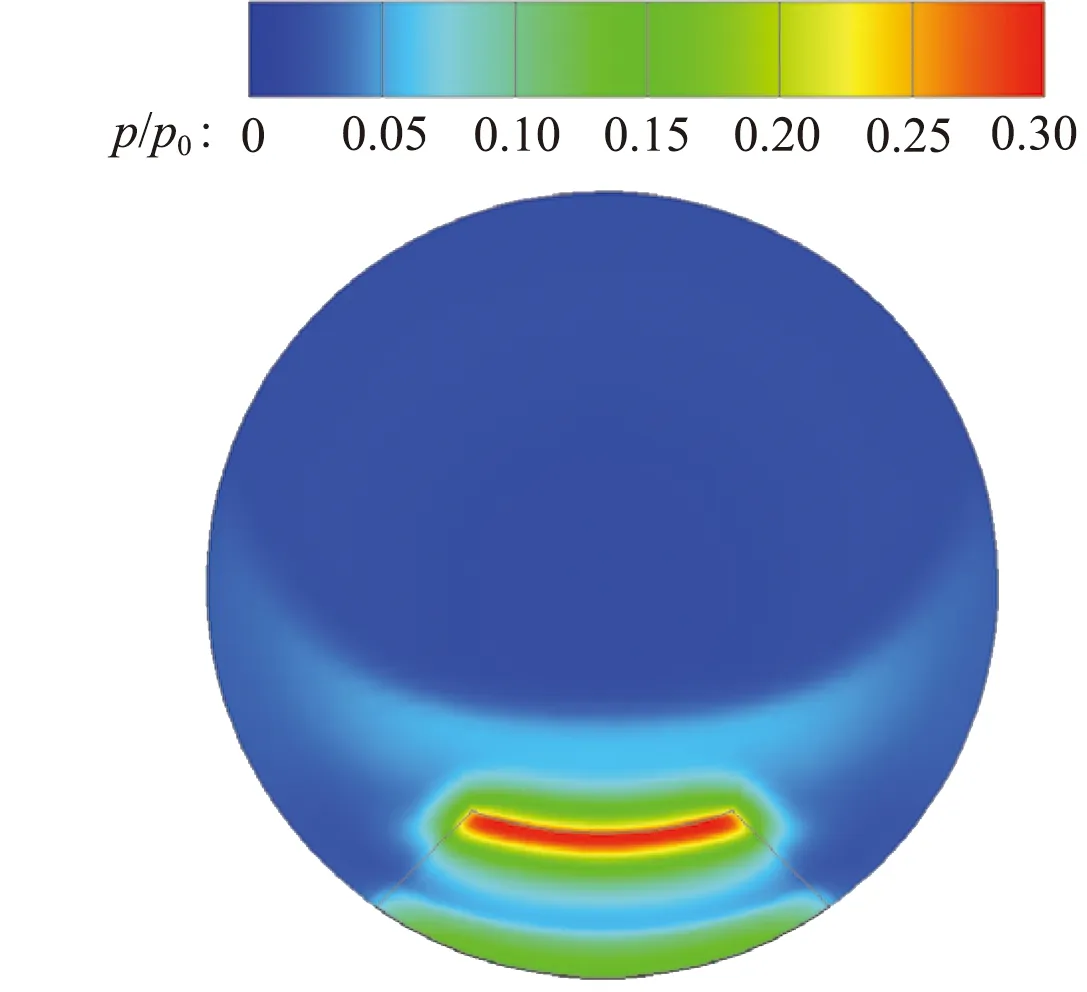
噴管出口截面靜壓分布如圖16所示。扇形擾流片在插入高度一定的前提下，隨著l的增加，頂部高壓區周向范圍減小，而徑向范圍增加，導致推力損失隨l變化較小。

圖17給出了不同l(頂部圓弧圓心到扇形頂點的距離)的三組扇形擾流片的推力矢量特性曲線。

由圖17(a)可知，在參數l一定時，推力矢量角隨擾流片插入高度增加而增加，而在擾流片插入高度一定時，推力矢量角隨參數l增加而減小。即推力矢量角受擾流片插入高度以及參數l的共同影響。

如圖17(b)所示，在插入高度一定時，推力損失隨參數l的變化非常小，說明推力損失主要取決于擾流片插入高度。結合前文中弧頂矩形擾流片相關結論進行分析，在插入高度一定時，無論是改變擾流片寬度還是改變參數l，都會直接改變擾流片面積。因而可以初步判定對于特定形狀的擾流片而言，在插入高度一定時，推力矢量角對擾流片面積變化較為敏感，而推力損失系數對擾流片面積的變化不敏感。

由圖17(c)可知，在推力矢量角相同時，參數l越小的擾流片產生的推力損失越小，其中l=6 mm的扇形擾流片推力損失最小。因而對于扇形擾流片，減小參數l可以減小推力損失，提高擾流片的控制效率。

3.4 三種擾流片對比

針對上述的圓形、弧頂矩形、扇形這三種擾流片，設計擾流片面積同為s=112 mm2，插入高度同為h=8 mm的三種外形，即：擾流片半徑為13.96 mm的圓形擾流片，寬度為14 mm的矩形擾流片，l=11.16 mm的扇形擾流片，并對其進行對比研究。

(a) 推力矢量角

(b) 推力損失系數

(c) 推力損失系數隨推力矢量角變化

圖15 弧頂矩形擾流片推力矢量特性曲線
Fig.15 Thrust vector performance of rectangle spoiler

(a) l=6 mm，h=6 mm

(b) l=8 mm，h=6 mm

(c) l=10 mm，h=6 mm

圖16 噴管出口截面靜壓分布
Fig.16 Pressure ratio profiles at nozzle outlet plane

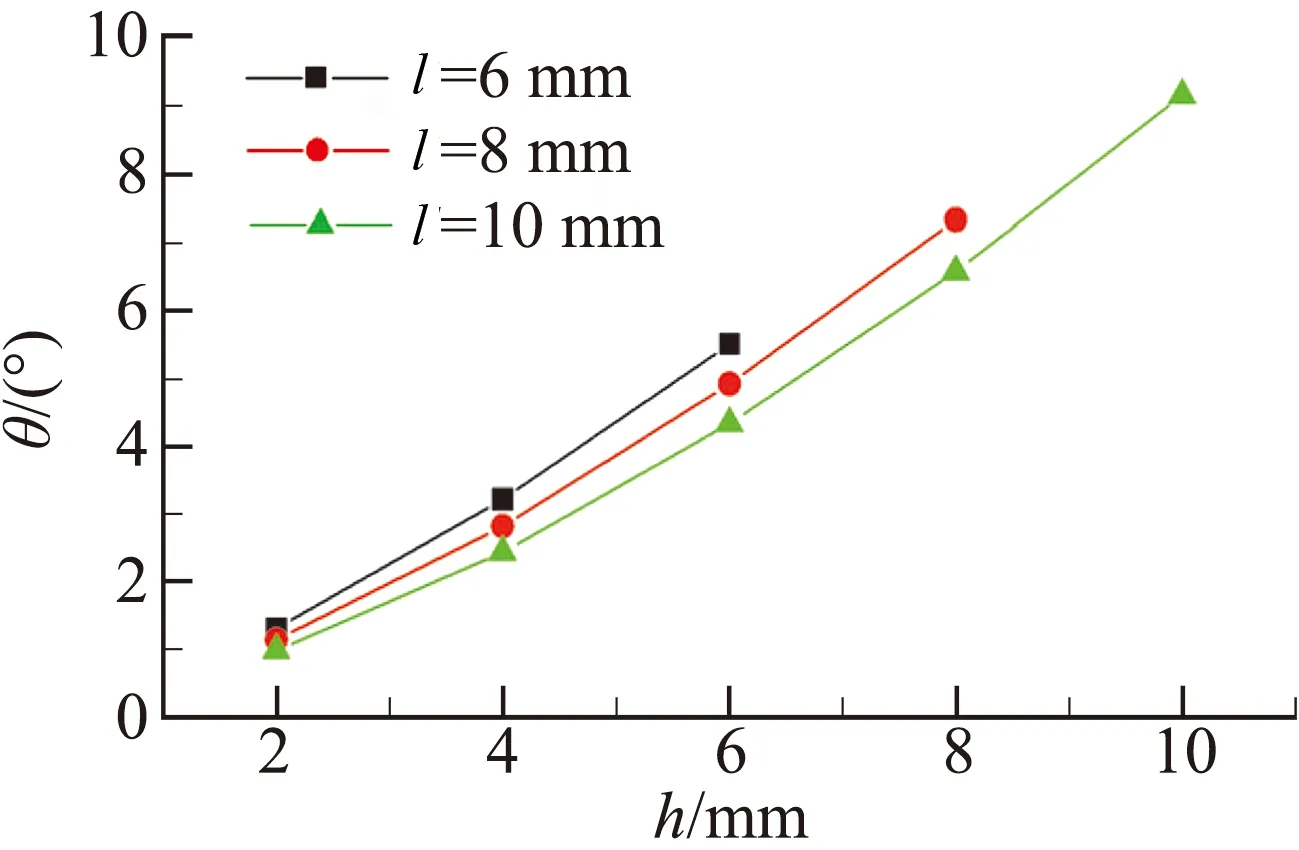
(a) 推力矢量角

圖17 扇形擾流片推力矢量特性曲線
Fig.17 Thrust vector performance of sector spoiler

噴管出口截面靜壓分布如圖18所示。由于幾何外形不同，三種擾流片迎風面高壓區的形狀以及分布范圍都有較大區別。由于弧頂矩形擾流片頂部較寬，其頂部高壓區的周向范圍較大，扇形擾流片次之，圓形擾流片高壓區范圍最小。因而在面積相同的情況下，弧頂矩形擾流片產生的推力損失最大，扇形擾流片次之，圓形擾流片最小。

三種擾流片的推力矢量特性如圖19所示。由圖19(a)可知，在擾流片面積及插入高度相同時，弧頂矩形的推力矢量角最大，圓形擾流片推力矢量角最小；由圖19(b)可知，在擾流片面積及插入高度相同時，弧頂矩形的推力損失系數最大，圓形擾流片推力損失系數最小。因此，在擾流片面積及插入高度一定的前提下，幾何形狀對于推力矢量特性有一定影響。

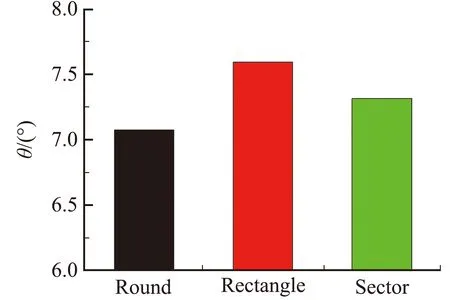
(a) 推力矢量角

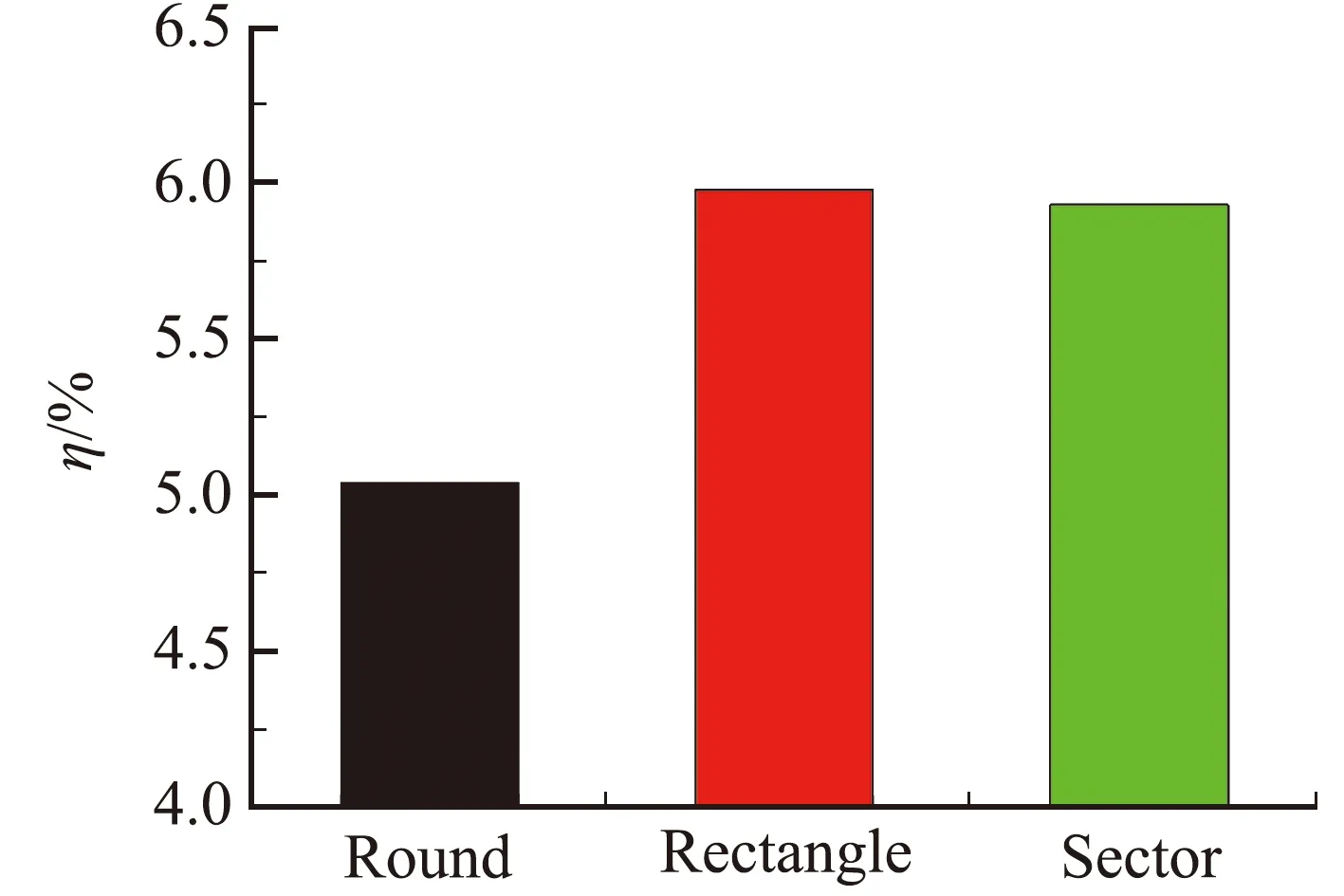
(b) 推力損失系數

4 結 論

本文將通過數值模擬手段，針對圓形、弧頂矩形以及扇形這三種擾流片外形，研究了擾流片幾何形狀對噴管推力矢量特性的影響規律。通過對數值模擬結果的分析，得出以下結論：

(1) 推力矢量角與推力損失系數都隨著擾流片插入高度的增加而增加。

(2) 斜激波和弓形激波后的氣流在擾流片迎風面頂部形成了高壓區，噴管推力損失的值與高壓區面積相關，而高壓區面積受擾流片形狀影響。

(3) 對于矩形擾流片，可以通過增加擾流片寬度的方式減小推力損失，提高控制效率，對于同樣產生推力矢量角約為5.5°的工況，增大擾流片寬度可以使推力損失從5.4%降至3.4%；對于扇形擾流片，可以通過減小上圓弧圓心與扇形頂點距離的方式減小推力損失，提高控制效率。

(4) 在擾流片插入高度及面積一定時，幾何形狀對推力矢量特性有一定影響，其中弧頂矩形擾流片的推力矢量角及推力損失均為最大，圓形擾流片均為最小。