抖動法篩選特征點仿真

李日亮， 徐 曉

(華南理工大學 物理與光電學院，廣東 廣州 510640)

0 引 言

在機器視覺領域中，雙目三維重建方法多數采用提取圖像特征點進行特征匹配[1,2]，通過匹配點來計算出其對應的空間三維坐標[3,4]，而特征匹配的方法涉及到的都是二維圖像。由于雙目視差[5,6]的存在，雙目圖像并不相同，只是相似，對應點鄰域的圖像是有差異的。這種差異引起對應點匹配不準，或者找錯匹配點而產生誤匹配，從而使計算出的三維坐標不準確或者計算出不存在的點[7,8]。大量的實驗和理論表明，只要從不同的方位采集圖像，在三維物體光照情況固定，并且光照條件足夠體現出物體形貌信息的情況下，是可以避免上面的誤匹配問題的[9～12]。

但在真實工況下，被攝物體保持穩定姿態和光照穩定的時間都是有限的；同時考慮到成本，也不會用多相機和硬件復雜的數據處理系統。項目組要設計一個雙目三維重建系統，相機由平移臺控制，可相對物體運動，并要求在盡量短的時間內，使相機相對物體移動盡量短的距離和少的次數采集新圖像，并補充更多的新的目標物三維信息。考慮到相機移動以尋求不同拍攝角度時[12,13]，兩相機間相對關系若不固定，也會為結果計算和系統標定帶來復雜性，并會降低檢測復原的精度[14～16]，所以，相機移動是沿精確的已知軌道。在一定精度條件下，是工程可實現的。命名該方法為抖動法[17]，仿真實驗驗證了本文算法的有效性。

1 抖動法三維復原系統與仿真典型條件

抖動法三維復原系統示意圖如圖1。系統有2個相機，通過移動平臺控制使兩相機位置發生變動[18]。

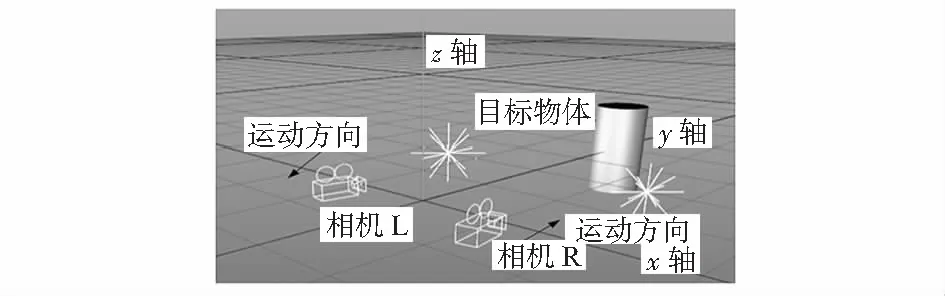
圖1 抖動法三維復原系統

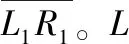
為驗證抖動法，仿真僅移動相機1～2次。通過仿真發現，如果相機沿基線運動，不能獲得太多的驗證信息。而項目組分析發現，極幾何條件要求特征點匹配時，左右圖像β要一樣，移動方向要顯著改變雙目成像極幾何條件中的β取法，才能對最先的三維復原點有明顯的檢驗效果。

為了運動的典型性和坐標易算性，作為典型條件，讓兩相機分別沿著垂直L1R1方向移動。同時，鑒于旋轉并不能改變明顯改變β取法，也不引入相機旋轉。

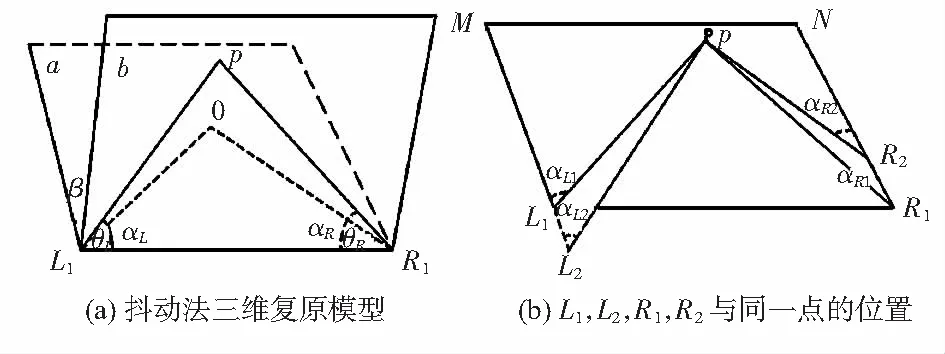
圖2 算法仿真模型

2 抖動算法仿真

2.1 左相機兩圖片的匹配和右相機圖片匹配

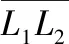
類似左相機，右相機有R1-R2系統。其中，∠PR1R2為αR1，∠PR2N為αR2(αR1>0，αR2>0),R1R2垂直于L1R1。R1，R2處相機圖像的匹配與左相機處理方式相同。

2.2 三個直角坐標系統

為計算直角坐標，抖動法三維重建模型有3個直角坐標系統。圖3(a)為這三個直角坐標系統。L1-R1系統中，以L1為原點，L1R1為x軸，L1M為y軸。L1-L2系統中，以L2相機光心為原點，L2L1為x軸，L2Q為y軸。R1-R2系統中，以R1相機的光心為原點,R1R2方向為x軸,R1L1方向為y軸。三個坐標系統都以垂直于基準極平面向上為z軸。

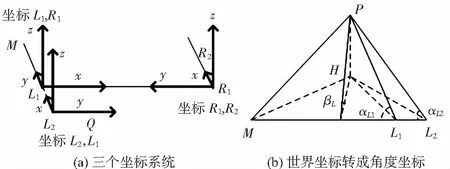
圖3 坐標轉換

設空間一點P在L1-R1系統的坐標為(xp,yp,zp)，在L1-L2系統的坐標為(xL,yL,zL),在R1-R2系統的坐標為(xR,yR,zR);轉換關系如下

(1)

如圖3(b)，在L1-L2系統中，面PML2與面HML2的夾角為，∠PL1M=αL1，∠PL2M=αL2；P點坐標是(xL,yL,zL)；世界坐標轉換成角度坐標如下

(2)

式中αL1，αL2的范圍為(0°,180°)。

2.3 抖動算法的流程

本文的實驗步驟如下：

1)圖像L1，R1坐標轉換，匹配，計算匹配特征點對的三維歐氏坐標(xp,yp,zp)[19]；

2)將三維復原的空間域坐標轉換成L1-L2系統的角度坐標，用圖像L1,L2的角度坐標匹配點檢查L1,R1轉換而來的角度坐標是否存在誤匹配點，如果有，則淘汰；

3)將剩余點復原到L1-R1系統空間域，再把空間域坐標轉換成R1-R2系統的角度坐標；

4)用圖像R1,R2的角度坐標匹配點檢查圖像L1,R1轉換而來的角度坐標是否存在誤匹配點，如果有，則淘汰;

5)用剩余點進行三維重建。

2.4 誤匹配點淘汰過程

由圖像L1,R1三維復原特征點的歐氏坐標(xp,yp,zp)，先轉成L1-L2系統的歐氏坐標(xL,yL,zL)，再通過式(2)，轉換成了L1-L2系統的角度坐標，記為(αL1P,αL2P,βLP)。L1,L2圖像直接匹配，得到匹配點的角度坐標為(αL1,αL2,βL)；以{(αL1,αL2,βL)}特征點集合為標準，來檢查{(αL1P,αL2P,βLP)}集合中是否有誤匹配點。

如圖4所示，表明了取某個βL時，且βLP≈βL時，兩類特征點的相互關系。其中，點表示集合{(αL1,αL2,βL)}中的點，圓圈表示{(αL1P,αL2P,βLP)}集合中的點。

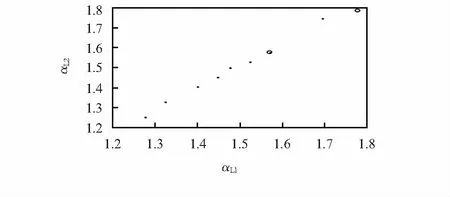
圖4 兩集合內點的關系

觀察圖4，{(αL1P,αL2P,βLP)}集合中的點，可以分為三類：a.離{(αL1,αL2,βL)}中某個點較近；b.離{(αL1,αL2,βL)}所有點較遠，但其橫坐標離某個點近；c.橫縱坐標都遠離{(αL1,αL2,βL)}的點。

a類點的劃分標準，是其距{(αL1,αL2,βL)}離中最近點的距離小于事先給定的閾值，這類點會被保留；b類點的劃分標準，是其橫坐標與{(αL1,αL2,βL)}中的某個點橫坐標的差的絕對值小于某個給定閾值，但其縱坐標與對應點的縱坐標的差距大于某個閾值，這類點會被拋棄；c類點就是除a，b類以外的點，其如何取舍，取決于這個點在L1和L2圖上對應位置的灰度值和灰度值沿αL方向一階導相互之間的差距，如果差距大于某個值，則此點被拋棄，否則，被保留。

2.5 三維復原

圖像L1,R1經淘汰后留下來的點，可用作三維復原。

3 實驗與探討

3.1 實驗一

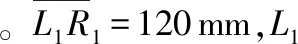
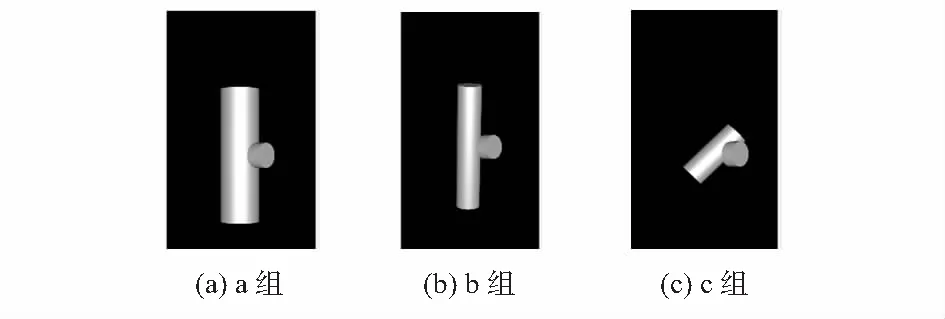
圖5 實驗組合圓柱

淘汰條件的設置如下：

1)判斷待淘汰點αL1軸0.02°范圍內有沒有參考點，如果有，繼續判斷待淘汰點αL2軸0.02°范圍內有沒有參考點，如果有，則保留該點；

2)判斷待淘汰點的αL1軸0.01°范圍內有沒有參考點，如果有，繼續判斷該參考點沿αL2軸方向與該待淘汰點差值絕對值是不是大于0.02°，如果是，則淘汰該點；

3)判斷待淘汰點的αL1軸0.02°范圍內有沒有參考點，如果沒有，判斷待淘汰點的αL2軸0.02°范圍內有沒有參考點，如果沒有，則繼續判斷該點在L1和L2圖上的灰度值差值絕對值是否小于30，灰度值一階導差值絕對值是否小于10。如果同時滿足兩個條件則留下該點。如圖4所示。

把組合圓柱體還原在L1-R1系統歐氏坐標中，將三維重建結果以“*”的形式打到同一張圖上。將組合圓柱體和淘汰后三維復原結果畫在另一張圖上，如圖6所示。同一行β,匹配錯誤一個點導致的深度方向誤差[6]為3.4 mm。取圓柱面附近一個像素點距離內為正確匹配點，由于本次實驗2個圓柱距離很近，故而取圓柱頂面和底面高度各加減3 mm內：離圓心距離在(r(半徑)+3)mm以內為正確匹配點;圓柱底面高度加3 mm到頂面高度減3 mm范圍內：距離圓柱圓心的距離在[r-3:r+2.25]mm范圍內為正確匹配點。統計數據如表1所示。

表1 a,b,c組圓柱過濾前后正確匹配點

a組圓柱嚴格匹配三維重建結果如圖6。

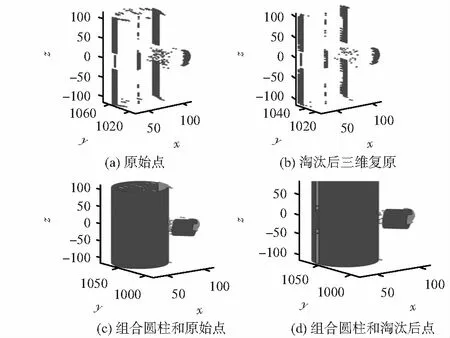
圖6 a組圓柱三維重建結果

將淘汰前正確率設為x,淘汰后正確率設為y，它們之間關系如圖7(a)所示，小方塊表示a組圓柱數據，*號表示b組圓柱數據，小圓圈表示c組圓柱數據。正確率提高量(y-x)/x×100 %與x的關系如圖7(b)所示。

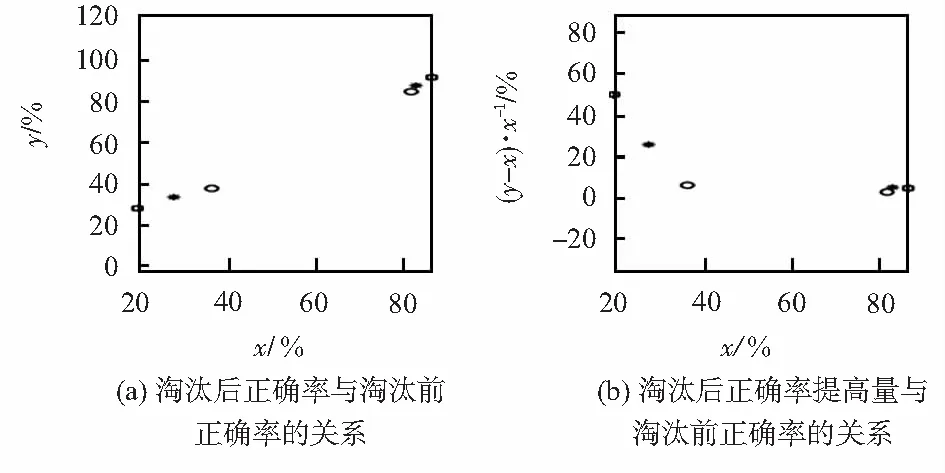
圖7 正確率統計

3.2 實驗二

實驗二的目的，將一個對讀者有印象的形狀較復雜的對象作為目標物，來直觀上檢查方法的有效性。本實驗采用3D仿真軟件Cinema 4D模擬相機拍攝藝術家頭像雕塑，放置L1，L2，R1，R2共4個相機在4個不同的位置模擬拍照，得到4張1 628×1 236的圖像。L1(到L2)，R1(到R2)的移動距離為20 mm。其他實驗參數設置與實驗一相同[19]。

圖像L1，R1三維重建結果如圖8(c)所示。淘汰條件設置與實驗一相同。

圖8 原始圖像與過濾前后的三維重建結果

由圖8可以看出，淘汰后人側臉有明顯改善。

4 結 論

實驗一表明：三維重建點云經過淘汰后正確點的比例會提高，證明了實驗方法顯著淘汰錯誤點同時又保留足夠多的正確點。而且，原始匹配的誤匹配率越高，經過抖動過濾的改善情況越明顯。實驗二直觀地表明，在明顯改變β取值方向的情況下，左右相機抖動前后的匹配結果能夠減小傳統三維重建的不確定度，改善三維重建的結果。

仿真實驗驗證了抖動算法篩選特征點的有效性。改善率和正確率的函變關系的確定，為未來抖動法三維重建的運動步長以及運動次數提供參照，為抖動法的工程設計和實現，打下了基礎。