朱永波， 盧國梁

(1.山東大學 機械工程學院，山東 濟南 250061; 2.山東高效潔凈機械制造教育部重點實驗室，山東 濟南 250061)

0 引 言

現代科學技術正向微型化、精密化快速發展，微、納米技術甚至被譽為十大可改變世界的科技之一[1]。微動平臺作為微納米技術中的一個重要執行元件，廣泛應用于微裝配、細胞注射、微操作等[2～5]，其輸出位移的檢測技術作為微納操控精度的關鍵，得到越來越多的研究。目前采用光柵和激光尺[6,7]對安裝位置要求十分嚴格，容易被遮擋等特點導致其往往難以應用于多自由度微動系統中；另一方面，對于微裝配合、細胞操作等一些需要可視化操作的場合下，光柵和激光尺也難以滿足測量要求。

基于計算機視覺的測量方法以其高精度、可視化、可適用于多自由度系統測量等特點而成為研究熱點，越來越多的學者也進行了一些顯微視覺的測量研究。Davis C Q[8,9]、張憲民[10]和謝勇君[11]等人結合計算機視覺及頻閃成像測量微運動，但圖像處理算法時間復雜度較高，難以滿足實時測量要求；Clark L[12]和陳文海等人[13]利用圖像邊緣特征配準計算微動平臺輸出位移，方法簡單，但精度相對較低；黃贊等人[1]利用單演曲率張量與數字圖像相關法測量微位移，魯棒性較好，可實現亞像素級精度，但算法較為復雜，難以實現實時測量。

針對以上問題，本文提出了一種基于計算機顯微視覺的微動平臺測量方法。并通過實驗驗證，證明了該方法具有測量精度高、效率高、可視化、成本低以及適合多自由度微動平臺測量的特性。

1 微動系統與成像模型

本文所述基于橋式放大機構的微動平臺如圖1所示[14]，其主要由基于三角放大原理的橋式放大機構和平行四邊形導向機構組成。工作時，壓電換能器(piezoelectric transducer,PZT)驅動橋式放大機構，使得微動平臺輸出部分在平行四邊形導向機構作用下沿x軸方向運動，其行程可達數十微米(μm)。

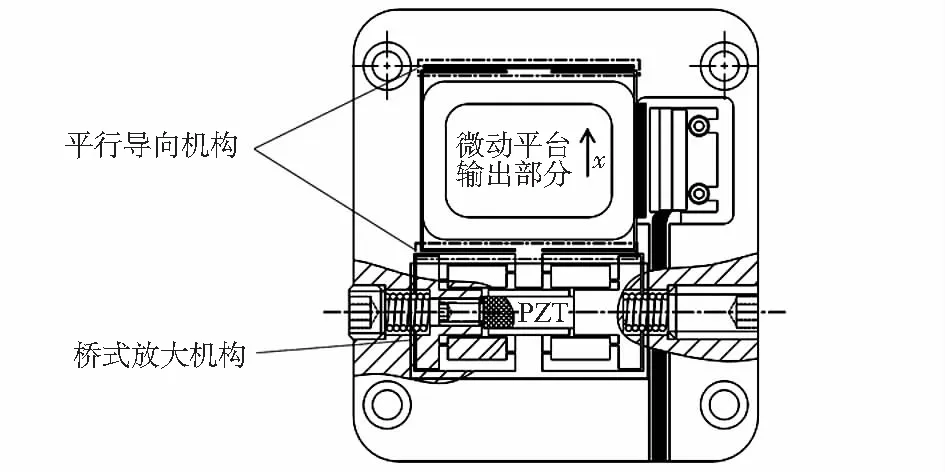
圖1 微動平臺

為測量微動平臺輸出位移，本文設計了顯微視覺系統。該系統由CCD相機、顯微鏡(放大倍數×5～50)、微動平臺、標記物(硅基鍍金膜)以及一臺計算機(Intel Core i3—4170 CPU 3.7 GHz 4 GB RAM)組成。系統成像模型可簡化為一針孔模型[15]，其成像關系如圖2，根據圖2，圖像坐標系和固連于微動平臺的坐標系變換關系為

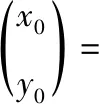
(1)

式中θ為Oximg和O0x0的夾角；c1，c2為原點O′到O0的平移關系。對于本文中的單自由度系統，式(1)可簡化成

x0=kximgcosθ+kyimgsinθ+kc1

(2)

式中k，θ及c1均可由相機標定獲得。

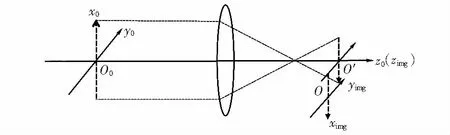
圖2 小孔成像模型

2 基于二值化圖像的重心的位置計算

2.1 二值化處理

標記物在微視覺成像系統中成像如圖3(a)，通過圖3(b)其灰度直方圖可以看出，其灰度值分布主要集中在2個區間，基于此特點，對灰度圖像進行二值化處理

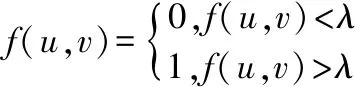
(3)

式中λ為閾值，其由Ostu法[16]確定。

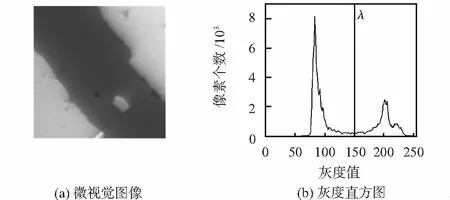
圖3 微視覺圖像及其灰度直方圖

2.2 濾波與連通域提取

由于噪聲等影響，二值化后的圖像在連通域內存在一些“小孔”以及“間隙”，進行形態學濾波處理

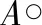
(4)

Xk=(Xk-1⊕B)∩A,k=1,2,3,…

(5)

式中 當Xk=Xk-1時停止迭代，此時Y=Xk，連通域提取完成。同時，剔除面積小于特定閾值的連通域以消除噪聲影響。

2.3 重心位置計算

如圖4(b)，經過濾波后的圖像由3個連通域組成，其中連通域3在整個微動平臺運動過程中一直在視場內，因此，可以追蹤連通域3的重心坐標位置，計算微動平臺輸出位移。重心位置計算公式如下

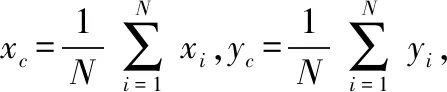
(6)

式中Y3為連通域3，將式(6)獲得的重心坐標代入式(2)中，可求得微動平臺輸出位移。

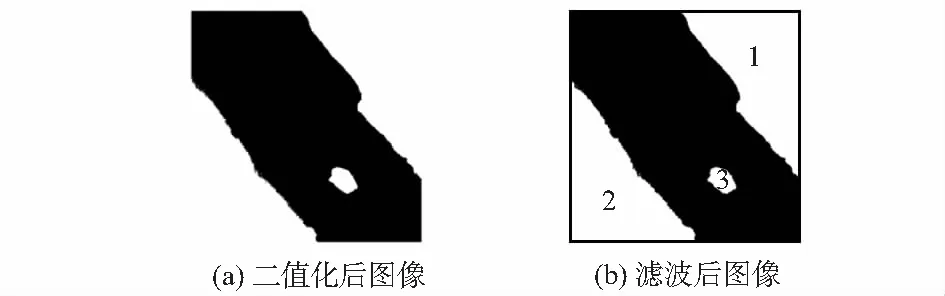
圖4 二值化及其閉合運算后圖像

3 實驗驗證

為驗證本文方法的有效性，對微動平臺進行了測量實驗，并對比了基于圖像塊匹配算法[17]的位移測量。實驗中，以累積均方誤差(mean square error,MSE)評價各測量方法的精度

(7)

式中xi,ref為由光柵尺測量得到的第i個采樣點數據，由于光柵分辨率(1 nm)遠高于顯微視覺的測量精度，因此，選取其作為實際位移量的參考值，xi為其他方法測量的位移值。

3.1 階躍信號與正弦信號測量誤差及效率

圖5為當微動平臺以階躍和正弦信號運動時，本文方法和圖像塊匹配方法的測量結果。

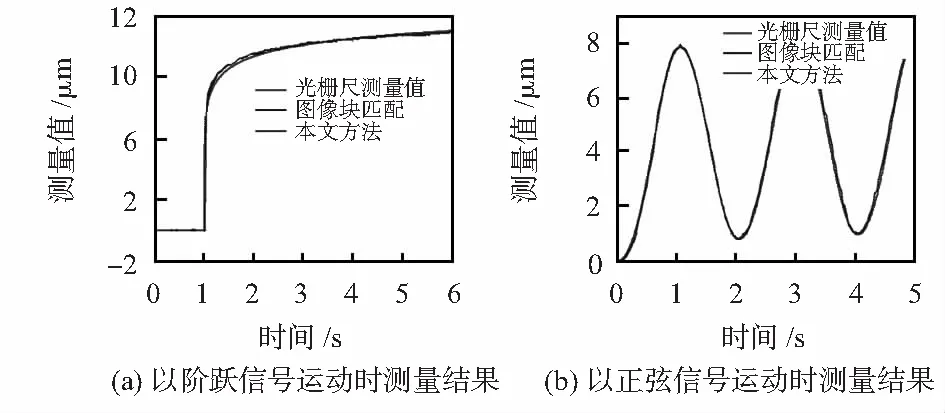
圖5 微動平臺沿不同信號運動時位移測量結果

當微動平臺以階躍信號方式移動時，基于圖像塊匹配算法的累積方誤差為0.142 μm，本文方法的累積均方誤差為0.163 μm；而當微動平臺以正弦信號移動時，基于圖像塊匹配算法的累積均方誤差為0.229 μm，本文方法的累積均方誤差為0.231 μm。兩種方法測量誤差比較接近，但本文方法每幀圖像處理時間約為4.19 ms，而基于圖像塊匹配的算法每幀圖像處理時間約為14.46 ms，本文方法效率遠高于基于圖像塊匹配算法。

另外，對于階躍信號，在微動平臺t=1 s處突然運動，微動平臺動的瞬間速度較大，CCD相機采集的圖像較為模糊，因而對圖像二值化過程造成較大影響，圖6(a)記錄了不同時刻連通域3的面積變化，其中，直線是面積平均值，曲線是各時刻連通域3面積大小，從圖中可看出，在時刻t=1 s處，連通域3的面積發生劇烈變化，所對應的瞬間測量誤差較大，圖像較為模糊；而對于正弦信號，由于微動平臺運動相對平緩，因而連通域3面積變化不大，各個時刻測量誤差相對穩定。

圖6 連通域3在各不同采樣時刻面積變化

3.2 成像模型驗證

由于微動平臺是單自由度系統，根據上文所述針孔成像模型，根據式(2)，微動平臺在圖像空間的運動軌跡應該為一條直線。為驗證成像模型，圖7記錄了微動平臺沿1/4個周期的正弦信號運動時連通域3的重心坐標，其中,三角是不同時刻采樣點連通域3的坐標，直線為采用最小二乘法擬合的直線。可以看出：連通域3重心坐標基本符合直線分布，證明成像模型有效。

圖7 連通域3重心軌跡

4 結 論

通過建立成像模型，推導出圖像坐標系與世界坐標系之間的關系，然后將微視覺圖像二值化，形態學處理后提取連通域，通過追蹤連通域重心坐標計算微動平臺輸出位移。該方法具有高效率、高精度、簡單可靠等特點。實驗結果驗證了成像模型和位移測量算法的有效性，滿足了微動平臺輸出位移的測量要求。