鋼筋鋼纖維混凝土梁受壓區高度計算方法

曹國棟

(中鐵第一勘察設計院集團有限公司 陜西省鐵道及地下交通工程重點實驗室，陜西 西安 710043)

自19世紀20年代英國人Aspdin發明Portland水泥后，混凝土作為一種新型建筑材料在土木工程領域有著廣泛的應用。但混凝土也存在抗拉強度較低、易于開裂、性質較脆等缺點。鋼纖維混凝土是在普通混凝土中加入鋼纖維而組成的一種多相非均質復合材料[1]。與普通的鋼筋增強混凝土相比，它顯著地提高了混凝土原有的抗拉強度、抗彎強度、韌性及抗沖擊性,從而極大改變了混凝土的脆性[2]。

普通混凝土構件受壓區高度的研究在國內已有很多。鄭久建[3]基于單筋矩形截面鋼筋混凝土梁的受壓區高度計算公式進行了推廣,從而提出可以用于雙筋或T形截面鋼筋混凝土梁受壓區高度計算的統一公式。郭軍慶等[4]根據混凝土規范對鋼筋極限拉應變的限值和平截面的假定,推導出受彎構件極限狀態下截面受壓區最小高度。劉明亮[5]根據平截面假定和小偏心受壓構件的基本公式,提出了混凝土矩形截面小偏心受壓構件受壓區高度計算公式。姜雪晶[6]介紹了受彎構件正截面承載力計算的基本假定,并對相對界限受壓區高度的含義進行了探討。秦楠[7]分析了受壓區高度對受彎構件正截面的應力和相對余抗力的影響。郭恩等[8]詳細闡述了用一個公式求解矩形或T形截面受壓區高度的方法，并通過計算示例說明這種方法完全可行。王展生[9]將鋼筋混凝土T形梁受彎全過程分為4個階段(梁體開裂前階段、梁體開裂階段、壓區混凝土處于彈塑性階段和極限階段)，應用彈性理論對其受彎全過程進行分析，推導出各個階段的受壓區高度方程，通過求解得到受壓區高度的數值解，并推導出各個階段裂縫高度與受壓區高度關系式，結合受壓區高度的數值解，計算出裂縫高度值。王軍[10]以四周布筋混凝土墩柱構件為對象，從基本的力學概念出發，在彈性受力范圍內(即四周布筋混凝土橋墩在地震力作用下，鋼筋處于彈性狀態)分析了橋墩結構在受到地震作用時墩身開裂截面的受壓區高度。

雖然針對普通混凝土構件受壓區高度的研究很多，但針對鋼纖維混凝土梁構件受壓區高度的研究依然不足。另外，由于我國相關規范中混凝土受壓區高度的規定比較簡單，與實際情況不符。因此，需要對鋼纖維混凝土構件受壓區高度的計算方法進行研究，使其計算更準確。本文通過理論分析，得出鋼纖維混凝土構件受壓區高度計算公式，并通過試驗數據進行驗證，從而得出有益的結論。

1 受壓區高度規范取值及計算方法

1.1 受壓區高度規范取值

在GB 50010—2010《混凝土結構設計規范》[11](以下簡稱國標)中有效受拉區高度取hc,ef=h/2，h為梁高，受壓區形心距受拉區形心距離為0.87h0，h0為鋼筋形心到混凝土受壓區邊緣的距離,如圖1所示。

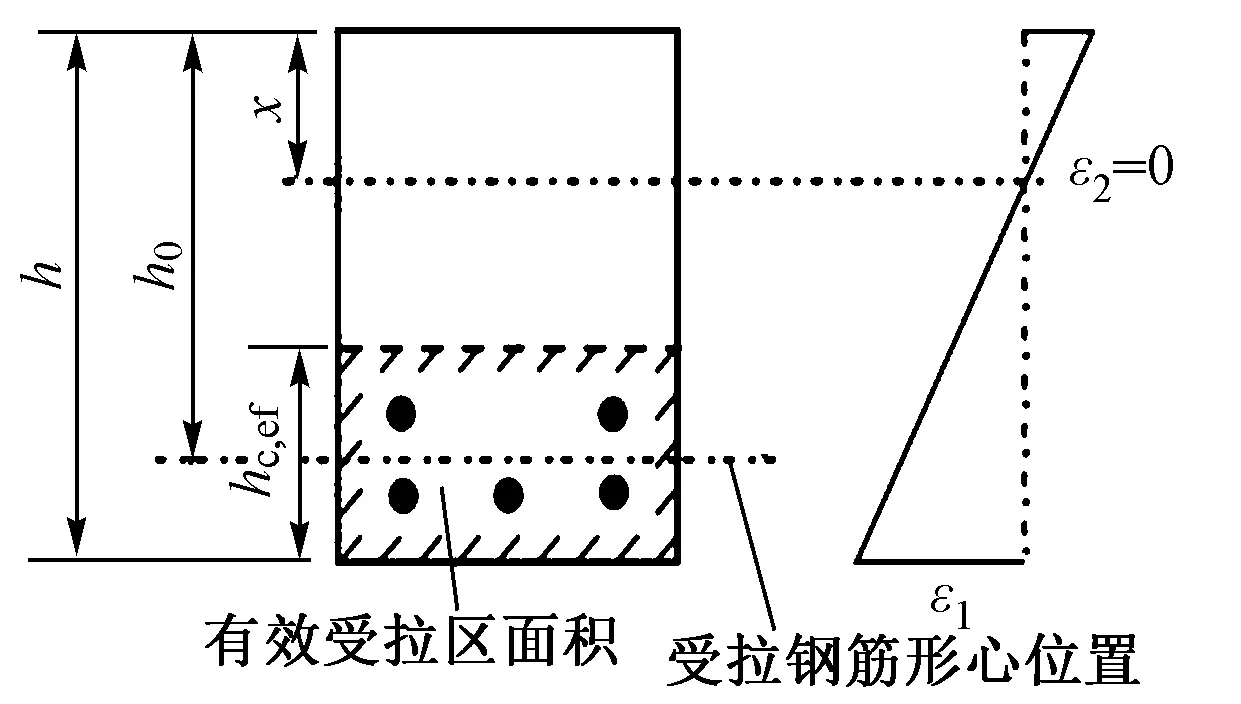
圖1 受拉區高度示意

在德國規范《DafStb Technical Rule on Steel Fiber Reinforced Concerte》[12](以下簡稱德標)中，有效受拉區高度取hc,ef= min[2.5(h-h0)，(h-x)/3，h/2]，即上述3者的最小值。

在國際規范《Fib Model Code for Concrete Structures 2010》[13](以下簡稱M-Code)中有效受拉區高度取hc,ef= min[2.5(h-h0)，(h-x)/3]，即上述二者的最小值。

對比國標、德標和M-Code 3部規范可以看出，國標的有效受拉區高度及受壓區高度均不隨外荷載變化而變化，與實際不符；而德標和M-Code的受壓區高度與受拉區高度均與外荷載有密切聯系，更合理。

1.2 受壓區高度計算方法

為準確計算鋼筋鋼纖維混凝土梁構件受壓區高度，依據平截面假定，從彈性力學角度對鋼纖維混凝土構件在開裂階段應力應變關系及軸力彎矩平衡方程進行分析。圖2為鋼纖維混凝土構件在混凝土開裂階段的應力應變分布狀態。

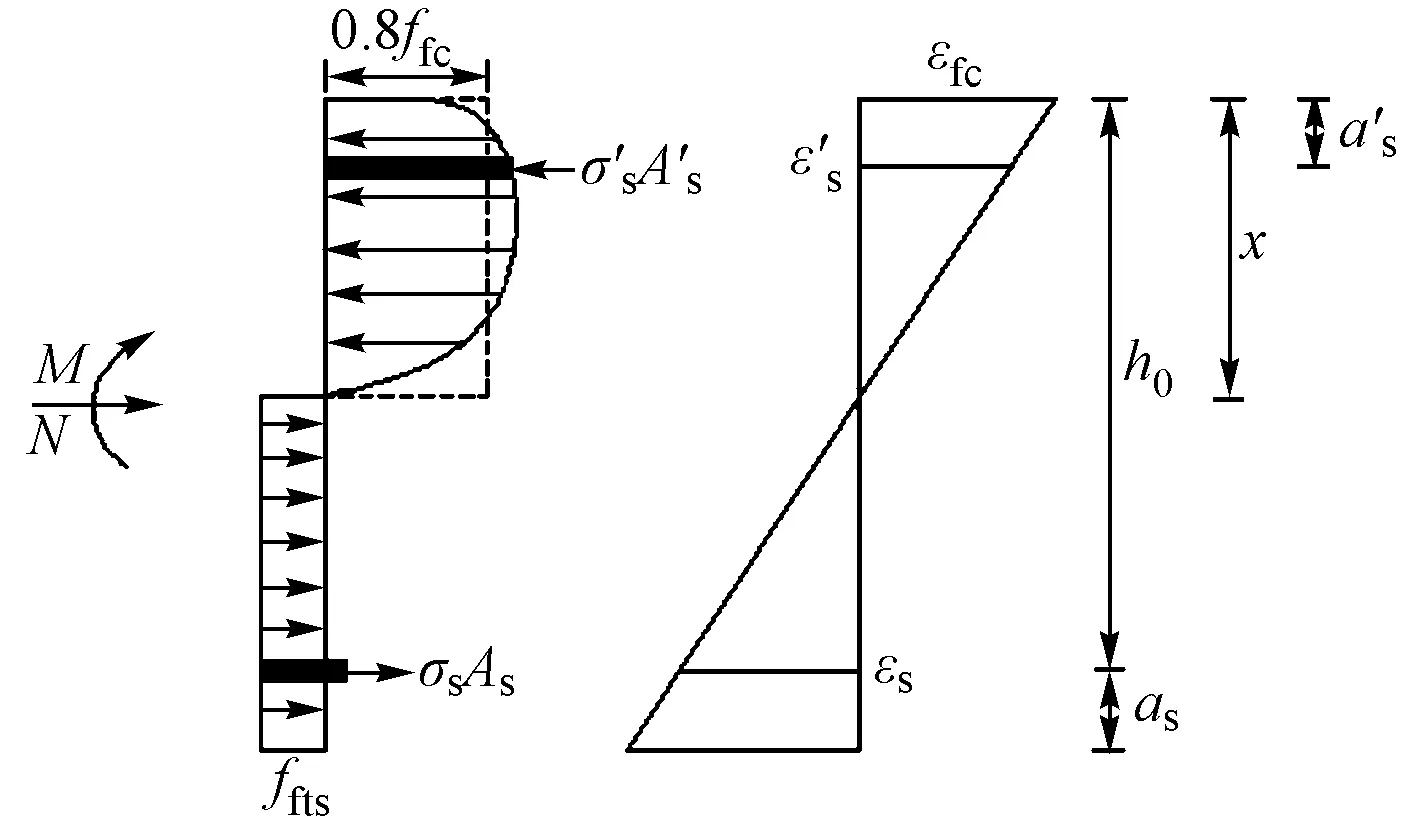
圖2 混凝土開裂階段應力應變分布

本構方程

ffc=Ecεfc

(1)

σs=Esεs

(2)

幾何方程(符合平截面假定)

(3)

(4)

軸力平衡方程

(5)

彎矩平衡方程(對受壓筋取矩)

(6)

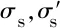
聯立式(1)—式(6)可得關于受壓區高度x的一元五次方程,設系數為A,B,C,D,E,F,則方程為

Ax5+Bx4+Cx3+Dx2+Ex+F=0

(7)

一元五次方程的解法有很多種，有迭代法、解析法等。使用EXCEL單變量求解迭代可求得受壓區高度值。

對于上式,當N=0時即為鋼纖維混凝土純彎構件受壓區高度計算公式；當ffts=0時即為普通混凝土壓彎構件計算公式。

2 M-Code裂縫寬度計算方法

由于受壓區高度在試驗過程中不易測量，而在計算混凝土裂縫寬度時受壓區高度的值直接決定了受拉鋼筋應力的取值，對結果影響很大，因此選取試驗的裂縫寬度值對受壓區高度計算公式進行評價。由文獻[14]可知，國標、德標和M-Code 3部規范均使用裂縫間距乘以鋼筋與混凝土的應變差來計算裂縫寬度。不同之處在于，國標與德標計算方法均在普通混凝土裂縫寬度基礎上考慮鋼纖維影響系數，而M-Code則進行直接的計算，即所有參數均為鋼纖維混凝土的相關力學參數。因此，針對鋼纖維混凝土構件受壓區高度的計算采用M-Code規范計算方法比較合適。

最大裂縫寬度ωf,max可由以下公式計算

ωf,max=2ls,max(εsm-εcm-εcs)

(8)

(9)

(10)

式中:ls,max為平均裂縫間距；εsm為裂縫間距內鋼筋的平均應變；εcm為裂縫間距內混凝土的平均應變；εcs為混凝土的收縮徐變；k為非均勻的自平衡應力影響系數;c為混凝土保護層厚度；fctm為鋼纖維混凝土平均抗拉強度；fFts為鋼纖維混凝土殘余抗拉強度；τm為平均黏結應力;deq為鋼筋有效直徑；ρte為構件有效配筋率；σsf為鋼纖維混凝土裂縫間鋼筋應力；σsr為鋼纖維混凝土開裂瞬間裂縫間鋼筋應力；β為相對滑移區域內的平均應變系數；ηr為混凝土收縮對應變的影響系數。

3 試驗分析

3.1 試驗概況

本次試驗總共有18根鋼纖維混凝土梁，其中12根為2組壓彎梁，配筋方案分別為4C12和3C12，其余6根為2組純彎梁，配筋方案分別為4C16和4C18；采用兩側對稱配筋。

梁試件加載布置如圖3所示，在試驗梁兩端用液壓千斤頂進行軸力加載，在梁中間2個三分點處同樣使用2個液壓千斤頂對梁試件進行豎向荷載的施加，水平與豎向的反力支撐由試驗臺架提供。

圖3 梁試件加載布置(單位：mm)

為保證試驗結果的準確性，采用豎向荷載與水平荷載成一定比例施加，最終達到試驗終止條件，即受拉鋼筋屈服或受壓混凝土破壞，停止試驗。試驗前通過理論計算分析確定純彎梁與壓彎梁的分級加載方案，實際分級加載時，在每一級加載停止后，通過系統控制保持荷載不變，等待試驗結果穩定后再讀取裂縫寬度。

為保證讀數準確性及裂縫寬度計算公式的適用范圍，選取試驗裂縫寬度0.2，0.3 mm的條件進行驗證。試驗梁相關參數見表1。

表1 試驗梁相關參數

3.2 試驗數據分析

依據上述理論分析及試驗數據，對受壓區高度進行分析，結果見表2。

表2 受壓區高度及裂縫寬度計算結果

為體現受壓區高度的變化狀態，將L1—L4中的8組數據分別對應編號為1～8，編號1～4為L1和L2組數據，編號5～8為L3和L4組數據。結合表2鋼纖維混凝土梁受壓區高度以及裂縫寬度的結果,得出國標和本文公式計算受壓區高度值與試驗組號的關系見圖4。國標與M-Code 2部規范計算裂縫寬度與試驗裂縫寬度為0.3 mm時的對比見圖5。

圖4 受壓高度與試驗組的變化關系

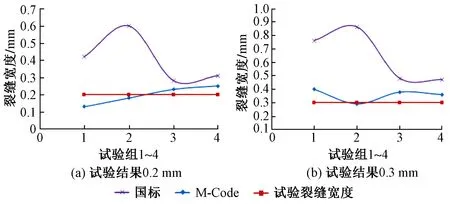
圖5 規范計算裂縫寬度與試驗結果對比

根據計算結果分析可知：

1)根據圖4中曲線的趨勢可以看出，壓彎梁部分國標與本文公式兩者相差甚遠，而純彎梁部分兩者更接近，這是由于壓彎梁受力模式因軸力的加入而更復雜，因此本文公式計算結果和國標計算結果相差更大。

2)根據圖5中規范裂縫寬度計算值與試驗結果的對比關系可以看出，裂縫寬度為0.2，0.3 mm 時，國標整體計算結果均明顯大于實際值，而使用本文公式的M-Code計算結果均與實際值比較吻合。

為比較國標與M-Code 2部規范裂縫計算的精確度，定義裂縫計算誤差率，計算公式如下式。

ζc=ωt-ωp/ωp

(11)

式中:ζc為裂縫計算誤差率;ωt為理論計算裂縫寬度;ωp為實際裂縫寬度。

計算結果與實際裂縫寬度誤差見表3。可知，國標計算結果誤差均比較大。

表3 計算誤差率統計 %

4 結論

本研究主要分析了鋼纖維混凝土受壓區高度的計算公式，并對比國標與M-Code 2部規范計算裂縫寬度的結果，得到以下幾點結論:

1)通過分析規范中受壓區高度計算方法，可知國標的計算方法有明顯缺陷，因此本文依據平截面假定，分析鋼纖維混凝土構件在開裂階段的應力應變關系，得出關于計算受壓區高度的一元五次方程公式。

2)選取國標與M-Code 2部規范計算的裂縫寬度值對受壓區高度計算公式進行評價，并對M-Code計算裂縫寬度的原理進行闡述。

3)對比受壓區高度值可以看出，國標規定的受壓區高度隨外部條件的變化基本不變，而本文提出公式計算的受壓區高度值隨外荷載等條件的變化而變化。

4)對比規范裂縫寬度計算值與試驗結果，國標整體計算結果均明顯大于實際值，而使用本文公式的M-Code 計算結果均與實際值比較吻合。

5)對于純彎與壓彎梁，國標的計算結果誤差均比較大,而本文計算受壓區高度的公式對于多種受力狀態均適用。