串并混聯(lián)四足仿生機器人動力學(xué)建模與分析

王曉磊 金振林 李曉丹 劉 祥

(1.燕山大學(xué)機械工程學(xué)院， 秦皇島 066004； 2.遼寧工業(yè)大學(xué)機械工程與自動化學(xué)院， 錦州 121001)

0 引言

由于仿生足式機器人通過對爬行動物運動機理分析進行結(jié)構(gòu)模仿設(shè)計[1]，因此，仿生足式機器人在復(fù)雜環(huán)境下行走具有良好的地形適應(yīng)能力，受到世界各研究機構(gòu)的廣泛關(guān)注。美國波士頓動力學(xué)公司設(shè)計了多種液壓驅(qū)動串聯(lián)腿部機構(gòu)的四足仿生機器人[2-4]，燕山大學(xué)設(shè)計、開發(fā)多款并聯(lián)、串并混聯(lián)腿部結(jié)構(gòu)的多足仿生機器人[5-8]，山東大學(xué)[9-10]、國防科學(xué)技術(shù)大學(xué)[11]、北京理工大學(xué)[12]、哈爾濱工業(yè)大學(xué)[13]等高校團隊對串聯(lián)腿部機構(gòu)的四足仿生機器人進行深入研究，上海交通大學(xué)高峰團隊采用并聯(lián)結(jié)構(gòu)機械腿研制了多足仿生機器人[14-15]。上述仿生機器人的腿部機構(gòu)大多是由純并聯(lián)機構(gòu)或由簡單的桿件串聯(lián)機構(gòu)組成。純并聯(lián)結(jié)構(gòu)承載能力大，但不適于快速行走；串聯(lián)結(jié)構(gòu)行走速度快，承載能力沒并聯(lián)機構(gòu)好。

對于仿生機器人來說，動力學(xué)分析可為系統(tǒng)動力參數(shù)選取提供依據(jù)，同時還可為機器人承載時軌跡規(guī)劃奠定基礎(chǔ)，因此對仿生機器人的動力學(xué)研究非常重要[16]。目前，對仿生機器人腿部機構(gòu)的動力學(xué)分析較少，文獻[17-20]均對腿部機構(gòu)的動力學(xué)進行了研究，但都只是對仿生機器人腿部機構(gòu)的伺服參數(shù)進行預(yù)估，而沒有對整個機器人在行走過程的動力學(xué)及移動能耗進行分析。本文研究一種串并混聯(lián)仿生機械腿，針對該四足機器人的腿部機構(gòu)進行動力學(xué)建模，并進行驗證、動力學(xué)分析及移動能耗分析，為動力參數(shù)與緩沖結(jié)構(gòu)設(shè)計及軌跡規(guī)劃奠定基礎(chǔ)。

1 運動學(xué)分析

運動學(xué)分析是研究動力學(xué)的基礎(chǔ)，包括位置分析、速度分析及加速度分析。本文主要對腿部結(jié)構(gòu)的位置和速度進行分析。

1.1 腿部模型

與上海交通大學(xué)聯(lián)合開發(fā)的四足機器人整體樣機及腿部機構(gòu)簡圖如圖1所示。該四足機器人由4條相同的腿部機構(gòu)組成，每條腿部機構(gòu)均具有3個自由度。該腿部機構(gòu)由平面并聯(lián)五桿機構(gòu)OABCD驅(qū)動雙菱形行程放大機構(gòu)實現(xiàn)并聯(lián)驅(qū)動，兩個直線驅(qū)動副的伸縮實現(xiàn)足端抬起和前后擺動。同時串聯(lián)部分有直線副驅(qū)動的四桿機構(gòu)MKNQ，實現(xiàn)五桿機構(gòu)及雙菱形機構(gòu)沿MP軸的側(cè)擺運動，實現(xiàn)側(cè)向解耦。通過這兩種機構(gòu)的組合實現(xiàn)了腿部機構(gòu)的前后邁步和側(cè)向邁步。由于本文研究的機器人屬于高性能四足仿生機器人，要求具有快速移動、承受高負(fù)載性能。因此，系統(tǒng)中直線驅(qū)動均采用伺服液壓缸驅(qū)動，使系統(tǒng)具有高動態(tài)性、大負(fù)載能力[21]。由于腿部機構(gòu)由并聯(lián)五桿機構(gòu)與雙菱形行程放大機構(gòu)組成，因此，直線驅(qū)動器只需移動很小的距離，就能獲得很大的工作空間，可實現(xiàn)快速行走；由于該腿部結(jié)構(gòu)采用了串并混聯(lián)機構(gòu)，較傳統(tǒng)的串聯(lián)機械腿相比，具有更大的承載能力，且轉(zhuǎn)向靈活。

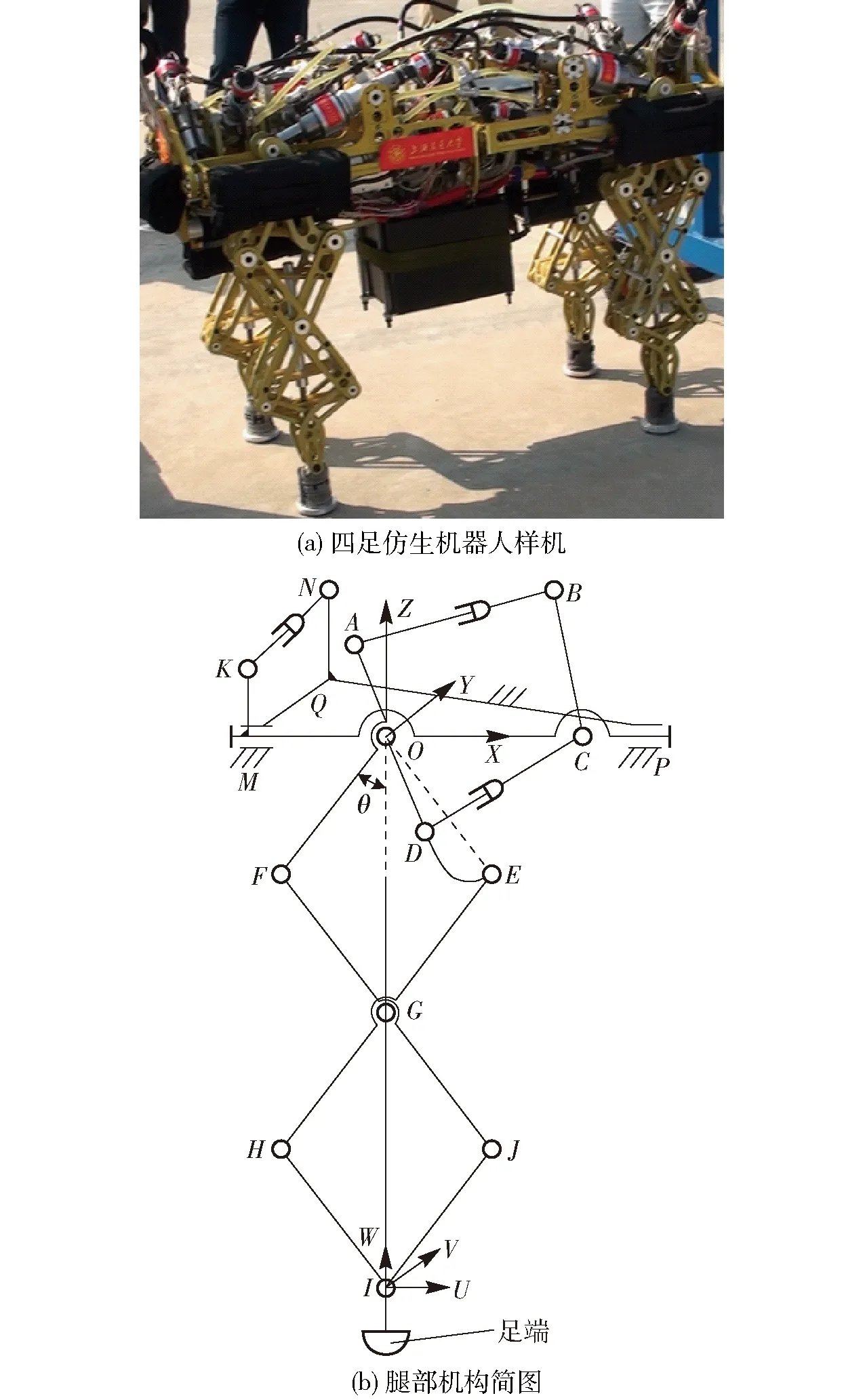
圖1 四足機器人整體樣機及腿部機構(gòu)簡圖Fig.1 Whole prototype and leg mechanism schematics of quadruped robot

1.2 位置分析

為了便于分析，建立圖1b所示的固定坐標(biāo)系OXYZ和動坐標(biāo)系IUVW。O為固定坐標(biāo)系原點，X軸沿OC方向，且在OMP平面內(nèi)，Z軸垂直于OMP平面向上，Y軸由右手螺旋法則確定。平面四桿機構(gòu)MKNQ平行于YOZ平面。設(shè)I為動坐系原點，W軸沿IO方向，U軸垂直W軸，向右，V軸由右手螺旋法則確定。設(shè)結(jié)構(gòu)參數(shù)‖OA‖=l1，‖AB‖=l2，‖BC‖=l3，‖CD‖=l4，‖OD‖=l5，‖OC‖=l6，‖MK‖=l7，‖KN‖=l8，‖NQ‖=l9，‖QM‖=l10，雙菱形OFGE和GHIJ邊長均為l，OF與OG夾角為θ。由圖1b可知，該腿部機構(gòu)具有沿X、Y軸轉(zhuǎn)動和沿Z向移動的自由度，所以在位置分析時，可先分析平面機構(gòu)末端位置的變化，再沿X軸旋轉(zhuǎn)φ得到，同時設(shè)平面機構(gòu)末端繞Y軸旋轉(zhuǎn)為φ。

結(jié)合圖1b，參考點I的位置可以寫成

(1)

根據(jù)式(1)可得

(2)

為了便于分析，將總的腿部結(jié)構(gòu)簡圖分為2個平面圖，如圖2所示。圖2a為平面并聯(lián)機構(gòu)簡圖，為未繞X軸旋轉(zhuǎn)時平面機構(gòu)的姿態(tài)，圖2b為四桿機構(gòu)MKNQ在YOZ面的投影圖。在圖2a中，AOF為一構(gòu)件，其中OF桿與X軸的夾角為β，OA與OF夾角為γ′。OE與X軸夾角為α，為了避免干涉，OE桿件不是直線，而是使OD與OE線有一夾角為γ。圖2b中，MK與Y軸夾角為θ6，KN與Y軸夾角為θ7。

圖2中的Ci為各液壓缸缸體、活塞桿、桿件及支架的質(zhì)心，其中C1、C3、C13為活塞桿質(zhì)心，C2、C4、C12為液壓缸缸體質(zhì)心，C9為桿件AOF的質(zhì)心，C10為桿件ODE的質(zhì)心，C7、C8為HI和JI質(zhì)心，并在桿件的中心點，C5、C6為桿件FJ和EH質(zhì)心,與G點重合，C11為腿部支架質(zhì)心，C14為足端及導(dǎo)向桿組件的質(zhì)心，各質(zhì)心點處的桿件空間角速度為ωi,速度為vCi。

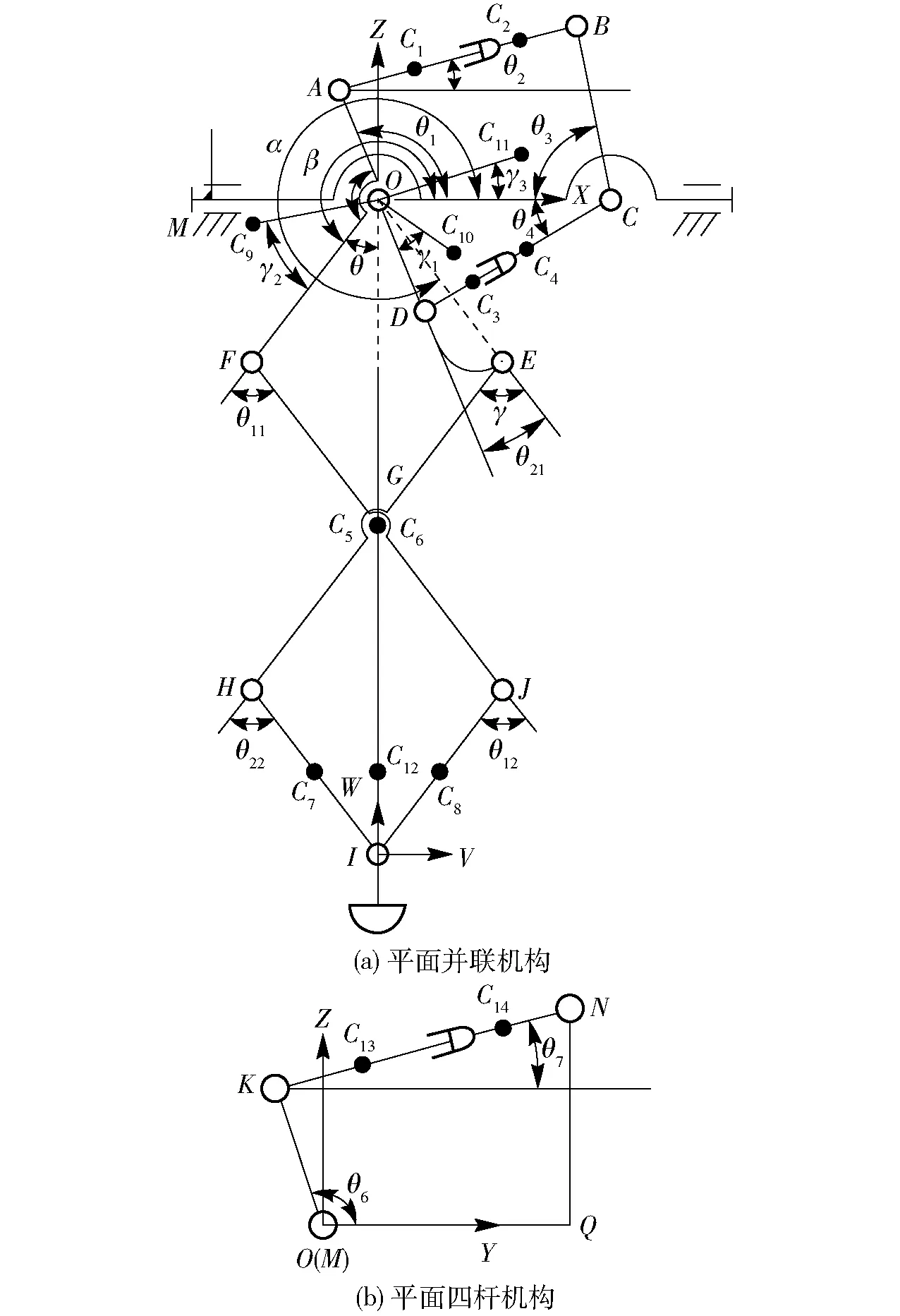
圖2 整體腿部結(jié)構(gòu)拆分圖Fig.2 Breakdown diagrams of overall leg structure

結(jié)合圖2a，根據(jù)結(jié)構(gòu)約束條件可得到

(3)

(4)

根據(jù)式(4)得

(5)

將式(3)代入式(5)得

(6)

同理根據(jù)結(jié)構(gòu)約束條件可知，OABC、ODC均為一個矢量環(huán)，可寫成

(7)

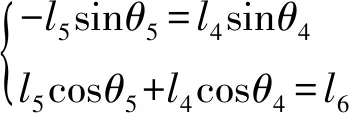
(8)

結(jié)合圖2b，同理由結(jié)構(gòu)約束條件得到

(9)

(10)

若已知該腿部機構(gòu)末端I的位置，根據(jù)式(1)、(2)即可求出φ、θ、φ，再根據(jù)式(5)求出θ5、θ1，根據(jù)式(7)、(8)在平面機構(gòu)中即可求出l2、l4；根據(jù)式(9)求得θ6，根據(jù)式(10)求得l8，即為腿部機構(gòu)的位置反解。

1.3 運動工作空間

給定結(jié)構(gòu)參數(shù)l=260 mm，l1=l5=50 mm，γ=15°，γ′=135°，l3=155 mm，l6=305 mm，θ3=75°。設(shè)約束條件為15°≤θ≤75°，-15°≤φ≤15°，255 mm≤(l2、l4、l8)≤340 mm。根據(jù)位置方程與約束條件，通過Matlab繪制腿部機構(gòu)的工作空間，如圖3所示。

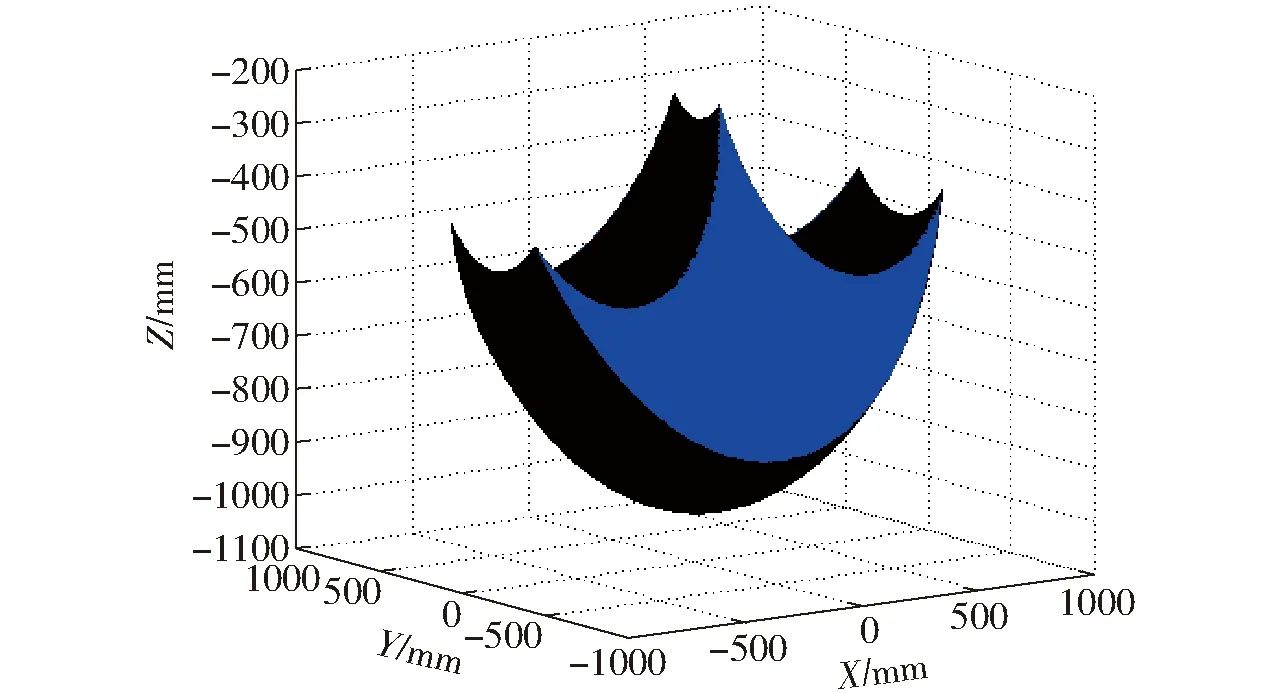
圖3 腿部機構(gòu)工作空間Fig.3 Workspace of leg mechanism

從圖3可以看出，桿長變化量在0～85 mm內(nèi)，沿X軸的長度可達1 000 mm，沿Z軸的工作空間高度最大可達450 mm。由此可知，該機構(gòu)驅(qū)動桿通過雙菱形機構(gòu)將末端行程放大，且隨位置的不同，放大倍數(shù)不同，越處于下部放大倍數(shù)越大。

1.4 線速度

為了進行腿部結(jié)構(gòu)的動力學(xué)分析，需要推導(dǎo)輸入與輸出的線速度映射關(guān)系。

分別對式(3)、(4)求導(dǎo)整理得

(11)

對式(7)進行求導(dǎo)得

(12)

(13)

對式(8)求導(dǎo)得

(14)

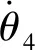
(15)

對式(9)、(10)求導(dǎo)得

(16)

(17)

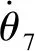
(18)

將式(13)、(15)分別代入式(11)可得

(19)

對式(1)求導(dǎo)得

(20)

(21)

(22)

將式(22)乘cosφ加上式(21)乘sinφ，整理得

(23)

將式(23)代入式(18)，可得

(24)

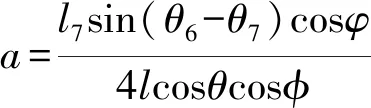
將式(20)乘cosφsinφ加上式(21)乘sinφ得

(25)

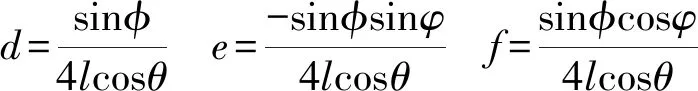
由式(20)得

(26)

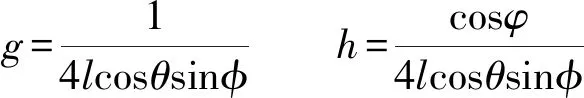
由式(11)、(25)、(26)得

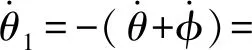
(27)

(28)

將式(27)、(28)分別代入式(13)、(15)得

(29)

(30)

將式(29)、(30)、(24)寫成矩陣形式

(31)

其中

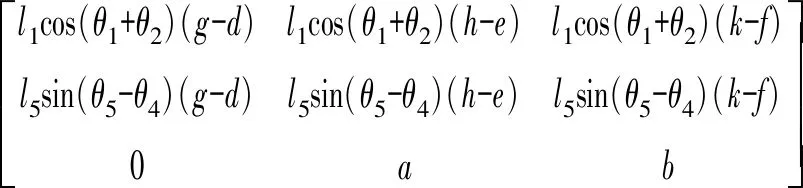
同時可得

(32)

(33)

(34)

1.5 桿件角速度

根據(jù)式(18)、(34)、(31)得圖2a平面機構(gòu)的下液壓缸角速度為

(35)

其中

式中GV2：——GV中第2行元素

根據(jù)式(12)、(27)、(31)可得在圖2a平面機構(gòu)的上液壓缸角速度為

(36)

其中

式中GV1：——GV中第1行元素

同理，平面機構(gòu)中下液壓缸在空間的角速度可通過角速度疊加原理及式(35)得到

ωi=Giv(i=3,4)

(37)

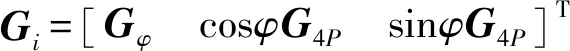
平面機構(gòu)中上液壓缸在空間的角速度可通過角速度疊加原理及式(36)得到

ωi=Giv(i=1,2)

(38)

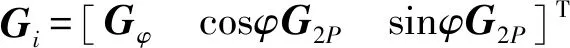
根據(jù)圖2a平面機構(gòu)圖的幾何約束可知

θ11=-θ12=2θ

(39)

-θ21=θ12=2θ

(40)

對式(39)、(40)求導(dǎo)可得

(41)

(42)

FGJ桿、EGH桿在空間的角速度可通過角速度疊加原理及式(31)、(33)、(13)、(15)、(41)、(42)、(30)得

ω5=G5v

(43)

ω6=G6v

(44)

其中

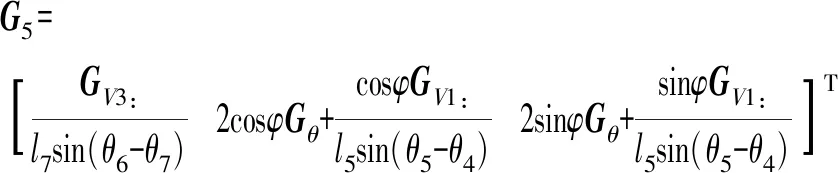
式中GV3：——GV中第3行元素

對于JI桿、EI桿空間角速度通過角速度疊加原理及式(31)、(33)、(13)、(15)、(30)、(43)、(44)得

ω8=G8v

(45)

ω7=G7v

(46)

其中

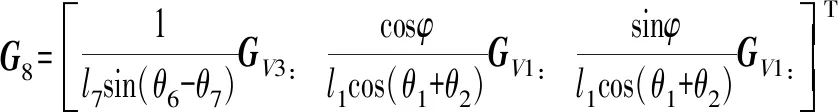
對于只存在轉(zhuǎn)動AOF桿在空間的角速度通過角速度疊加原理與式(13)、(31)得

ω9=G9v

(47)

其中

對于ODE桿空間角速度通過角速度疊加原理及式(15)、(30)得

ω10=G10v

(48)

其中

支架角速度即為繞X軸的角速度，即

(49)

其中

足端的角速度通過角速度疊加原理得

(50)

將式(34)代入式(50)得

ω12=G12v

(51)

其中

根據(jù)式(16)、(17)、(31)可得擺動液壓缸角速度

(52)

其中

側(cè)擺液壓缸在空間的角速度為

(53)

其中

即得到了機構(gòu)中所有桿件的角速度。

1.6 桿件質(zhì)心的位置及速度

上液壓缸活塞桿及缸體質(zhì)心在空間矢量可分別表示為

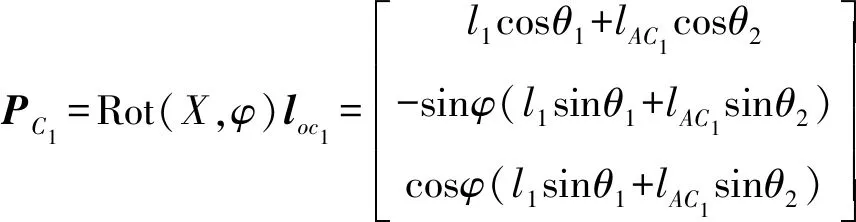
(54)

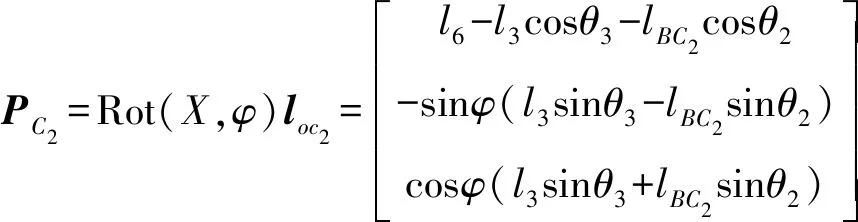
(55)

式中l(wèi)oc1、loc2——平面機構(gòu)中的矢量

同時對式(54)、(55)求導(dǎo)得

(56)

(57)

其中

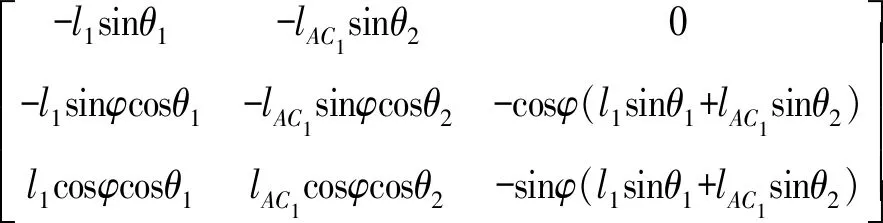
將式(12)、(13)、(30)、(33)代入式(56)、(57)得

vC1=GC1v

(58)

vC2=GC2v

(59)

其中

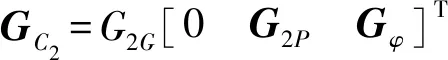
同理，下液壓缸活塞桿及缸體的質(zhì)心矢量可表示為

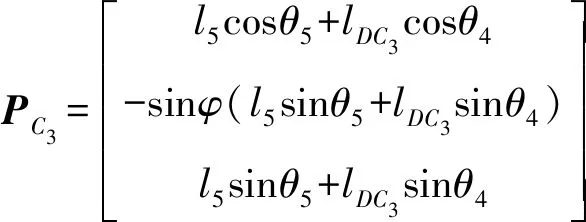
(60)

(61)

對式(60)、(61)求導(dǎo)得

(62)

(63)

其中

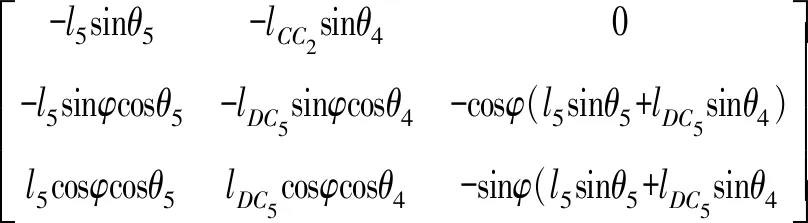
將式(14)、(15)、(30)、(33)代入式(62)、(63)得

vC3=GC3v

(64)

vC4=GC4v

(65)

其中

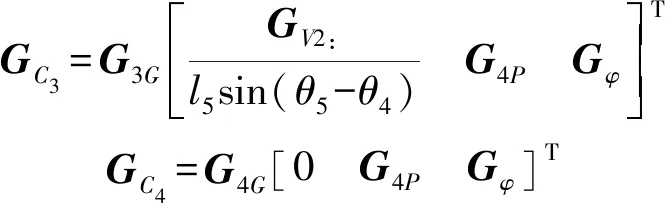
桿EGH與桿FGH均是對稱結(jié)構(gòu)，設(shè)其質(zhì)心均在G點，線速度為末端速度的一半，即

vC5=vC6=GC5v=GC6v=0.5v

(66)

由于桿EGH與桿FGH在機構(gòu)中間部位，其質(zhì)心位置在G點，則位置矢量為

PC5=PC6=0.5p

(67)

在空間中桿HI、JI質(zhì)心的位置可分別通過矢量疊加得

(68)

(69)

對式(68)、(69)求導(dǎo)可得

(70)

(71)

其中

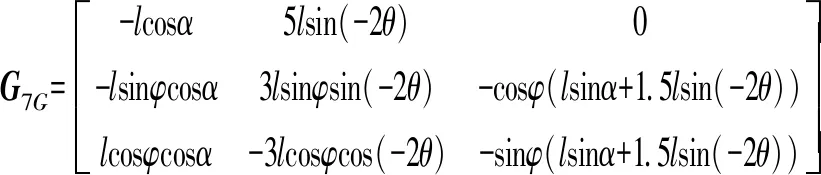
將式(13)、(15)、(30)～(32)代入式(70)、(71)得

vC7=GC7v

(72)

vC8=GC8v

(73)

其中

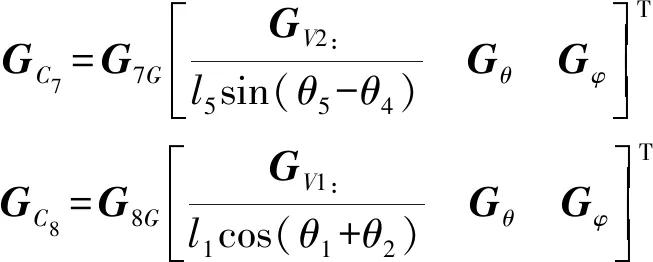
桿AOF及桿ODE重心的位置矢量可表示為

(74)

(75)

對式(74)、(75)求導(dǎo)得

(76)

(77)

其中

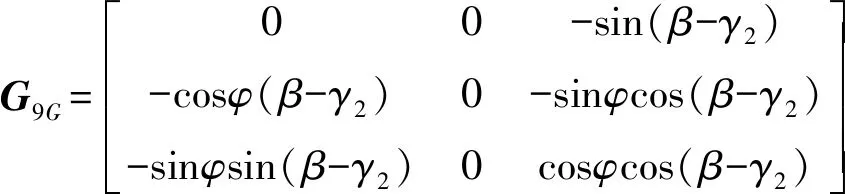
將式(33)、 (13)、 (15)、(30)代入式(76)、(77)得

vC9=GC9v

(78)

vC10=GC10v

(79)

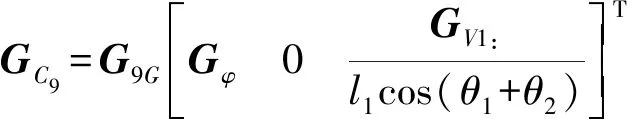
架體為對稱結(jié)構(gòu)，中心的位置矢量為

(80)

由于此件只做純轉(zhuǎn)動，在計算動能時已計算轉(zhuǎn)動動能，故可認(rèn)為vC11=0。

足端位置矢量為

(81)

vC12=GC12v

(82)

式中GC12——單位矩陣

擺動缸活塞桿質(zhì)心位置及缸筒質(zhì)心空間位置矢量為

PC13=[0lKC13cosθ7+lMKcosθ6lKC13sinθ7+lMKsinθ6]T

(83)

PC14=[0lOQ-lNC14cosθ7lQN-lNC14sinθ6]T

(84)

對式(83)求導(dǎo)得

(85)

將式(30)代入式(85)得

vC13=GC13v

(86)

其中

GC13=

由于此件只作純轉(zhuǎn)動，在計算動能時已計算轉(zhuǎn)動動能，故可認(rèn)為vC14=0。

2 動力學(xué)建模

為了簡化腿部機構(gòu)動力學(xué)建模，需要假設(shè)整個機器人都是由金屬材料構(gòu)成，各構(gòu)件認(rèn)為是剛體，彈性變形忽略不計；各轉(zhuǎn)軸質(zhì)量較小、且轉(zhuǎn)動慣量較小，認(rèn)為是構(gòu)件一部分，且沒有繞軸線的自轉(zhuǎn)；活塞及活塞桿認(rèn)為是一個整體，也無繞活塞桿軸線的自轉(zhuǎn)，足端導(dǎo)向套、足端和彈簧視為一個整體。

2.1 廣義力與驅(qū)動力的映射

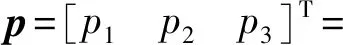
(87)

將式(30)代入式(87)得

(88)

2.2 各構(gòu)件能量

腿部機構(gòu)能量主要由各構(gòu)件的動能和勢能組成。對于單個腿部機構(gòu)的構(gòu)件主要有3個液壓缸缸體、3個液壓缸缸體活塞桿、腿部支架、桿EGH、桿FGH、桿AOE、桿ODF、桿EJ與桿FH及足端。

對于組成機械腿機構(gòu)的所有構(gòu)件相對于固定坐標(biāo)系的動能為

(89)

式中In——腿部機構(gòu)各構(gòu)件繞其質(zhì)心的慣量矩陣

mn——腿部機構(gòu)各構(gòu)件的質(zhì)量矩陣

vCn——腿部機構(gòu)各構(gòu)件質(zhì)心處的速度矢量

ωn——腿部機構(gòu)各構(gòu)件質(zhì)心處角速度矢量

依據(jù)運動學(xué)分析，將ωn、vCn對應(yīng)于廣義速度v的表達式代入式(89)整理得

(90)

其中

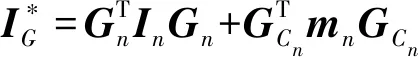
組成機械腿機構(gòu)的所有構(gòu)件相對于固定坐標(biāo)系的勢能為

(91)

2.3 腿部機構(gòu)動力學(xué)方程

建立動力學(xué)方程的方法有拉格朗日法[22]、虛功原理法[23]、凱恩法[24]等。由于拉格朗日方法從能量的角度出發(fā)，得到的動力學(xué)方程形式相對簡單[22]，所以采用拉格朗日法建立腿部機構(gòu)的動力學(xué)方程，其方程形式為

(92)

其中

L=T-U

式中L——拉格朗日函數(shù)

pi——腿部參考點I的廣義坐標(biāo)

fi——未考慮外部負(fù)載的足端力

將式(89)、(91)代入式(92)可得

(93)

由于勢能不是速度的函數(shù)[25]，所以整理式(93)得

(94)

(95)

其中

對式(95)時間求導(dǎo)

(96)

將式(90)對p1求導(dǎo)

(97)

將式(91)對p1求導(dǎo)可得

(98)

將式(95)～(97)代入式(94)整理得

(99)

其中

同理可求得

(100)

(101)

其中

整理式(99)～(101)寫成矩陣

(102)

其中

式中D——腿部機構(gòu)的廣義慣性矩陣

H——腿部機構(gòu)的離心力和哥氏力系數(shù)

Wg——腿部機構(gòu)的重力項

上述動力學(xué)方程建立的過程沒有考慮腿部機構(gòu)承受的外負(fù)載，設(shè)腿部機構(gòu)承受的外負(fù)載為Q。因此，當(dāng)考慮足端外負(fù)載時，動力學(xué)方程變?yōu)?/p>

F=f+Q

(103)

在仿生機器人行走過程中，腿部機構(gòu)需要具備擺動相和支撐相。擺動相是指在機器人行走過程中腿部機構(gòu)向前端或側(cè)面邁步，足端離開地面，不受外部的負(fù)載, 則Q為零。支撐相是指腿部足端著地，支撐軀體向前或側(cè)面行走，此時在足端承受外負(fù)載Q為足端與地面的接觸力。

通過式(88)可以得出腿部機構(gòu)的剛體逆動力學(xué)方程為

τ=JF

(104)

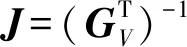
式中J——驅(qū)動力的雅可比矩陣

當(dāng)腿部結(jié)構(gòu)確定后，各桿件的質(zhì)量、轉(zhuǎn)動慣量均可由三維軟件得到；當(dāng)腿部機構(gòu)末端運動軌跡函數(shù)確定后，即可求出末端速度、加速度，根據(jù)式(104)即可得到對應(yīng)關(guān)節(jié)的驅(qū)動力。

3 動力學(xué)模型驗證與分析

3.1 動力學(xué)模型驗證

對于四足機器人的行走一般采用對角步態(tài)，對角兩條腿同時處于擺動相或者支撐相。由于拋物線適應(yīng)能力強，所以X向或Y向的運動軌跡可以寫成

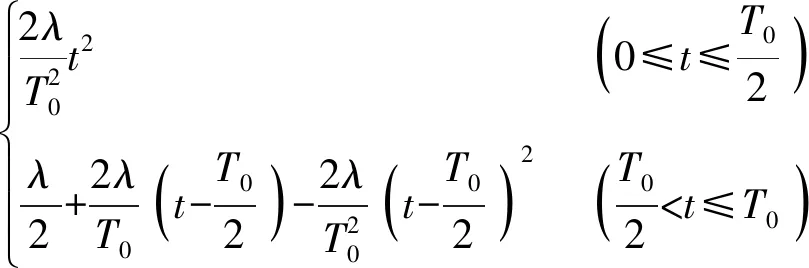
(105)

式中λ——步長，mm

T0——周期，s

對于Z向，為了減少沖擊與實現(xiàn)跨越障礙，采取正弦曲線，其軌跡為

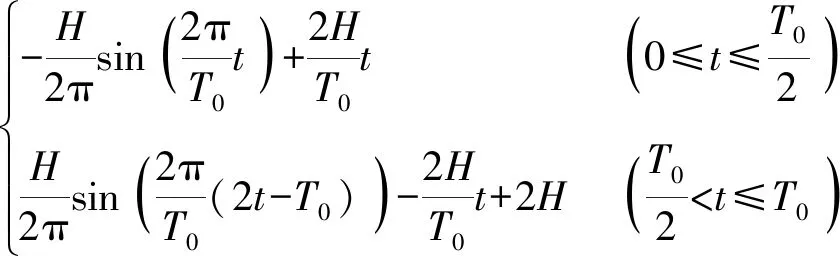
(106)

式中H——抬腿高度,mm

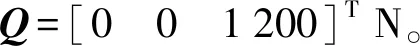
為了驗證模型的正確性，首先根據(jù)動力模型通過Matlab編程得到的3個液壓缸理論力的變化曲線。然后將所建立的樣機模型導(dǎo)入到ADAMS中，并將同樣的步態(tài)通過運動學(xué)反解推導(dǎo)出3個液壓缸的運動變化曲線，分別施加在相應(yīng)的液壓缸上，同時在末端在1～2 s間施加1 200 N的力，通過ADAMS軟件仿真得到3個液壓缸力的變化曲線。最后將兩條曲線擬合，如圖4a所示；并繪制出圖4b理論力與ADAMS仿真力在各時刻的誤差。從圖4可以看出，二者曲線變化基本一致，誤差在-1.731～1.774 N之間，驗證了理論推導(dǎo)模型的正確性。

圖4 驗證曲線Fig.4 Verified curves

由圖4可知，一條腿上3個液壓缸的最大輸出力均在腿部機構(gòu)著地瞬間產(chǎn)生，與抬腿高度無關(guān)；此時對地面沖擊力較大，所以在足端加了彈簧緩沖裝置，避免沖擊力過大，導(dǎo)致機構(gòu)損壞；3個液壓缸中最大輸出力為側(cè)擺液壓缸，因為此液壓缸與平面并聯(lián)機構(gòu)串聯(lián)，且為行程放大機構(gòu)，屬于費力杠桿。

3.2 步長對驅(qū)動缸最大輸出力的影響規(guī)律分析

通過以上分析可知，各驅(qū)動液壓缸的最大輸出力產(chǎn)生在腿部機構(gòu)著地的瞬間，所以各驅(qū)動缸在相同步態(tài)函數(shù)、相同周期下，只與步長有關(guān)。在機器人直線行走時，此時側(cè)擺缸輸出力為0。設(shè)此種步態(tài)下，機器人最大步長為900 mm、抬腿高度為150 mm時，不同步長的平面機構(gòu)液壓缸最大輸出力規(guī)律如圖5a所示。機器人側(cè)向移動時，側(cè)擺步長不能太大，過大會產(chǎn)生拌腿或側(cè)翻。此時設(shè)抬腿高度為200 mm時，步長最大值設(shè)為250 mm時，在不同步長時側(cè)擺缸最大輸出力規(guī)律如圖5b所示。

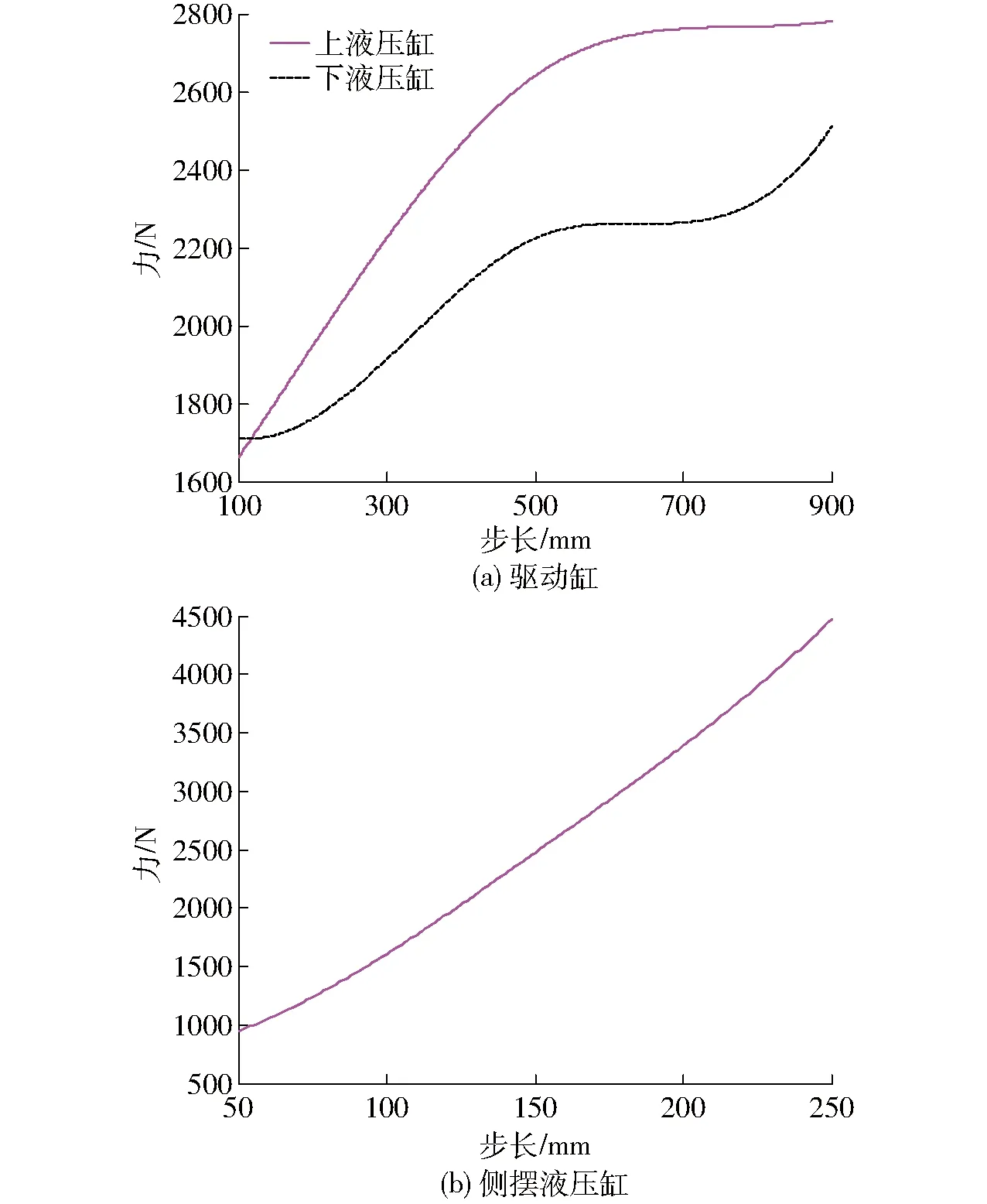
圖5 步長對驅(qū)動缸最大輸出力影響規(guī)律Fig.5 Effect of step length on maximum output force of drive cylinder

從圖5a可以看出，在直線行走時，并聯(lián)機構(gòu)的兩個液壓缸輸出最大力總體呈遞增趨勢，位于并聯(lián)機構(gòu)上方的液壓缸最大輸出力逐漸增大，達700～900 mm趨于平緩；位于下方的液壓缸相對上缸變化稍有平緩，但也在逐漸增大的。從圖5b可以看出，在側(cè)向行走時，側(cè)擺缸輸出最大力隨側(cè)擺步長的增加接近直線遞增，說明側(cè)擺對側(cè)擺液壓缸的最大輸出力影響較大。確定系統(tǒng)的最大壓力時，應(yīng)由側(cè)擺缸的最大輸出力決定，側(cè)擺缸最大輸出力的確定為系統(tǒng)的動力參數(shù)及腿部機構(gòu)緩沖結(jié)構(gòu)設(shè)計提供依據(jù)。

3.3 基于腿部動力學(xué)的能耗分析

3.3.1能耗指標(biāo)建立

多足步行機器人能耗的影響因素有很多，如機器人結(jié)構(gòu)參數(shù)、步態(tài)參數(shù)等。由于周期不同、步態(tài)參數(shù)不同、承載不同，機器人消耗的能量也不同。為了評價步行機器人在移動過程消耗能量，需要建立機器人能耗性能指標(biāo)。設(shè)定四足機器人的行走周期為1 s，設(shè)定機器人的能耗性能評價指標(biāo)為

(107)

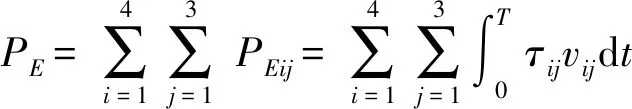
(108)

式中PE——一個周期內(nèi)機器人在移動過程中所有關(guān)節(jié)消耗的總能量

m——機器人自身質(zhì)量與外負(fù)載質(zhì)量之和

g——重力加速度

L1——1 s內(nèi)機器人移動的步長

PEij——第i條腿的第j個驅(qū)動缸輸出能量

τij——t時刻第i條腿第j個驅(qū)動缸輸出力

vij——t時刻第i條腿第j個驅(qū)動缸輸出速度

該性能指標(biāo)是移動單位步長、單位質(zhì)量機器人能耗的總和，且該值越小越好，代表能量利用率高。

3.3.2能耗指標(biāo)分析

由于機器人已經(jīng)完成設(shè)計，結(jié)構(gòu)參數(shù)不變，步態(tài)函數(shù)采用式(105)、(106)，也不變，故不考慮這兩種因素對能耗的影響，本文重點考慮步態(tài)參數(shù)對能耗的影響。由于前文已設(shè)定步態(tài)周期為1 s，所以只考慮步態(tài)參數(shù)的步長、抬腿高度對移動能耗指標(biāo)的影響。在行走過程中，主要分析包括直線行走和側(cè)向行走2種步態(tài)。

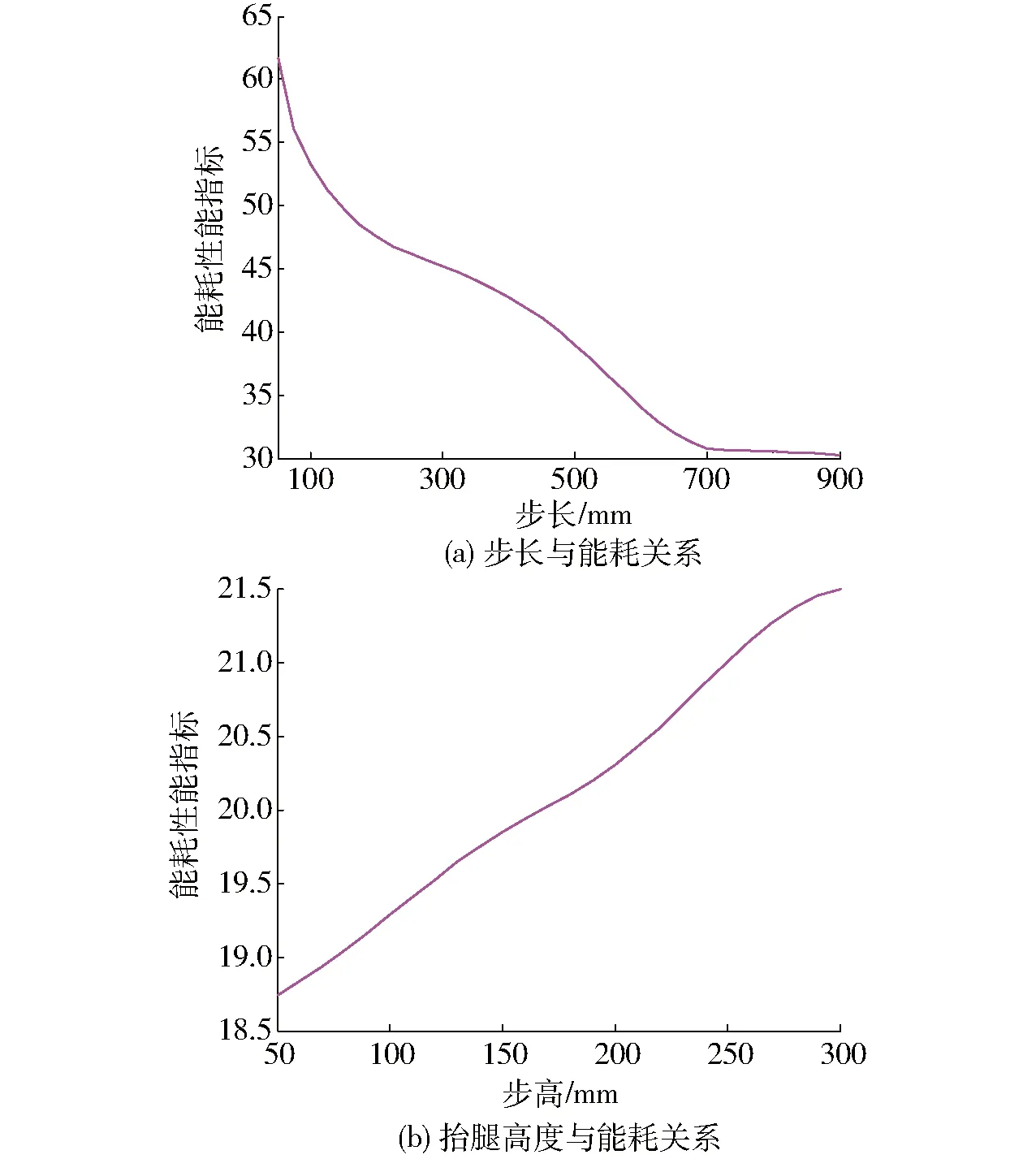
圖6 直行步態(tài)參數(shù)與能耗指標(biāo)關(guān)系Fig.6 Relationship between walking gait parameters and energy consumption indicators

(1)當(dāng)直線行走時，設(shè)定步高為100 mm，步長在100～900 mm之間變化，根據(jù)式(107)可計算出直線行走過程中不同步長的能耗性能指標(biāo)，并繪制出如圖6a所示的變化規(guī)律曲線。當(dāng)設(shè)定步長為600 mm，抬腿高度在50～300 mm之間，根據(jù)式(107)可計算出直線行走過程中不同抬腿高度的能耗性能指標(biāo)，并繪制出如圖6b所示的變化規(guī)律曲線。

從圖6a可看出，隨著步長的增加，能耗指標(biāo)單調(diào)遞減，到達700～900 mm后能耗指標(biāo)基本保持穩(wěn)定。表明隨著步長的增加，能量利用率越來越好。從圖6b可以看出，隨著抬腿高度的增加，能耗指標(biāo)呈單調(diào)遞增的趨勢，說明能量利用率越來越低。因此，在直線行走時，若要節(jié)約能源，應(yīng)該采取大步伐、小步高的軌跡規(guī)劃策略。在滿足要求條件下，步長在700～900 mm為好。

(2)當(dāng)機器人側(cè)向行走時，設(shè)定步高為50 mm,步長在50～250 mm變化，繪制的能耗性能指標(biāo)與步長的變化規(guī)律如圖7a所示。當(dāng)步長一定，步高在50～250 mm時，繪制的能耗性能指標(biāo)與抬腿高度的變化規(guī)律曲線如圖7b所示。從圖7a可以看出，機器人側(cè)向移動時，能耗指標(biāo)在步長50～100 mm之間隨著側(cè)向步長增加而減小，但超過100 mm時隨著步長增加而單調(diào)遞增，說明消耗的能量越大，在步長為100 mm能耗指標(biāo)最優(yōu)。從圖7b可以看出，隨著側(cè)向抬腿高度的增加，能耗指標(biāo)呈單調(diào)遞增的趨勢，說明能耗越來越大。因此，在機器人側(cè)向行走時，應(yīng)采取步長為100 mm左右、小步高的軌跡控制策略。

4 結(jié)論

(1)針對串并混聯(lián)四足仿生機器人腿部機構(gòu)進行了運動學(xué)分析，建立了各構(gòu)件速度與末端線速度的顯式表達式；通過各構(gòu)件的顯式表達式推導(dǎo)出正動力學(xué)方程，并建立了逆動力學(xué)方程。

(2)通過實例繪制了理論推導(dǎo)曲線和ADAMS虛擬樣機仿真曲線，驗證了理論推導(dǎo)的正確性。仿真結(jié)果表明，驅(qū)動缸在腿部足端接觸地的瞬間產(chǎn)生最大輸出力；分析得到了不同步長情況下，各驅(qū)動液壓缸最大輸出力的變化規(guī)律；在有側(cè)向移動的步態(tài)中，3個驅(qū)動缸中的側(cè)擺缸輸出力最大。

(3)建立了仿生機器人的能耗性能指標(biāo)，分析了不同步態(tài)參數(shù)對能耗性能指標(biāo)的影響規(guī)律，得到了減少能耗的方法。

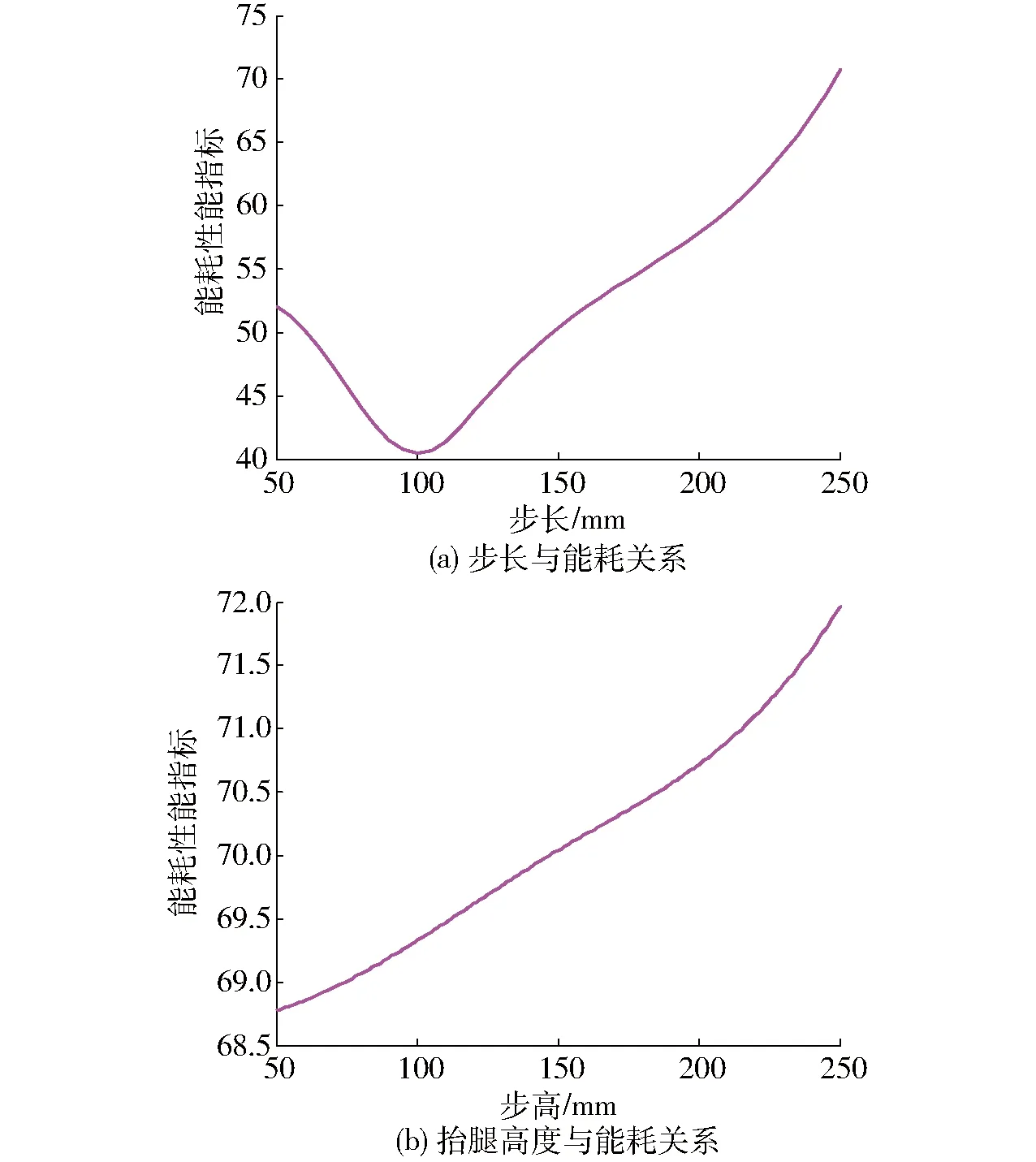
圖7 側(cè)向行走步態(tài)參數(shù)與能耗關(guān)系Fig.7 Relationship between lateral walking gait parameters and energy consumption