6-UPS并聯機器人快速正向運動學研究

劉艷梨 吳洪濤 李 耀 王若冰 徐媛媛 陳 柏

(1.南京航空航天大學機電學院， 南京 210016； 2.江蘇安全技術職業學院機械工程系， 徐州 221011；3.南通理工學院機械工程學院， 南通 226002)

0 引言

現有的求解6-UPS并聯機器人正向運動學方法[1]可概括為多項式、添加傳感器、數值迭代3類方法，這些方法不具備實時反饋的能力。多項式方法可以通過采用對偶四元數方法[2]、特殊的幾何性質[3]、Gr?bner基算法[4-5]、區間分析[6]和代數消元[7-8]等方法求解非線性方程組，化簡得到一元40、20、17、14次的代數方程，最終得到所有可能解，包括無理復根和增根的所有解，運動學正解多解對應多種裝配模式，且計算時間長，給實時反饋控制帶來困難。文獻[9]采用方位特征集方法得到了全解析算法，解決了多解容易產生增根、出現失根問題。傳感器方法通過添加4個[10]、3個[11]、2個[12]甚至1個傳感器[13-14]來輔助計算正向運動學，能夠得到較好結果，但是，添加傳感器不但增加了硬件成本，還引入傳感器測量誤差等問題。文獻[13]采用傳感器方法得到唯一位姿，但是推導過程繁瑣，計算時間較長。數值迭代方法關鍵是選取一個合適的初始值，如果初值選取得當，使用牛頓-拉夫森迭代方法可以得到唯一解[15-18]，否則會影響系統的魯棒性，同時無法得到所有的裝配模式。文獻[19]采用四元數得到了正向運動學的快速數值解，消除了姿態矩陣的數學奇異性，是一個較好的數值方法。文獻[20]研究了冗余驅動的數值解，消除了算法中位置和姿態的數學奇異性。文獻[21]采用齊次坐標變換求解反向運動學。文獻[22]采用由點和方位矢量形成的自然坐標法來描述多體系統的位置，而沒有使用角度坐標。文獻[23]利用鏈路的自然坐標來描述相鄰鏈路的相對運動，這些自然坐標僅描述機構與所選擇的相對系統之間的關系，而不管機構的運動學結構。文獻[24]通過選擇合適的點和方位矢量形成的自然坐標描述多體系統，建立了一個合適的模型。文獻[25]提出了用自然坐標表示的致動器的驅動力公式。采用自然坐標方法描述系統運動學，可有利于建立二次或線性的運動學方程組，能避免三角函數等超越函數計算。

本文將并聯機器人運動參數選為若干點的坐標，選擇平面平臺型6-UPS并聯機器人動平臺平面中2個動坐標軸端點和坐標軸原點為代表點，將并聯機器人運動學表示為3個代表點坐標的函數形式，建立9個一次和二次多項式方程，進行消元處理，得到6個二次多項式方程，在此基礎上，改進牛頓-拉夫森迭代算法，最終求解得到唯一一組位置和姿態參數。

1 6-UPS并聯機器人運動學基礎

1.1 結構

6-UPS并聯機器人及其坐標系如圖1所示。該機構包括動、靜上下2個平臺和6條結構一致支腿組成，各個支腿和動平臺之間通過球鉸S連接，和靜平臺之間通過虎克鉸U連接，支腿上有移動副P，通過對P施加驅動，來保證整個平臺的期望運動。該機構屬于平面平臺型，即動、靜平臺的6個球鉸S和6個虎克鉸U中心分別布置在兩個平面之中。為了方便分析，選擇絕對靜坐標系Obxyz與靜平臺固連，相對動坐標系Oaαβγ與動平臺固連，其中，Oa、Ob分別是動、靜平臺的外接圓圓心；z、γ軸分別垂直于各自所在平面。動、靜平臺6對頂點Ai、Bi(i=1,2，…，6)分別循環對稱布置在一個平面圓周上，如圖2所示。

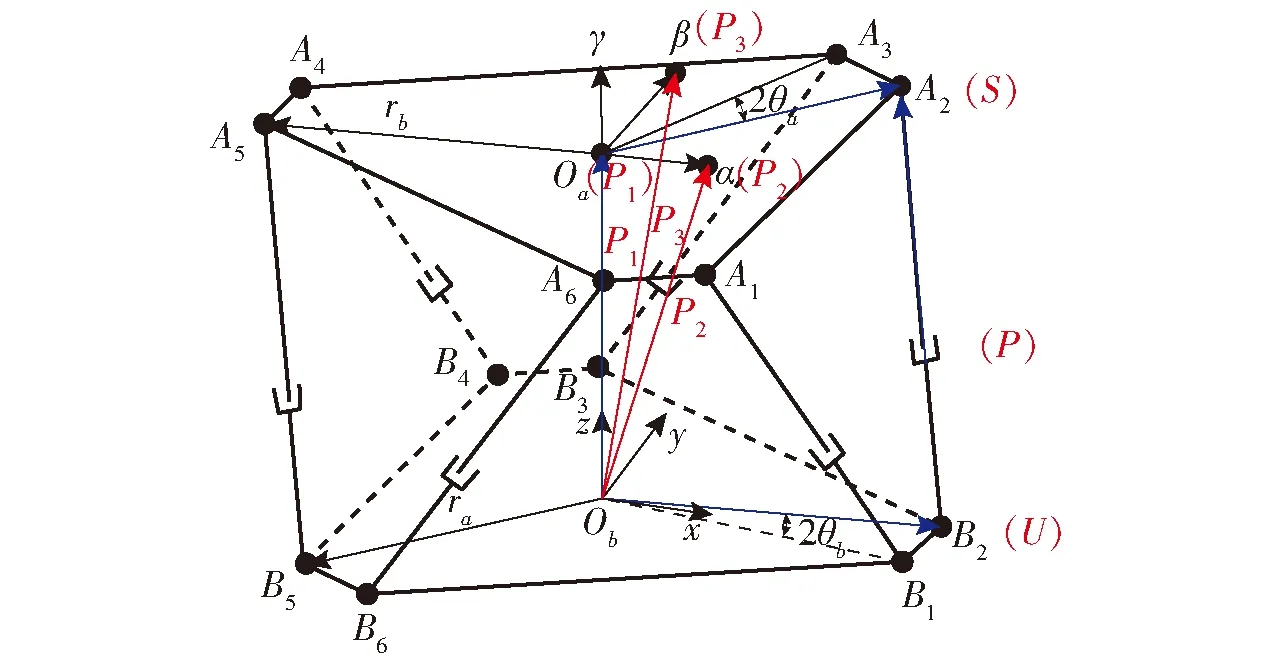
圖1 6-UPS并聯機器人簡圖Fig.1 Structure diagram of 6-UPS parallel robot

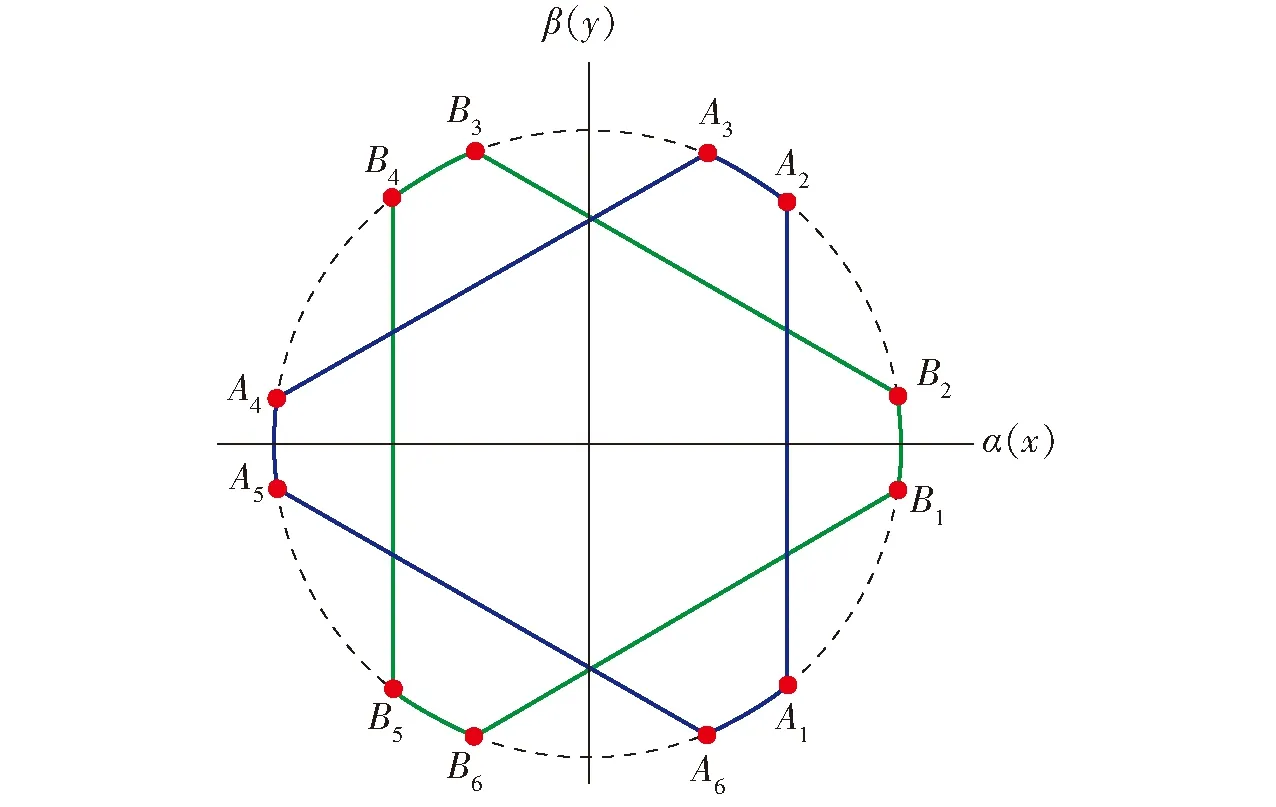
圖2 6-UPS并聯機器人的頂點布置示意圖Fig.2 Vertices arrangement schematic of 6-UPS parallel robot

選擇3點P1、P2、P3為代表點，分別位于動坐標系原點Oa、α軸端點和β軸的端點處，如圖1所示。用P1=(x1,y1,z1)T、P2=(x2,y2,z2)T、P3=(x3,y3,z3)T分別表示3個代表點P1、P2、P3在靜坐標系Obxyz中的位置坐標，于是正向運動學模型中含有9個待求變量。

1.2 基于代表點坐標的位置P和姿態R

P2、P3和P1存在如下關系：P2=P1+R·x，P3=P1+R·y。動平臺動坐標系Oaαβγ的α、β、γ軸對應的矢量記為：α=(αx,αy,αz)T，β=(βx,βy,βz)T，γ=(γx,γy,γz)T。則矢量α、β、γ用代表點P1、P2、P3坐標表示后可得

α=P2-P1=(x2,y2,z2)T-(x1,y1,z1)T= ((x2-x1),(y2-y1),(z2-z1))T

(1)

同理可得

β=((x3-x1),(y3-y1),(z3-z1))T

(2)

由于γ垂直于α和β所決定的平面，所以存在

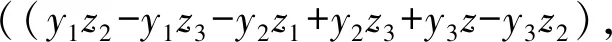
(3)

靜坐標系基矢量為：x=(1,0,0)T；y=(0,1,0)T；z=(0,0,1)T。采用代表點表示，動平臺位置在靜坐標系中的位置矢量為P=P1=(x1,y1,z1)T；姿態矩陣R表示為

(4)

根據式(1)～(3)可得αx=x2-x1、αy=y2-y1、αz=z2-z1、βx=x3-x1、βy=y3-y1、βz=z3-z1、γx=y1z2-y1z3-y2z1+y2z3+y3z1-y3z2、γy=-x1z2+x1z3+x2z1-x2z3-x3z1+x3z2、γz=x1y2-x1y3-x2y1+x2y3+x3y1-x3y2。

2 6-UPS并聯機器人位置矢量方程構建

Lkek=P+Rak-bk(k=1,2，…,6)

(5)

其中

ak=(akα,akβ,akγ)T

bk=(bkx,bky,bkz)T

式中Lk——第k個連桿桿長

ek——第k個連桿單位矢量

ak——動坐標系Oaαβγ中動平臺各個頂點Ak坐標值

bk——靜坐標系Obxyz中靜平臺各個頂點Bk坐標值

圖1所示機構，因動、靜平臺均為平面布置，所以ak、bk的γ軸和z軸分量均為0，即akγ=bkz=0，也即ak=(akα,akβ,0)T，bk=(bkx,bky,0)T，可見動、靜平臺的頂點坐標也可以通過4個變量ra、rb、θa、θb來表示，各點坐標進一步表示如下

(6)

其中

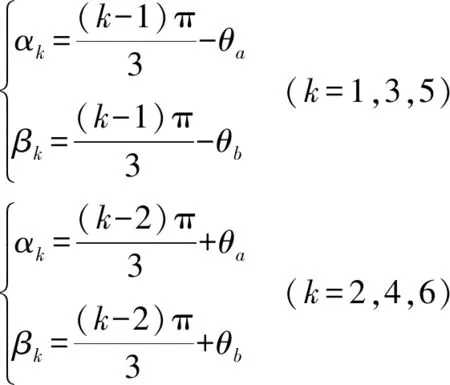
令W為動平臺在動坐標系中的位置矢量，W=(Wx,Wy,Wz)T，則存在P=RW，結合R的正交性，同時成立：W=RTP。將ak、bk、P、R和W代入式(5)，兩邊與自身進行矢量點乘，得到6個桿長平方標量方程式如下(此處省略下標k)

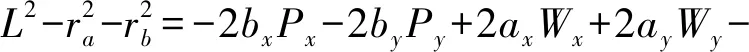
(7)

其中Px=P·xPy=P·yWx=P·αWy=P·β

αx=α·xαy=α·yβx=β·xβy=β·y

式中Pp——位置矢量P模長平方

Px——P在x方向上的投影

Py——P在y方向上的投影

Wx——P在α方向上的投影

Wy——P在β方向上的投影

αx——α在x方向上的投影

αy——α在y方向上的投影

βx——β在x方向上的投影

βy——β在y方向上的投影

式中，含Pp、Px、Py、Wx、Wy、αx、αy、βx、βy等9個未知數，各個未知數之間由動平臺的位置和姿態各個參數聯系起來，且9個未知數的系數由平臺結構參數和桿長參數決定。

3 正向運動學模型構造并求解

正向運動學問題就是已知機構的6個桿長輸入，求解末端運動平臺的位置矢量P和姿態矩陣R。此處首先將正向運動學問題轉換為構造和求解6個二次多項式方程問題。

3.1 運動學模型構造

由式(7)可得，通過對Pp、Px、Py、Wx、Wy、αx、αy、βx、βy9個未知數進行移項、整理，可解得

(8)

其中

(9)

將9個未知數的代表點表達式代入式(8)后可得6個一次或二次多項式方程組

(10)

(11)

(12)

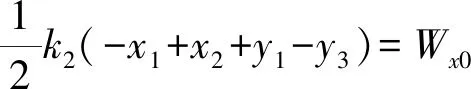
(13)

(14)

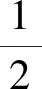
(15)

又由α和β的正交性和歸一性

α·β=0α·α=1β·β=1

可得9個未知數的代表點約束方程

(x2-x1)(x3-x1)+(y2-y1)(y3-y1)+ (z2-z1)(z3-z1)=0

(16)

(x2-x1)2+(y2-y1)2+(z2-z1)2=1

(17)

(x3-x1)2+(y3-y1)2+(z3-z1)2=1

(18)

觀察式(11)、(12)、(15)最高次為一次多項式，本文先求出x3、y2、y3對x1、y1、z1、x2、z2、z3的線性表示，再代回剩余的6個方程，可得到式(10)、(13)、(14)、(16)～(18)的6個二次多項式方程，將其記為

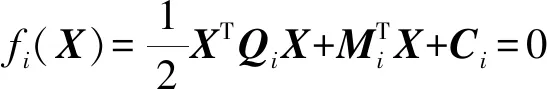
(19)

其中X為待求未知數，X=(x1,y1,z1,x2,z2,z3)，Ci是由6-UPS并聯機器人結構參數和6條支腿長決定；Mi由6-UPS并聯機器人結構參數所決定；Qi(i=1,2,…,6)是二次項系數矩陣，是由系統結構參數中3個參數ra、θa、θb所決定的6×6維對稱矩陣，Qi的具體形式為

將式(19)代表的6個方程統一表示為向量形式

(20)

其中F(X)=(f1(X),f2(X),…,f6(X))T

Q=(Q1,Q2,…,Q6)TM=(M1,M2,…,M6)TC=(C1,C2,…,C6)T

(21)

(22)

3.2 正解運動學方程數值迭代求解

對二次多項式方程組(20)求導，可得

現在考慮牛頓-拉夫森數值迭代算法，當待求未知變量X取第k步數值，即：X=xk時，可得

因此可得

(23)

根據一般牛頓-拉夫森數值迭代算法

(24)

將式(23)代入X=xk時的方程組(20)可得

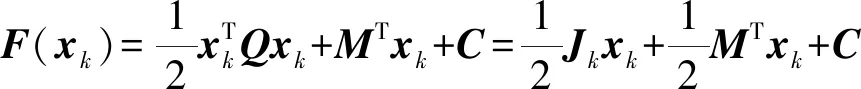
(25)

將式(25)代回式(24)一般牛頓-拉夫森數值迭代算法可得

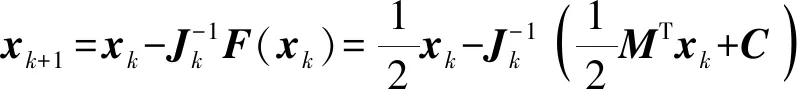
(26)

(27)

由式(26)和式(27)聯合可得一類代表點表示的6-UPS并聯機器人的快速正向運動學迭代算法

(28)

據此，可解出唯一一組變量x1、y1、z1、x2、z2、z3的解，根據P=(x1,y1,z1)T和姿態矩陣R(式(4))可以求解出唯一的位置和姿態。

4 數值算例驗證

采用數值算例來說明和驗證前文方法的正確性、高效性。

(1)正確性

通過給定一組反解，即給定平臺位置姿態，計算對應的代表點坐標值。將給定的一組初始代表點坐標值代入式(28)進行運動學正解計算，如果能夠收斂、且收斂到反解對應的代表點坐標值，即可驗證所提算法的正確性。

① 給定反解條件。6-UPS并聯機器人結構參數θa=0.286 18π、θb=0.046 988π、ra=0.849 864、rb=0.849 864，由此可以確定6-UPS并聯機器人動、靜平臺的頂點坐標ai、bi(i=1，2，…，6)。角度單位為rad，長度單位為m。設定6-UPS并聯機器人預設狀態下位置矢量為Pt=(-0.2,-0.03,1.1)T，姿態矩陣Rt為

可得到P1=(-0.2,-0.03,1.1)T，通過P2=P1+Rt(1,0,0)T，P3=P1+Rt(0,1,0)T計算可得另外兩個代表點坐標分別為：P2=(0.769 017，-0.194 971,1.283 82)T，P3=(-0.028 091 9，0.954 859,1.077 65)T，通過反解計算得到6條支腿長為：L1=1.516 92 m、L2=1.318 95 m、L3=1.268 81 m、L4=1.136 69 m、L5=1.257 04 m、L6=1.209 43 m。

根據課題組研制的物理樣機，其構型選擇的電缸行程為0.5 m，6條支腿的平衡位置均在1.36 m處，即6條支腿的運動范圍均在(1.360.25) m范圍內，即：關節空間范圍為Li∈[1.11,1.61]，i=1,2,…,6，進而可以驗證Pt、Rt選取正確。

② 求解正解。首先，將6-UPS并聯機器人結構參數和腿長參數代入前述的C、M、Q，可得

假設6-UPS并聯機器人動平臺從初始位姿：P0=(0.5,0.5,2)T，R0=I3×3出發，運動到反解給定的位姿：Pt、Rt。那么，對應的始末位姿代表點坐標值分別為：X0=(0.5,0.5,2,1.5,2,2)T、Xt=(-0.2,-0.03,1.1,0.769 017,1.283 82,1.077 65)T。

迭代過程如表1所示，經過5次迭代計算后得到的X5=(-0.2,-0.03,1.1,0.769 017,1.283 82,1.077 65)T與反解給定的Xt=(-0.2,-0.03,1.1,0.769 017,1.283 82,1.077 65)T完全一致，驗證了所提算法是正確的，機構位姿示意如圖3所示。

本次計算中，所提方法迭代時間為0.20 ms，對比計算表明，采用傳統歐拉角方法描述的牛頓-拉夫森方法，則迭代次數8次、需要耗時2.67 ms，由此可見本文所提出的二次形方程組數值迭代方法的迭代次數少，用時少，收斂速度快，效率提高92.51%，至此，初步顯示出算法的高效性。

(2) 高效性

與旋轉矩陣方法的計算進行對比，即可驗證所提算法的高效性。所提算法和旋轉矩陣方法均在以下條件下進行計算，計算機硬件為：Win 8.1/Intel Core i5 2.4 GHz/8 GB RAM/MatlabR2016b，代表點初始值取X0=(0.5,0.5,2,1.5,2,2)T，最大迭代次數均為20次，算法終止條件允許誤差‖Δx‖<10-8。

表1 迭代過程及其結果Tab.1 Iterative process and results

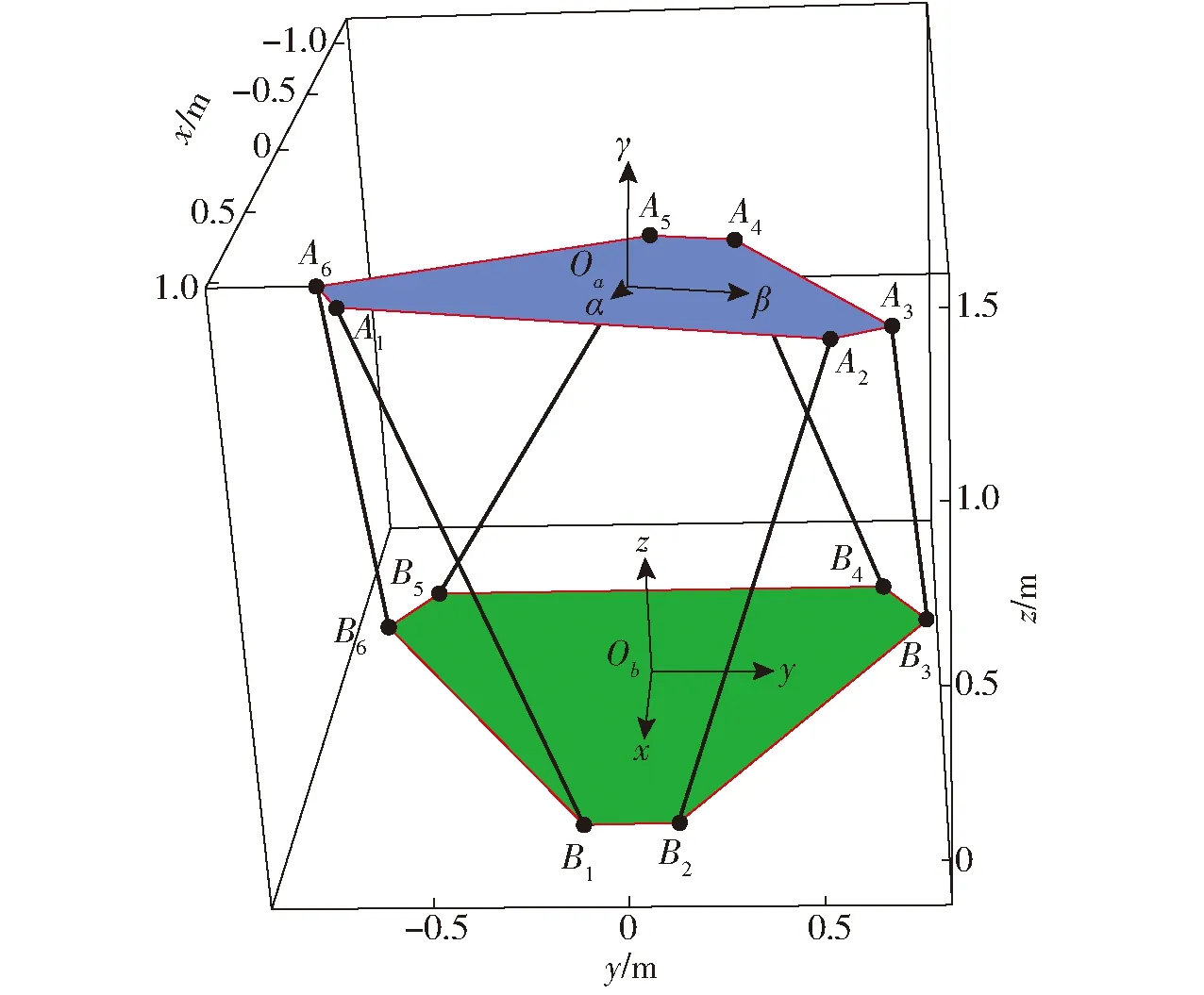
圖3 位置和姿態示意圖Fig.3 Schematic of position and orientation for 6-UPS parallel robot

為了進一步驗證所提算法的高計算效率，根據課題組研制的物理樣機，在其可達無奇異工作空間內任意選取25組數據。首先，25組初始位置姿態P0i、R0i均取為P0、R0，其具體數值為：P0=(0.5,0.5,2)T，R0=I3×3，轉換成代表點表示為：X0=(0.5,0.5,2,1.5,2,2)T。其次，針對表2中給定的25組數據，其每一組數據均是從初始位姿：P0、R0開始，分別代入所提算法，重復(1)的反解、正解過程并進行計算，動平臺最終分別運動到表2中給定的25組終止位置姿態，即25組Pti、Rti處。經過計算可知，25組數據計算結果均正確且收斂，同時也得到每一組數據計算所需時間，并將其與旋轉矩陣方法計算反解、正解過程所需時間進行對比。每一組位姿在Matlab中計算100次并取平均數值即為本次計算時間，結果如表2所示。

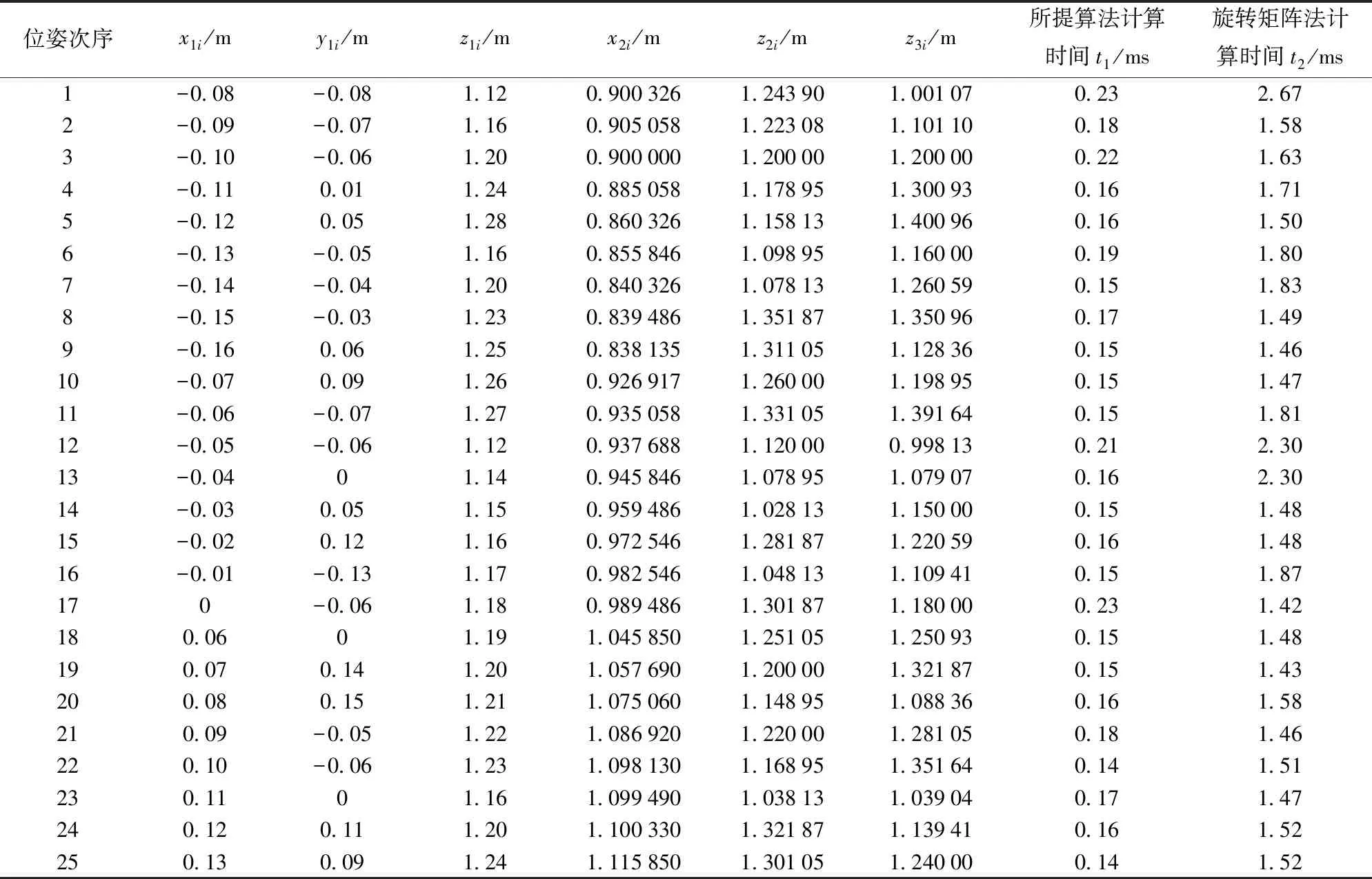
表2 兩種算法計算時間對比Tab.2 Consumption time comparison of two algorithms

5 結論

(1)采用代表點描述可將并聯機器人正向運動學模型表達為一組二次方程組。該模型含有二次項、一次項和常數項，最高次項為二次，求導后得到的雅可比矩陣僅含有一次項和常數項，最高次項為一次，建立了簡單非線性的并聯機器人正向運動學模型。

(2)結合正運動學模型的特點，對一般的牛頓-拉夫森方法進行改進，改進后的牛頓-拉夫森迭代方法不需要求解雅可比的逆矩陣；而且，在每一次迭代計算過程中，部分變量還原到原始二次形，計算過程中直接抵消了大部分計算，方程組與雅可比矩陣的更新僅需消耗極少的計算量，由此確保所提算法收斂速度快、計算效率高，并可得到唯一解，便于實時控制所需。

(3)通過對比傳統的旋轉矩陣方法，本文提出的二次方程組數值迭代方法的迭代次數少、用時少、收斂速度快，效率高。