斷裂能與統(tǒng)一損傷加載面描述的混凝土本構(gòu)模型

何偉，谷鈺，徐穎

?

斷裂能與統(tǒng)一損傷加載面描述的混凝土本構(gòu)模型

何偉，谷鈺，徐穎

(安徽理工大學(xué) 土木建筑學(xué)院，安徽 淮南 232001)

構(gòu)建一個混凝土損傷本構(gòu)模型，研究目的為解決現(xiàn)有模型中存在的損傷演化、雙軸強(qiáng)度與網(wǎng)格尺寸依賴性問題。基于試驗觀察，提出符合實(shí)際的壓縮損傷演化方程；在不可逆熱力學(xué)的框架下，利用當(dāng)量轉(zhuǎn)化應(yīng)力狀態(tài)的方法，在應(yīng)變空間構(gòu)造統(tǒng)一損傷加載面，以表達(dá)混凝土的雙軸強(qiáng)度；借助斷裂能對損傷閥值正則化的方法，以合理反映應(yīng)變軟化過程中的能量耗散，并達(dá)到消除網(wǎng)格尺寸依賴性之目的。采用編制的程序，對單軸與雙軸加載、四點(diǎn)彎非比例加載等混凝土試驗進(jìn)行數(shù)值計算，驗證了模型的合理性與有效性。研究結(jié)果表明：模型不僅解決了上述存在的問題，而且具備在較復(fù)雜應(yīng)力路徑下預(yù)測結(jié)構(gòu)的承載力、變形及裂縫擴(kuò)展的能力，可為混凝土結(jié)構(gòu)的定量評價提供支持依據(jù)。

損傷演化；雙軸強(qiáng)度；網(wǎng)格尺寸依賴性；當(dāng)量轉(zhuǎn)化；損傷加載面；斷裂能；應(yīng)變軟化

數(shù)值計算，與理論分析和試驗研究相并列，是解決混凝土結(jié)構(gòu)問題的第3種科學(xué)方法。本構(gòu)模型是數(shù)值計算的關(guān)鍵部分，因此，其研究具有重要的理論與工程意義。由于能解釋混凝土因微裂縫的演變所誘致的非線性物理機(jī)制[1]，標(biāo)量損傷本構(gòu)模 型[2?4]被廣泛應(yīng)用于非線性結(jié)構(gòu)分析，但仍存在以下問題。其一，普遍應(yīng)用的Mazars壓縮損傷演化方程[4]，不足以表達(dá)高壓縮應(yīng)變水平下的混凝土行為。其二，應(yīng)力驅(qū)動的損傷模型[5]，難以區(qū)分因應(yīng)變軟化和因卸載引起的應(yīng)力減小力學(xué)機(jī)制，即材料分別處于上述2類狀態(tài)時，應(yīng)力增量均指向損傷加載面內(nèi)部；應(yīng)變驅(qū)動的損傷模型[6?10]，能解決前述問題，卻無法有效描述混凝土在雙軸應(yīng)力狀態(tài)下的強(qiáng)度特征，因而也不能反映結(jié)構(gòu)的實(shí)際工作狀態(tài)。其三，傳統(tǒng)理論框架下的損傷模型[6]，不僅在物理上無法表達(dá)應(yīng)變軟化過程中的能量耗散機(jī)制，而且在數(shù)值結(jié)果上存在網(wǎng)格尺寸依賴性[11](mesh-size dependency)：當(dāng)單元尺寸趨向0時(對應(yīng)于離散已知域的單元數(shù)量趨向無窮大)，材料的破壞趨向零能量耗散，這顯然違背了物理事實(shí)。需要指出，這里的網(wǎng)格尺寸依賴性問題，與通常意義上的單元尺寸影響計算精度問題，存在本質(zhì)的區(qū)別，前者源自應(yīng)變軟化誘致的物理控制方程的類型改變，后者則源于有限元空間離散誤差和插值誤差。網(wǎng)格尺寸依賴性的存在，削弱了損傷模型的物理意義與預(yù)測價值。針對以上問題，本文提出了符合混凝土實(shí)際力學(xué)響應(yīng)的壓縮損傷演化方程；從不可逆熱力學(xué)基本定律出發(fā)，在應(yīng)變空間構(gòu)造統(tǒng)一損傷加載面，演繹出本構(gòu)的全部方程，摒棄有爭議的應(yīng)變等效、能量等效等唯象學(xué)建模假定；注意到應(yīng)力狀態(tài)是混凝土強(qiáng)度的主控力學(xué)機(jī)制這一事實(shí)，利用當(dāng)量轉(zhuǎn)化應(yīng)力狀態(tài)的方法，來表達(dá)混凝土的雙軸強(qiáng)度；借助斷裂能正則化，以達(dá)到緩解網(wǎng)格尺寸依賴性之目的。通過與現(xiàn)有模型及試驗結(jié)果的對比，驗證了建議模型的合理性與有效性。

1 模型構(gòu)建

1.1 熱力學(xué)框架

在率無關(guān)、小應(yīng)變和等溫條件下，設(shè)受損混凝土的Helmholtz自由能為

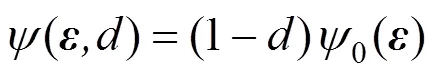
式中：為二階應(yīng)變張量；為標(biāo)量損傷變量；0()為無損混凝土的自由能，定義為

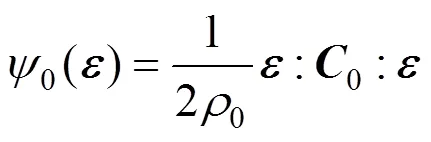
式中：0為材料的質(zhì)量密度，設(shè)為常量；0為無損混凝土的四階彈性剛度張量；“：”為張量縮并運(yùn) 算符。

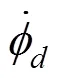
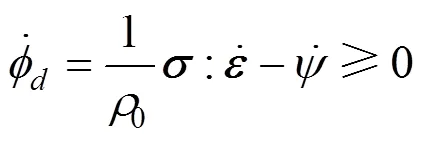
式中：為二階應(yīng)力張量。

將式(1)對時間微分，代入式(3)，由此得

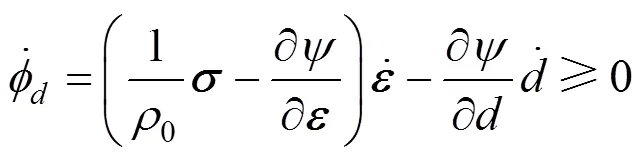
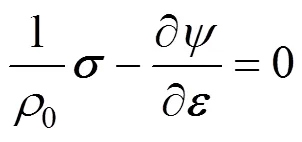
對式(1)求的偏導(dǎo)，代入式(5)，并利用式(2)，于是可導(dǎo)出材料的本構(gòu)方程為

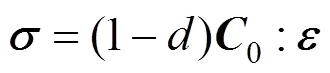
考慮到式(5)和式(1)，式(4)可進(jìn)一步寫為

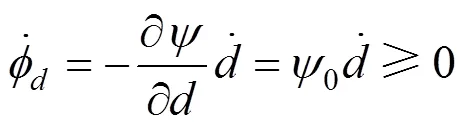
式(7)表明，只要損傷變量在損傷發(fā)展過程中是單調(diào)增加的，即能保證以式(6)表達(dá)的本構(gòu)方程滿足熱力學(xué)第二定律。

1.2 損傷加載面

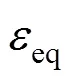
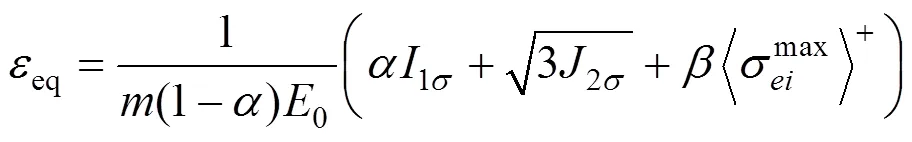
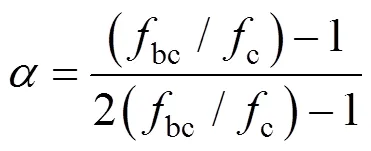
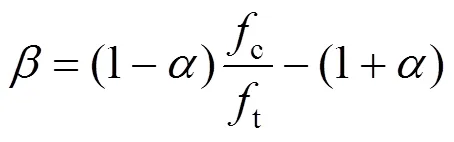
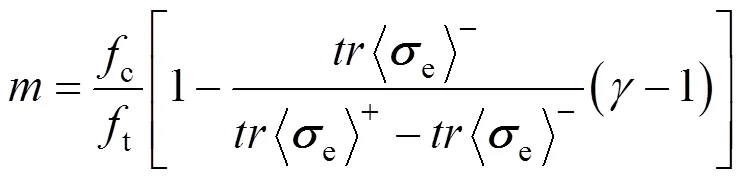
至此，定義應(yīng)變空間下的統(tǒng)一損傷加載面為

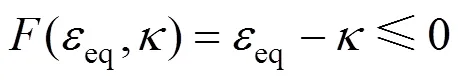
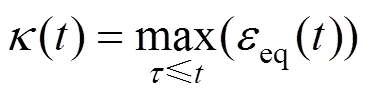
作為式(12)的一個特例，初始損傷加載面0為

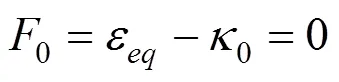
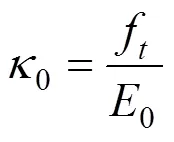
需要指出，式(14)實(shí)質(zhì)上是在應(yīng)變空間定義了材料的極限強(qiáng)度面。

1.3 損傷演化

為刻畫拉壓力學(xué)響應(yīng)迥異的混凝土行為，將損傷變量以拉伸損傷變量t和壓縮損傷變量c的加權(quán)之和[4]來表達(dá)

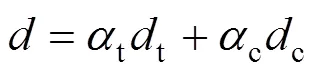
這里，t與c分別為

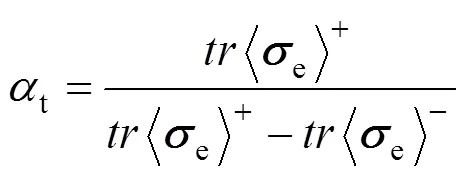
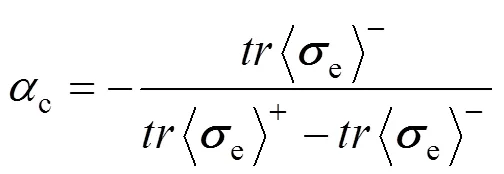
t采用指數(shù)演化規(guī)律[8]：

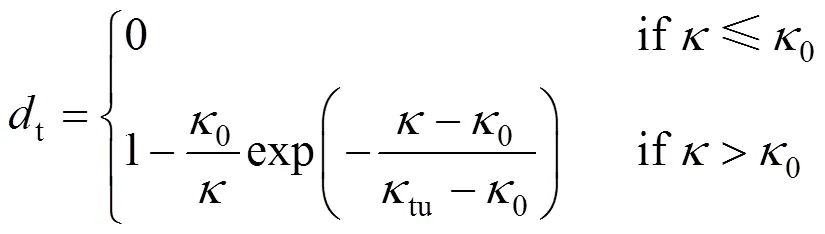
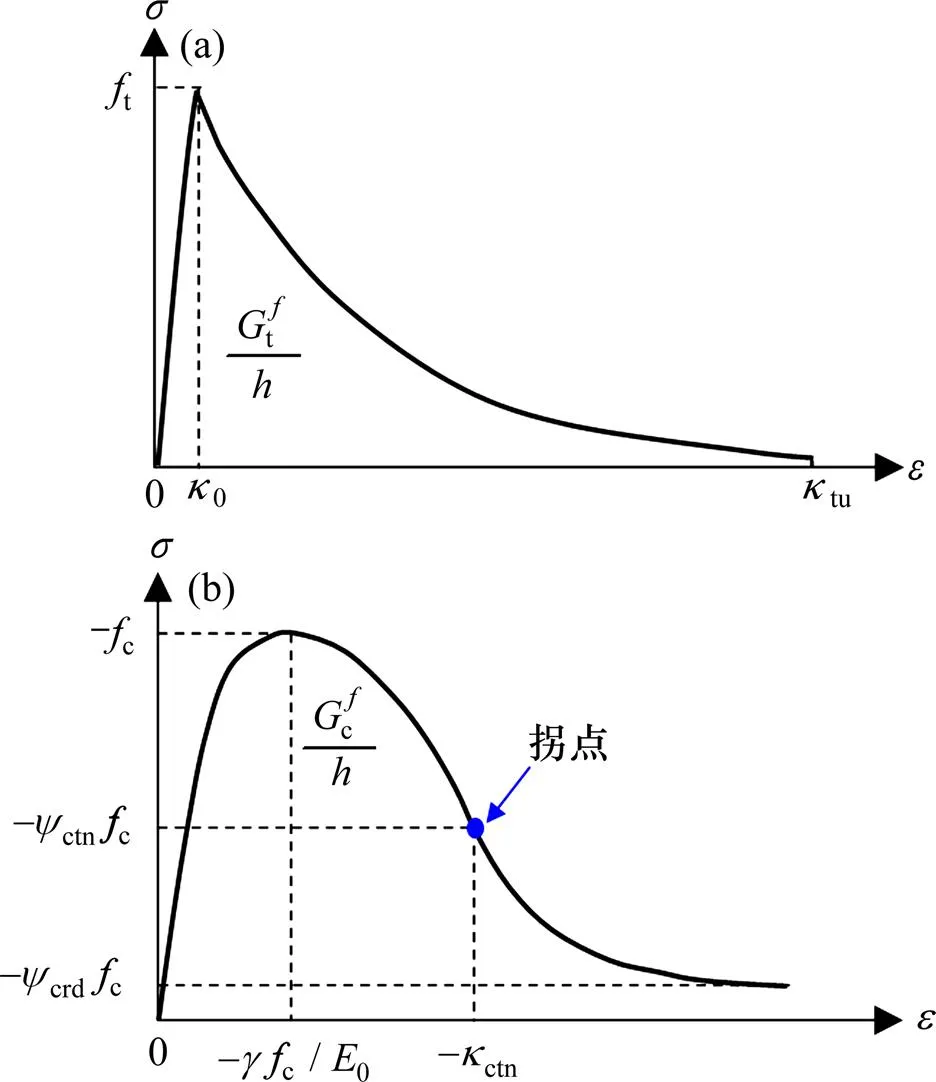
(a) 單軸拉伸；(b) 單軸壓縮

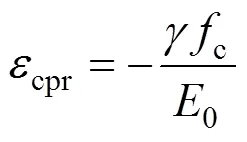
為方便比較，現(xiàn)給出廣泛應(yīng)用的Mazars壓縮損傷演化方程[4]：

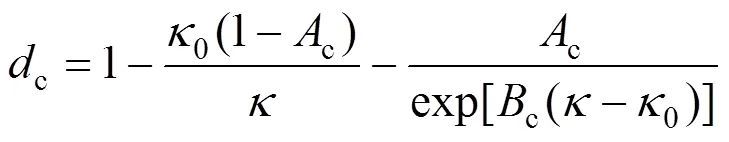
式中：c與c為控制壓縮應(yīng)力–應(yīng)變曲線形狀的材料常數(shù)。

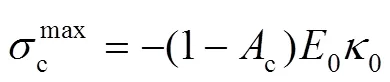
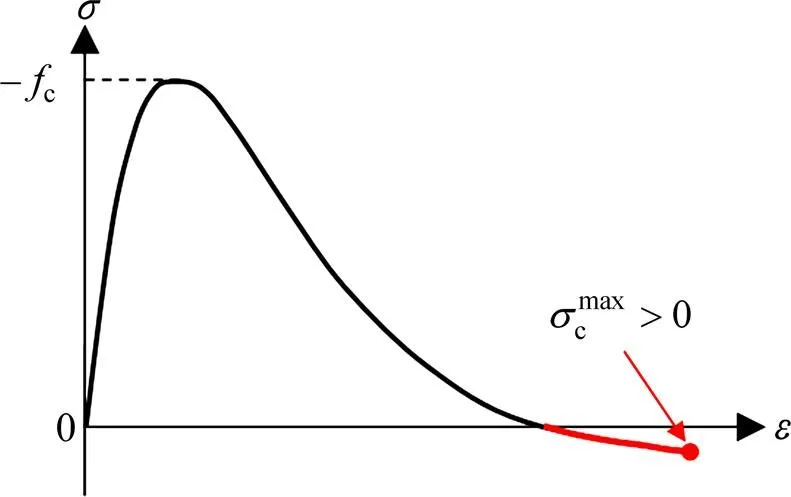
圖2 Mazars的單軸壓縮應(yīng)力?應(yīng)變關(guān)系

1.4 斷裂能正則化

斷裂帶理論[11](Crack band theory)通過斷裂能描述準(zhǔn)脆性材料斷裂過程中的能量耗散，其基本思想是根據(jù)單元尺寸，調(diào)整應(yīng)力–應(yīng)變曲線的軟化段，以保證每單位面積內(nèi)產(chǎn)生一條連續(xù)裂縫所需的能量保持一致，從而達(dá)到消除網(wǎng)格尺寸依賴性之目的。該理論在本構(gòu)層面上的應(yīng)用，又常被稱為斷裂能正則化。

不失一般性，考慮材料處于單軸受拉應(yīng)力狀態(tài)，即

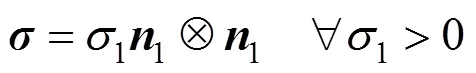
利用式(8)與式(13)，可寫出

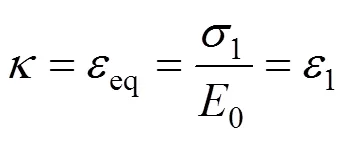
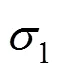
根據(jù)斷裂帶理論[11]，存在以下關(guān)系：

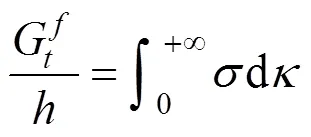
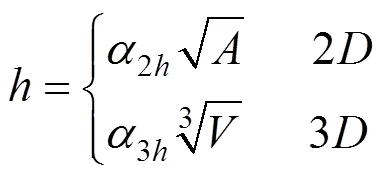
式(24)的物理意義見圖1(a)。

將式(6)代入式(24)，并考慮到式(19)與式(23)，從而得到

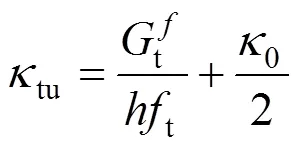
類似地，在單軸壓縮應(yīng)力狀態(tài)下，重復(fù)以上過程，有以下關(guān)系式：

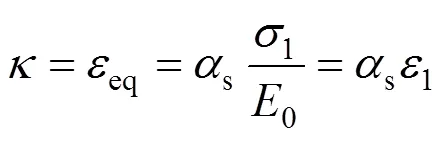
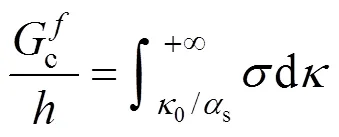
式(28)的物理意義見圖1(b)。

2 模型驗證

根據(jù)建議的本構(gòu)模型，編制相應(yīng)的程序，對若干經(jīng)典混凝土試驗[13?16]進(jìn)行有限元計算，并和試驗結(jié)果進(jìn)行比較，以驗證模型的合理性與有效性。各驗證算例的混凝土材料參數(shù)見表1。另外，除非特別指明，各算例所用單元均為四節(jié)點(diǎn)四邊形平面應(yīng)力等參單元，計算結(jié)果分述如下。

2.1 單軸加載

為在材料層次上驗證模型的準(zhǔn)確性并探討模型在二維與三維情況下的適用性，對混凝土試件的單軸拉伸[13]與單軸壓縮[14]試驗進(jìn)行數(shù)值計算。所用單元分別為二維四節(jié)點(diǎn)四邊形平面應(yīng)力單元與三維八節(jié)點(diǎn)六面體實(shí)體單元。由圖3可見，計算值與試驗值吻合較好，反映模型可以準(zhǔn)確地再現(xiàn)混凝土在單軸加載條件下的應(yīng)力與應(yīng)變特征；而且，計算結(jié)果也表明建議模型適用于三維計算。

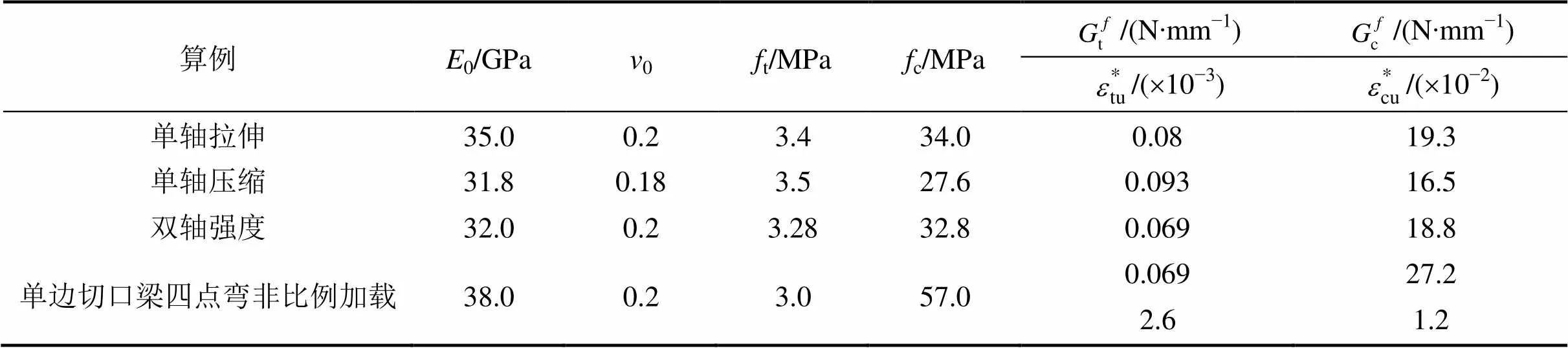
表1 算例的材料參數(shù)

注*：tu與cu分別為單軸拉伸與單軸壓縮極限應(yīng)變，為傳統(tǒng)模型的材料參數(shù)，用于單邊切口梁四點(diǎn)彎非比例加載的數(shù)值分析

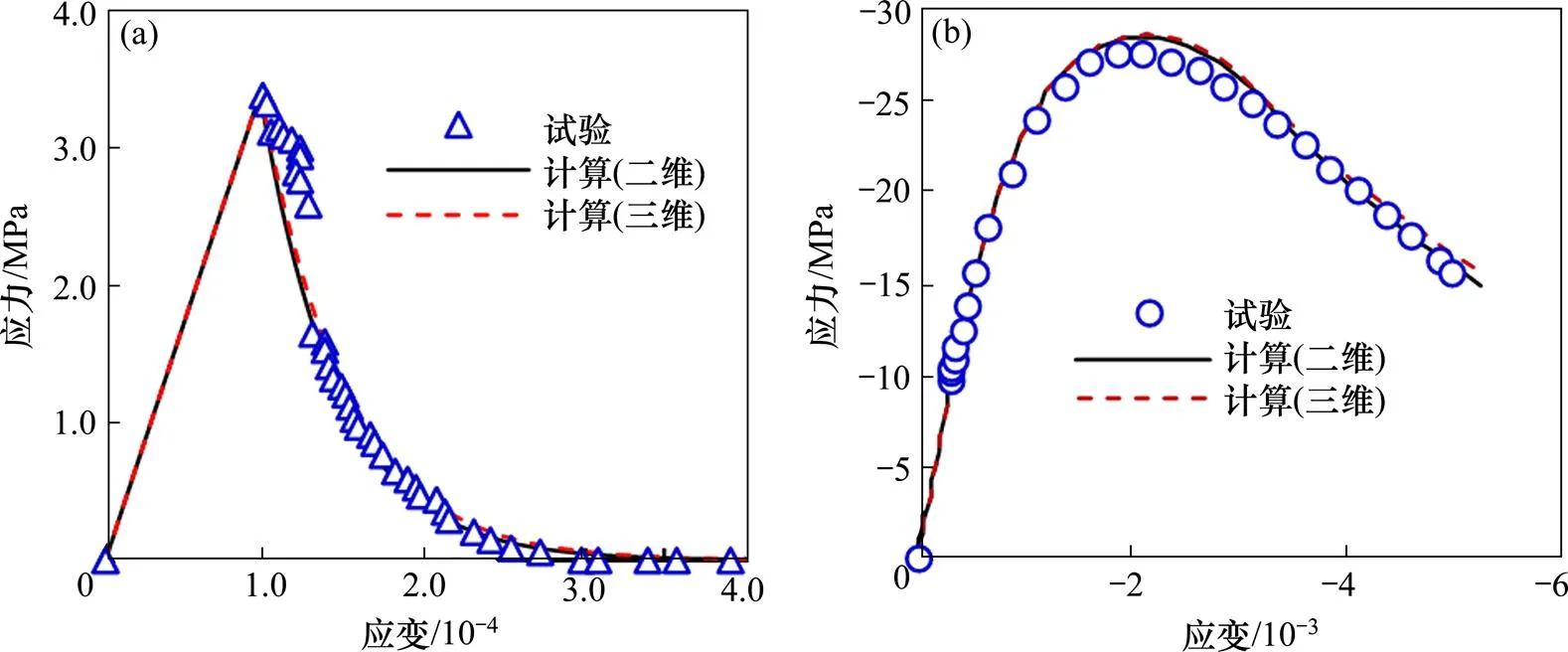
(a) 單軸拉伸；(b) 單軸壓縮

2.2 雙軸強(qiáng)度

為檢驗和比較現(xiàn)有模型與建議模型對混凝土雙軸強(qiáng)度的表征能力，對Kupfer的混凝土雙軸強(qiáng)度試驗[15]進(jìn)行數(shù)值模擬。

為方便比較，表2給出了現(xiàn)有文獻(xiàn)中典型當(dāng)量應(yīng)變的表達(dá)式[4, 7?8, 10]。

表2 典型當(dāng)量應(yīng)變的表達(dá)式

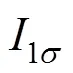
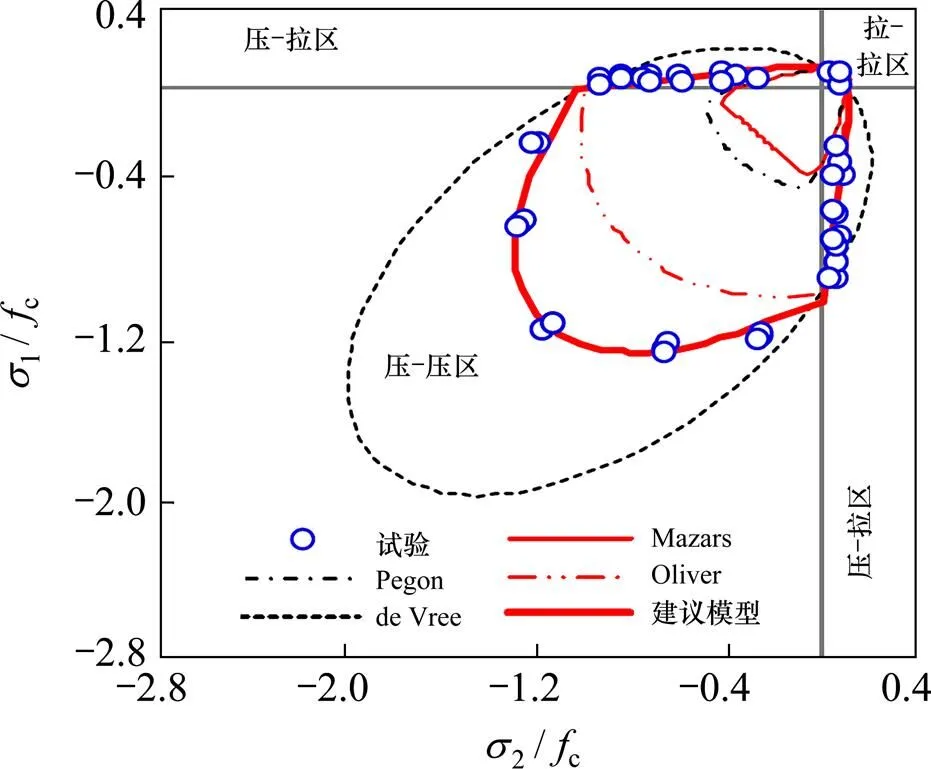
圖4 混凝土雙軸強(qiáng)度包絡(luò)線的比較

2.3 單邊切口梁四點(diǎn)彎非比例加載

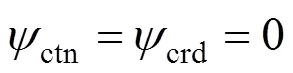
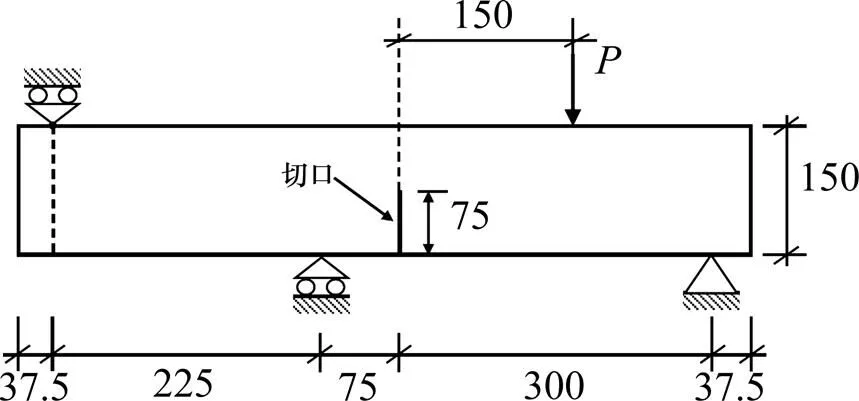
單位：mm

采用3種不同疏密的有限元網(wǎng)格(即粗、中和細(xì)網(wǎng)格)對結(jié)構(gòu)進(jìn)行離散，對應(yīng)的單元數(shù)分別為1 445，2 060和4 090個，網(wǎng)格加密區(qū)的最小單元尺寸分別為5 mm×5 mm，3.75 mm×3.75 mm和2.5 mm×2.5 mm，如圖6所示。

從圖7(a)可見，傳統(tǒng)模型的計算結(jié)果存在顯著的網(wǎng)格尺寸依賴性，即當(dāng)單元尺寸足夠小時，計算結(jié)果并不收斂于試驗上的物理意義解；相反，圖7(b)則表明建議模型在很大程度上消除了網(wǎng)格尺寸依賴性，在不同疏密網(wǎng)格下得到了相當(dāng)一致的計算結(jié)果。

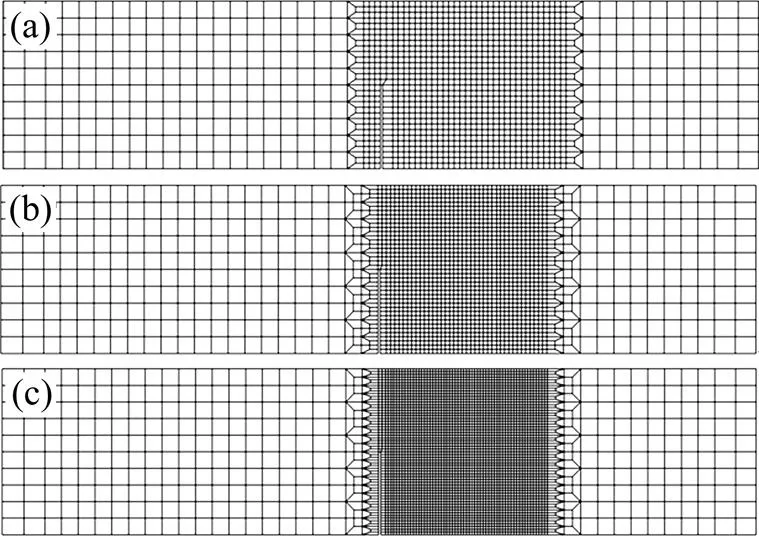
(a) 粗網(wǎng)格；(b) 中網(wǎng)格；(c) 細(xì)網(wǎng)格

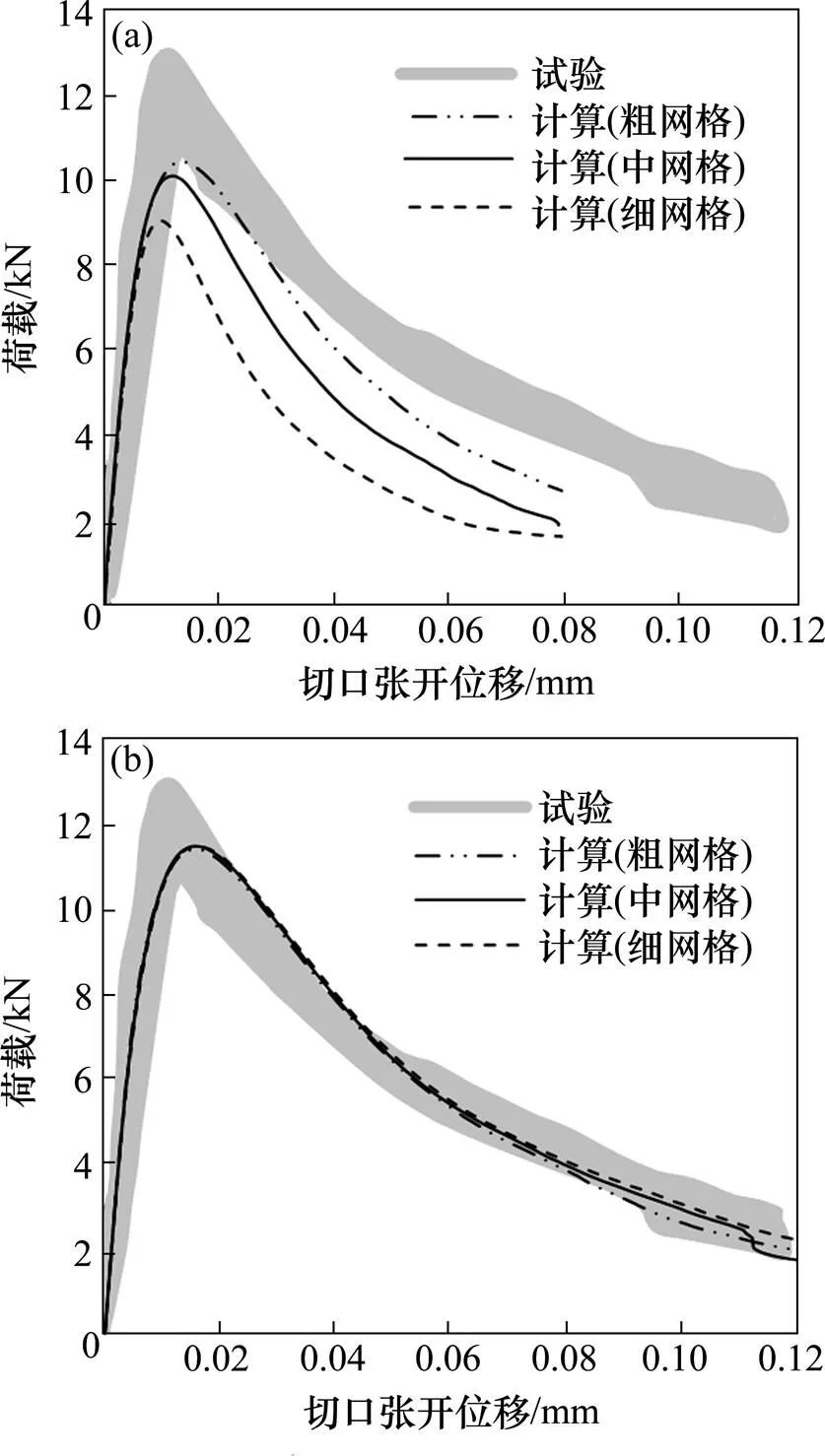
(a) 傳統(tǒng)模型；(b) 建議模型

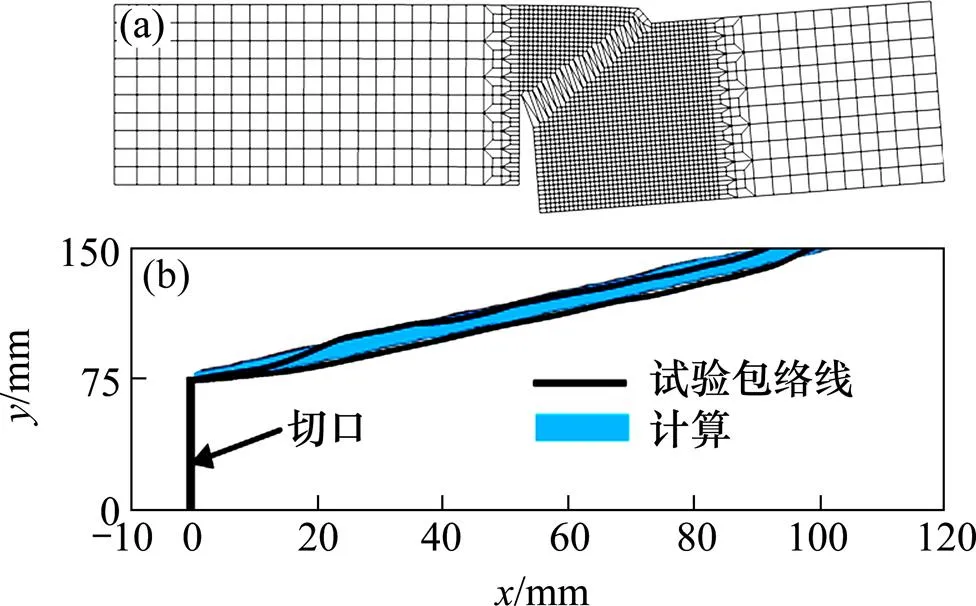
(a) 結(jié)構(gòu)變形(節(jié)點(diǎn)位移放大100倍)；(b) 裂縫擴(kuò)展路徑

因在不同疏密網(wǎng)格下根據(jù)建議模型得到的數(shù)值模擬結(jié)果較為一致，故此處僅給出在中網(wǎng)格下得到的最終結(jié)構(gòu)變形與裂縫擴(kuò)展路徑。圖8(a)清晰地表明，切口區(qū)域的變形特征為在橫、豎向上均有位移，表明結(jié)構(gòu)的破壞是混合型開裂(Mixed Mode Fracture)，與試驗觀察[16]一致；圖8(b)則顯示了計算與試驗得到的裂縫擴(kuò)展路徑十分吻合。

3 結(jié)論

1) 模型解決了當(dāng)前基于應(yīng)變驅(qū)動的混凝土損傷本構(gòu)中存在的問題，即壓縮損傷演化、雙軸強(qiáng)度與網(wǎng)格尺寸依賴性問題。通過對以上問題的解決，進(jìn)一步增強(qiáng)了混凝土損傷本構(gòu)模型的物理意義，提高了其預(yù)測價值。

2) 文中建議的統(tǒng)一損傷加載面不僅有直接的應(yīng)用價值，如可用于混凝土彌散式開裂模型，而且其構(gòu)造思路也可為發(fā)展其他準(zhǔn)脆性材料的極限強(qiáng)度面提供借鑒。

3) 在材料層次上，模型能較全面地刻畫混凝土的主要力學(xué)特性：拉壓力學(xué)響應(yīng)迥異、應(yīng)變軟化與剛度退化。在結(jié)構(gòu)層次上，模型具備了在較復(fù)雜應(yīng)力路徑下預(yù)測結(jié)構(gòu)的承載力、變形及裂縫擴(kuò)展的能力。因此，模型可為混凝土結(jié)構(gòu)的工程設(shè)計及性能評價提供定量的支持依據(jù)。

4) 從實(shí)用角度看，模型具有物理內(nèi)涵明確、收斂性較好、參數(shù)較少且可通過常規(guī)試驗加以確定等優(yōu)點(diǎn)，適合于實(shí)際工程結(jié)構(gòu)的大規(guī)模計算，符合理論服務(wù)于工程實(shí)踐的主要宗旨。

[1] 梁詩雪, 李杰, 俞峰. 基于多尺度分析的混凝土隨機(jī)損傷本構(gòu)關(guān)系[J]. 同濟(jì)大學(xué)學(xué)報(自然科學(xué)版), 2017, 45(9): 1249?1257. LIANG Shixue, LI Jie, YU Feng. A multi-scale analysis-based stochastic damage model of concrete[J]. Journal of Tongji University (Natural Science), 2017, 45(9): 1249?1257.

[2] 商懷帥, 楊魯生. 基于損傷理論的混凝土雙軸壓本構(gòu)模型[J]. 中南大學(xué)學(xué)報(自然科學(xué)版), 2013, 44(1): 340? 344. SHANG Huaishuai, YANG Lusheng. Constitutive model of damage of concrete under biaxial compression[J]. Journal of Central South University (Science and Technology), 2013, 44(1): 340?344.

[3] 李忠獻(xiàn), 陳宇, 李寧. 基于材料損傷的鋼筋混凝土構(gòu)件損傷模型[J]. 工程力學(xué), 2014, 31(6): 53?59. LI Zhongxian, CHEN Yu, LI Ning. A damage model for reinforced concrete members based on material damage[J]. Engineering Mechanics, 2014, 31(6): 53?59.

[4] Mazars J, Pijaudier-Cabot G. Continuum damage theory—application to concrete[J]. Journal of Engineering Mechanics, 1989, 115(2): 345?365.

[5] Manzoli O L, Maedo M A, Bitencourt Jr L A G, et al. On the use of finite elements with a high aspect ratio for modeling cracks in quasi-brittle materials[J]. Engineering Fracture Mechanics, 2016, 153: 151?170.

[6] Alam S Y, Loukili A. Transition from energy dissipation to crack openings during continuum-discontinuum fracture of concrete[J]. International Journal of Fracture, 2017, 206(1): 49?66.

[7] Pegon P, Anthoine A. Numerical strategies for solving continuum damage problems with softening: application to the homogenization of masonry[J]. Computers & structures, 1997, 64(1/4): 623?642.

[8] Oliver J, Cervera M, Oller S, et al. Isotropic damage models and smeared crack analysis of concrete[C]// Proceedings of the 2nd International Conference on Computer Aided Analysis and Design of Concrete Structures. Swansea, U.K.: Pineridge Press, 1990: 945? 957.

[9] Juárez-Luna G, Méndez-Martínez H, Ruiz-Sandoval M E. An isotropic damage model to simulate collapse in reinforced concrete elements[J]. Latin American Journal of Solids and Structures, 2014, 11(13): 2444?2459.

[10] De Vree J H P, Brekelmans W A M, Van Gils M A J. Comparison of nonlocal approaches in continuum damage mechanics[J]. Computers & Structures, 1995, 55(4): 581?588.

[11] Ba?ant Z P, Oh B H. Crack band theory for fracture of concrete[J]. Materials and Structures, 1983, 16(3): 155? 177.

[12] 過鎮(zhèn)海. 混凝土的強(qiáng)度和變形: 試驗基礎(chǔ)和本構(gòu)關(guān)系[M]. 北京: 清華大學(xué)出版社, 1997. GUO Zhenhai. Concrete strength and deformation: test basic and constitutive relation[M]. Beijing: Tsinghua University Press, 1997.

[13] 張其云. 混凝土隨機(jī)損傷本構(gòu)關(guān)系研究[D]. 上海: 同濟(jì)大學(xué), 2001. ZHANG Qiyun. Study of stochastic damage constitutive relationship for concrete material[D]. Shanghai: Tongji University, 2001.

[14] Karsan I D, Jirsa J O. Behavior of concrete under compressive loadings[J]. Journal of the Structural Division ASCE, 1969, 95(12): 2543?2563.

[15] Kupfer H, Hilsdorf H K, Rusch H. Behavior of concrete under biaxial stresses[J]. ACI Journal, 1969, 66(8): 656? 666.

[16] Gálvez J C, Elices M, Guinea G V, et al. Mixed mode fracture of concrete under proportional and nonproportional loading[J]. International Journal of Fracture, 1998, 94(3): 267?284.

Concrete constitutive model described by fracture energy and unified damage loading surface

HE Wei, GU Yu, XU Ying

(School of Civil Engineering and Architecture, Anhui University of Science and Technology, Huainan 232001, China)

This paper proposes a concrete damage constitutive model that aims to solve problems of damage evolution, biaxial strength and mesh-size dependency in existing models. Based on the experimental observation, a real compressive damage evolution equation was proposed. In the framework of irreversible thermodynamics, a unified damage loading surface was developed to describe the biaxial strength of concrete by the method of transforming stress states into an equivalent strain. The problem of mesh-size dependency was solved by the fracture energy regularization of damage thresholds, in which the energy dissipation can be evaluated properly during the strain softening. With the application of the user program, the rationality and validity of the model were demonstrated by the numerical calculation of concrete specimens subjected to different loadings, which include uniaxial and biaxial loadings, and the four-point bending with non-proportional loading. The results show that the model not only solves the aforementioned problems, but also has the ability to predict the structural load-carrying capacity, deformation and crack propagation under complex stress paths, and provides a support to the quantitative evaluation of concrete structures.

damage evolution; biaxial strength; mesh-size dependency; equivalent transformation; damage loading surface; fracture energy; strain softening

10.19713/j.cnki.43?1423/u.2019.04.023

TU528

A

1672 ? 7029(2019)04 ? 1008 ? 08

2018?05?10

國家自然科學(xué)基金資助項目(51208005)；安徽理工大學(xué)博士基金資助項目(11084)

何偉(1977–)，男，安徽桐城人，講師，博士，從事土木工程材料的本構(gòu)建模研究；E–mail：whe@aust.edu.cn

(編輯 陽麗霞)