約束于圓弧的路線平面直線段重構算法

彭書航，蒲浩

?

約束于圓弧的路線平面直線段重構算法

彭書航1，蒲浩2, 3

(1. 西北工業大學 航空學院，陜西 西安 710072；2. 中南大學 土木工程學院，湖南 長沙 410075；3. 高速鐵路建造技術國家工程實驗室，湖南 長沙 410075)

提出一種利用一組(,)直角坐標點擬合與給定的圓弧相切的直線的算法。該算法遵循總體最小二乘準則來構建約束于圓弧的擬合直線的數學模型，在分析函數單調隔根區間的基礎上，利用反拉格朗日插值迭代法計算出函數在定義域內的所有數值根，再經最小二乘準則檢驗獲得數學模型的解，即擬合直線的回歸參數。研究結果表明：擬合數學模型簡明，基于單調隔根區間的迭代算法穩健，速度快，效果優，可用于重構路線平面的精確幾何參數。

路線重構；約束直線擬合；總體最小二乘；隔根區間；反拉格朗日迭代

自動駕駛技術是人工智能研究發展的一個重要方向，其實現機理之一是利用導航定位技術來實時測量車輛的坐標，然后與路線平面的曲線數學方程進行匹配驗證，從而決策車輛的運行方向和速度，控制車輛平穩、安全、舒適地運行。根據中華人民共和國國家統計局公布數據，截至2016年，我國道路通車里程達469.63萬km，鐵路通車里程達14.2萬km。其中相當大一部分道路和鐵路因建設于非信息化時代，缺乏準確的路線平面解析數據(曲線數學方程)，不能為自動駕駛提供基礎的信息服務，因此需要通過現代測量手段來測量路線平面上的一系列坐標點，然后擬合出路線平面的曲線數學方程。Casal等[1?9]對路線中線的優化重構方法進行了廣泛研究，它們的共同點是基于所有曲線、直線段均具有同權的擬合結果來構建擬合數學模型。當曲線較長而與其相鄰的直線測點少且密時，測量誤差對直線擬合效果的影響非常明顯，導致其間不能插入合理的緩和曲線，此時宜考慮直線段與曲線段具有不同的擬合權，給予圓弧優先擬合權，直線擬合須與優先擬合的圓弧相切，確保車輛行駛軌跡的連續性。針對這一難點，本文提出一種解算約束于圓弧的直線擬合方法。

1 最小二乘直線擬合

平面直線的最小二乘擬合分為普通最小二乘擬合和總體最小二乘擬合。設直線的回歸方程為：

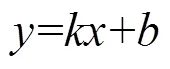
則普通最小二乘擬合的準則是：

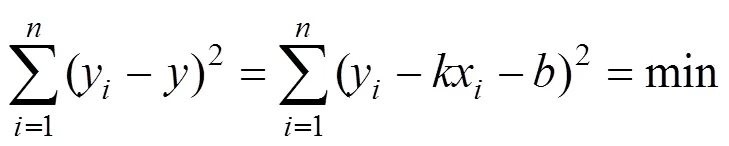
總體最小二乘的準則是：

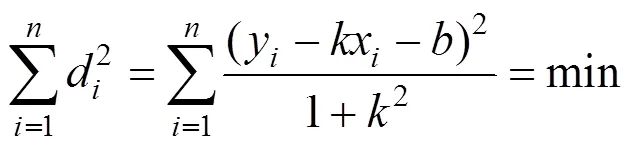
式中：為直線的斜率；為軸的截距；d為測點到擬合直線的垂直距離。和是回歸參數。

普通最小二乘計算過程簡單，但只考慮了自變量的測量誤差，其實質是使因變量坐標差的平方和最小，擬合結果往往不是最優的，直線斜率絕對值越大，擬合結果越差。總體最小二乘是使各測點到擬合直線垂直距離的平方和最小，此準則同時考慮了和變量的測量誤差，可以獲得直線的最佳擬合效果[10]。表1和表2為某企業鐵路專用線上一個直線段RTK測量數據的2種擬合結果(為遵循相關法律，表中坐標數據經過變換處理)。計算結果表明，直線較陡時，總體最小二乘擬合明顯優于普通最小二乘擬合。

因此，本文采用總體最小二乘準側來擬合約束于圓弧的直線。

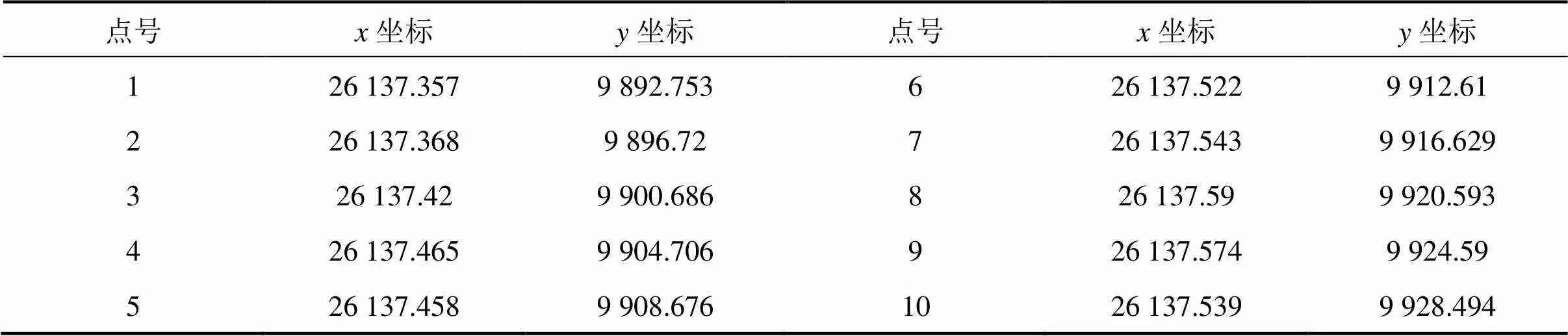
表1 RTK測量數據

表2 2種準則的直線擬合比較

2 擬合數學模型

車輛行駛中線是由若干直線段和圓弧段(可能有過渡緩和曲線)交互相連構成。當直線段短，測點少且密集，不能通過過渡曲線與圓曲線相連時，宜先擬合出圓弧的參數，再擬合與之相連的直線，使直線與圓弧相切。

劉元朋等[11]給出了引入系數約束條件的圓曲線總體最小二乘擬合方法，解決了其他迭代法運算量大和近似算法擬合效果差的問題。對于約束于圓弧的直線擬合，引入系數約束條件不是最佳方法。Francisco等[14]以航向角為測量對象，擬合結果是航向角最優而非測點到擬合直線的垂直距離平方和最小。

假設圓弧的圓心坐標為(，)，圓的半徑為，那么圓的參數方程為：

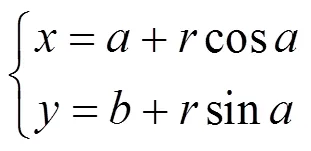
若擬合直線與圓弧的切點為(00)，圓心到點的方向角為，則

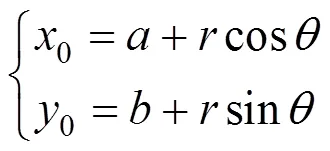
過這一點的切線方程便可以寫為：

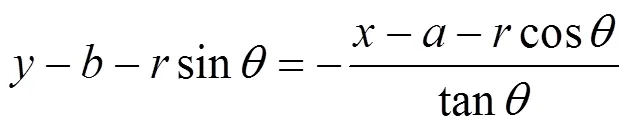
經過整理，可得：

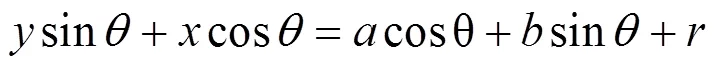
式(7)為擬合直線的回歸方程，方向角為擬合直線回歸參數。

于是第個樣本點到直線的距離的平方為：

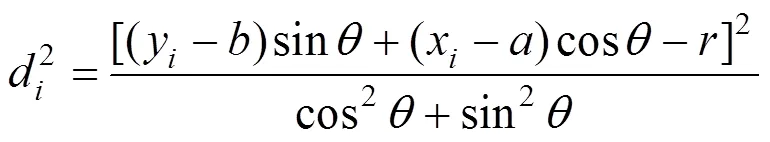
全部樣本點的距離的平方和為：

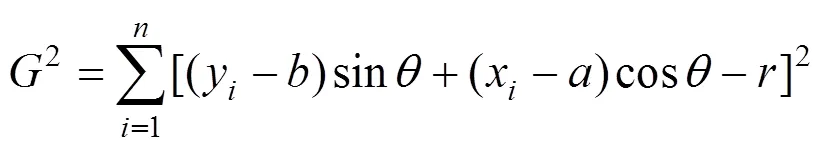
式(9)中：除了切點方向角，其他所有量都是已知量，即2是的一元單值函數。

設函數()=2，則：

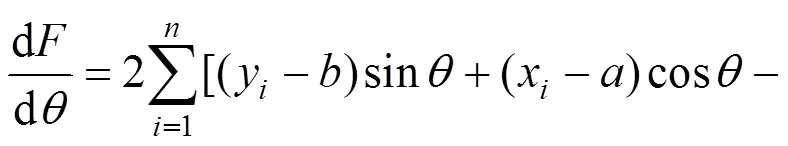
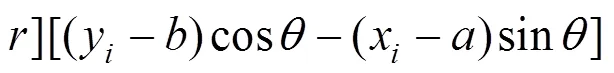
根據整體最小二乘準則，切點方向角應使()取得最小值，即()的一階導數=0。

設定

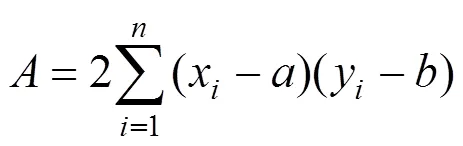
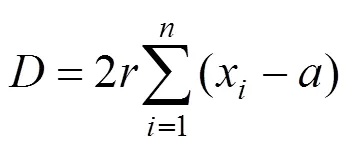
于是：

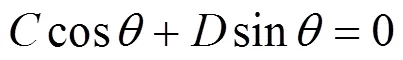
用倍角公式將其展開，可以得到下式：

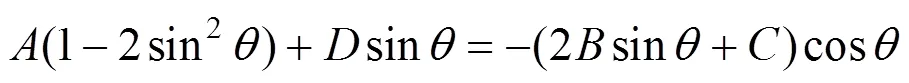
等號兩側同時平方并整理為sin的表達式：

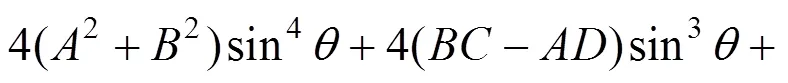
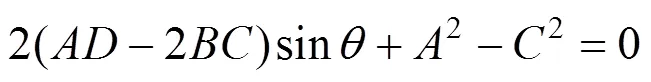
式(13)換元變形：

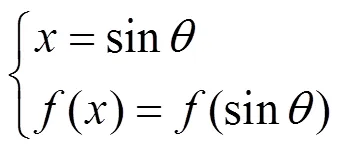
令=4(2+2)，=4()，=2+2，24，=22，則：

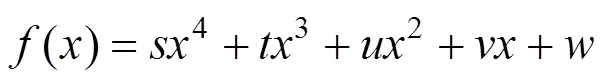
3 反拉格朗日插值迭代

方程()=0一般是一個4次方程(≠0)，其求根公式極為復雜[12]，有時會因計算機的計算誤差而導致求根結果不能滿足精度要求，有時會出現虛根。

李惠[13]在給定的區間內采用二分或切線迭代法來計算一元四次方程的近似解。每次人工給定一個區間時，如果區間內有奇數個根，則迭代出其中一個根，當區間內有偶數個根時，則給定區間內被判定為無根(因為區間兩端點的函數值乘積大于0)。因此該算法需要不斷調整初始區間，效率很低，且不穩健。

可見，迭代法求根的關鍵是計算回歸方程的單調的隔根區間。

求函數零點的迭代方法有很多種，比如牛頓迭代法、二分法等。牛頓法的收斂條件過于苛刻，不具有普遍性[15]；二分法收斂速度較慢，為此本文采用反拉格朗日插值迭代法。

如圖1，某函數在隔根區間[0，2]上存在零點，于是選擇端點(0，(0))，(2，(2))以及中點(1，(1))為初值。過這3個點可以得到一條開口向下的拋物線，這條拋物線的方程可以由拉格朗日插值公式給出。

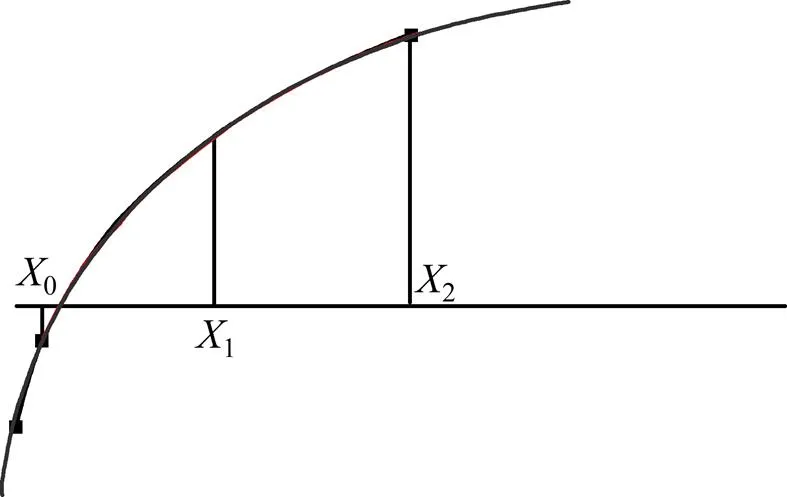
圖1 反拉格朗日插值方法

拉格朗日插值公式為：

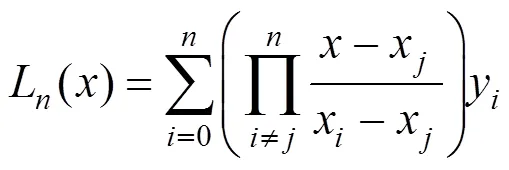
這是一個關于的次多項式。當=2，在求解2()=0時，會出現多根，增加迭代計算難度。為了讓問題盡可能的簡單化，可以把看成的因變量，構造反拉格朗日插值公式：

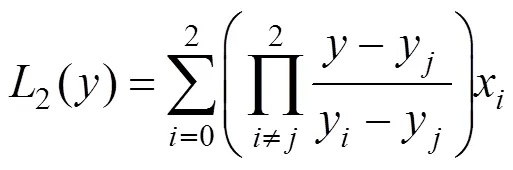
這是一條開口朝左或者朝右的拋物線，它有且只有1個根，如圖1中的曲線所示。

自此，可在[2(0),1]區間進行下一次迭代：分別以(2(0),(2(0)))和(1，(1))為端點，重復上述操作，直到lim(2(0))→0，或[2(0),1]區間距離小于閥值為止。在達到精度要求的前提下，2(0)便是方程的解。

反拉格朗日插值法并不是一種全局收斂的迭代法，只有在有單根的單調區間上才絕對收斂，證明如下：

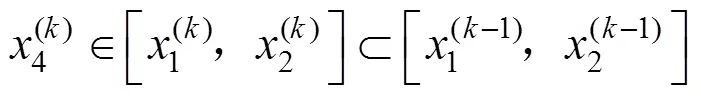
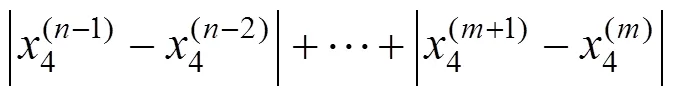
使用反拉格朗日插值法解非線性方程的具體步驟如下：

1) 初始隔根區間[0,2]，且(0)*(2)< 0；

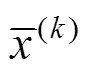
以表3和表4中的實測數據來檢驗(測點數目及坐標同表1)。

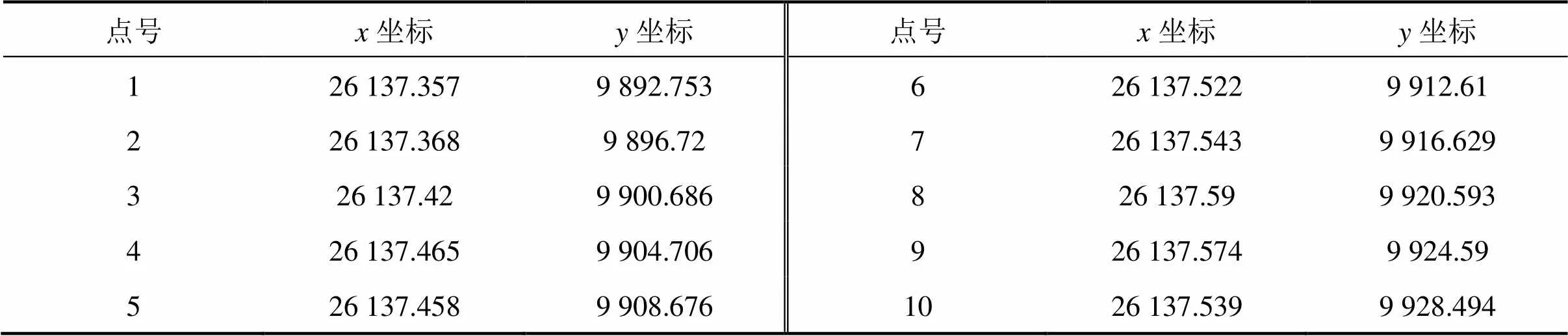
表3 10個樣本點坐標

表4 擬定圓弧坐標

計算式(15)中的參數：=1.0，=0.010 102 766 20，=?0.000 221 859 0，=?0.000 329 474 4，= ?0.000 002 278 0，精度要求為=0.000 000 001。

反拉格朗日插值法迭代8次就獲得了區間[?1，0.028 625 458 667 695 315]的近似解，二分法則需要30次迭代才能滿足精度要求，可見反拉格朗日迭代法速度快，精度高。

4 回歸參數的數值解

()=A+D?≥0，(?)=A+D+2AD≥0

可見，()和(1)都是非負值，在[?1,1]區間內，()有0~4個解，分布在4個單調區間，如圖2中的第1個曲線()。

為了求解()的單調區間，可先求出其一階導數()的所有零點。而()是一個3次函數(式(18))，仍然需要用反拉格朗日插值法來計算數值根。為此可再次求導，計算2階導函數()的零點。()是一個二次函數(式(19))，它的零點可以通過一元二次方程的求根公式直接計算。

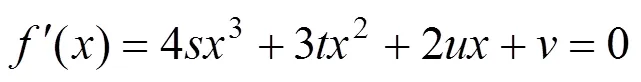
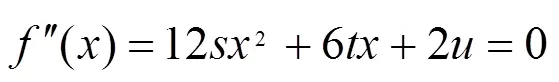
求函數()的隔根區間及數值根的計算過程如下：

1)設()0的2個解分別為21和22，如果21不存在，則令21=?1.0；如果22不存在，則令22=21；

2) 構造()函數的3個單調區間：[?1,21]，[21,22]，[22,1]，如圖2中的()曲線。

3) 單調區間內有無根的判別：求區間2個端點的函數值，如果它們的乘積為正，那么在這個區間上沒有根；如果乘積為負，那么在這個區間上有1個根。于是逐區間計算()=0的3個根31，32和33：用拉格朗日反插值法計算增區間[?1,21]內的根31(如果無根，則31=?1)，[21,22]內的根32(如果無根，則32=31)，[22,1]內的根33(如果無根，則33=32)。

4) 構造()函數的4個單調區間：[?1,31]，[31,32]，[32,33]，[33,1]。

5) 計算各單調區間的根，如果有根，則加入()=0的解集1，否則忽略該單調區間。

根據式(14)，還需要對()=0所有的解求反正弦值。設sol是從1到集合S的一個映射，并且1與S的關系為：

反正弦函數在[0, 2π]上是多值函數，一個值對應2個值。在從式(12)到式(13)的平方變形過程中，會產生增根，因此S中的元素并不一定都是方程(11)的解。為了排除增根，還應該把S所有的元素帶入方程(11)檢驗，當方程的值在誤差限范圍內時，可以被認為是方程的一個解。依次檢驗S的每一個元素，就可以得到方程(11)的解集0。

圖2 函數的隔根區間與導數0點的依賴關系

Fig. 2 Mapping between the function’s interval containing a null point and the null point of the derivative

0中的元素可以使′()=0，但并不一定能使()取到最小值。因此，還要根據式(9)求出0中每一個元素的函數值()，并比較各函數值的大小。能使得()取最小值的解才是本文問題的最優解，即與給定圓弧相切的擬合直線的回歸參數，擬合直線的斜率：

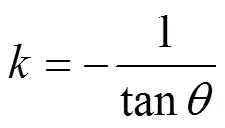
5 實例應用

為驗證本文的算法，用Microsoft Visual C++ 2008編程進行測試。這個測試中輸入數據為10個RTK測點，以及1個已經擬合的圓弧(見第3節 表2)。

運行中間成果數據即式(11)的4個系數：=?159 329.407 064 198，=?1 572 003.362 484 304，=159 400.781 899 597，=3 155 740.414 248 4(式(15)的5個系數值見第3節的檢驗)。

有效根即回歸參數=6.276 137 776 1，擬合直線斜率=141.891 314 641 1，擬合殘差的平方和為0.008 698 153 2，稍大于總體最小二乘擬合殘差的平方和，這是因為切圓使擬合直線發生了偏轉。

6 結論

1) 理論分析及實際驗證表明，將測點少、沒有緩和曲線的短小直線擬合到與圓弧相切，會使路線平面的重構結果更接近實際工況。

2) 普通最小二乘的擬合效果與測點的平面分布相關，當擬合直線的斜率絕對值越大時，擬合殘差越大。總體最小二乘擬合與測點的平面分布無關，無論直線如何傾斜，擬合殘差都相同，因此總體最小二乘的擬合效果最佳。

3) 遵循總體最小二乘準則來建立約束于圓弧的直線擬合數學模型，經換元變化，得到一個關于(sin)的一元四次方程，方程系數均是已知量的二次函數，因此計算過程簡單，易于編程實現。

4) 根據函數一階導數的0點是函數極值點原理，可以準確構建函數的隔根區間，從而降低迭代計算工作量，算法簡明實用。

[1] Casal G, Santamarina D, Vázquez-Méndez M E. Optimization of horizontal alignment geometry in road design and reconstruction[J]. Transportation Research Part C Emerging Technologies, 2017, 74(1): 261?274

[2] 劉威, 胡光常, 麻丁一, 等. 鐵路既有線平面自動重構方法研究[J]. 高速鐵路技術, 2015, 6(6): 79?84. LIU Wei, HU Guangchang, MA Dingyi, et al. Research on existing railway plane line auto-reconstruction[J]. High Speed Railway Technology, 2015, 6(6): 79?84.

[3] 郭良浩, 劉成龍, 宋韜, 等. 鐵路既有線平面和豎面線形精確分段方法研究[J]. 鐵道工程學報, 2014, 31(7): 48?52. GUO Lianghao, LIU Chenglong, SONG Tao, et al. Research on the new method for accurate linear segmentation of plane and vertical curve type in existing railway[J]. Journal of Railway Engineering Society, 2014, 31(7): 48?52.

[4] 張航, 黃云, 龔良甫. 基于三次樣條函數擬合公路平面線形方法研究[J]. 武漢理工大學學報(交通科學與工程版), 2007, 31(5): 925?927. ZHANG Hang, HUANG Yun, GONG Liangpu. Study on fitting highway alignment based on the cubic spline function[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2007, 31(5): 925?927.

[5] 劉蘇, 王文強, 查旭東, 等. 基于法線偏差的舊路平面線形擬合精度評估方法[J]. 中國公路學報, 2007, 20(5): 36?40. LIU Su, WANG Wenqiang, ZHA Xudong, et al. Estimate method for accuracy of fitting plane linear in old highway based on normal error[J]. China Journal of Highway and Transport, 2007, 20(5): 36?40.

[6] LI Wei, PU Hao, Paul Schonfeld, et al. Mountain railway alignment optimization with bidirectional distance transform and genetic algorithm[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(8): 691? 709

[7] LI Wei, PU Hao, Paul Schonfeld, et al. Methodology for optimizing constrained 3-dimensional railway alignments in mountainous terrain[J]. Transportation Research Part C, 2016, 7(68): 549?565

[8] 李偉. 鐵路數字選線關鍵技術研究與應用[D]. 長沙: 中南大學, 2014. LI Wei. Research and application for key technologies of digitalizing railway alignment design[D]. Changsha: Central South University, 2014.

[9] Robert T, Gunner L, Sarbaz O, et al. Using naturalistic field operational test data to identify horizontal curves[J]. Journal of Transportation Engineering, 2012, 138(9): 1151?1160.

[10] 丁克良, 沈云中, 歐吉坤. 整體最小二乘法直線擬合[J]. 遼寧工程技術大學學報(自然科學版), 2010, 29(1): 44?47. DING Keliang, SHEN Yunzhong, OU Jikun. Methods of line-fitting based on total least-square[J]. Journal of Liaoning Technical University (Natural Science), 2010, 29(1): 44?47.

[11] 劉元朋, 張定華, 桂元坤, 等. 用帶約束的最小二乘擬合平面圓曲線[J]. 計算機輔助設計與圖形學學報, 2001, 10(16): 1382?1385. LIU Yuanpeng, ZHANG Dinghua, GUI Yuankun, et al. Fitting planar circles with constrained least squares[J]. Journal of Computer-Aided Design & Computer Graphics, 2001, 10(16): 1382?1385.

[12] 吳佐慧, 廖軍, 徐行忠, 等. 一元三次、四次方程根的行列式解法[J]. 湖北大學學報(自然科學版), 2014, 4(36): 381?388.WU Zuohui, LIAO Jun, XU Xingzhong, et al. A solution of the root of the cubic and quartic equationusing determinant[J]. Journal of Hubei University (Natural Science), 2014, 4(36): 381?388.

[13] 李惠. 用C程序求一元四次方程的近似解[J]. 中國科教創新導刊, 2012, 9(25): 98?100. LI Hui. Find the approximate solution of a quartic equation with one unknown in C program[J]. China Education Innovation Herald, 2012, 9(25): 98?100.

[14] Francisco J C, Ana M P, José M C, et al. Use of heading direction for recreating the horizontal alignment of an existing road[J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(4): 282?299.

[15] 喻文健. 數值分析與算法[M]. 北京: 清華大學出版社, 2012: 41?45. YU Wenjian. Numerical analysis and algorithm[M]. Beijing: Tsinghua University Press, 2012: 41?45.

A recreating algorithm of straight segment of the horizontal alignment constrained by circular arc

PENG Shuhang1, PU Hao2, 3

(1. School of Areonautics, Northwestern Polytechnical University School of Areonautics, Xi’an 710072, China; 2. School of Civil Engineering, Central South University, Changsha 410075, China; 3. National Engineering Laboratory for High Speed Railway Construction, Changsha 410075, China)

On the basis of a set of (,) points, this paper proposes a method for fitting a regression line that is tangent to the given arc. The algorithm, based on Holistic Least Square Method, firstly established mathematical model fitting a line constrained by circular arc. On the basis of analysis of the intervals on which a function’s null point exists, the Inverse Lagrange’s Interpolation Method was used to calculate all of the function’s numerical solutions on the domain of definition. Additionally, the least squares criterion decided which of the numerical solutions can satisfy the mathematical model which had been established. Numerical solutions satisfying the mathematical model were exactly regression parameters of the regression line. Theoretical derivation and practical application indicate that this is a fast and stable algorithm with accurate results. This feature allows it to reconstruct precise geometric parameters of the Horizontal Alignment.

recreating the horizontal alignment; constrained line fitting; holistic least square method; intervals containing a null point; the inverse Lagrange’s interpolation method

10.19713/j.cnki.43?1423/u.2019.04.011

U412.3

A

1672 ? 7029(2019)04 ? 0915 ? 07

2018?05?05

國家自然科學基金資助項目(51608543)；國家重點研發計劃項目(2017YFB1201102)

蒲浩(1973?)，男，四川南充人，教授，博士，從事鐵路線站數字化設計理論與方法研究；E?mail：haopu@csu.edu.cn

(編輯 涂鵬)