創(chuàng)設恰當問題情境，引領課堂高效生成

甘肅 張建文

問題是驅(qū)動課堂前進的催化劑，合理而巧妙的設置問題對教學效果的提高起著至關重要的作用.本文針對習題講解過程中不同的習題類型創(chuàng)設不同的問題作一簡要說明.

1.創(chuàng)設問題的含義：學生與老師提出的問題之間形成一種這樣的情境——具有一定概括性或點撥性的問題與學生已有的認知結(jié)構(gòu)之間產(chǎn)生矛盾沖突,雖然憑現(xiàn)有的知識和技能解決起來比較困難,但學生思考的空間比較大，這樣學生的求知欲望被激發(fā)起來.在教師的幫助點撥下，經(jīng)過分析問題、探索并提出解決問題的方法、檢驗這種方法是否有效等思維活動達到掌握知識解決問題的目的.

常見的課堂提問有以下三種類型：

1.1檢測性提問：設置問題主要檢測學生對知識的理解和掌握程度，檢測學生對于學習過的知識能否順利提取或?qū)倢W過的知識能否準確表述.這種提問類型常見于新授課或復習課.

1.2引導性提問：在學生進行探索分析問題時遇到困難，教師針對學生遇到的困難進行方向性引導性的提問，目的在于指明方向點撥思路.要注意的是這種提問點而不破，問而不答.這種提問類型經(jīng)常見于習題講解課中.

1.3過渡性提問：教師在教學中為使一個教學環(huán)節(jié)向另一個教學環(huán)節(jié)過渡自然流暢而設置的轉(zhuǎn)折性問題，通常是問而有答直擊主題或者是問而不答設置懸念引起學生注意.這種類型的問題一般數(shù)量少，應用有限.

1.4系統(tǒng)連貫：問題要按照數(shù)學知識的發(fā)生發(fā)展過程，以相應的數(shù)學思想方法為主線，組成一個循序漸進的、具有內(nèi)部聯(lián)系的問題體系，系列問題應由易到難層層遞進.

2.以例點題，就題論道：以下主要結(jié)合實例說明引導性提問的原則與方法.

2.1依圖形提問引思路

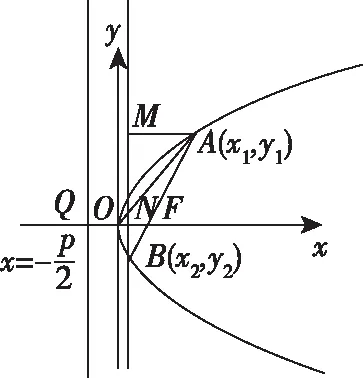
【例1】設O為坐標原點,過拋物線y2=2px(p>0)焦點F的直線l交拋物線于A,B兩點,且|AF|=3|BF|=3,則△OAB的面積為

( )

問題1.要求△OAB的面積，該如何選擇面積公式？

問題2.如何利用現(xiàn)有的條件求面積？

問題3.能否分割合并求面積？

問題4.圖中有弦有焦半徑,能否恰當利用此條件(拋物線的定義)？

過點B作y軸的平行線，交x軸于點N，過點A作AM⊥BN于點M，拋物線的準線交x軸于點Q.

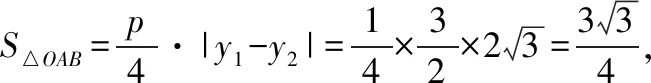
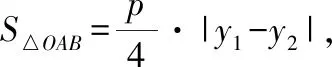
2.2依題型提問點方法

( )

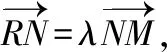
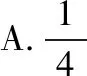
C.1 D.2

問題1.此選擇題從正面直接求解思路通暢嗎？

問題2.作圖分析有哪些量的不確定(任意的)導致其他量的不確定？

問題3.觀察選項，選項當中是確定值還是不確定的值？

問題4.選擇題的常用解答方法有哪些？

問題5.能否選用特殊化方法？

問題6.該對哪些量或元素特殊化？

問題7.該如何特殊化？

解析：用特殊化方法解答.

令p=2,則拋物線x2=4y,其焦點為F(0,1)，令過焦點F的直線l的方程為y=1，

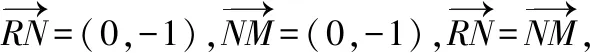
反思：此題從正面直接解答十分繁瑣，計算量比較大，而用特殊化方法解答則比較容易.提問的關鍵在于：首先正確引導學生分析題目中條件，再結(jié)合選項的特點想到用特殊化方法；

其次要將拋物線方程具體化，將直線l的位置特殊化；最后還要注意特殊化的目的是為了盡可能的簡化計算過程.

2.3依條件提問知深淺

【例3】已知函數(shù)f(x)=e2x-a2x-aex,其中e為自然對數(shù)的底數(shù),設函數(shù)f(x)的導函數(shù)為f′(x).

(Ⅰ)試討論函數(shù)f′(x)的單調(diào)性;

(Ⅱ)當a>0時，若2e2x-aex≥a2-2a恒成立,求實數(shù)a的取值范圍.

引導解答(Ⅰ):

問題1.題目求解的是哪個函數(shù)的單調(diào)性？

問題2.要求其單調(diào)性，只需要判定哪個函數(shù)的正負？

問題3.判定正負是否涉及參數(shù)討論？

問題4.參數(shù)討論的標準是什么？

解析：因為f(x)=e2x-a2x-aex,x∈R,故f′(x)=2e2x-aex-a2,x∈R.

下面判定f′(x)的單調(diào)性,令f′(x)=g(x)，則g′(x)=4e2x-aex=ex(4ex-a),x∈R.

(1)當a≤0時，g′(x)>0恒成立,故f′(x)在R上單調(diào)遞增;

(2)當a>0時，令g′(x)>0,可得x>lna-2ln2；令g′(x)<0 ,可得x

所以函數(shù)f′(x)在(lna-2ln2,+∞)上單調(diào)遞增,在(-∞,lna-2ln2)上單調(diào)遞減.

反思：此題是一道高三模擬題，雖然難度不大，但是答題的效果確實不太好，主要原因是絕大多數(shù)學生想當然的去求解函數(shù)f(x)的單調(diào)性，而題目要求解的是函數(shù)f′(x)的單調(diào)性.教師引導學生解答此題首先要明確題目要求，其次要對參數(shù)準確討論，最后要注意模塊化思想及轉(zhuǎn)化化歸思想.

2.4依結(jié)構(gòu)提問減運算

下面對例3中(Ⅱ)進行引導解答：

問題1.解答恒成立問題的常用方法有哪幾種？

問題2.此題用整體法解答能否進行？

問題3.能否應用(Ⅰ)的結(jié)論？

問題4.如何將式子結(jié)構(gòu)轉(zhuǎn)化成(Ⅰ)中的f′(x)？

解析：當a>0時，2e2x-aex≥a2-2a恒成立, 則2e2x-aex-a2≥-2a恒成立.

由(Ⅰ)可知, 當a>0時,f′(x)=2e2x-aex-a2,函數(shù)f′(x)在(lna-2ln2,+∞)上單調(diào)遞增,在(-∞,lna-2ln2)上單調(diào)遞減.

所以f′(x)≥-2a在x∈R上恒成立，只需滿足f′(x)min≥-2a即可.

反思：簡化計算過程，提高運算速度與質(zhì)量，關鍵在于巧妙利用現(xiàn)有的結(jié)論與條件，縱觀全局，抓主抓重才可以因勢利導，借力打力，達到四兩撥千斤的效果.就本題而言,要明確(Ⅰ)的解答是對原題目條件的進一步深度加工，在之后的計算求解中是可以繼續(xù)應用的；另外還得將(Ⅱ)中的式子結(jié)構(gòu)向(Ⅰ)靠攏.

2.5依要求提問明是非

【例4】《九章算術(shù)》是我國的古代數(shù)學名著,它在幾何學中的研究比西方早一千多年,其中有很多對幾何體體積的研究.已知A,B,C均在球O的表面上,且∠AOB=90°,若三棱錐O-ABC的體積V的最大值為36,則當V最大時三棱錐O-ABC的外接球體積為

( )

C.144π D.108π

問題1.作圖畫球O,三棱錐O-ABC的體積V何時最大？

問題2.三棱錐O-ABC的體積V最大時，三條棱OA,OB,OC之間有什么關系？

問題3.三棱錐O-ABC的外接球是不是球O？

問題4.求解三棱錐的外接球半徑的常用方法是什么？

解析：通過作圖可知：

三棱錐O-ABC的體積V最大時,OA,OB,OC兩兩垂直，設球O的半徑為R,

則有OA=OB=OC=R,且OA⊥OB,OA⊥OC,OC⊥OB,

設三棱錐O-ABC的外接球半徑為r,體積為V′,

反思：在本題的解答過程中,學生很容易錯誤的將三棱錐O-ABC的外接球理解為球O,因此要順利引導學生理解球O并不是三棱錐O-ABC的外接球.

2.6依臨界提問現(xiàn)思想

【例5】已知圓C:(x-1)2+(y-4)2=10和點M(5,t),若圓C上存在兩點A,B使得MA⊥MB,則實數(shù)t的取值范圍是

( )

A.[-2,6] B.[-3,5]

C.[2,6] D.[3,5]

問題1.點M與圓C的位置關系是什么？點M是否在圓外？

問題2.已知A,B為圓C上兩點,當AM,BM為圓C切線時,∠AMB有何特點(最大還是最小)？

問題3.當AM,BM為圓C切線時,點M與圓越近時,∠AMB變大還是變小？

問題4.當AM,BM為圓C切線時,|CM|為何值(臨界值)時∠AMB=90°？

問題5.當AM,BM為圓C切線,|CM|減小時,∠AMB是變大還是變小？

問題6.要存在A,B使得∠AMB=90°,|CM|要大于臨界值還是小于臨界值？

已知A,B為圓C上兩點,當AM,BM為圓C切線時,∠AMB最大,

解得t∈[2,6]，故選C.

反思：本題的解答關鍵在于引導學生體會數(shù)形結(jié)合思想和運動變化思想.入手點在于臨界條件的分析,重點在于理解透徹三條：第一,當AM,BM為圓C切線時,∠AMB最大;第二, |CM|減小時,∠AMB增大;第三,要滿足存在性條件,|CM|就要小于等于臨界值.

3.總結(jié)與展望