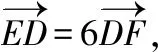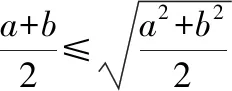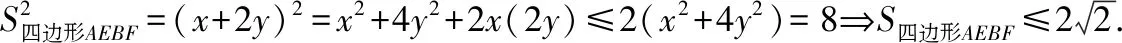高考不等式專題解決問題的思考與對策
福建 周白生
眾所周知,不等式是高中數(shù)學(xué)的重點(diǎn)和難點(diǎn),一直以來都是高考熱點(diǎn)內(nèi)容.從近幾年的高考試題來看,對不等式重點(diǎn)考查的有四種題型:解不等式、證明不等式、不等式的應(yīng)用、不等式的綜合性問題.考查的內(nèi)容及其難度主要有以下幾點(diǎn):(1)不等式的性質(zhì),基本不等式和絕對值不等式的考查,大多出現(xiàn)在選擇題或填空題中,一般屬于容易題或中檔題.因此,關(guān)于這一部分的知識(shí),重在記憶并理解基本公式. (2)含參的不等式問題是近幾年較多的一種題型,特別是不等式恒成立問題中參數(shù)取值范圍的求法.(3)不等式幾乎能與所有數(shù)學(xué)知識(shí)建立廣泛的聯(lián)系,通常以不等式與函數(shù)、三角、向量、解析幾何、數(shù)列的綜合問題的形式出現(xiàn),綜合考查學(xué)生的數(shù)學(xué)抽象、邏輯推理及數(shù)學(xué)運(yùn)算等核心素養(yǎng),問題多屬于中檔題甚至是難題,對不等式的知識(shí)、方法與技巧要求較高.在現(xiàn)行各版本高中教材中,除選修4—5“不等式選講”外,只在必修5第三章“不等式”與選修1—2(文)、選修2—2(理)第二章“推理與證明”中涉及不等式相關(guān)內(nèi)容,所以不等式課時(shí)安排應(yīng)該算是比較少的.下面根據(jù)近年高考不等式專題答題情況對學(xué)生存在的主要問題進(jìn)行剖析.
1.關(guān)注平面區(qū)域作圖教學(xué)
高考試卷中線性規(guī)劃是每年必考的問題,從近幾年試題情況看線性規(guī)劃問題主要考查不含參數(shù)截距式問題,不等式組含參數(shù)、目標(biāo)函數(shù)不含參數(shù)問題,不等式組不含參數(shù)、目標(biāo)函數(shù)含參數(shù)問題,基本出現(xiàn)的形式都是線性形式,所以平面區(qū)域的確定是解題的關(guān)鍵,要確定平面區(qū)域的關(guān)鍵在于根據(jù)直線方程作出對應(yīng)直線.
本問題學(xué)生答題情況不理想主要原因大致有兩點(diǎn),第一點(diǎn):沒有按統(tǒng)一標(biāo)準(zhǔn)確定可行域.第二點(diǎn):不能正確理解目標(biāo)函數(shù)所表示的幾何意義,也就是不能順利將這個(gè)代數(shù)式轉(zhuǎn)化為幾何問題進(jìn)行求解.解答本問題的根本就是依據(jù)統(tǒng)一標(biāo)準(zhǔn)(以點(diǎn)定域或是以x的系數(shù)或者以y的系數(shù)作為統(tǒng)一標(biāo)準(zhǔn))確定區(qū)域,然后通過數(shù)形結(jié)合的方法確定最優(yōu)解.


2.強(qiáng)化“分類討論”意識(shí)
分類討論就是當(dāng)對所給問題無法一次研究到位時(shí),要對問題分類進(jìn)行研究并得出每類結(jié)論,最后綜合各類結(jié)果得到整個(gè)問題的答案.分類時(shí)學(xué)生存在遺漏或重復(fù)、分層次、越級討論等錯(cuò)誤.導(dǎo)數(shù)是高中研究函數(shù)性質(zhì)的重要工具,甚至筆者曾經(jīng)在學(xué)校里聽課時(shí),就聽到老師講到函數(shù)與導(dǎo)數(shù)這個(gè)模塊,表示問題解決的辦法就是求導(dǎo),也就是拿到題目不管“三七二十一”,求導(dǎo)后再說.不可否認(rèn)學(xué)生經(jīng)歷模式化的求導(dǎo)訓(xùn)練后,對于求導(dǎo)運(yùn)算基本沒有問題,那么現(xiàn)在問題就變?yōu)椤髮?dǎo)后要干嘛?求導(dǎo)后對應(yīng)關(guān)系已經(jīng)變化,此時(shí)應(yīng)對導(dǎo)函數(shù)進(jìn)行研究,觀察導(dǎo)函數(shù)結(jié)構(gòu)是“一次函數(shù)”“二次函數(shù)”或者是“超越函數(shù)”.如果導(dǎo)函數(shù)是“一次函數(shù)”學(xué)生還算駕輕就熟,如果是“二次函數(shù)”或者是“超越函數(shù)”時(shí),學(xué)生往往表現(xiàn)得手足無措,我想這也是導(dǎo)數(shù)綜合應(yīng)用問題經(jīng)常讓學(xué)生害怕的原因.
函數(shù)求導(dǎo)后若要分類討論,此時(shí)函數(shù)類型一般是一次函數(shù)型或者和一二次函相關(guān)的分式函數(shù),教學(xué)中應(yīng)著重強(qiáng)調(diào)怎么抓住分類討論臨界點(diǎn).特別是對于函數(shù)與導(dǎo)數(shù)中的參數(shù)分類,那么這時(shí)候分類討論的依據(jù)一般是從方程的根入手.而求方程的根最直接的方法就是因式分解,也就是能分解盡量先分解,不能分解時(shí),若為二次函數(shù)那么應(yīng)求出其判別式,若為超越式那么應(yīng)該繼續(xù)求導(dǎo),也就是導(dǎo)后求導(dǎo)題型.

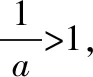


②當(dāng)a=1時(shí),恒有f′(x)≤0,
∴f(x)的單調(diào)遞減區(qū)間為(0,+∞).
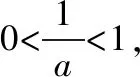

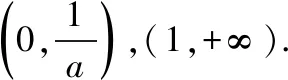

當(dāng)a=1時(shí),f(x)的單調(diào)遞減區(qū)間為(0,+∞);
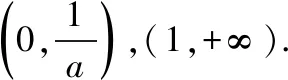
3.規(guī)范簡單的不等式證明書寫條理性
不等式選考中證明的常見方法,有分析法、綜合法、反證法、換元法等,難度不大,學(xué)生主要是解題規(guī)范性較差,失誤和失分最多的是會(huì)而不對、對而不全和全而不準(zhǔn),書寫混亂,解答過程缺失關(guān)鍵步驟,丟三落四等.
大部分題目形式上是考查不等式證明,實(shí)際主要是在考查不等式的相關(guān)性質(zhì)基礎(chǔ)上,結(jié)合考查充要條件的判斷,所以學(xué)生要拿到關(guān)鍵分還應(yīng)多加注意不等式證明書寫的條理性.教師在培養(yǎng)學(xué)生邏輯推理能力的同時(shí)也有必要向?qū)W生展示正確的書寫格式,這正與近些年提出的一節(jié)課應(yīng)有一個(gè)知識(shí)點(diǎn)完整的板書過程相呼應(yīng),同時(shí)也說明了書寫條理性的重要.
【例3】(2015·全國卷Ⅱ理·24)選修4 - 5:不等式選講
設(shè)a,b,c,d均為正數(shù),且a+b=c+d,證明:
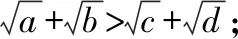
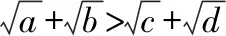


(Ⅱ)(i)若|a-b|<|c-d|,則(a-b)2<(c-d)2,即(a+b)2-4ab<(c+d)2-4cd,

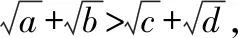
∵a+b=c+d,∴ab>cd,于是(a-b)2=(a+b)2-4ab<(c+d)2-4cd=(c-d)2,
因此|a-b|<|c-d|.
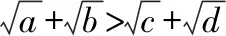
4.加強(qiáng)學(xué)生讀題析題的能力
從近幾年高考命題特點(diǎn)上看,綜合應(yīng)用意識(shí)以及在現(xiàn)實(shí)生活中的實(shí)際應(yīng)用已經(jīng)成為命題專家著重考查的部分,復(fù)習(xí)中,應(yīng)規(guī)范教學(xué)的閱讀指導(dǎo).應(yīng)該呈現(xiàn)讀題提取關(guān)鍵信息、析題形成解題思路、解題示范規(guī)范表達(dá)、反思積淀解題經(jīng)驗(yàn)的“四步曲”完整過程,才能充分發(fā)揮解題教學(xué)的效益.其次,加強(qiáng)平時(shí)的閱讀訓(xùn)練.需要適當(dāng)增加平時(shí)作業(yè)習(xí)題的閱讀量,尤其是與實(shí)際應(yīng)用性相結(jié)合的試題的讀題訓(xùn)練,充分提高學(xué)生的閱讀理解能力.
線性規(guī)劃結(jié)合實(shí)際問題往往需要學(xué)生具備良好的數(shù)形結(jié)合及數(shù)學(xué)建模能力,通過題目所給信息明確解題目標(biāo),也就是將實(shí)際問題數(shù)學(xué)化的過程,即將“文字語言”表達(dá)的條件和目標(biāo)轉(zhuǎn)化為數(shù)學(xué)的“符號(hào)語言”進(jìn)而解決問題.本類題型一個(gè)很大的特點(diǎn)就是信息量大,這有別于傳統(tǒng)的短小精悍的數(shù)學(xué)題,會(huì)讓學(xué)生產(chǎn)生不適感,所以教師在教學(xué)上應(yīng)特別注重學(xué)生讀題析題能力的培養(yǎng).
【例4】電視臺(tái)播放甲、乙兩套連續(xù)劇,每次播放連續(xù)劇時(shí),需要播放廣告.已知每次播放甲、乙兩套連續(xù)劇時(shí),連續(xù)劇播放時(shí)長、廣告播放時(shí)長、收視人次如下表所示:

連續(xù)劇播放時(shí)長(分鐘)廣告播放時(shí)長(分鐘)收視人次(萬)甲70560乙60525
已知電視臺(tái)每周安排的甲、乙連續(xù)劇的總播放時(shí)間不多于600分鐘,廣告的總播放時(shí)間不少于30分鐘,且甲連續(xù)劇播放的次數(shù)不多于乙連續(xù)劇播放次數(shù)的2倍.分別用x,y表示每周計(jì)劃播出的甲、乙兩套連續(xù)劇的次數(shù).
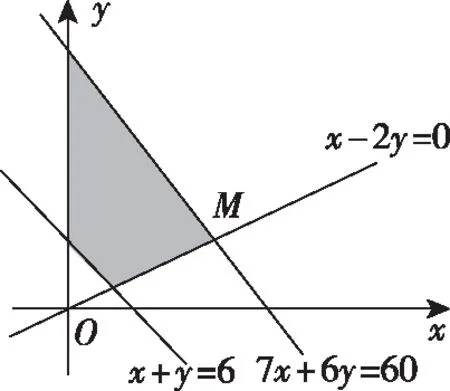
(Ⅰ)用x,y列出滿足題目條件的數(shù)學(xué)關(guān)系式,并畫出相應(yīng)的平面區(qū)域;
(Ⅱ)問電視臺(tái)每周播出甲、乙兩套連續(xù)劇各多少次,才能使總收視人次最多?
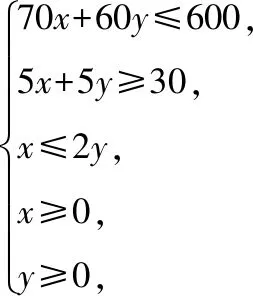
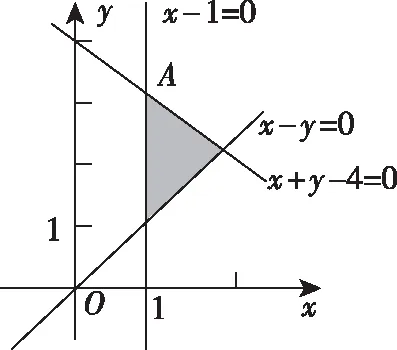
平面區(qū)域如圖中陰影部分所示.
(Ⅱ)設(shè)總收視人次為z萬,則目標(biāo)函數(shù)為z=60x+25y.

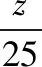
又∵x,y滿足約束條件,
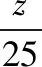
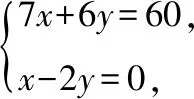
∴電視臺(tái)每周播出甲連續(xù)劇6次、乙連續(xù)劇3次時(shí)才能使總收視人次最多.
5.重視基本性質(zhì)特征的教學(xué)
高考數(shù)學(xué)試題在不等式內(nèi)容方面考查的主要問題是其基本性質(zhì)特征,但是由于不等式的難度較大、技巧較多,所以多以不等式基本性質(zhì)特征為主要考查內(nèi)容.命題者常常希望借助不等式強(qiáng)大的融合功能,將其與其他主干知識(shí)交匯在一起進(jìn)行命題,綜合考查學(xué)生邏輯推理等數(shù)學(xué)核心素養(yǎng),這就要求學(xué)生具有較強(qiáng)的綜合模塊知識(shí)的能力,能夠在考查以其他主干知識(shí)為載體的試題背景下,靈活地應(yīng)用不等式相關(guān)性質(zhì)進(jìn)行求解.學(xué)生這方面的能力是比較欠缺的.所以教師在不等式性質(zhì)教學(xué)上應(yīng)重視基本性質(zhì)特征,應(yīng)盡可能向?qū)W生還原數(shù)學(xué)知識(shí)的本質(zhì),在面對知識(shí)內(nèi)容較多,解決角度較多的情況下尤其應(yīng)注意萬變不離其宗,應(yīng)保持以不變應(yīng)萬變的積極心態(tài).例如所給條件既有對數(shù)式又有指數(shù)式時(shí),解決問題的基本思路應(yīng)是“化統(tǒng)一”“抓根本”,“化統(tǒng)一”指的是將式子的形式變?yōu)榻y(tǒng)一,“抓根本”就是雖然不等式的很多性質(zhì)在我們解決數(shù)的大小比較上可能幫助很大,但是真正比較大小的主線還是函數(shù)的單調(diào)性,這才是真正的數(shù)學(xué)本質(zhì).
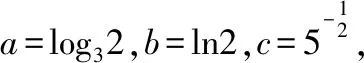
( )
A.a C.c 命題者思考的另一個(gè)問題是如何能夠找到一種數(shù)學(xué)工具,將某些難以聯(lián)結(jié)起來的相關(guān)知識(shí)進(jìn)行融合,同時(shí)能夠命制出生動(dòng)而又有一定難度的試題來,不等式當(dāng)然是其中之一!在數(shù)學(xué)教學(xué)過程中,我們有時(shí)會(huì)發(fā)現(xiàn),有些知識(shí)的聯(lián)結(jié)存在不對等的關(guān)系,但是難以用代數(shù)等量之間的關(guān)系來表達(dá),這時(shí)如何將這些相關(guān)知識(shí)進(jìn)行融合就顯得很重要了,而不等式正是能夠體現(xiàn)這一考查方式的內(nèi)容之一.近些年不等式強(qiáng)大的融合功能表現(xiàn)得越來越明顯了,基本上試卷的壓軸題里都有它的“身影”存在.因此在教師的“教”和學(xué)生的“學(xué)”上要時(shí)刻想到不等式的工具作用,尤其在求解最值問題或范圍問題上. 【例6】設(shè)橢圓中心在坐標(biāo)原點(diǎn),A(2,0),B(0,1)是橢圓兩個(gè)頂點(diǎn),直線y=kx(k>0)與AB相交于點(diǎn)D,與橢圓相交于E,F(xiàn)兩點(diǎn). (Ⅰ)求橢圓的標(biāo)準(zhǔn)方程; (Ⅲ)求四邊形AEBF面積的最大值. 解法2:由上述解法1并結(jié)合基本不等式2ab≤a2+b2可得,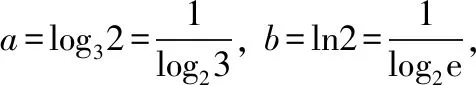
6.強(qiáng)化不等式工具的認(rèn)識(shí)