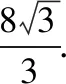平面向量問題的幾種處理策略

安徽 蔣玉芳 張道梅

在以往高考中，從平面向量的命題形式可以看出，整個命題過程緊扣課本，重點突出，有時考查單一知識點，有時通過知識的交匯與鏈接，全面考查平面向量的有關概念、線性運算、數量積及坐標運算等內容．試題難度多為容易題或中檔題，少數為選擇或填空的壓軸題，尤其是近幾年的高考和模擬考試中，平面向量難度有所提升，難點多為求解數量積的取值范圍、模的取值范圍等問題，與其關聯的知識點有函數、直線與圓、基本不等式等，題目綜合性比較強，大多數學生求解起來相對困難.那么對于這類問題有什么好的處理策略嗎？下面本文將呈現出針對該難點的幾種處理策略.

【策略一】基底法

此法所涉及的知識點是平面向量的線性運算及平面向量基本定理，即將題目涉及的所有向量，通過線性運算統一成兩個不共線的向量，即“多元”變“少元”.這樣處理的好處是使題干的條件所表達的含義更“透明”，思路更清晰，性質運用得更合理.具體的解題步驟是：①通過題干合理選取基底；②利用線性運算，統一向量；③結合已知建立等量關系或函數關系等即可求解.

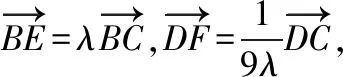
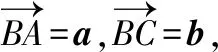
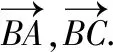
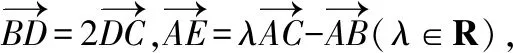
【策略二】構造平面直角坐標系

平面向量是連接代數與幾何的橋梁，尤其是平面向量的坐標運算的引入，使得向量與代數的互換運算更是深入人心.一些基于考查向量和代數的互換運算的好題應運而生，這些題目絕大多數都有一個很顯著的特征：已知某兩個向量所成角.通過這個已知即可建立平面直角坐標系進行求解.具體解題步驟是：①通過題干，合理建系；②將所有向量轉化為坐標形式；③利用向量的坐標運算公式和法則對原題進行轉化與化歸；④在最后的計算時，往往需要借助函數、基本不等式、平面幾何等知識方可求解.

( )

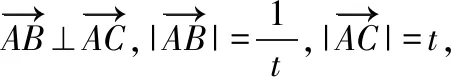
A.13 B.15

C.19 D.21

【解析】以A為坐標原點，建立平面直角坐標系，如圖所示，

( )

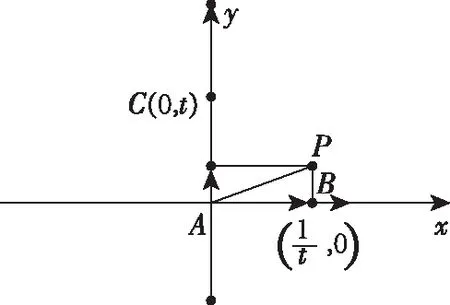
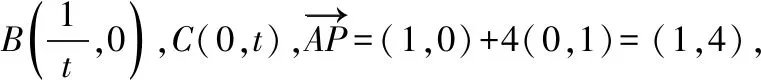
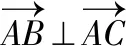
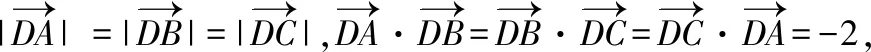
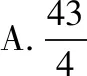
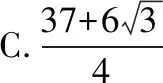
【答案】B．

【策略三】構造圖形

在策略二中，談到平面向量是連接代數與幾何的橋梁，也已經了解了向量與代數之間是如何轉換的，那么向量與幾何之間又是通過什么進行轉化的呢？一種轉化方式是通過平面向量的幾何意義“構造平面圖形”，使問題圖形化，此種轉化稱為“形化”.而對于平面向量中有關最值問題通過“形化”后， 問題更具有直觀性，即可借助于平面圖形的特征直接進行判斷.此法具體解題步驟是：①將題干向量用有向線段表示；②通過已知構造圖形；③判斷動點軌跡；④利用動點軌跡的特征即可求解.

( )

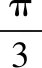
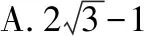
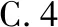
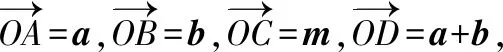
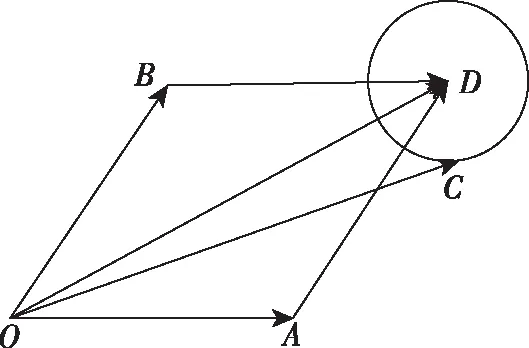
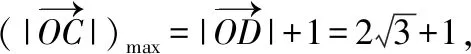
【評注】通過此題可以發現，利用平面圖形解決向量問題更清晰、更簡潔.而此法需要學生對平面向量的幾何意義和一些特殊的平面圖形特征的熟練掌握，同時對學生空間想象能力也有一定的要求.

【變式3】(2017·浙江寧波2模)已知|a|=|b|=1，a與b夾角為90°，若c滿足(a-c)(b-c)=0，則|c|的最大值是________．

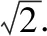
【策略四】極化恒等式

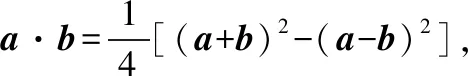
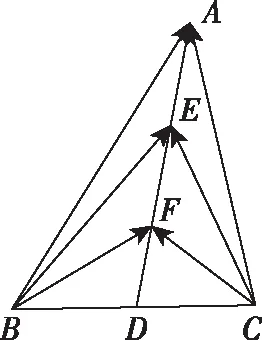
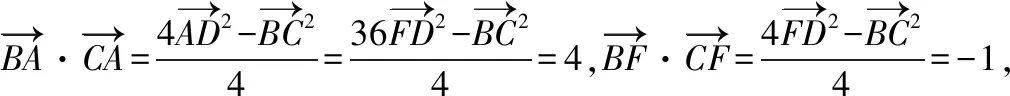
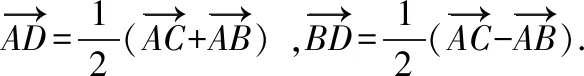
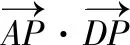
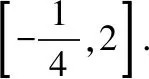
【策略五】利用等和線

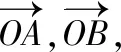
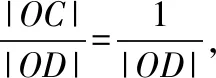
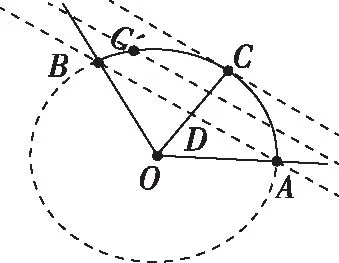
【評注】此法和“極化恒等式”有異曲同工之處，都源于教材，又高于教材，其本質是平面向量共線基本定理的推論和數乘向量.同時此法也考查了數形結合思想.

( )

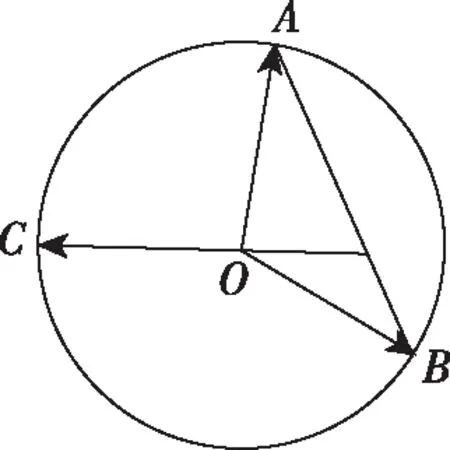
A.1 B.2

【答案】C.

【答案】[-2,-1).

【策略六】利用平面向量數量積的幾何意義

利用平面向量數量積的幾何意義求解平面向量數量積問題，具有直觀性和簡捷性的特點,同時它具有的靈活性也使得它不易被掌握,但用好向量的數量積的幾何意義能使和數量積有關求值、求最值、求范圍等問題的解決變得更加簡單.

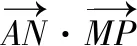
【解析】過M點作AN的垂線，垂足為D，如圖所示,

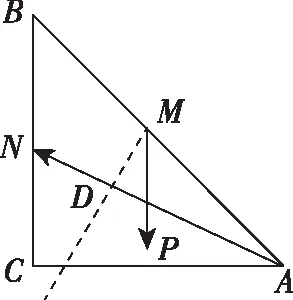
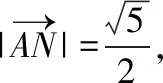
【評注】此題如果不用向量數量積的幾何意義同樣也可得到正解，但可能稍顯麻煩,用幾何意義來解則更加簡潔、更加直觀，在計算方面只需著力計算長度和夾角的余弦值,但要注意先判斷所求向量的夾角的情況，若夾角為鈍角,則數量積為負；若夾角為銳角,則數量積為正；若夾角為直角,則數量積為零.

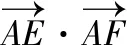
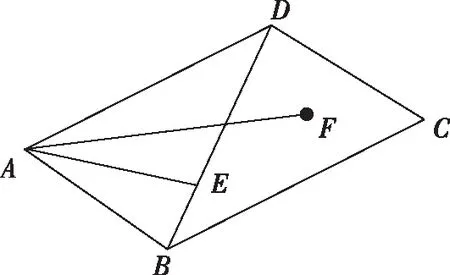
【答案】[9,18].

【策略七】換元法

換元法在函數、多元變量最值、平面解析幾何初步中的應用耳熟能詳，但在平面向量中，卻不能被熟知，而換元法更能有效地將平面向量、代數、幾何有機結合，完美地體現了向量這個重要的解題工具.在向量中換元法主要體現在兩種換元思想：①構造新向量思想進行換元；②利用代數思想進行換元.在此筆者重點談“利用代數思想進行換元”，此思想主要解決和向量模有關的問題.具體應用如下：

【例7】(2017·浙江卷·15)已知向量a,b滿足|a|=1,|b|=2,則|a+b|+|a-b|的最小值是________，最大值是________．

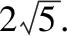
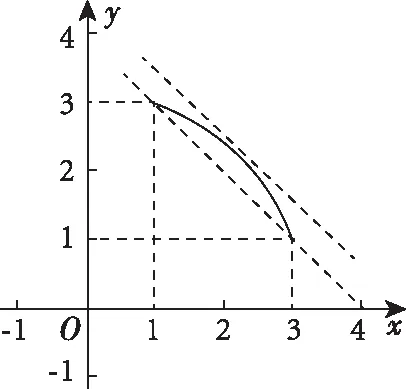
【評注】此法先對|a+b|,|a-b|進行換元，再對|a+b|=x，|a-b|=y兩邊平方，最終轉化為直線z=x+y與曲線x2+y2=10(x,y∈[1,3])的位置關系，完美地詮釋了向量是連接代數和幾何的橋梁.但利用此法，有一個易錯點，是換元變量的范圍問題，如本題中的x,y的范圍.

【變式8】(2018·浙江麗水一模)已知|m|=2,|m+2n|=2,則|2m+n|+|n|的最大值為________.