2018年全國卷Ⅰ理科解析幾何第19題的解析和探究

廣東 鄭燦基

1.試題

2018年高考全國卷Ⅰ理科第19題試題如下：

(1)當l與x軸垂直時，求直線AM的方程；

(2)設O為坐標原點，證明：∠OMA=∠OMB.

本題立意新穎，內涵豐富，考查了直線的方程、斜率、直線與橢圓的位置關系、韋達定理、兩角相等的等價轉化處理，是一道綜合性較強的試題.試題分為兩問，層次明顯，第一問注重基礎，難度較小；第二問有一定的難度，重點檢測學生的運算求解能力、推理論證能力等，突出對數學核心素養的考查.以下著重討論第二問的解法.

2.解法呈現

【思路1】證明兩直線的斜率之和為零.

證法1：當l與x軸重合時，∠OMA=∠OMB=0°.

當l與x軸垂直時，OM為AB的垂直平分線，所以∠OMA=∠OMB.

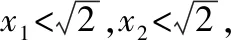
綜上，∠OMA=∠OMB.

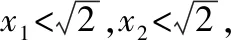
【思路2】利用對稱性，證明三點共線.

【思路3】到角兩邊距離相等的點在角平分線上.

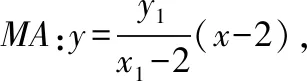
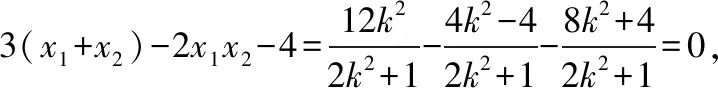
【思路4】利用角平分線定理和直線的參數方程

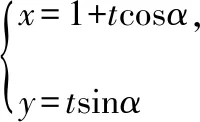
設A(1+t1cosα,t1sinα)，B(1+t2cosα,t2sinα),M(2,0)，

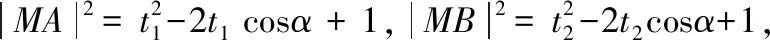
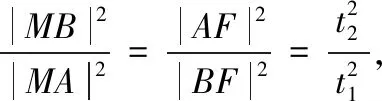
【思路5】利用相似三角形進行轉化.

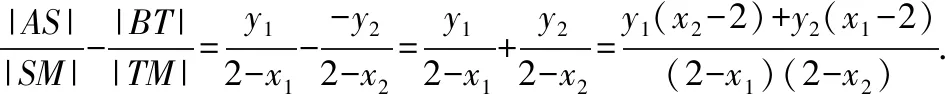
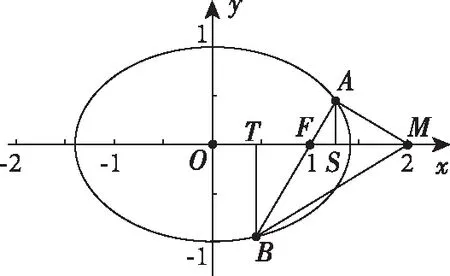
【思路6】利用橢圓的第二定義和平面幾何知識解決

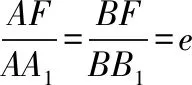
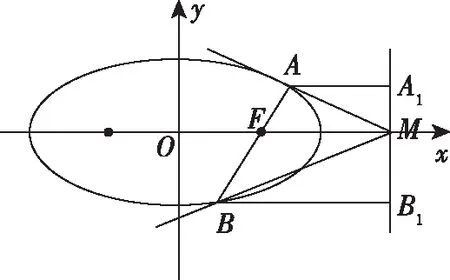
需要指出的是，思路1的兩種證法都是將幾何問題轉化為代數運算，不同的是直線方程的假設形式.證法1是常規算法，即用點斜式法設直線方程為y=k(x-1)，帶來的結果是在①中多處出現參數k和k2，運算較為繁瑣，且不完備(不包含斜率不存在的情形).而證法2是把直線設為x=my+1，把x看作y的函數，求解過程較為簡單，得到的②式中含m的頻數少，而且完備性好，包括了滿足所有條件的直線方程.同時，在接下來的運算中較為簡潔.因此，根據題設條件特點，選用恰當的直線和圓錐曲線方程是強化求簡、降低計算的重要手段.一般而言，若直線過的點是(0,t),我們常把直線假設為y=kx+t(假設斜率存在)，而若直線過的點是(t,0),我們常假設直線的方程為x=my+t，這樣可以高效解題.

3.引申探究

3.1顯性結論

本題中第二問實質上揭示了橢圓的一個性質：橢圓C的準線與長軸的交點M和過相應的焦點F的弦的兩端點A,B連線所成角∠AMB被長軸平分.在雙曲線、拋物線中也有類似的性質：

①雙曲線C的準線與實軸的交點M和過相應的焦點F的弦的兩端點A,B連線所成角∠AMB被實軸平分.

②拋物線C的準線與對稱軸的交點M和過相應的焦點F的弦的兩端點A,B連線所成角∠AMB被對稱軸平分.

其證明仿照上面高考題的證法，過程略.以上結論可以統一為：

定理1：圓錐曲線準線與長軸(或實軸、或對稱軸)的交點M和相應的焦點弦端點A,B連線所成的角∠AMB被長軸(或實軸、或對稱軸)平分.

3.2隱性結論

上面結論中AB是圓錐曲線過焦點的弦,M點是圓錐曲線準線與對稱軸的交點，如果AB是圓錐曲線中任意一條弦，點M是與對稱軸垂直的直線與該對稱軸的交點，那么圓錐曲線是否也有類似的性質呢？

利用《幾何畫板》實驗，筆者發現如下性質：

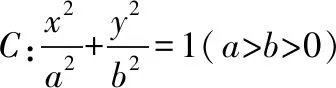
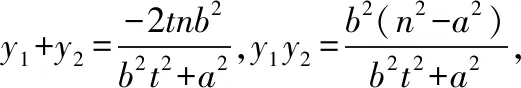
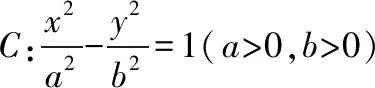
③已知拋物線C:y2=2px(p>0)和x軸上的兩點M,N(xN>0)，過點N引直線交拋物線C于A,B兩點，則∠AMN=∠BMN?xM=-xN.

性質②和③的證明類似性質①，故省略.

以上性質可統一為：

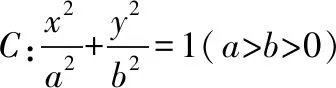
3.3進一步研究

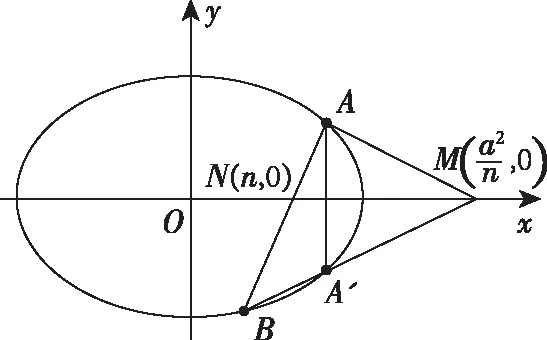
以此類推，不難得到如下結論：

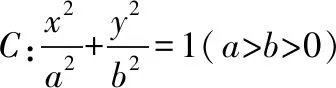
過拋物線C:y2=2px(p>0)的對稱軸上的一點N(n,0)(n>0)作弦AB，點A(或點B)關于x軸的對稱點為A′(或B′)，則點A′,B,M(-n,0)(或A,B′,M(-n,0))三點共線.

3.4條件與結論互換

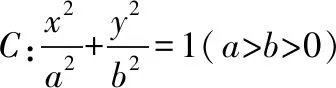
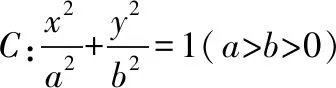
4.結束語