一道解三角形試題的探究與賞析
廣東 楊偉達
一、試題呈現
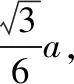
考點分析:本題以三角形為背景,以正余弦定理、三角恒等變換、最值為載體,在正余弦定理、三角函數、不等式等基礎知識的交匯處精心設計,本題考查了學生邏輯推理能力、轉化與化歸能力、運算求解能力.試題背景熟悉,條件簡單清晰,表述簡潔,對數學知識、思想方法能有效地考查,能較好地甄別學生的數學思維水平和數學潛能,是一道看似平淡無奇,實則內涵豐富的好題.
二、思路探究及解答過程
1.題目已知條件是什么?結論是什么?未知量是什么?嘗試用自己的語言表述.
本題已知條件涉及△ABC邊BC的高,題設目標求最大值,涉及熟悉的基本不等式結構.
2.思維障礙
本題看似熟悉但又陌生,不少學生看到基本不等式結構就秒殺,其結果是錯誤的,因為它不是求最小值,而是求最大值,且題目條件僅涉及三角形的高,需要挖掘三角形的隱含條件,不少學生沒見過此類題型,一時無從下手,只能望題興嘆.
3.常見相關類型題目及解題思路
有關三角形為背景的題型通常用正余弦定理、三角恒等變換處理,最終回歸到函數或三角函數形式處理最值.
解法一(正余弦定理+輔助角公式)
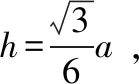



在△ABC中,a2=b2+c2-2bccosA, ④
由③④得b2+c2=4bcsin(A+30°),


點評:從三角形的面積公式出發,利用正余弦定理、三角恒等變換、輔助角公式,最后利用三角函數的有界性求解. 這種解題過程思路清晰、自然,運算簡單,方便求解.
解法二(函數法)

在△ABC中a2=b2(1+x2)-2b2xcosA, ①

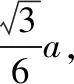
①④聯立化簡得x2-4sin(A+30°)x+1=0,
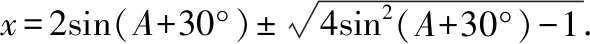
不妨令sin(A+30°)=t,






點評:此題轉化為對勾函數求最大值時,關鍵在于求自變量的取值范圍,所以必須充分挖掘三角形的隱含條件,結合正余弦定理及三角形面積公式轉化為一元二次方程,利用三角函數、導數等知識即可求解.此方法思路雖然簡單、自然,但解答過程繁雜,運算量大,不宜提倡.
解法三(坐標法)
如圖不妨令a=6,
以BC連線為x軸,BC的中垂線為y軸建立平面直角坐標系,
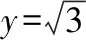
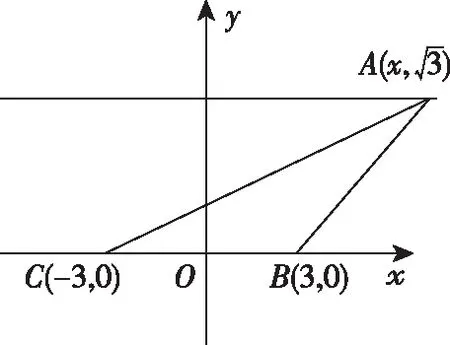



因為b,c>0,
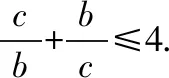
點評:從點的坐標出發,結合兩點間距離公式,原式轉化為函數關系式,變形后利用基本不等式可將問題解決. 經比較發現,選擇B,C為定點,A為動點,以BC連線為x軸,BC的中垂線為y軸建立平面直角坐標系對解題起到方便、快捷的效果.
三、解題后反思
1.絲絲困惑,一一拆解
【困惑1】滿足A=60°的△ABC有幾個?
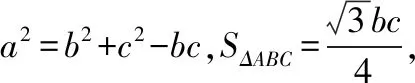
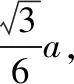





所以像這樣滿足A=60°的三角形ABC存在2個.
【困惑2】如何求解A的取值范圍?
從解法一化簡結果4sin(A+30°)分析可知,
在△ABC中,0° 所以30° 由此,△ABC不存在最小值.經檢查發現,上述情形是錯誤的.原因是△ABC中沒有考慮角A的取值范圍.那么角A的最大角度是多少?如圖,當△ABC為等腰三角形時,D為BC的中點,此時角A最大. 所以B=C=30°,A=120°, 所以0° 筆者細心研究發現,原題與2016年高考數學江蘇卷第14題的已知條件是等價的,所以原題可轉化為:


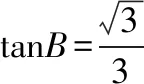
2.等價轉化,尋找最佳解法


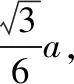
3.小題快做,提高增分意識


