由一個數列問題的教學案例引發的思考

陜西 李 歆

數學是一門思維性很強的學科，在數學教學中，重視學生的思維形成和發展是教師教學的一項根本任務，但是在實際教學中發現，一些教師往往忽視了學生的思維活動.這種情況主要表現在對例題的處理上，教師的思維活動常常占據主導地位，而學生的思維活動只是被動的理解和接受，表面上學生對教學內容是“懂”了，可是這里的“懂”是在教師的思維活動下懂的，學生一旦離開了教師的思維活動，靠自己的思維活動“會不會懂”呢？當得到的回答是否定時，就出現了教學中經常發生的現象——“懂而不會”.這種現象對學生的危害是很大的，當學生的腦海中形成了“懂而不會”的現象，而學生又糊里糊涂的不知道，那么就容易對學生的思維形成“定勢”，從而制約和影響著學生的思維發展.因此，教師在上每一節課前，必須做好精心地準備，對課堂上要講什么，怎么講等問題，要科學、合理地進行設計，尤其在設計學生思維活動時，要讓教師的教學思路與學生的學習思路進行“無縫對接”，以便達到教師講的這種顯性的思維與學生想的這種隱性的思維同步合拍、和諧相融，這樣才能達到有效教學的目的.

一、問題展示

在高三數學復習課中經常會碰到下面一個典型的數列問題：

此題主要考查數列與通項公式的概念，以及由數列的遞推關系式求解數列的通項公式的基本方法.

二、教師的解法

由于例題給出的遞推關系式，超出了常見的幾種基本類型，不能用相應的模式去套用，因此在教學中發現，多數教師在課堂上往往給出以下解法.

得lgan+1=lg3+2lgan,

令bn=lgan,則bn+1=lg3+2bn, ①

整理得bn+1+lg3=2(bn+lg3), ②

這說明數列{bn+lg3}是首項為b1+lg3=lga1+lg3=2lg3,公比為2的等比數列,

所以bn+lg3=2lg3×2n-1, ③

整理得bn=lg32n-1, ④

從而an=32n-1.

通常情況下，教師講完這道題，便認為學生懂了，會進行下一道題.在此試問，學生真的懂了嗎？

三、對幾個細節問題的處理

細節是解決問題的支撐點，決定著解題的成敗.解決一個問題，在某種程度上不是看方法技巧有多么奇妙，而是看對解題細節的處理是否到位，細節處理好了，學生的數學素養也就逐漸培養起來，日積月累就形成能夠獨立解決問題的能力.對于上述的解法1，站在教師的角度看，條理清晰，邏輯嚴密，但是，站在學生的角度看，有三個關鍵細節需要教師在教學時處理到位，否則就會導致學生“懂而不會”現象的形成或者思維障礙的形成.

1.取對數是怎么想到的？

2.①式轉化為②式的核心方法是什么？

3.③式整理為④式隱含了什么數學思想？

將③式整理為④式的過程，其實是一個復雜的過程，既要用到對數的有關公式,又涉及較多的知識點，運算復雜且容易出錯，因此，這一步整理對解法1能否順利得到最后的結果起著舉足輕重的作用，教學中如果對此輕描淡寫地一晃而過，那么對學生數學運算能力的提升將失去一次很好的歷練機會，同時也就失去了解法1的價值.所以，對③式的整理，應該作為重頭戲，教師可啟發并引導學生按照下面兩條途徑完成最后的解法：

一種是先移項，后整理.即先將③式左邊的lg3移到右邊，得bn=2×lg3×2n-1-lg3，再對右邊第一項整理得bn=lg3×2n-lg3，再對右邊整理得bn=lg3×(2n-1)=(2n-1)·lg3=lg32n-1，從而得an=32n-1.

另一種是先代入，后整理.即先將bn=lgan代入③式，得lgan+lg3=2lg3×2n-1，兩邊分別整理得lg3an=lg3×2n，右邊再整理得lg3an=lg32n，所以3an=32n，從而得an=32n-1.

以上兩條途徑雖然出發點不同，但是通過對③式的轉化，都要實現一步極其重要的化歸，就是將(2n-1)lg3化為lg32n-1和將lg3×2n化為lg32n，這里滲透了重要的數學思想——轉化與化歸,對此教師在教學中必須讓學生深刻地理解與領會.

【點評】在數學課堂上，教師講解的例題是非常有限的，只有站在學生思考問題的角度進行解題教學，才能發現影響學生思維的薄弱環節，或者說學生思維容易受阻的“傷痛點”，從而采取有效措施“對癥下藥”，這樣才能讓學生的思維得到提高，使有限的例題教學收到無限的解題效果.

四、回歸課本，探尋第二種解法

對數列的通項公式的教學，課本中一般都是采用列舉的方法，給出數列前面的幾項，通過觀察、歸納與猜想，得到數列的通項公式.如：已知數列{an}的前幾項為1,5,11，19，…，則容易得到該數列的通項公式為an=n2+n-1.面對前面的問題，能不能用課本中介紹的最初求數列的通項公式的方法呢？

【解法2】由已知得，

猜想:an=32n-1.

下面,用數學歸納法證明猜想成立.

(1)當n=1時,猜想顯然成立;

(2)假設當n=k時(k∈N*),猜想成立,即有ak=32k-1,那么，當n=k+1時，

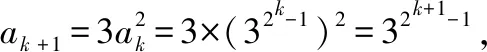
綜合(1)(2)知,對一切n∈N*,猜想都成立.

【點評】前面的問題，雖然沒有用列舉法給出數列前面的幾項，但是根據題目給出的首項和遞推關系式, 一般學生都會很輕松的寫出前面的幾項，同時能順利地觀察到前幾項所展現的一個顯然規律，得到猜想并不難,并且用數學歸納法證明這個猜想也十分簡單,解法1之所以沒有這么做，通常是受思維定勢的影響，被遞推關系式蒙蔽了思維的關注點.對比兩種不同的解法，解法2緊扣課本，知識容量小，思維方法單一，因此更加適合學生.

五、變式與推廣

變式是鞏固解題方法，發現解題規律，提高解題效果的有效途徑.對于前面的問題，教學中可設計下面幾道變式訓練題，讓學生用兩種方法求解并進行比較，以便達到“做一題，學一法，會一類”的效果.

1.變式

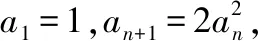
【提示1】按照解法1，可得an=22n-1-1.

猜想:an=22n-1-1.證明略.

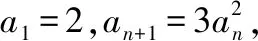
【提示1】按照解法1，可得an=32n-1-1×22n-1.

猜想:an=32n-1-1×22n-1.證明略.

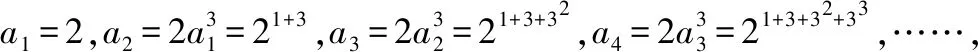
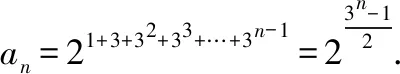
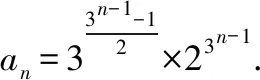
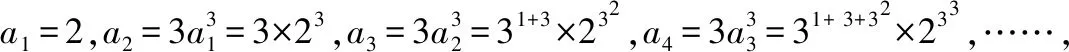
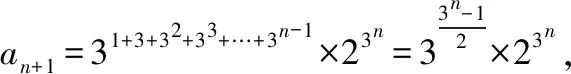
【點評】以上四道變式題的設計，用解法1求解的方法基本上相同，但用解法2求解，因為前幾項的不同變化，所以歸納與猜想的結果也在變化中出現了難易程度，其中,前兩種變式題的歸納與猜想比較容易,但后兩種變式題的歸納與猜想不能急于求成,需要對前幾項的結果中指數中的加法擱置起來,這樣才能便于從中彰顯規律性,為猜想的順利成功奠定基礎.

2.推廣

將以上變式加以推廣,可得到下列一個命題.

【證明】(1)當m=1時,由遞推關系式an+1=qan可知，數列{an}是首項為a1=p，公比為q的等比數列，所以an=pqn-1.

下面用數學歸納法證明猜想成立.

(i)當n=1時，猜想成立；

綜合(i)(ii)可知，猜想對一切n∈N*時都成立.

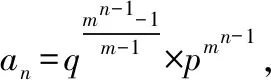
綜合(1)(2)可知，(*)式成立.

【點評】當m=1時，也可以利用歸納與猜想法求解：由已知得a1=p，a2=qa1=q×p，a3=qa2=q2×p，a4=qa3=q3×p，……，猜想：an=qn-1×p=pqn-1，證明略.所以該命題所給出的數列可以看成是等比數列的一個拓展.

六、一點感想

數列是高中數學的重要內容,數列中的一些概念、公式在形成與生成的過程中往往滲透了觀察、歸納、猜想、證明等基本的解題思想和方法,當我們在解決由遞推關系式求數列的通項公式時,應當首先想到這種方法.筆者認為,教師在給出前面的問題后，應該先從熟悉的課本中解決問題的觀念入手，再順應學生的常規思維讓解法2閃亮登場,從而在較短的時間內抓住學生良好的學習熱情,接著再給出四個變式，讓學生用解法2的方法做，這時學生將很快被調動起來,當有些學生對變式3和變式4感到“歸納不出”“猜想很難”時，教師再介紹解法1，并讓學生對兩種不同方法進行比較，這樣學生探究性學習的潛能就會得到激活,由此解決這類數列問題就變得得心應手,相信這樣的課堂教學一定會圓滿而精彩.